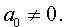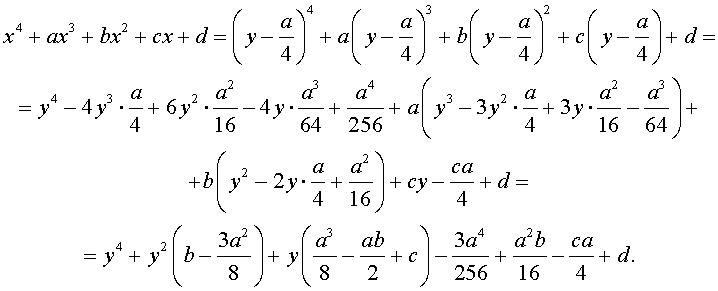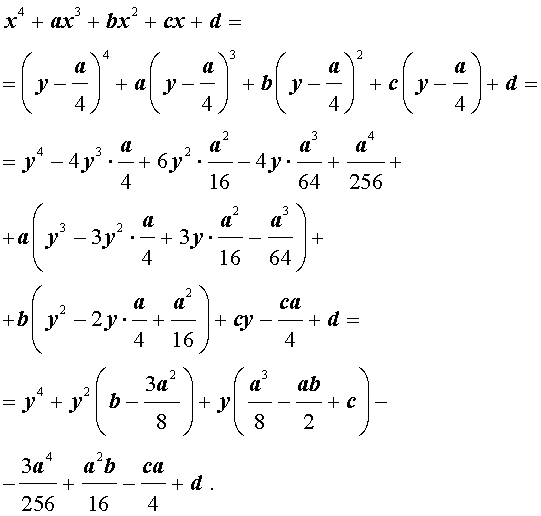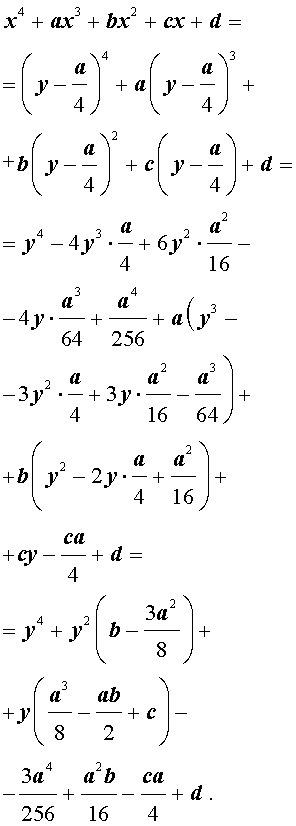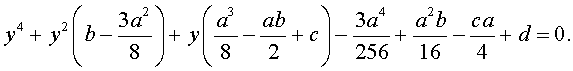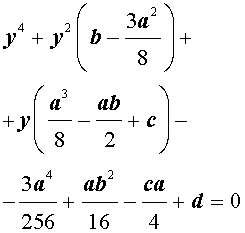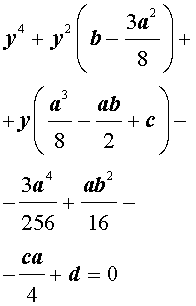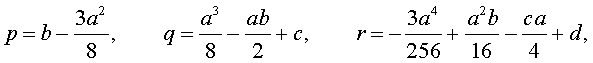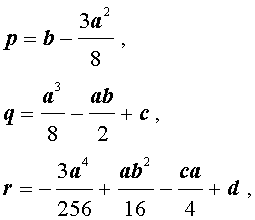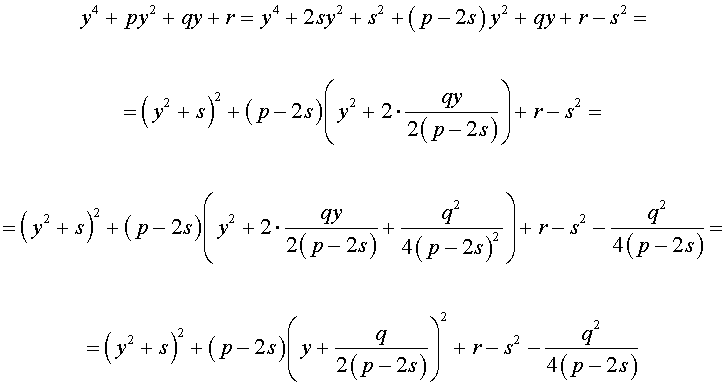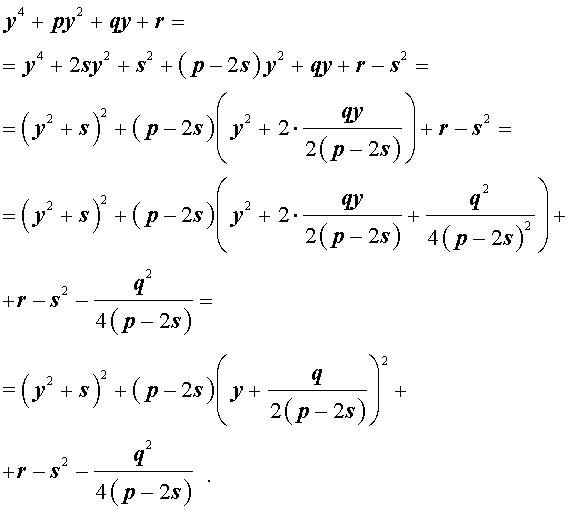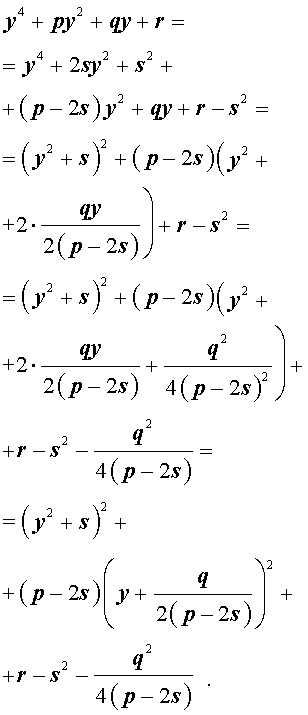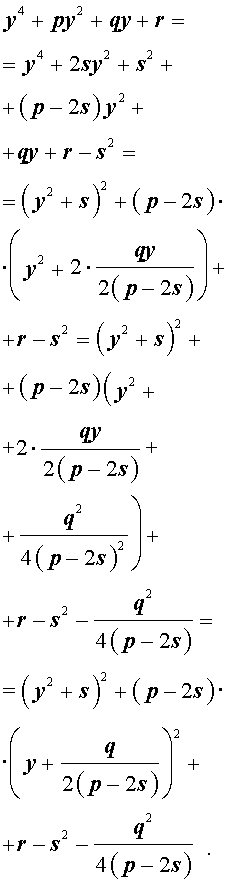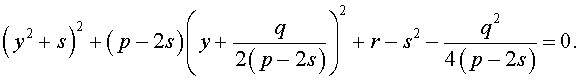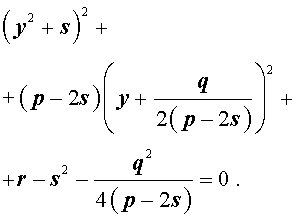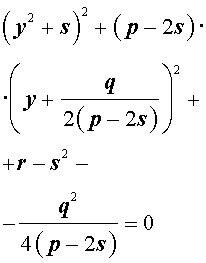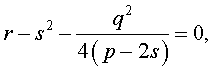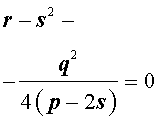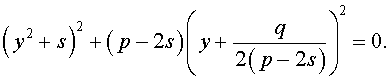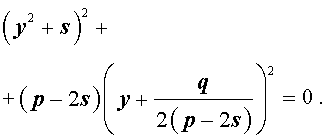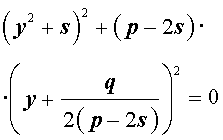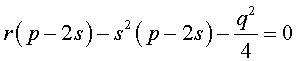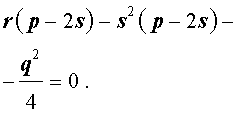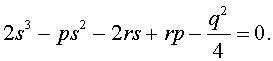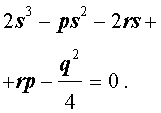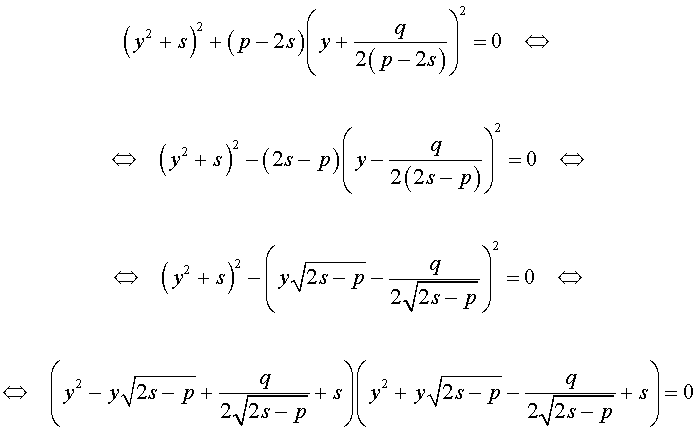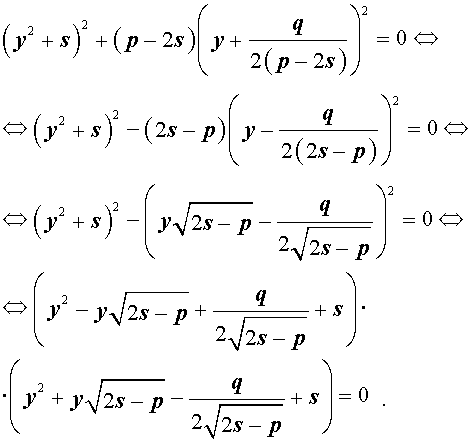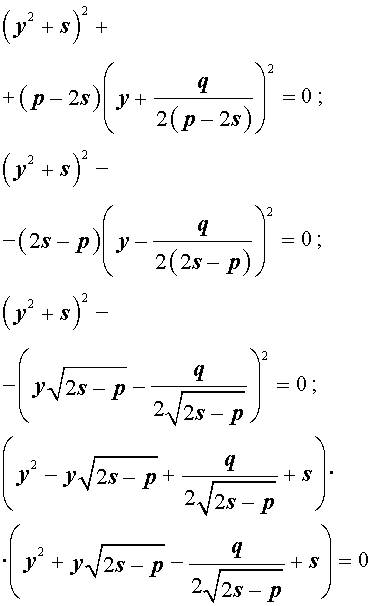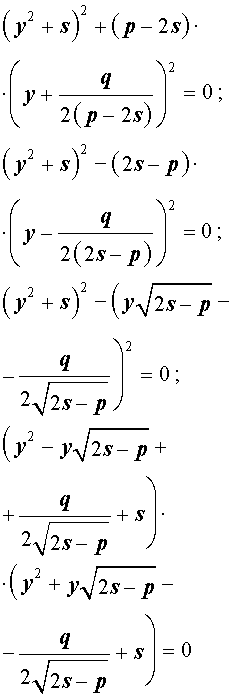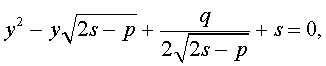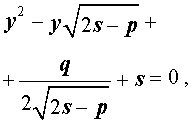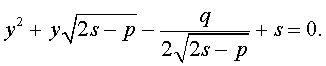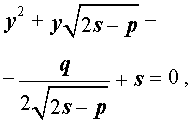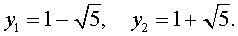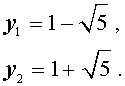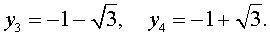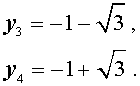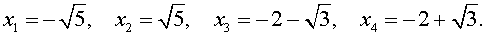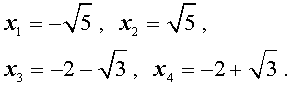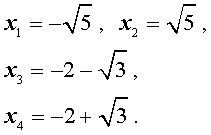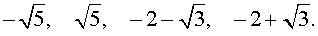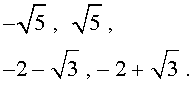Квадратные уравнения, уравнения третьей степени, уравнения четвертой степени – как это все не ново, но только жизнь такая штука, что стоит только покинуть стены родной школы, как все знания также покидают наши головы. Да и решение такого рода уравнений зачастую отнимает слишком много времени, которого в современном ритме жизни и так всегда не хватает.
Наш онлайн калькулятор поможет вам решить любое уравнение, особенно, он поможет тем, для кого ход решения не так важен как правильный ответ. Все что о вас может потребоваться это ввести искомые значения в уравнение и ровно через пару секунд вы получите значение всех неизвестных. Наш онлайн калькулятор это легко, просто и быстро!
Видео:Как решать уравнения четвёртой степени. Формула Феррари | #БотайСоМной #026 | Борис ТрушинСкачать
Решение уравнений 4-ой степени. Метод Феррари
 Схема метода Феррари |
| Приведение уравнений 4-ой степени |
| Разложение на множители. Кубическая резольвента |
| Пример решения уравнения 4-ой степени |
Видео:Решение уравнений четвертой степени (метод Феррари)Скачать
Схема метода Феррари
Целью данного раздела является изложение метода Феррари , с помощью которого можно решать уравнения четвёртой степени
| a0x 4 + a1x 3 + a2x 2 + + a3x + a4 = 0, | (1) |
где a0, a1, a2, a3, a4 – произвольные вещественные числа, причем 
Метод Феррари состоит из двух этапов.
На первом этапе уравнения вида (1) приводятся к уравнениям четвертой степени, у которых отсутствует член с третьей степенью неизвестного.
На втором этапе полученные уравнения решаются при помощи разложения на множители, однако для того, чтобы найти требуемое разложение на множители, приходится решать кубические уравнения.
Видео:Уравнение 4-й степени. Метод ФеррариСкачать
Приведение уравнений 4-ой степени
Разделим уравнение (1) на старший коэффициент a0 . Тогда оно примет вид
| x 4 + ax 3 + bx 2 + + cx + d = 0, | (2) |
где a, b, c, d – произвольные вещественные числа.
Сделаем в уравнении (2) замену
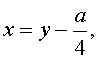 | (3) |
где y – новая переменная.
то уравнение (2) принимает вид
В результате уравнение (2) принимает вид
Если ввести обозначения
то уравнение (4) примет вид
| y 4 + py 2 + qy + r = 0, | (5) |
где p, q, r – вещественные числа.
Первый этап метода Феррари завершён.
Видео:Метод Феррари для решения уравнения 4 степени. Юбилейный выпуск #50.Скачать
Разложение на множители. Кубическая резольвента
Добавив и вычитая в левой части уравнения (5) выражение
где s – некоторое число, которое мы определим чуть позже, из (5) получим
Следовательно, уравнение (5) принимает вид
Если теперь выбрать число s так, чтобы оно являлось каким-нибудь решением уравнения
то уравнение (6) примет вид
Избавляясь от знаменателя, уравнение (7) можно переписать в виде
или, раскрыв скобки, — в виде
Полученное кубическое уравнение (9), эквивалентное уравнению (7), называют кубической резольвентой уравнения 4-ой степени (5).
Если какое-нибудь решение кубической резольвенты (9) найдено, то уравнение (8) можно решить, разложив его левую часть на множители с помощью формулы сокращенного умножения «Разность квадратов».
Таким образом, для решения уравнения (8) остаётся решить квадратное уравнение
а также квадратное уравнение
Вывод метода Феррари завершен.
Видео:4 Метод Феррари решения уравнения четвёртой степениСкачать
Пример решения уравнения 4-ой степени
Пример . Решить уравнение
| x 4 + 4x 3 – 4x 2 – – 20x – 5 = 0. | (12) |
Решение . В соответствии с (3) сделаем в уравнении (12) замену
| x = y – 1. | (13) |
то в результате замены (13) уравнение (12) принимает вид
| y 4 – 10y 2 – 4y + 8 = 0. | (14) |
В соответствии с (5) для коэффициентов уравнения (14) справедливы равенства
| p = – 10, q = – 4, r = 8. | (15) |
В силу (9) и (15) кубической резольвентой для уравнения (14) служит уравнение
которое при сокращении на 2 принимает вид:
| s 3 + 5s 2 – 8s – 42 = 0. | (16) |
| s = – 3. | (17) |
Подставляя значения (15) и (17) в формулу (10), получаем уравнение
Подставляя значения (15) и (17) в формулу (11), получаем уравнение
В завершение, воспользовавшись формулой (13), из (18) и (19) находим корни уравнения (12):
Замечание . При решении примера мы попутно получили разложение левой части уравнения (14) на множители:
| y 4 – 10y 2 – 4y + 8 = = (y 2 – 2y – 4) (y 2 + + 2y – 2). | (20) |
Предоставляем посетителю нашего сайта возможность убедиться в справедливости равенства (19) в качестве несложного упражнения.
Видео:Уравнение четвертой степени (Метод Феррари)Скачать
Калькулятор Уравнений. Решение Уравнений Онлайн
Ввод распознает различные синонимы функций, как asin , arsin , arcsin
Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)
Список математических функций и констант :
• ln(x) — натуральный логарифм
• sh(x) — гиперболический синус
• ch(x) — гиперболический косинус
• th(x) — гиперболический тангенс
• cth(x) — гиперболический котангенс
• sch(x) — гиперболический секанс
• csch(x) — гиперболический косеканс
• arsh(x) — обратный гиперболический синус
• arch(x) — обратный гиперболический косинус
• arth(x) — обратный гиперболический тангенс
• arcth(x) — обратный гиперболический котангенс
• arsch(x) — обратный гиперболический секанс
• arcsch(x) — обратный гиперболический косеканс
📹 Видео
Уравнение четвертой степениСкачать
Решение уравнений четвертой степени. Идея метода ФеррариСкачать
Математика | Кубические уравнения по методу СталлонеСкачать
Уравнение четвертой степени, метод ФеррариСкачать
Решение биквадратных уравнений. 8 класс.Скачать
Уравнения 3 и 4 степени. Методы Кардано и Феррари. ПродолжениеСкачать
Как решать уравнения 4 степени Решите уравнение четвертой степени Разложить на множители Безу столбиСкачать
Решаем быстро и красиво ★ Уравнение четвертой степени ★ x^4+8x-7=0Скачать
9.04.2020_Решение уравнений четвертой степениСкачать
Как решать уравнения с дробью? #shortsСкачать
Математика| СтепениСкачать
Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Как решать уравнения высших степеней, очень лёгкий способ!!!Скачать
Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать
