Онлайн решение найти уравнение высоты треугольника

С помощю этого онлайн калькулятора можно найти высоту треугольника. Для нахождения высоты треугольника введите известные элементы треугольника и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.

Видео:Уравнение прямой и треугольник. Задача про высотуСкачать

Высота треугольника. Определение

Определение 1. Отрезок, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

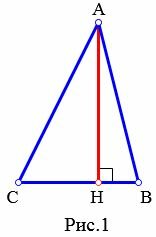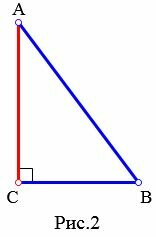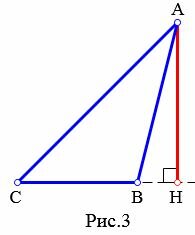Высота треугольника может содержаться внутри треугольника (Рис.1), совпадать со стороной треугольника (при прямоугольном треугольнике высота совпадает с катетом (Рис.2) ), проходить вне треугольника (при тупоугольном треугольнике(Рис.3)).

Видео:найти уравнение высоты треугольникаСкачать

Теорема о пересечении высот треугольника

Теорема 1. Все три высоты треугольника (или их продолжения) пересекаются в одной точке.

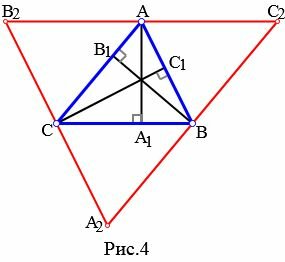Доказательство. Рассмотрим произвольный треугольник ABC (Рис.4). Докажем, что высоты ( small AA_1 ,) ( small BB_1 ,) ( small CC_1 ) пересекаются в одной точке. Из каждой вершины треугольника проведем прямую, параллельно противоположной стороне. Получим треугольник ( small A_2B_2C_2. ) Покажем, что точки ( small A, B, C ) являются серединами сторон треугольника ( small A_2B_2C_2. ) ( small AB=A_2C ) так как они являются противоположными сторонами параллелограмма ( small ABA_2C. ) ( small AB=CB_2 ) так как они являются противоположными сторонами параллелограмма ( small ABCB_2. ) Тогда ( small CB_2=CA_2, ) то есть точка ( small C ) является серединой стороны ( small A_2B_2 ) треугольника ( small A_2B_2C_2. ) Аналогично доказывается, что точки ( small A ) и ( small B ) являются серединами сторон ( small B_2C_2 ) и ( small A_2C_2, ) соответственно.

Далее из ( small AA_1⊥BC ) следует, что ( small AA_1⊥B_2C_2 ) поскольку ( small BC ǁ B_2C_2 ). Аналогично, ( small BB_1⊥A_2C_2, ) ( small CC_1⊥A_2B_2. ) Получили, что ( small AA_1,) ( small BB_1, ) ( small CC_1) являются серединными перпендикулярами сторон ( small B_2C_2, ) ( small A_2C_2, ) ( small A_2B_2, ) соответственно. Но серединные перпендикуляры треугольника пересекаются в одной точке (см. статью Серединные перпендикуляры к сторонам треугольника). Следовательно высоты треугольника или их продолжения пересекаются в одной точке.

Точка пересечения высот треугольника называется ортоцентром.

Видео:Уравнения стороны треугольника и медианыСкачать

Высота треугольника по основанию и площади

Пусть известны сторона треугольника и площадь. Найти высоту треугольника, отпущенная на известную сторону (Рис.5).

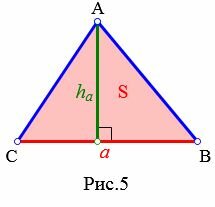Решение. Площадь треугольника по основанию и высоте вычисляется из формулы:

.

.

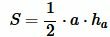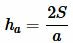(1)

Пример 1. Сторона треугольника равна ( small a=5 ) а площадь ( small S=7. ) Найти высоту треугольника.

Применим формулу (1). Подставляя значения ( small a ) и ( small S ) в (1), получим:

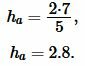Ответ:

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Высота треугольника по трем сторонам

Формула площади треугольника по трем сторонам имеет следующий вид (см. статью на странице Площадь треугольника онлайн):

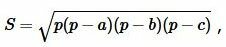(2)

где ( small a, b, c ) стороны треугольника а полупериод ( small p ) вычисляется из формулы:

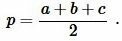(3)

Высота треугольника, отпущенная на сторону ( small a) вычисляется из формулы (1). Подставляя (2) в (1), получим формулу вычисления высоты треугольника по трем сторонам:

.

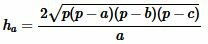(4)

Пример 2. Известны стороны треугольника: ( small a=5, ) ( small b= 4, ) ( small c=7. ) Найти высоту треугольника, отпущенная на сторону ( small a. )

Решение: Найдем, сначала полупериод ( small p ) треугольника из формулы (3):

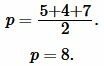Подставляя значения ( small a , b, c ) и ( small p ) в (4), получим:

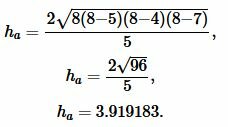Ответ:

Видео:Вычисление медианы, высоты и угла по координатам вершинСкачать

Высота треугольника по двум сторонам и радиусу описанной окружности

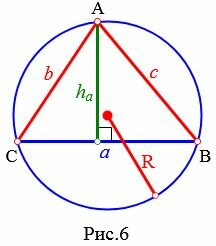Рассмотрим треугольник на рисунке 6. Из теоремы синусов имеем:

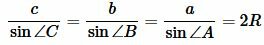(5)

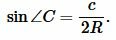(6)

Далее, из теоремы синусов имеем:

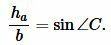(7)

Подставляя (6) в (7), получим:

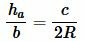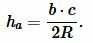(8)

Отметим, что радиус описанной окружности должен удовлетворять следующему неравенству:

Решение: Проверим сначала условие (9):

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Высота треугольника по стороне и прилежащему к ней углу

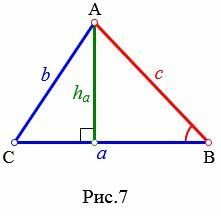Найдем высоту ( small h_a ) треугольника на рисунке 7. Из теоремы синусов имеем:

Пример 4. Известны сторона ( small c=12 ) треугольника и прилежащий угол ( small angle B=30°. ) Найти высоту треугольника, отпущенная на сторону ( small a. )

Решение: Для нахождения высоты треугольника подставим значения ( small c=12 ) и ( small angle B=30° ) в (11). Имеем:

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Решить треугольник Онлайн по координатам

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

A ( ; ), B ( ; ), C ( ; )

Примечание: дробные числа записывайте через точку, а не запятую. Округлять до -го знака после запятой. Видео:Вычисляем высоту через координаты вершин 1Скачать Примеры решений по аналитической геометрии на плоскости В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п. Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать Решения задач о треугольнике онлайн Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти: а) длину стороны $AB$; б) уравнение медианы $BM$; в) $cos$ угла $BCA$; г) уравнение высоты $CD$; д) длину высоты $СD$; е) площадь треугольника $АВС$. Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$. Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти: 1) длину стороны $AB$; 2) внутренний угол $A$ в радианах с точностью до 0,01; 3) уравнение высоты, проведенной через вершину $C$; 4) уравнение медианы, проведенной через вершину $C$; 5) точку пересечения высот треугольника; 6) длину высоты, опущенной из вершины $C$; 7) систему линейных неравенств, определяющую внутреннюю область треугольника. Сделать чертеж. Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$. Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон. Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$. Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, — 4)$, $В(3, 0)$ и $С(0, 6)$. Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$. 📺 Видео SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать Уравнение высоты треугольника (устар.)Скачать 7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать Площадь треугольника. Как найти площадь треугольника?Скачать Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать Даны координаты вершин треугольника АВС.Скачать Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать Задача, которую боятсяСкачать Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать Поделиться или сохранить к себе: Смотрите также Сера — химические свойства, получение, соединения. Нитрат кальция: способы получения и химические свойства Кальций: способы получения и химические свойства Гидроксид натрия: способы получения и химические свойства Гидроксид кальция: способы получения и химические свойства Получение бензола Разница между глюкозой и сахарозой Гидроксид калия: способы получения и химические свойства