Онлайн построение эллиптического параболоида по уравнению (3 видео)

Построение поверхности 3D

Содержание

Результат
Примеры поверхностей
Правила ввода
Поверхности второго порядка. Поверхности вращения.
Эллиптический параболоид, уравнение эллиптического параболоида
уравнение поверхности второго порядка
🎥 Видео

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Результат

Примеры поверхностей

Эллиптический параболоид
Двухсторонний гиперболоид
Мнимый эллипсоид
Две параллельные плоскости
Тригонометрические функции

Указанные выше примеры содержат также:

квадратные корни sqrt(x),
кубические корни cbrt(x)
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
показательные функции и экспоненты exp(x)
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x)
натуральные логарифмы ln(x),
десятичные логарифмы log(x)
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x)
обратные гиперболические функции:
asinh(x), acosh(x), atanh(x), actanh(x)
число Пи pi
комплексное число i

Правила ввода

Можно делать следующие операции

2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5

Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:

Видео:Поверхности второго порядкаСкачать

Поверхности второго порядка. Поверхности вращения.

Поверхность S называется поверхностью вращения вокруг оси OZ, если для любой точки M₀(x₀,y₀,z₀)

этой поверхности окружность, проходящая через эту точку в плоскости z=z₀ с центром в (0,0,z₀) и радиусом

, целиком принадлежит этой поверхности.

Теорема (об уравнении поверхности вращения).

Если в некоторой декартовой прямоугольной системе координат поверхность S задана уравнением

F(x 2 +y 2 ,z)=0, то S — поверхность вращения вокруг оси OZ.

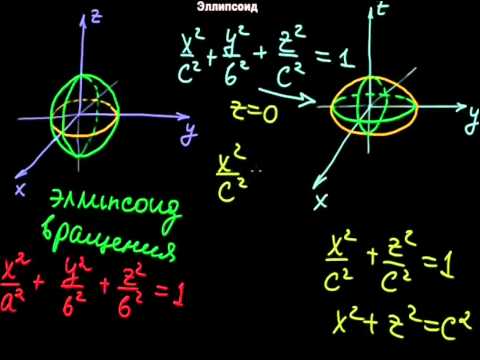
Эллипсоид:

Мнимый эллипсоид.

где a > 0, b > 0, c > 0. Эта поверхность не имеет ни одной вещественной точки.

Свойства эллипсоида.

1. Эллипсоид – ограниченная поверхность, поскольку из его уравнения следует, что

2. Эллипсоид обладает:

центральной симметрией относительно начала координат,

осевой симметрией относительно координатных осей,

плоскостной симметрией относительно начала координат.

3. В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается

Однополостной гиперболоид.

Свойства однополостного гиперболоида.

1. Однополостной гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что

2. Однополостной гиперболоид обладает:

центральной симметрией относительно начала координат,

осевой симметрией относительно всех координатных осей,

плоскостной симметрией относительно всех координатных плоскостей.

3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz, получается

эллипс, а плоскостями, ортогональными осям Ox и Oy – гипербола.

Онлайн построение эллиптического параболоида по уравнению

Двуполостной гиперболоид.

Свойства двуполостного гиперболоида.

1. Двуполостный гиперболоид – неограниченная поверхность, поскольку из его уравнения следует,

что и неограничен сверху.

2. Двуполостный гиперболоид обладает

центральной симметрией относительно начала координат,

осевой симметрией относительно всех координатных осей,

плоскостной симметрией относительно всех координатных плоскостей.

3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz, при

получается эллипс, при – точка, а в сечении плоскостями, перпендикулярными осям

Ox и Oy, – гипербола.

Эллиптический параболоид.

В случае, если a=b≠0, перечисленные выше (эллипсоид, однополостной гиперболоид, двуполостной

гиперболоид, эллиптический параболоид) поверхности являются поверхностями вращения.

Эллиптический параболоид.

Свойства эллиптического параболоида.

1. Эллиптический параболоид – неограниченная поверхность, поскольку из его уравнения следует,

что z ≥ 0 и принимает сколь угодно большие значения.

2. Эллиптический параболоид обладает:

осевой симметрией относительно оси Oz,

плоскостной симметрией относительно координатных осей Oxz и Oyz.

3. В сечении эллиптического параболоида плоскостью, ортогональной оси Oz, получается эллипс, а

плоскостями, ортогональными осям Ox и Oy – парабола.

Уравнение эллиптического параболоида имеет вид:

Если a=b, то эллиптический параболоид представляет собой поверхность вращения, образованную

вращением параболы, параметр которой , вокруг вертикальной оси, проходящей через

вершину и фокус данной параболы.

Пересечение эллиптического параболоида с плоскостью z=z₀>0 является эллипсом.

Пересечение эллиптического параболоида с плоскостью x=x₀ или y=y₀ является параболой.

Видео:Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Эллиптический параболоид, уравнение эллиптического параболоида

Видео:Как строить параболу? | TutorOnlineСкачать

уравнение поверхности второго порядка

Поверхность, представляемая уравнением

при (p > 0, q > 0), носит название эллиптический параболоид.

Сечения плоскостями XOZ и YOZ (главные сечения — это параболы).

Обе параболы обращены вогнутостью в одну сторону (вверх).

Плоскость z=0 касается параболоида в точке O, плоскости z=h при h>0 пересекают эллиптический параболоид подобными между собой эллипсами.

При h XOZ и YOZ и относительно оси OZ. Прямая OZ называется осью эллиптического параболоида. Точка O — его вершиной, величины p и q — параметрами.

При p = q параболы становятся равными, эллипсы обращаются в окружности и параболоид становится поверхностью порождаемой вращением параболы около ее оси (параболоид вращения).

Эллиптический параболоид можно определить как поверхность получаемую равномерным сжатием параболоида вращения к одному из его меридианов.