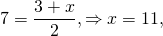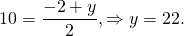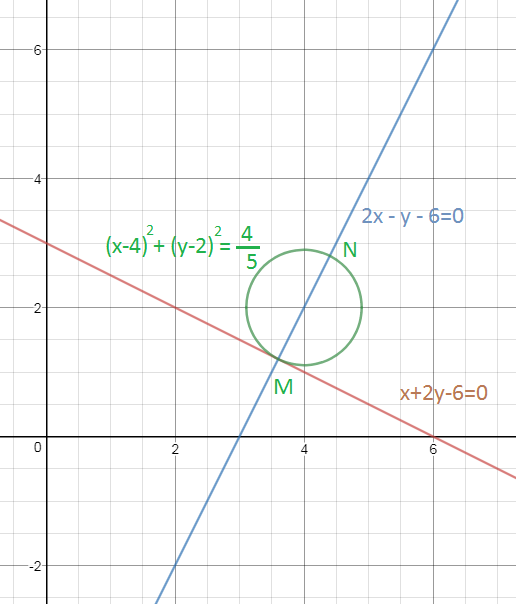Как найти уравнение окружности, симметричной данной?
Симметричные окружности имеют равные радиусы. Следовательно, остаётся найти координаты центра симметричной окружности (как точки, симметричной данной).
1) Окружность задана уравнением (x-3)²+(y+2)²=16. Составить уравнение окружности, симметричной данной относительно точки (7; 10).
Центр окружности (x-3)²+(y+2)²=16 — точка с координатами (3;-2). Найдём точку, симметричную ей относительно точки (7; 10).
Таким образом, центр окружности, симметричной данной, — точка с координатами (11;22). Подставляем в формулу уравнения окружности a=11, b=22, R²=16:
2) Окружность задана уравнением (x+5)²+(y+1)²=9. Составить уравнение окружности, симметричной данной относительно начала координат.
Центром данной окружности является точка (-5;-1). Точка, симметричная данной относительно начала координат — (5;1). Таким образом, для окружности, симметричной данной относительно точки O(0;0) a=5, b=1, R²=9:
3) Окружность задана уравнением (x-7)²+(y-2)²=12. Составить уравнение окружности, симметричной данной относительно прямой y=x.
Центр окружности (x-7)²+(y-2)²=12 — точка (7;2) — при симметрии относительно прямой y=x переходит в точку (2;7). Следовательно, a=2, b=7, R²=12 и искомое уравнение окружности:
4) Окружность задана уравнением (x+4)²+(y-5)²=19. Составить уравнение окружности, симметричной данной относительно прямой y=2x+4.
Центр окружности (x+4)²+(y-5)²=19 — точка (-4;5). Точку, симметричную точке (-4;5) относительно прямой y=2x+4, нашли в прошлый раз — (3,2; 1,4). Таким образом, a=3,2, b=1,4, R²=19 и уравнение симметричной окружности
5) Окружность задана уравнением (x+8)²+(y+3)²=4. Составить уравнение окружности, симметричной данной относительно прямой y= -1.
Центр окружности (x+8)²+(y+3)²=4 — (-8; -3). Точка, симметричная точке (-8; -3) относительно прямой y= -1, имеет такую же абсциссу, x= -8. Расстояние от точки (-8; -3) до прямой y= -1 равно -1-(-3)=2. Расстояние от прямой y= -1 до центра симметричной окружности также равно 2, отсюда -1+2=1 — это ордината центра. Таким образом, точка (-8; 1) — центр окружности, симметричной данной, а R²=4.
Следовательно, искомое уравнение окружности
Видео:6 класс . Фигуры, симметричные относительно прямойСкачать

Окружности симметричны относительно прямой укажите уравнение этой прямой
Уравнение окружности. Правильно ли записал?
1) Запишите уравнение окружности, касающейся осей координат и проходящей через точку (8; -4).
Получилось (x-8)² + (y+4)² = r²
2) Точки A и B симметричны относительно некоторой прямой. Запишите уравнение этой прямой, если A(-2;3)? B(2;1).
Получилось x + y + 0 = 0. В чём ошибка? Решал путём вычитания первого уравнения из второго.
Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Задача 27867 4.2.78) Составить уравнение прямой.
Условие
4.2.78) Составить уравнение прямой, симметричной прямой x+2y-6 = 0 относительно точки А(4; 2).
Решение
1 способ
Прямая, симметричная данной, параллельна данной.
Значит ее уравнение имеет вид
x+2y- d=0
Чтобы найти d подставим координаты точки, принадлежащей этой прямой, например точки Е.
Для этого выберем точку F(2;2), принадлежащую данной прямой и найдем координаты точки Е симметричной относительно А
Е(6;2)
6+2*2-d=0
d=10
2 способ
Составим уравнение прямой, перпендикулярной данной и проходящей через точку А
vector_(данной прямой)=(1;2)
vector_(перпендикулярной прямой)=(2;-1)
Скалярное произведение этих векторов равно 0, векторы ортогональны.
2х-у+с=0
Чтобы найти c подставляем координаты точки А
2*4-2=с
с=-6
2х — у — 6 = 0
Найдем расстояние от точки А до данной прямой
d=|4+2*2-6|/sqrt(1+2^2)=2/sqrt(5)
Составим уравнение окружности с центром в точке А и радиусом R=2/sqrt(5).
Эта окружность касается данной прямой и второй прямой, параллельной данной и находящейся на расстоянии 2/sqrt(5) от точки.
(x-4)^2+(y-2)^2=4/5
(x-4)^2+(2x-6-2)^2=4/5
(x-4)^2=4/25
x-4=2/5 или х-4=-2/5
х=4,4 или х=3,6 — абсцисса точки М
у=2х-6=2*4,4-6=2,8
N(4,4; 2,8)
Прямая, параллельная данной имеет вид
х + 2y — d = 0
Чтобы найти d подставим координаты точки N
4,4+2*2,8 — d=0
О т в е т. х+2y -10 =0 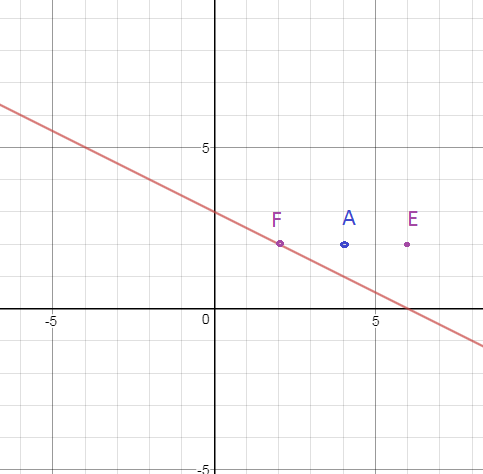
📹 Видео
Уравнение окружности (1)Скачать

Осевая и центральная симметрия, 6 классСкачать

№416. Даны две точки А и В, симметричные относительно некоторой прямой, и точка М.Скачать

Осевая симметрия. 6 класс.Скачать

Симметрия относительно точки. 6 классСкачать

Составляем уравнение прямой по точкамСкачать

Осевая симметрия. Фигуры, симметричные относительно прямой.Скачать

8 класс, 9 урок, Осевая и центральная симметрияСкачать

7й класс; Математика; "Cимметрии относительно точки и симметрии относительно прямой"Скачать

Осевая и центральная симметрии. 6 класс.Скачать

Центральная симметрия. 6 класс.Скачать

6 класс . Симметрия относительно точки .Скачать

УРАВНЕНИЯ ОКРУЖНОСТИ И ПРЯМОЙ 9 класс геометрияСкачать

6 класс. Урок 11. ПРАКТИКА: Симметрия (Часть 1)Скачать

Нахождение точки, симметричной данной относительно плоскости в пространствеСкачать

Уравнение прямой.Скачать

6 класс, 26 урок, СимметрияСкачать