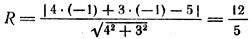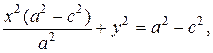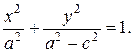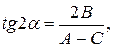Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром.
Если точка С — центр окружности, R — ее радиус, а М — произвольная точка окружности, то по определению окружности
Равенство (1) есть уравнение окружности радиуса R с центром в точке С.
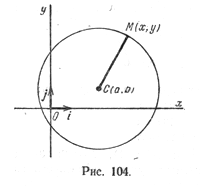
Пусть на плоскости задана прямоугольная декартова система координат (рис. 104) и точка С(а; b) — центр окружности радиуса R. Пусть М(х; у) — произвольная точка этой окружности.
Так как |СМ| = ( sqrt ), то уравнение (1) можно записать так:
(x — a) 2 + (у — b) 2 = R 2 (2)
Уравнение (2) называют общим уравнением окружности или уравнением окружности радиуса R с центром в точке (а; b). Например, уравнение
есть уравнение окружности радиуса R = 5 с центром в точке (1; —3).
Если центр окружности совпадает с началом координат, то уравнение (2) принимает вид
Уравнение (3) называют каноническим уравнением окружности.
Задача 1. Написать уравнение окружности радиуса R = 7 с центром в начале координат.
Непосредственной подстановкой значения радиуса в уравнение (3) получим
Задача 2. Написать уравнение окружности радиуса R = 9 с центром в точке С(3; —6).
Подставив значение координат точки С и значение радиуса в формулу (2), получим
(х — 3) 2 + (у — (—6)) 2 = 81 или (х — 3) 2 + (у + 6) 2 = 81.
Задача 3. Найти центр и радиус окружности
Сравнивая данное уравнение с общим уравнением окружности (2), видим, что а = —3, b = 5, R = 10. Следовательно, С(—3; 5), R = 10.
Задача 4. Доказать, что уравнение
является уравнением окружности. Найти ее центр и радиус.
Преобразуем левую часть данного уравнения:
Это уравнение представляет собой уравнение окружности с центром в точке (—2; 1); радиус окружности равен 3.
Задача 5. Написать уравнение окружности с центром в точке С(—1; —1), касающейся прямой АВ, если A (2; —1), B(— 1; 3).
Напишем уравнение прямой АВ:
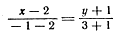
Так как окружность касается данной прямой, то радиус, проведенный в точку касания, перпендикулярен этой прямой. Для отыскания радиуса необходимо найти расстояние от точки С(—1; —1) — центра окружности до прямой 4х + 3y —5 = 0:
Напишем уравнение искомой окружности
Пусть в прямоугольной системе координат дана окружность x 2 + у 2 = R 2 . Рассмотрим ее произвольную точку М(х; у) (рис. 105).
Пусть радиус-вектор OM > точки М образует угол величины t с положительным направлением оси Ох, тогда абсцисса и ордината точки М изменяются в зависимости от t
(0 2 = 3 cos 2 t, у 2 = 3 sin 2 t. Складывая эти равенства почленно, получаем
Видео:Каноническое уравнение окружностиСкачать

Лекция 8. Линии второго порядка.
8.1. Окружность, исследование уравнения окружности.
8.2. Вывод канонического уравнения эллипса.
8.3. Гипербола и парабола, их канонические уравнения.
8.4. Линии второго порядка. Приведение кривых второго порядка к каноническому виду.
8.5. Полярное уравнение кривой второго порядка.
8.1
Окружностьюназывается множество всех точек плоскости, равноудаленных от данной точки (центра окружности) на расстояние, равное радиусу окружности.
Пусть С(а,в) – центр окружности, r – радиус окружности, M(x,y) – произвольная точка окружности (Рисунок 8.1). По определению окружности 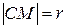
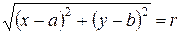
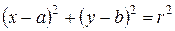
Таким образом, координаты любой точки, лежащей на окружности, удовлетворяют уравнению (8.1). Покажем, что координаты точки, не лежащей на окружности, не удовлетворяют уравнению (8.1).
Действительно, если точка М — внутри окружности, то расстояние 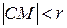
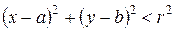
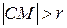
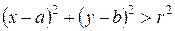
Если в уравнении (8.1) раскрыть скобки, то получим уравнение
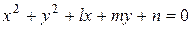
где 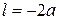
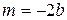
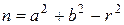
Если 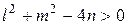
Если 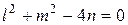
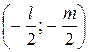
Если 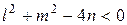
Рисунок 8.2.Окружность, имеющая
Уравнение (8.1) можно упростить, если поместить начало новой системы координат в центр окружности (Рисунок 8.2). Тогда ее уравнение будет иметь вид:
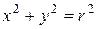
Это уравнение называется каноническим уравнением окружности, т.е. уравнением самого простого вида.
8.2
Эллипсомназывается множество всех точек плоскости, сумма расстояний которых до двух данных точек F1 и F2, называемых фокусами, есть величина постоянная (ее обозначают 2а) и большая, чем расстояние между фокусами.
Середина расстояния между фокусами называется центром эллипса, т.к. относительно этой точки эллипс симметричен.
Длина |F1F2| называется фокусным расстоянием, обозначим ее 2с, а половина этого расстояния называется полуфокусным расстоянием, оно равно с.
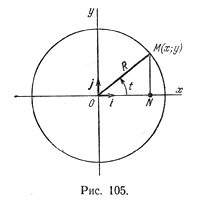
Примем центр эллипса за начало координат, за ось абсцисс примем прямую, проходящую через фокусы (Рисунок 8.3).
Рисунок 8.3. Эллипс
Тогда координаты фокусов будут F1(-c;0), F2(c;0). Всякий отрезок, соединяющий две точки эллипса, если он проходит через центр, называется диаметром эллипса. Наибольший диаметр проходит через фокусы, этот диаметр A1A2 называется большой осью эллипса. Длина большой оси эллипса |A1A2|=2a. Действительно, по определению эллипса |F1A2|+|F2A2|=2a, но |F1A2|=|OA2|+c, |F2A2|=|OA2|-c. Тогда получаем 2|OA2|=2a, или |OA2|=a. Аналогично |A1O|=a, следовательно, |A1A2|=2a. Число а называется большой полуосью. Наименьший диаметр эллипса перпендикулярен наибольшему, его называют малой осью эллипса и обозначают через 2b, так что |B1B2|=2b. Число b называется малой полуосью. Концы осей, т.е. точки A1,A2,B1,B2 называются вершинами эллипса. Основное свойство эллипса применимо и для вершин В1 и В2. Например, для вершины В2 получим |F1B2|+|F2B2|=2a, а т.к. |F1B2|=|F2B2|, то 2|F2B2|=2a, или |F2B2|=a. Тогда из прямоугольного ∆OF2B2 получаем важное соотношение:

Форма эллипса при заданном а зависит только от расстояния между фокусами, т.е. от с. При сближении фокусов и при совпадении их с началом координат эллипс постепенно обратится в окружность. Наоборот, если фокусы отодвигаются от начала координат, эллипс постепенно сплющивается и вырождается в прямолинейный отрезок A1A2. Степень сжатия эллипса определяется его эксцентриситетом, который определяется дробью:
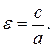
Для эллипса эксцентриситет может изменяться от 0 до 1, причем для окружности 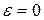

Для получения канонического уравнения эллипса возьмем произвольную точку эллипса М(x,y). Тогда по определению |MF1|+|MF2|=2a. Выразим это равенство в координатах:

Для упрощения уравнения (8.6) придется дважды его возводить в квадрат и приводить подобные члены. В результате будет получено уравнение
или после деления на 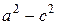
Далее учитывая, что b 2 =a 2 -c 2 , получаем каноническое уравнение эллипса:

Построение эллипса, согласно его определению, можно осуществить посредством нити длиной 2а, закрепленной концами в фокусах. Зацепив нить острием карандаша, и двигая его так, чтобы нить всё время была в натянутом состоянии, мы заставим острие вычертить эллипс.
8.3
Гиперболой называется множество всех точек плоскости, абсолютная величина разности расстояний которых до двух данных точек 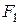
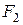
Середина расстояния между фокусами называется центром гиперболы, так как относительно этой точки гипербола симметрична. Длина 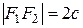
Всякий отрезок, соединяющий две точки гиперболы и проходящий через центр, называется диаметром гиперболы. Наименьший диаметр лежит на оси абсцисс; этот диаметр 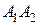
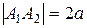

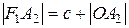
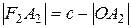
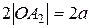
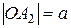
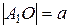
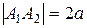
Число 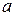
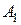
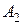
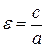
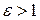
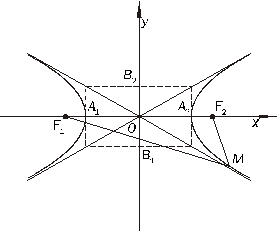
Рисунок 8.4. Гипербола
Пусть 
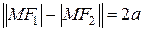
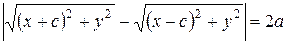
Уравнение (8.8) в результате преобразований, аналогичных проводимым при выводе уравнения эллипса, может быть сведено к виду:
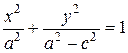
Обозначая 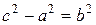
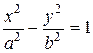
Прямые 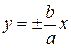
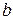
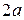
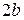
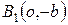
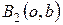
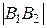
Если в уравнении (8.9) 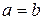

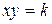
Заметим, что уравнение

тоже определяет гиперболу, у которой действительная ось расположена на оси 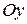
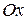
Параболой называется множество всех точек плоскости, равноудаленных от данной точки 
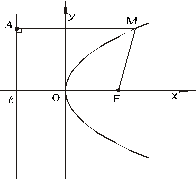
Для вывода канонического уравнения параболы проведем ось 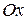

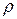
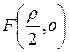
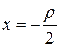

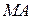
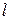
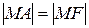
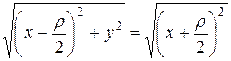
Рисунок 8.5. Парабола.
Возводя в квадрат и приводя подобные, получаем каноническое уравнение параболы:
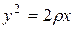
Вершинойпараболы называется точка пересечения параболы с ее осью симметрии. Ось симметрии параболы называется осью параболы. Парабола, определяемая уравнением (8.11), имеет ось, совпадающую с осью 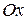
Заметим, что уравнение 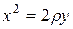
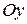
8.4
Между эллипсом, гиперболой и параболой имеется близкое родство. Это объясняется тем, что все они — линии второго порядка. Все эти линии могут быть получены при пересечении прямого кругового конуса с плоскостью, поворачивающейся вокруг оси, выбранной, например, перпендикулярно к оси конуса (Рисунок 8.6). Пока наклон мал, в сечении получается эллипс. При увеличении наклона эллипс удлиняется, его эксцентриситет растет. Когда плоскость наклонена к оси конуса так же, как образующие, в сечении получается парабола. Наконец, когда плоскость будет пересекать обе половины конуса, в сечении будет гипербола. По этой причине эллипс, гиперболу и параболу иногда называют коническими сечениями.
Рисунок 8.6. Родство кривых второго порядка.
Родство между указанными линиями обусловлено тем, что все они задаются уравнением второй степени, а поэтому и носят общее название линий(или кривых) второго порядка.
Общим уравнением линий второго порядканазывается уравнение вида
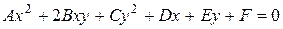
Путем преобразования координат это уравнение можно привести к каноническому виду. Осуществим поворот осей координат на угол 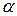
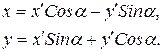
Угол 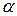
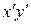
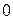
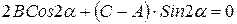
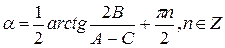
Формула (8.15) определяет 4 возможных значения для 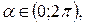
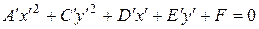
Если 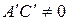

которое с помощью параллельного переноса начала координат
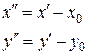
сводится к каноническому виду.
Если 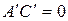

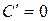
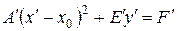
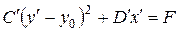
Применяя параллельный перенос (8.18), где 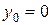
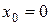
Заметим, что при любом повороте осей координат (8.13), хотя координаты 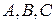
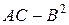
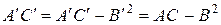
1. Если 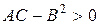
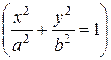
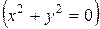
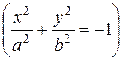
2. Если 
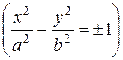
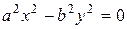
3. Если 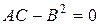
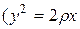
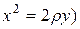
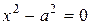
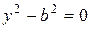
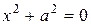
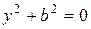
8.5
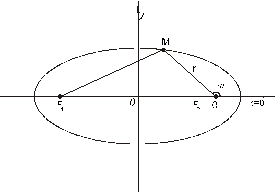
Выведем полярное уравнение линии второго порядка на примере эллипса.
Рисунок 8.7. Полярное уравнение эллипса
Поместим полюс 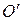
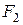

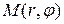
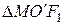

Учитывая, что 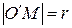
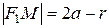
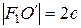

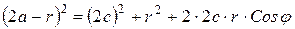
Откуда, заменяя 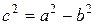
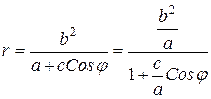
Обозначим 
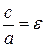
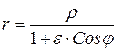
полярное уравнение эллипса.
Если поместить полюс в левый фокус эллипса, то полярное уравнение будет иметь вид
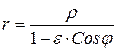
Заметим, что уравнения (8.21) и (8.22) являются полярными уравнениями любой кривой второго порядка, его вид определяется величиной эксцентриситета. Если 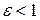
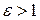
Дата добавления: 2015-08-21 ; просмотров: 2217 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

ОБЩЕЕ УРАВНЕНИЕ ЛИНИЙ ВТОРОГО ПОРЯДКА
Линии второго порядка
1. Основные понятия.
6. Общее уравнение линий второго порядка.
ОСНОВНЫЕ ПОНЯТИЯ
Рассмотрим линии, определяемые уравнениями второй степени относительно текущих координат

Коэффициенты уравнения – действительные числа, но, по крайней мере, одно из чисел 
ОКРУЖНОСТЬ
Простейшей кривой второго порядка является окружность.
Определение. Окружностью радиуса R с центром в точке 


Каноническое уравнение окружности 
Эллипс
Определение. Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная и большая, чем расстояние между фокусами.
Каноническое уравнение эллипса 

с – половина расстояния между фокусами; a – большая полуось; b – малая полуось.



Теорема. Фокусное расстояние и полуоси эллипса связаны соотношением:
Определение.Характеристикой эллипса, показывающей меру его вытянутости, является эксцентриситет – величина, определяемая отношением: 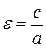
Замечание. Для эллипса 
Определение.Прямые 
Теорема. Если 
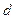


Замечание. Если a = b, то c = 0, а значит, фокусы сливаются, и эллипс превращается в окружность.
Если же 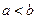



Пример. Составьте уравнение эллипса, если его фокусы F1(0; 0), F2(1; 1), а большая ось равна 2.
Уравнение эллипса имеет вид: 
Расстояние между фокусами: 2c = 
a 2 – b 2 = c 2 = 
По условию большая ось равна 2, то есть 2а = 2, откуда получаем, что
а = 1, b = 
Тогда искомое уравнение эллипса имеет вид: 
Гипербола
Определение. Гиперболойназывается линия, для всех точек которой модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы 

Теорема. Фокусное расстояние и полуоси гиперболы связаны соотношением:
Ось 2а называется действительной осью гиперболы.
Ось 2b называется мнимой осью гиперболы.
Прямоугольник со сторонами 2а и2b называется основным прямоугольником гиперболы.
Гипербола имеет две асимптоты, уравнения которых
Замечание.Для гиперболы эксцентриситет 
Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/ε от него, называются директрисами гиперболы. Их уравнения: 
Определение. Гипербола называется равносторонней, если ее полуоси равны ( 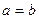
Ее каноническое уравнение 
Определение. Эксцентриситетом гиперболы называется отношение расстояние между фокусами к величине действительной оси гиперболы, обозначается 

Кривая, определяемая уравнением 



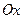
Гиперболы 

Пример. Составьте уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса, заданного уравнением
Найдем фокусное расстояние для эллипса:
Тогда искомое уравнение гиперболы 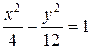
Парабола
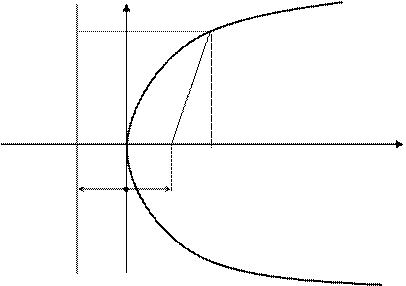
Определение. Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.
Каноническое уравнение параболы y 2 = 2px .
💡 Видео
Уравнение окружности (1)Скачать

Видеоурок "Гипербола"Скачать

9 класс, 6 урок, Уравнение окружностиСкачать

Вывод уравнения окружностиСкачать

ЭллипсСкачать

§18 Каноническое уравнение эллипсаСкачать

начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

§2 Различные уравнения окружностиСкачать

Видеоурок "Канонические уравнения прямой"Скачать

Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Аналитическая геометрия: окружность и эллипсСкачать
Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

Видеоурок "Окружность"Скачать

9 класс, 7 урок, Уравнение прямойСкачать

§24 Каноническое уравнение параболыСкачать

Лекция 14, 2021. Вывод уравнения эллипса и гиперболыСкачать

11 класс, 52 урок, ЭллипсСкачать