Ограниченное решение дифференциального уравнения это (5 видео)

Содержание

Ограниченные решения некоторых обыкновенных дифференциальных уравнений в банаховом пространстве Текст научной статьи по специальности « Математика»
Аннотация научной статьи по математике, автор научной работы — Байзаев Саттор, Мухамадиев Эргашбой
Похожие темы научных работ по математике , автор научной работы — Байзаев Саттор, Мухамадиев Эргашбой
Bounded solutions of ordinary differential equations in Banah space
Текст научной работы на тему «Ограниченные решения некоторых обыкновенных дифференциальных уравнений в банаховом пространстве»
Особые решения дифференциальных уравнений
Методические рекомендации для преподавателей математики и студентов средних специальных учебных заведений по теме «Дифференциальные уравнения»
🔥 Видео

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Ограниченные решения некоторых обыкновенных дифференциальных уравнений в банаховом пространстве Текст научной статьи по специальности « Математика»

Видео:Частное решение дифференциального уравнения. 11 класс.Скачать

Аннотация научной статьи по математике, автор научной работы — Байзаев Саттор, Мухамадиев Эргашбой

В этой статье рассматривается проблема ограниченных решений на оси обычных дифференциальных уравнений с постоянными коэффициентами в банаховом пространстве. Найдены необходимые и достаточные условия существования и единство названных решений. На основе решения различных типов уравнений авторы изучили теоремы, аннотации и нашли доказательства решений для уравнения гиперболы.

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Bounded solutions of ordinary differential equations in Banah space

In this article is considered the problem of bounded solutions on the axis of ordinary differential equations with constant coefficients in Banah space. The necessary and successful conditions of existence and unity of the pointed solutions is found. The authors on the ground of solution of different types of equations they worked out theorems, lemmas and proofs of hyperbola equation solutions. In paper are considered the problem of bounded solutions on the axis of ordinary differential equations with constant coefficients in Banah space. The necessary and successful conditions of existence and unicnis pointed solutions are founded.

Видео:Общее и частное решение дифференциального уравненияСкачать

Текст научной работы на тему «Ограниченные решения некоторых обыкновенных дифференциальных уравнений в банаховом пространстве»

д.ф.м.н., профессор ТГУПБП, Мухамадиев Эргашбой,-д.ф.м.н., профессор Вологодского технического университета (РФ)

ОГРАНИЧЕННЫЕ РЕШЕНИЯ НЕКОТОРЫХ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В БАНАХОВОМ ПРОСТРАНСТВЕ

Пусть В — банахово пространство, А:В ^ В — линейный ограниченный оператор и ^(/), t е Я — ограниченная непрерывная

функция со значением в пространстве В.

Рассмотрим обыкновенное дифференциальное уравнение

Предположим, что спектр 0>.

В дальнейшем мы будем использовать нижеследующую теорему о представлении ограниченных на всей прямой решений линейного дифференциального уравнения (1) (см., напр., [1]).

Теорема. Для того чтобы уравнение (1) для всех непрерывных и ограниченных на всей оси (—да;+да) вектор-функций g(t) имело ограниченное на всей оси решение, необходимо и достаточно, чтобы спектр 0,

|е Л-‘)g(если Яел 0. Тогда подставляя в последнюю формулу g (7) = / (7, х), в развернутом виде имеем

т. е. интеграл от абстрактной функции е _Л(/-5) g (7) по интервалу (-ад; 7) совпадает с обычным несобственным интегралом по 5 на отрезке (-ад; 7) от функции /(5, х) при фиксированном х . Если уравнение (3) переписать в виде

с правой частью, зависящей от параметра х, то рассмотрение общего решения показывает, что ограниченное по ; решение уравнения (5) представляется формулой (4), при этом достаточно ограниченность функции /(7, х) по ; при каждом х .

Следующий пример уравнения (1) — это интегро-дифференциальные уравнения

&0>У) + Ьг(7, у) + а | е

*(у-л)2(7, = /(7, у), яе а > 0,

а(у-л) 1(7, = /(7, у), Яе а 0,

Ьу(у) — d | е а(у—л)Яе а Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

При условии (11) спектр 0, если ЯеЬ 0, если ЯеЬ > 0.

Доказательство. Так как

Это неравенство эквивалентно (11). Так как точка Ь лежит на окружности Б, то Б с 0>, если ЯеЬ > 0 и Б с <Л:Яеа(Л) Надоели баннеры? Вы всегда можете отключить рекламу.

Видео:Решение дифференциальных уравнений ДИФФУРЫСкачать

Особые решения дифференциальных уравнений

Решение дифференциального уравнения

называется особым , если в каждой его точке нарушается свойство единственности, т. е. если через каждую его точку кроме этого решения проходит и другое решение, имеющее в точке ту же касательную, что и решение , но не совпадающее с ним в сколь угодно малой окрестности . График особого решения будем называть особой интегральной кривой уравнения (1). Если функция и ее частные производные и непрерывны по всем аргументам , то любое особое решение уравнения (1) удовлетворяет также уравнению

Значит, чтобы отыскать особые решения (1), надо исключить из уравнений (1) и (2).

Полученное после исключения из (1) и (2) уравнение

Часто бывает так, что распадается на несколько ветвей . Тогда нужно установить, является ли каждая в отдельности ветвь решением уравнения (1), и если является, то будет ли оно особым решением, т.е. нарушается ли единственность в каждой его точке.

Пример 1. Найти особые решения дифференциального уравнения

а) Находим p-дискриминантную кривую. В данном случае и условие (2) принимает вид , отсюда . Подставляя это выражение для в уравнение (4), получаем

Кривая (5) есть p-дискриминантная кривая уравнения (4): она состоит из одной ветви — параболы.

б) Проверяем, является ли p-дискриминантная кривая решением заданного уравнения. Подставляя (5) и ее производную в (4), убеждаемся, что есть решение уравнения (4).

в) Проверяем, является ли решение (S) особым решением уравнения (4). Для этого найдем общее решение уравнения (4). Перепишем (4) в виде . Это уравнение Клеро. Его общее решение

Выпишем условие касания двух кривых и в точке с абсциссой :

Первое равенство выражает совпадение ординат кривых, а второе выражает совпадение угловых коэффициентов касательных к этим кривым в точке с абсциссой .

Полагая , находим, что условия (7) принимают вид

Подставляя в первое из равенств (8), получаем или т.е. при первое равенство выполняется тождественно, так как есть абсцисса произвольной точки.

Итак, в каждой точке кривой (5) ее касается некоторая другая кривая семейства (6), а именно та, для которой . Значит, есть особое решение уравнения (4).

г) Геометрическое истолкование.
Общее решение уравнения (4) есть семейство прямых (6), а особое решение (5) является огибающей этого семейства прямых (рис. 19).

Огибающей семейства кривых

называется такая кривая, которая в каждой своей точке касается некоторой кривой семейства (9) и каждого отрезка которой касается бесконечное множество кривых из (9). Будем говорить, что кривые и касаются в точке , если они имеют в этой точке общую касательную.

Если (9) есть общий интеграл уравнения (1), то огибающая семейства кривых (9), если она существует, будет особой интегральной кривой этого уравнения. В самом деле, в точках огибающей значения совпадают со значениями для интегральной кривой, касающейся огибающей в точке , и, следовательно, в каждой точке огибающей значения удовлетворяют уравнению , т.е. огибающая является интегральной кривой.

Далее, в каждой точке огибающей нарушена единственность, так как через точки огибающей по одному направлению проходит, по крайней мере, две интегральные кривые: сама огибающая и касающаяся ее в рассматриваемой точке интегральная кривая семейства (9). Следовательно, огибающая является особой интегральной кривой.

Из курса математического анализа известно, что огибающая входит в состав C-дискриминантной кривой (коротко СДК), определяемой системой уравнений

Некоторая ветвь СДК заведомо будет огибающей, если на ней:

1) существуют ограниченные по модулю частные производные

где и — постоянные;

Замечание. Условия 1) и 2) лишь достаточны, а потому ветви СДК, на которых нарушено одно из этих условий, тоже могут быть огибающими.

Пример 2. Найти особые решения дифференциального уравнения

а) Находим C-дискриминантную кривую. Имеем , так что отсюда . Подставляя это значение в (14), получаем откуда

Это и есть C-дискриминантная кривая: она состоит из двух прямых и .

б) Непосредственной подстановкой убеждаемся, что каждая из ветвей СДК является решением уравнения (13).

в) Докажем, что каждое из решений (15) является особым решением уравнения (13). В самом деле, так как и , то на каждой ветви СДК имеем (предполагаем, что решение уравнения (13) рассматривается на отрезке

где — область допустимых значений .

Заметим, что на любой из ветвей СДК в области 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQCAMAAABncAyDAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAMRDQiiHowAFBoWFRoLFx3eb7ogAAAMZJREFUKM+1UksSwyAIVUHAX+T+p602mTYkdqZd1AUL5fk+4NzfjiQvv/QXwkz++/6kyblOYfXmMd4vNxglaF//xu0KEeJZdVYXkDFUbhaSDCDqDtDhO3ASgOypGJbMyVh4A3A8bBpQq1URM1exAEcTUHaF4R5ZzFQXDE+FuDIfET4AiqZFe+PykiQHYIbb8rAgTsAM3lvTjvc5DCVeORANFjSxbhfOqn6ux5wPICRojOf2fJ81Uscj+bmEUc5q4jKCXucmPQAaYQaRCPmIUQAAAABJRU5ErkJggg==» />, так дх что выполняется одно из условий (12). Значит, условия (11) и (12) выполняются, а, следовательно, прямые (15) являются огибающими парабол (14).

Итак, установлено, что каждое из решений (15) есть особое решение.

В вопросах отыскания особых решений оказываются полезными следующие символические схемы:

Схема (16) означает, что уравнение p-дискриминантной кривой может распадаться на три уравнения:

1) — уравнение огибающей;

2) — уравнение геометрического места точек заострения (возврата);

3) — уравнение геометрического места точек прикосновения интегральных линий, причем множитель входит в в квадрате.

Схема (17) означает, что уравнение C-дискриминантной кривой может распадаться на три уравнения:

1) — уравнение огибающей;

2) — уравнение геометрического места узловых точек, причем множитель входит в в квадрате;

3) — уравнение геометрического места точек заострения, причем множитель входит в в кубе.

Не обязательно, чтобы для каждой задачи все составные части и фигурировали в соотношениях (16) и (17).

Из всех геометрических мест только огибающая есть особое решение дифференциального уравнения. Отыскание огибающей упрощается тем, что в схемы (16) и (17) она входит в первой степени.

В отношении других геометрических мест (точек заострения, узловых точек и точек прикосновения) требуется дополнительный анализ в каждом конкретном случае. То обстоятельство, что некоторый множитель входит в в квадрате (и совсем не входит в ) указывает на то, что здесь может быть геометрическое место точек прикосновения интегральных линий. Аналогично, если некоторый множитель входит в в квадрате (и совсем не входит в ), то здесь может быть геометрическое место узловых точек. Наконец, если множитель входит в в первой степени, а в — в третьей, то возможно наличие геометрического места точек заострения.

Пример 3. Найти особое решение дифференциального уравнения

Решение. Особое решение, если оно существует, определяется системой

где второе уравнение (19) получено из (18) дифференцированием его по . Исключив , получим p-дискриминантную кривую , которая распадается на две ветви

Подстановкой убеждаемся, что обе функции являются решениями уравнения (18).

Чтобы установить, являются ли решения (20) и (21) особыми или нет, найдем огибающую семейства

являющегося общим интегралом для (18).

Выпишем систему для определения C-дискриминантной кривой откуда, исключая , получаем , или и , что совпадает с (20) и (21). В силу того, что на линиях (20) и (21) условия (11) и (12) выполняются, заключаем, что линии и являются огибающими, а значит (20) и (21) есть особые решения заданного уравнения.

Интегральные кривые (22) суть параболы , а линии — огибающие этого семейства парабол (рис. 20).

Пример 4. Найти особые решения дифференциального уравнения

Решение. Дифференцируем (23) по

Исключая из (23) и (24), получим . Дискриминантная кривая есть ось ординат. Она не является интегральной кривой уравнения (23), но согласно схеме (16) может быть геометрическим местом точек прикосновения интегральных кривых.

Решениями уравнения (23) являются параболы и те гладкие кривые, которые можно составить из их частей (рис. 21).

Из чертежа видно, что прямая действительно есть геометрическое место точек прикосновения интегральных кривых уравнения (23).

Пример 5. Найти особые решения дифференциального уравнения

Решение. Найдем . Исключая из системы уравнений получаем

Преобразовав уравнение (25) к виду , находим его общий интеграл .

Найдем . Исключая из системы уравнений будем иметь

Итак, из (26) и (27) имеем

Множитель входит в p-дискриминант и в C-дискриминант в первой степени и дает огибающую, т. е. функция есть особое решение дифференциального уравнения (25). Непосредственной подстановкой убеждаемся, что действительно удовлетворяет уравнению.

Уравнение , входящее во второй степени в p-дискриминант и совсем не входящее в C-дискриминант, дает место точек прикосновения .

Наконец, уравнение , входящее в C-дискриминант во второй степени и совсем не входящее в p-дискриминант, дает место узловых точек (рис.22).

Пример 6. Найти особые решения дифференциального уравнения

а) Ищем p-дискриминантную кривую. Дифференцируя (28) по , получаем , откуда

Подставляя (29) в (28), найдем уравнение :

б) Ищем общий интеграл уравнения (28). Обозначив у’ через р, перепишем (28) в виде

Дифференцируя обе части (28) по и учитывая, что , будем иметь

Приравнивая нулю первый множитель , получаем (29), а соотношение дает

Исключая параметр из уравнений (31) и (32), найдем общее решение уравнения (28):

в) Находим C-дискриминантную кривую. Дифференцируя (33) по C, будем иметь

Подставляя (34) в (33), получаем уравнение .

Согласно символическим схемам (16) и (17) заключаем, что есть огибающая семейства полукубических парабол (33), а есть геометрическое место точек заострения (множитель входит в уравнение в кубе) (рис. 23). Подстановкой в уравнение (28) убеждаемся, что есть решение, а решением не является (при уравнение (28) не имеет смысла). Таким образом, решение есть особое (огибающая семейства интегральных линий).

Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Методические рекомендации для преподавателей математики и студентов средних специальных учебных заведений по теме «Дифференциальные уравнения»

Разделы: Математика

I. Обыкновенные дифференциальные уравнения

1.1. Основные понятия и определения

Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную x, искомую функцию y и её производные или дифференциалы.

Символически дифференциальное уравнение записывается так:

Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.

Решением дифференциального уравнения называется такая функция , которая обращает это уравнение в тождество.

Порядком дифференциального уравнения называется порядок старшей производной, входящей в это уравнение

1. Рассмотрим дифференциальное уравнение первого порядка

Решением этого уравнения является функция y = 5 ln x. Действительно, , подставляя y’ в уравнение, получим – тождество.

А это и значит, что функция y = 5 ln x– есть решение этого дифференциального уравнения.

2. Рассмотрим дифференциальное уравнение второго порядка y» — 5y’ +6y = 0. Функция – решение этого уравнения.

Действительно, .

Подставляя эти выражения в уравнение, получим: , – тождество.

А это и значит, что функция – есть решение этого дифференциального уравнения.

Интегрированием дифференциальных уравнений называется процесс нахождения решений дифференциальных уравнений.

Общим решением дифференциального уравнения называется функция вида ,в которую входит столько независимых произвольных постоянных, каков порядок уравнения.

Частным решением дифференциального уравнения называется решение, полученное из общего решения при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находится при определённых начальных значениях аргумента и функции.

График частного решения дифференциального уравнения называется интегральной кривой.

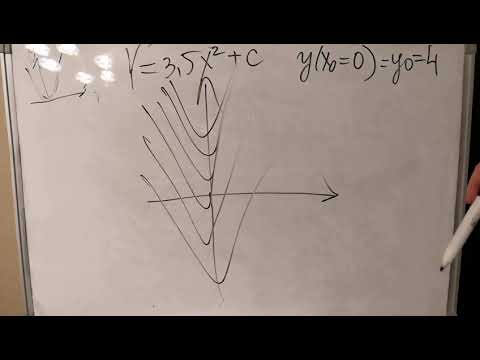
1.Найти частное решение дифференциального уравнения первого порядка

xdx + ydy = 0, если y = 4 при x = 3.

Решение. Интегрируя обе части уравнения, получим

Замечание. Произвольную постоянную С, полученную в результате интегрирования, можно представлять в любой форме, удобной для дальнейших преобразований. В данном случае, с учётом канонического уравнения окружности произвольную постоянную С удобно представить в виде .

— общее решение дифференциального уравнения.

Частное решение уравнения, удовлетворяющее начальным условиям y = 4 при x = 3 находится из общего подстановкой начальных условий в общее решение: 3 2 + 4 2 = C 2 ; C=5.

Подставляя С=5 в общее решение, получим x 2 +y 2 = 5 2 .

Это есть частное решение дифференциального уравнения, полученное из общего решения при заданных начальных условиях.

2. Найти общее решение дифференциального уравнения

Решением этого уравнения является всякая функция вида , где С – произвольная постоянная. Действительно, подставляя в уравнения , получим: , .

Следовательно, данное дифференциальное уравнение имеет бесконечное множество решений, так как при различных значениях постоянной С равенство определяет различные решения уравнения .

Например, непосредственной подстановкой можно убедиться, что функции являются решениями уравнения .

Задача, в которой требуется найти частное решение уравнения y’ = f(x,y) удовлетворяющее начальному условию y(x₀) = y₀, называется задачей Коши.

Решение уравнения y’ = f(x,y), удовлетворяющее начальному условию, y(x₀) = y₀, называется решением задачи Коши.

Решение задачи Коши имеет простой геометрический смысл. Действительно, согласно данным определениям, решить задачу Коши y’ = f(x,y) при условии y(x₀) = y₀,, означает найти интегральную кривую уравнения y’ = f(x,y) которая проходит через заданную точку M₀(x₀,y₀).

II. Дифференциальные уравнения первого порядка

2.1. Основные понятия

Дифференциальным уравнением первого порядка называется уравнение вида F(x,y,y’) = 0.

В дифференциальное уравнение первого порядка входит первая производная и не входят производные более высокого порядка.

Уравнение y’ = f(x,y) называется уравнением первого порядка, разрешённым относительно производной.

Общим решением дифференциального уравнения первого порядка называется функция вида , которая содержит одну произвольную постоянную.

Пример. Рассмотрим дифференциальное уравнение первого порядка .

Решением этого уравнения является функция .

Действительно, заменив в данном уравнении, его значением, получим

то есть 3x=3x

Следовательно, функция является общим решением уравнения при любом постоянном С.

Найти частное решение данного уравнения, удовлетворяющее начальному условию y(1)=1 Подставляя начальные условия x = 1, y =1 в общее решение уравнения , получим откуда C = 0.

Таким образом, частное решение получим из общего подставив в это уравнение, полученное значение C = 0 – частное решение.

2.2. Дифференциальные уравнения с разделяющимися переменными

Дифференциальным уравнением с разделяющимися переменными называется уравнение вида: y’=f(x)g(y) или через дифференциалы , где f(x) и g(y)– заданные функции.

Для тех y, для которых , уравнение y’=f(x)g(y) равносильно уравнению, в котором переменная y присутствует лишь в левой части, а переменная x- лишь в правой части. Говорят, «в уравнении y’=f(x)g(y разделим переменные».

Уравнение вида называется уравнением с разделёнными переменными.

Проинтегрировав обе части уравнения по x, получим G(y) = F(x) + C– общее решение уравнения, где G(y) и F(x) – некоторые первообразные соответственно функций и f(x), C произвольная постоянная.

Алгоритм решения дифференциального уравнения первого порядка с разделяющимися переменными

Производную функции переписать через её дифференциалы
Разделить переменные.
Проинтегрировать обе части равенства, найти общее решение.
Если заданы начальные условия, найти частное решение.

Решить уравнение y’ = xy

Решение. Производную функции y’ заменим на

разделим переменные

проинтегрируем обе части равенства:

Ответ:

Найти частное решение уравнения

Это—уравнение с разделенными переменными. Представим его в дифференциалах. Для этого перепишем данное уравнение в виде Отсюда

Интегрируя обе части последнего равенства, найдем

Подставив начальные значения x₀ = 1, y₀ = 3 найдем С 9=1-1+C, т.е. С = 9.

Следовательно, искомый частный интеграл будет или

Составить уравнение кривой, проходящей через точку M(2;-3) и имеющей касательную с угловым коэффициентом

Решение. Согласно условию

Это уравнение с разделяющимися переменными. Разделив переменные, получим:

Проинтегрировав обе части уравнения, получим:

Используя начальные условия, x = 2 и y = — 3 найдем C:

Следовательно, искомое уравнение имеет вид

2.3. Линейные дифференциальные уравнения первого порядка

Линейным дифференциальным уравнением первого порядка называется уравнение вида y’ = f(x)y + g(x)

где f(x) и g(x) — некоторые заданные функции.

Если g(x)=0 то линейное дифференциальное уравнение называется однородным и имеет вид: y’ = f(x)y

Если то уравнение y’ = f(x)y + g(x) называется неоднородным.

Общее решение линейного однородного дифференциального уравнения y’ = f(x)y задается формулой: где С – произвольная постоянная.

В частности, если С =0, то решением является y = 0 Если линейное однородное уравнение имеет вид y’ = ky где k — некоторая постоянная, то его общее решение имеет вид: .

Общее решение линейного неоднородного дифференциального уравнения y’ = f(x)y + g(x) задается формулой ,

т.е. равно сумме общего решения соответствующего линейного однородного уравнения и частного решения данного уравнения.

Для линейного неоднородного уравнения вида y’ = kx + b,

где k и b— некоторые числа и частным решением будет являться постоянная функция . Поэтому общее решение имеет вид .

Пример. Решить уравнение y’ + 2y +3 = 0

Решение. Представим уравнение в виде y’ = -2y — 3 где k = -2, b= -3 Общее решение задается формулой .

Следовательно, где С – произвольная постоянная.

Ответ:

2.4. Решение линейных дифференциальных уравнений первого порядка методом Бернулли

Нахождение общего решения линейного дифференциального уравнения первого порядка y’ = f(x)y + g(x) сводится к решению двух дифференциальных уравнений с разделенными переменными с помощью подстановки y=uv, где u и v — неизвестные функции от x. Этот метод решения называется методом Бернулли.

Алгоритм решения линейного дифференциального уравнения первого порядка

1. Ввести подстановку y=uv.

2. Продифференцировать это равенство y’ = u’v + uv’

3. Подставить y и y’ в данное уравнение: u’v + uv’ = f(x)uv + g(x) или u’v + uv’ + f(x)uv = g(x).

4. Сгруппировать члены уравнения так, чтобы u вынести за скобки:

5. Из скобки, приравняв ее к нулю, найти функцию

Это уравнение с разделяющимися переменными:

Разделим переменные и получим:

Откуда . .

6. Подставить полученное значение v в уравнение (из п.4):

и найти функцию Это уравнение с разделяющимися переменными:

7. Записать общее решение в виде: , т.е. .

Найти частное решение уравнения y’ = -2y +3 = 0 если y =1 при x = 0

Решение. Решим его с помощью подстановки y=uv, .y’ = u’v + uv’

Подставляя y и y’ в данное уравнение, получим

Сгруппировав второе и третье слагаемое левой части уравнения, вынесем общий множитель u за скобки

Выражение в скобках приравниваем к нулю и, решив полученное уравнение, найдем функцию v = v(x)

Получили уравнение с разделенными переменными. Проинтегрируем обе части этого уравнения: Найдем функцию v:

Подставим полученное значение v в уравнение Получим:

Это уравнение с разделенными переменными. Проинтегрируем обе части уравнения: Найдем функцию u = u(x,c) Найдем общее решение: Найдем частное решение уравнения, удовлетворяющее начальным условиям y = 1 при x = 0:

Ответ:

III. Дифференциальные уравнения высших порядков

3.1. Основные понятия и определения

Дифференциальным уравнением второго порядка называется уравнение, содержащее производные не выше второго порядка. В общем случае дифференциальное уравнение второго порядка записывается в виде: F(x,y,y’,y») = 0

Общим решением дифференциального уравнения второго порядка называется функция вида , в которую входят две произвольные постоянные C₁ и C₂.

Частным решением дифференциального уравнения второго порядка называется решение, полученное из общего при некоторых значениях произвольных постоянных C₁ и C₂.

3.2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида y» + py’ +qy = 0, где pи q— постоянные величины.

Алгоритм решения однородных дифференциальных уравнений второго порядка с постоянными коэффициентами

1. Записать дифференциальное уравнение в виде: y» + py’ +qy = 0.

2. Составить его характеристическое уравнение, обозначив y» через r 2 , y’ через r, yчерез 1: r 2 + pr +q = 0

3.Вычислить дискриминант D = p 2 -4q и найти корни характеристического уравнения; при этом если:

а) D > 0; следовательно, характеристическое уравнение имеет два различных действительных корня . Общее решение дифференциального уравнения выражается в виде , где C₁ и C₂ — произвольные постоянные.

б) D = 0; следовательно, характеристическое уравнение имеет равные действительные корни . Общее решение дифференциального уравнения выражается в виде