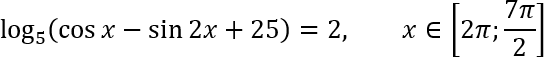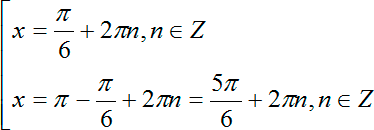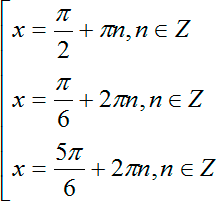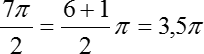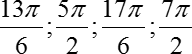Одз в тригонометрических уравнениях с логарифмами (7 видео)

«Некоторые методы решения логарифмических уравнений»

Разделы: Математика

Содержание

Некоторые методы решения логарифмических уравнений.
Решение логарифмических уравнений.
Задача C1: логарифмы и тригонометрия в одном уравнении
Решение логарифмического уравнения
Решение тригонометрического уравнения
Формула синуса двойного угла
Разложение уравнения на множители
Особенности решения тригонометрических уравнений с синусом
Область определения логарифмов — считать или не считать?
Отбор корней на отрезке
Особенности вычисления дробных корней
Заключительные выкладки
ОДЗ — Область допустимых значений
Область допустимых значений (ОДЗ) – это все значения переменной, при которых не нарушаются правила математики.
Как найти ОДЗ?
Если переменная (икс) в уравнении или неравенстве стоит в знаменателе, логарифме, под корнем, в тангенсе или котангенсе ОДЗ записать нужно.
🎥 Видео

Некоторые методы решения логарифмических уравнений.

Настоящая статья содержит систематическое изложение методов решения логарифмических уравнений с одной переменной. Это поможет учителю, прежде всего в дидактическом смысле: подбор упражнений позволяет составить для учащихся индивидуальные задания с учетом их возможностей. Данные упражнения могут быть использованы для урока обобщения и для подготовки к ЕГЭ.
Краткие теоретические сведения и решения задач позволяют учащимся самостоятельно развивать умения и навыки решения логарифмических уравнений.

Решение логарифмических уравнений.

Логарифмические уравнения – уравнения, содержащие неизвестное под знаком логарифма. При решении логарифмических уравнений часто используются теоретические сведения:

Обычно решение логарифмических уравнений начинается с определения ОДЗ. В логарифмических уравнениях рекомендуется все логарифмы преобразовать так, чтобы их основания были равны. Затем уравнения либо выражают через один какой – либо логарифм, который обозначается новой переменной, либо уравнение преобразовывают к виду, удобному для потенцирования.
Преобразования логарифмических выражений не должны приводить к сужению ОДЗ, если же примененный метод решения сужает ОДЗ, выпуская из рассмотрения отдельные числа, то эти числа в конце задачи необходимо проверить подстановкой в исходное уравнение, т.к. при сужении ОДЗ возможна потеря корней.

1. Уравнения вида – выражение, содержащее неизвестное число, а число .
Для решения таких уравнений надо:

1) воспользоваться определением логарифма: ;
2) сделать проверку или найти область допустимых значений для неизвестного числа и отобрать соответствующие им корни (решения).
Если ) .

2. Уравнения первой степени относительно логарифма, при решении которых используются свойства логарифмов.

Для решения таких уравнений надо:

1) используя свойства логарифмов, преобразовать уравнение;
2) решить полученное уравнение;
3) сделать проверку или найти область допустимых значений для неизвестного числа и отобрать соответствующие им корни (решения).
).

3. Уравнение второй и выше степени относительно логарифма.

Для решения таких уравнений надо:

сделать замену переменной;
решить полученное уравнение;
сделать обратную замену;
решить полученное уравнение;
сделать проверку или найти область допустимых значений для неизвестного числа и отобрать соответствующие им корни (решения).

4.Уравнения, содержащие неизвестное в основании и в показателе степени.

Для решения таких уравнений надо:

прологарифмировать уравнение;
решить полученное уравнение;
сделать проверку или найти область допустимых значений для неизвестного числа и отобрать соответствующие им
корни (решения).

5. Уравнения, которые не имеют решения.

Для решения таких уравнений надо найти ОДЗ уравнения.
Проанализировать левую и правую часть уравнения.
Сделать соответствующие выводы.

Исходное уравнение равносильно системе:

Доказать, что уравнение не имеет решения.

ОДЗ уравнения определяется неравенством х ≥ 0. На ОДЗ имеем

Сумма положительного числа и неотрицательного числа не равна нулю, поэтому исходное уравнение решений не имеет.

Ответ : решений нет.

В ОДЗ попадает только один корень х = 0. Ответ: 0.

Произведем обратную замену.

Найденные корни принадлежат ОДЗ.

ОДЗ уравнения – множество всех положительных чисел.

Аналогично решаются данные уравнения:

Задачи для самостоятельного решения:

Используемая литература.

Бесчетнов В.М. Математика. Москва Демиург 1994
Бородуля И.Т. Показательная и логарифмическая функции. ( задачи и упражнения). Москва «Просвещение» 1984
Вавилов В.В., Мельников И.И., Олехник С.Н., Пасиченко П.И. Задачи по математике. Уравнения и неравенства. Москва «Наука» 1987
Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер. Москва «Илекса»2007
Саакян С.М., Гольдман А.М., Денисов Д.В.. Задачи по алгебре и началам анализа. Москва «Просвещение» 2003

Видео:✓ Паника из-за ОДЗ | трушин ответит #018 | ЕГЭ. Задание 14. Математика. Профиль | Борис ТрушинСкачать

Задача C1: логарифмы и тригонометрия в одном уравнении

19 февраля 2014

Сегодня у нас будет насыщенный урок, потому что уравнение, которое мы будем сегодня разбирать, содержит в себе и логарифмическую, и тригонометрическую функцию. Но все по порядку.

Задача C1. Решите уравнение. Найдите все корни этого уравнения, принадлежащие промежутку.

На первый взгляд, задача кажется весьма нестандартной: тут и логарифмы, и тригонометрия. Но если разобраться, то окажется, что уравнения такого типа вполне под силу большинству учеников.

Видео:Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать

Решение логарифмического уравнения

Итак, нужно решить уравнение:

log₅ (cos x − sin 2 x + 25) = 2

Как видим, в первую очередь перед нами логарифмическое уравнение. Вспоминаем: как мы решаем логарифмическое уравнение? Очевидно, приводим его к каноническому виду, а именно:

log _a f ( x ) = log _a g ( x )

В нашем случае слева уже стоит логарифм по основанию 5. Следовательно, двойку тоже нужно представить в виде логарифма по тому же самому основанию 5. Вспоминаем, как это делается. С помощью нашей замечательной формулы:

Разумеется, мы можем подставить любое число b , удовлетворяющее требованиям, которые накладываются на основание логарифма:

Иначе наш логарифм просто не имеет смысла. Но какое именно b выбрать? Очевидно, что основание логарифма по нашей канонической записи должно быть равно основанию уже имеющегося логарифма, т. е. 5. Т.е. в нашем случае запишем:

Перепишем Все уравнение с учетом этого факта:

log₅ (cos x − sin 2 x + 25) = log₅ 25

Перед нами каноническое логарифмическое уравнение. В нем мы можем смело убрать знаки логарифма (т.е. просто приравнять аргументы логарифмов). Получим:

cos x − sin 2 x + 25 = 25

Видео:ЛОГАРИФМИЧЕСКОЕ УРАВНЕНИЕ: ОДЗ ИЛИ НЕ ОДЗ?Скачать

Решение тригонометрического уравнения

Перед нами тригонометрическое уравнение. Переносим 25 влево и получаем:

cos x − sin 2 x = 0

Теперь нам нужно решить обычное тригонометрическое уравнение. Все тригонометрические уравнения должны быть сведены к простейшему уравнению одного из трех видов:

Подобно тому, как в логарифмах есть каноническая запись, точно так же и в тригонометрии есть каноническая запись уравнений. Давайте еще раз посмотрим на наше уравнение:

cos x − sin 2 x = 0

Что-то канонической записью тут не пахнет. Во-первых, аргументы у наших тригонометрических функций разные. И это первая проблема. Следовательно, надо каким-то образом избавится от аргумента 2 x и свести его к х. Или, наоборот: сделать так, чтобы вместо переменной x стояло 2 x .

Еще раз: когда мы видим тригонометрическое уравнение, первое, что нам нужно — это постараться сделать так, чтобы во всех тригонометрических функциях были одинаковые аргументы: везде либо х, либо 2х. Любыми правдами и неправдами, любыми преобразованиями функций мы должны добиться того, чтобы аргументы были равными.

При решении тригонометрических уравнений сводите все функции к одному и тому же аргументу.

Формула синуса двойного угла

В данном случае все очень легко. Вспоминаем формулу синуса двойного угла:

sin 2 x = 2sin x · cos x

Подставляем это выражение в наше уравнение:

cos x − 2sin x · cos x = 0

Мы видим, что и в первом, и во втором слагаемом есть cos x . Выносим его за скобку:

cos x (1- 2sin x · 1) = 0

Кто-то скажет, что 1 в скобках писать излишне. Да, я не спорю, можно сразу записать так:

cos x (1- 2sin x ) = 0

Однако если вы только разбираетесь в тригонометрических уравнениях, то лучше использовать эту избыточность и записать ту самую единицу. Почему? Да потому что если вы не запишете 1 в конце перед скобкой, то велика вероятность, что вы забудете про единицу и в начале. В итоге у вас получится неверное выражение и, соответственно, мы получим неверный ответ.

А вот так, с дополнительной единичкой, никаких проблем не возникнет. В общем, запомните правило: если из какого-то выражения выносим переменную или функцию, вместо этой нее мы везде пишем единицу. И лишь затем, после того, как мы запишем эту конструкцию в скобках, мы можем убрать лишние единицы, если это возможно.

Рекомендую оставлять единицы на месте <> общих множителей, которые выносятся за скобку. Так вы застрахуете себя от обидных ошибок.

Разложение уравнения на множители

В нашем случае все возможно. Получим:

cos x (1- 2sin x ) = 0

Произведение равно нулю, когда хотя бы один из множителей равен нулю: либо cos x = 0, либо 1 − 2sin x = 0

Перед нами совокупность из двух простейших тригонометрических уравнений:

cos x = 0; 1 = 2sin x = 0.

Однако cos x = 0 — это уже каноническая запись вида cos x = a — именно так, как нужно для решения задачи. А вот второе уравнение — 1− 2sin x — нужно преобразовать. Предлагаю выразить отсюда sin x :

-2sin x = -1;
sin x = 1/2.

Мы получили окончательную совокупность:

cos x = 0; sin x = 1/2.

Таким образом, перед нами два канонических уравнения, которые легко решаются. Вспоминаем, что cos x = 0 — это частный случай, поэтому x = π/2 + π n , n ∈ Z .

Особенности решения тригонометрических уравнений с синусом

С другой стороны, sin x = 1/2 — это не частный, а общий случай. Кроме того, всем своим ученикам я рекомендую расписывать решения уравнений вида sin x = a через совокупность двух множеств:

sin x = a ⇒
x = arcsin a + 2π n , n ∈ Z;
x = π − arcsin a + 2π n , n ∈ Z .

Обратите внимание: в обоих вариантах периодом будет именно величина 2π, т.е. полный оборот на тригонометрическом круге! В нашем случае получим:

Итого мы получили совокупность из трех наборов корней:

Область определения логарифмов — считать или не считать?

Внимательные ученики наверняка заметят: изначально мы решали логарифмическое уравнение и, следовательно, должны учесть область определения логарифма. Потому что если где-то в уравнении встречается выражение вида log _a f ( x ) = log _a g ( x ), мы обязаны проверить, что f ( x ) > 0.

Почему же при решении данного уравнения мы нигде это не записали? Это же ошибка! Спокойно: в данном случае никакой ошибки нет. Требование к логарифму, чтобы аргумент был больше нуля, выполняется автоматически на следующем шаге:

cos x − sin 2 x + 25 = 25

Получается, что выражение под знаком логарифма в нашем случае должно быть равно 25. А 25 заведомо больше нуля, т. е. область определения автоматически выполняется для всех корней, которые мы получим в процессе решения уравнения.

И вообще, запомните: когда в уравнении присутствует лишь один логарифм, в аргументе которого имеется функция переменного х, можно вообще не заморачиваться с проверкой области определения, потому что эта область определения будет автоматически выполняться в процессе решения уравнения. Но это работает только для уравнений и только в том случае, если логарифм с функцией присутствует лишь в одном экземпляре на все уравнение.

Требования к области определения выполняются автоматически, если функция стоит в аргументе логарифма, а сам логарифм встречается в уравнении лишь один раз.

В нашем случае это требование выполняется, потому что мы решаем именно уравнение, а не неравенство, и логарифм с функцией в аргументе встречается только один. Собственно, исходное уравнение вообще содержит только один логарифм, поэтому считать область определения в данном случае излишне. Следовательно, мы решили уравнение — получили ответ к первой части задачи.

Видео:11 класс, 17 урок, Логарифмические уравненияСкачать

Отбор корней на отрезке

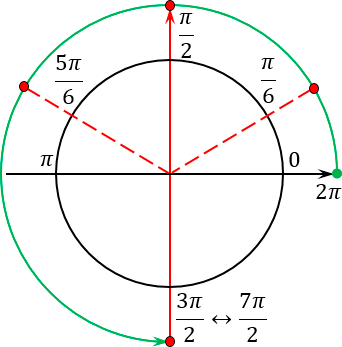
Переходим ко второй части задачи и находим корни, лежащие на заданном отрезке [2π; 7π/2]. Искать корни будем с помощью тригонометрического круга.

Первым делом обозначаем все три корня на тригонометрическом круге. Кроме того, отметим концы отрезка: 2π и 7π/2. Точка 2π совпадает с точкой началом отсчета, а в числе 7π/2 давайте выделим целую часть — по аналогии с обычными дробями:

Отметим полученное число на тригонометрическом круге. Теперь проведем лучи из начала координат в каждую точку. После этого ставим маркер в точку 2π и начинаем двигаться к точке 7π/2 против часовой стрелки. Получим:

Самый первый корень: 2π + π/6;
Затем — второй корень: 2π + π/2;
Следующий корень: 2π + 5π/6;
Наконец, последний корень совпадает с концом отрезка: 7π/2.

Особенности вычисления дробных корней

Ключевой момент в решении задачи таким методом состоит в том, каким образом мы отбираем корни. В первую очередь мы ставим маркер (ручку, карандаш или что там к вас) в самый левый конец отрезка — в нашем случае это 2π. Затем мы начинаем двигаться против часовой стрелки, т. е. в положительном направлении отсчета на тригонометрическом круге.

Первая точка, которую мы встречаем на своем пути, будет x = π/6. Чтобы записать корень, мы добавляем π/6 к началу отсчета 2π — это мы и записали. Идем дальше и прибавляем π/2. Потом, если идти еще дальше, мы попадаем точку 5π/6. И когда мы дойдем до конца, то обнаружим еще один корень — точку 7π/2.

Осталось посчитать те три корня из четырех, которые мы записали в виде выражения, потому что оставлять их в таком нерассчитанном виде нехорошо. Давайте посчитаем:

С последним корнем 7π/2 никаких дополнительных преобразований проводить не нужно — он уже рассчитан. Итого при отборе корней из всего бесконечного множества, разделенного на три набора, которые мы получили при решении нашего уравнения, остались лишь четыре конкретных корня:

Заключительные выкладки

Вот и все — задача решена. Как ни странно, решение получилось довольно простым, хотя изначально уравнение выглядело весьма угрожающе: в нем есть и логарифм, и тригонометрические функции. А получилось, что любой среднестатистический ученик вполне в состоянии справится с такими уравнениями.

И это правда. Достаточно помнить два простых факта:

Логарифмические уравнения мы всегда стараемся привести к каноническому виду: log_a f(x) = log_a g(x) — основания должны быть одинаковыми.
Тригонометрические уравнения тоже сводятся к каноническому виду. Точнее, к одной из трех моделей: sin x = a; cos x = a; tg x = a.

Однако нашем случае на пути к каноническому виду есть одна заминка. Дело в том, что в одной из функций, а именно sin 2 x , присутствует аргумент 2 x , в то время как в cos x есть только переменная х. Следовательно, придется вспомнить формулу двойного угла: sin 2 x = 2sin x · cos x — и уже на основании этой формулы наше исходное уравнение легко раскладывается на множители, откуда возникают канонические уравнения.

В общем, все, что требуется для решения уравнений подобного вида — это научиться работать с логарифмами, выучить несколько тригонометрических формул (особенно это касается формул синуса и косинуса двойного угла) и, конечно, не бояться преобразовать наше уравнение для того, чтобы получить красивые и легко решаемые конструкции.

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

ОДЗ — Область допустимых значений

Область допустимых значений (ОДЗ) – это все значения переменной, при которых не нарушаются правила математики.

— если в выражении (frac) значение переменной будет равно 1, нарушается правило: на ноль делить нельзя. Поэтому здесь (x) не может быть единицей и ОДЗ записывается так: (xneq1);

— если в выражении (sqrt) значение переменной равно (0), нарушается правило: подкоренное выражение не должно быть отрицательно. Значит, здесь (x) не может быть (0), а также (1, -3, -52,7) и т.д. То есть, икс должен быть больше или равен 2 и ОДЗ будет: (xgeq2);

— а вот в выражение (4x+1) мы можем подставить любое число вместо икса, и никакие правила нарушены не будут. Поэтому область допустимых значений здесь — вся числовая ось. В таких случаях ОДЗ не записывают, потому что оно не несет в себе полезной информации.

Видео:🙂 Тригонометрическое уравнение ОДЗСкачать

Как найти ОДЗ?

Если переменная (икс) в уравнении или неравенстве стоит в знаменателе, логарифме, под корнем, в тангенсе или котангенсе ОДЗ записать нужно.

Чтобы осознать важность ОДЗ, давайте сравним два решения уравнения: с ОДЗ и без ОДЗ.

Без ОДЗ:	С ОДЗ:
(frac=frac)	(frac=frac)
ОДЗ: (x+3≠0) (⇔) (x≠-3)
(x^2-x=12)	(x^2-x=12)
(x^2-x-12=0)	(x^2-x-12=0)
(D=(-1)^2-4·1·(-12)=49)	(D=(-1)^2-4·1·(-12)=49)
(x_1=) (frac<-(-1) + sqrt>) (=4)	(x_2=) (frac<-(-1) + sqrt>) (=4)
(x_1=) (frac<-(-1) — sqrt>) (=-3)	(x_2=) (frac<-(-1) — sqrt>) (=-3) — не подходит под ОДЗ
Ответ: (4; -3)	Ответ: (4)

Видите разницу? В первом решении у нас в ответе появился неверный, лишний корень ! Почему неверный? А давайте попробуем подставить его в исходное уравнение.

Видите, у нас получились и слева, и справа невычислимые, бессмысленные выражения (ведь на ноль делить нельзя). И то, что они одинаковы уже не играет роли, поскольку эти значения — не существуют. Таким образом, «(-3)» – неподходящий, посторонний корень, а область допустимых значений оберегает нас от таких серьезных ошибок.

Именно поэтому за первое решение вы получите двойку, а за второе – пятерку. И это не занудные придирки учителя, ведь неучет одз – не мелочь, а вполне конкретная ошибка, такая же как потерянный знак или применение не той формулы. В конце концов, итоговый ответ-то неверен!

Нахождение области допустимых значений часто приводит к необходимости решать системы неравенств или уравнений, поэтому вы должны уметь это делать хорошо.

Решение: В выражении два корня, один из которых в знаменателе. Кто не помнит ограничения, накладывающиеся в этом случае, тот смотрит таблицу . Кто помнит, записывает, что выражение под первым корнем больше или равно нулю, а под вторым — больше нуля. Понимаете, почему ограничения именно такие?

Дело за малым, нужно решить систему неравенств.
В первом неравенстве перенесем (5) вправо, второе умножим на (-1)

Запишем общий ответ для системы – это и есть допустимые значения для икса.