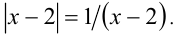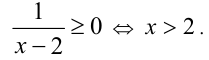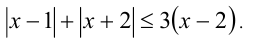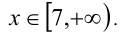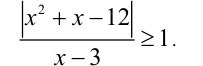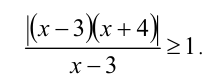Одз для модуля в уравнении

Видео:МодульСкачать

Раскрытие модулей на ОДЗ

Раскрытие модулей на ОДЗ

При решении задач с модулями не всегда сразу возникает необходимость в применении метода интервалов или каких-либо других способов избавления от модулей. Иногда бывает достаточно провести анализ ОДЗ, и в результате по крайней мере часть модулей удаётся однозначно раскрыть. Рассмотрим три примера.

Пример №274.

Решить уравнение

Решение:

Очевидно, Более того, так как левая часть уравнения неотрицательна, то и равная ей правая часть должна быть неотрицательна, т.е.

Но при модуль раскрывается положительно, и, решая полученное уравнение находим или Только второе число удовлетворяет условию и поэтому будет решением.

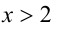
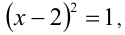
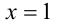
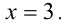
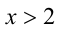
Пример №275.

Решить уравнение

Решение:

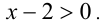
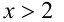
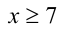
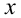
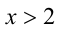
Заметим, что левая часть уравнения положительна (как сумма двух неотрицательных слагаемых, одновременно не обращающихся в нуль). Следовательно, Но при оба модуля раскрываются положительно, и, решая полученное неравенство, находим . Так как все такие удовлетворяют условию , то они являются решениями. Ответ:

Пример №276.

Решение:

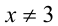
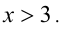
Очевидно,. Более того, так как дробь, по условию, больше 1, то она, как минимум, положительна. При этом числитель дроби положителен, а значит, и знаменатель должен быть положительным, т.е. Перепишем неравенство в виде:

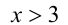
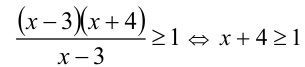
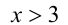
Видно, что при подмодульное выражение положительно, следовательно, модуль однозначно раскрывается, и получаем неравенство — верно при. Ответ:

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Эти страницы возможно вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Способы решения уравнений содержащих модуль

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Способы решения уравнений содержащих модуль.

1. Основные способы, используемые при решении уравнений, содержащих модуль.

Напомним основные понятия, используемые в данной теме.

Уравнением с одной переменной называют равенство, содержащее переменную.

Корнями уравнения называются значения переменной, при которых уравнение обращается в верное равенство.

Решить уравнение – значит, найти все его корни или доказать, что корней нет.

Уравнением с модулем называют равенство, содержащее переменную под знаком модуля.

При решении уравнений, содержащих знак абсолютной величины, мы будем основываться на определении модуля числа и свойствах абсолютной величины числа.

Свойства модуля

Существует несколько способов решения уравнений с модулем. Рассмотрим каждый из них.

1 СПОСОБ. МЕТОД ПОСЛЕДОВАТЕЛЬНОГО РАСКРЫТИЯ МОДУЛЯ.

Пример 1. Решим уравнение |х-5|=4.
Исходя из определения модуля, произведем следующие рассуждения. Если выражение, стоящее под знаком модуля неотрицательно, то есть х-5≥0, то уравнение примет вид х-5=4. Если значение выражения под знаком модуля отрицательно, то по определению оно будет равно – (х-5)=4 или х-5= -4. Решая полученные уравнения, находим: х1=9, х2=1.
Ответ: 9; 1.
Решим этим же способом уравнение, содержащее «модуль в модуле».

Пример 2. Решим уравнение ||2х-1|-4|=6.
Рассуждая аналогично, рассмотрим два случая.
1). |2х-1|-4=6, |2х-1|=10. Используя еще раз определение модуля, получим: 2х-1=10 либо 2х-1= -10. Откуда х1=5,5, х2= -4,5.
2). |2х-1|-4= -6, |2х-1|= -2. Понятно, что в этом случае уравнение не имеет решений, так как по определению модуль всегда неотрицателен.
Ответ: 5,5; -4,5.

2 СПОСОБ. МЕТОД ИНТЕРВАЛОВ.

Метод интервалов – это метод разбиения числовой прямой на промежутки, в которых по определению модуля знак абсолютной величины можно будет снять. Для каждого из промежутков необходимо решить уравнение и сделать вывод относительно получившихся корней. Корни, удовлетворяющие промежуткам, и дадут окончательный ответ.

Пример 3. Решим уравнение |х+3|+|х-1|=6.
Найдем корни (нули) каждого выражения, содержащегося под знаком модуля: х+3=0, х= -3; х-1=0, х=1. Эти значения х разбивают числовую прямую на три промежутка:
-3 1
Решим уравнение отдельно в каждом из получившихся промежутков. В первом промежутке (х

Пример 4. |2-х|=2х+1.
Прежде всего, следует установить область допустимых значений. Возникает естественный вопрос, почему в предыдущих примерах не было необходимости этого делать. В этом уравнении в правой части стоит выражение с переменной, которое может быть отрицательным. Таким образом, область допустимых значений – это промежуток [-½; +∞). Найдем нуль выражения, стоящего под знаком модуля: 2-х=0, х=2.
В первом промежутке: 2-х=2х+1, х=⅓. Это значение принадлежит ОДЗ, значит, является корнем уравнения.
Во втором промежутке: -2+х=2х+1, х= -3. -3 не принадлежит ОДЗ, а следовательно не является корнем уравнения. Ответ: ⅓.

3 СПОСОБ. ГРАФИЧЕСКИЙ МЕТОД.

Суть данного метода заключается в использовании графиков функций для нахождения корней уравнения. Этот метод реже других применяют для решения уравнений, содержащих модуль, так как, во-первых, он занимает достаточно много времени и не всегда рационален, а, во-вторых, результаты, полученные при построении графиков, не всегда являются точными.

Преобразуем уравнение: 1 + |x| = 0.5

Графиком функции являются лучи — биссектрисы 1-го и 2-го координатных углов. Графиком функции является прямая, параллельная оси OX и проходящая через точку -0,5 на оси OY.

Графики не пересекаются, значит, уравнение не имеет решений.

Ответ: нет решений.

Пример 5. |х+1|=2. Построим графики функций у=|х+1| и у=2.
Для построения графика у=|х+1|, построим график функции у=х+1, а затем отразим часть прямой, лежащую ниже оси ОХ. Абсциссы точек пересечения графиков и есть корни уравнения: х ₁ =1, х ₂ = -3. Ответ: 1; -3.

Пример 6. |х 2 -1|=|4-х 2 |.
Построим графики функций у=|х 2 -1| и у=|4-х 2 |. Для этого построим графики функций у= х 2 -1 и у=4-х 2 , а затем отобразим часть графиков, лежащую ниже оси ОХ.
х ₁ ≈1,6; х ₂ ≈-1,6.

4 СПОСОБ. МЕТОД РЕШЕНИЯ ПРИ ПОМОЩИ ЗАВИСИМОСТЕЙ МЕЖДУ ЧИСЛАМИ А И В, ИХ МОДУЛЯМИ И КВАДРАТАМИ ЭТИХ ЧИСЕЛ.

| а |=| в | а=в или а=-в;

а 2 =в 2 а=в или а=-в; (1)

| а |=| в | а 2 =в 2 (2)

Пример 7 . Решим уравнение |х 2 -8х+5|=|х 2 -5|.

Учитывая соотношение (1), получим:

х 2 -8х+5= х 2 -5 или х 2 -8х+5= -х 2 +5

Таким образом, корни исходного уравнения: х ₁ =1,25; х ₂ =0; х ₃ =4.

В силу соотношения (2) получаем: (х+3) 2 =(х-5) 2 ;

х 2 +6х+9= х 2 -10х+25;

Пример 9 . (1-3х) 2 =(х-2) 2 .

Учитывая соотношение (2), получаем: |1-3х|=|х-2|, откуда из соотношения (1), имеем:

1-3х=х-2 или 1-3х= -х+2

5 СПОСОБ. ИСПОЛЬЗОВАНИЕ ГЕОМЕТРИЧЕСКОЙ ИНТЕРПРЕТАЦИИ МОДУЛЯ.

Опорная информация: геометрический смысл модуля разности величин – это расстояние между ними. Например, геометрический смысл выражения |х-а| — длина отрезка координатной оси, соединяющей точки с абсциссами а и х. Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких решений.

Исходя из геометрической интерпретации модуля, левая часть уравнения представляет собой сумму расстояний от некоторой точки с абсциссой х до двух фиксированных точек с абсциссами 2 и 3. Тогда очевидно, что все точки с абсциссами, принадлежащими отрезку [2;3] обладают требуемым свойством, а точки, расположенные вне этого отрезка – нет. Отсюда, множеством решений уравнения является отрезок [2;3].

Рассуждая аналогично, получим, что разность расстояний до точек с абсциссами 2 и 3 равна 1 только для точек, расположенных на координатной оси правее числа 3. Следовательно, решением данного уравнения будет являться луч, выходящий из точки 3, и направленный в положительном направлении оси ОХ.

Обобщением вышеприведенных уравнений 10 и 11 являются следующие равносильные переходы:

|х-а|+|х-в|=в-а, где в ≥ а а ≤ х ≤ в

|х-а|-|х-в|=в-а, где в ≥ а х ≥ в

Проанализировав представленные способы решения уравнений, содержащих модуль, можно сделать вывод, что ни один из них не является универсальным и для получения наилучших результатов необходимо добиваться того, чтобы ученик овладел возможно большим количеством методов решения, оставляя право выбора решения за собой.

Решим аналитически и графически уравнение |x — 2| = 3.

А) Аналитическое решение

Рассуждать будем, исходя из определения модуля. Если выражение, находящееся под модулем

неотрицательно, т. е. x — 2 0, тогда оно «выйдет» из под знака модуля со знаком «плюс» и уравнение примет вид: x — 2 = 3. Если значения выражения под знаком модуля отрицательно, тогда, по определению, оно будет равно: или x — 2=-3

Таким образом, получаем, либо x — 2 = 3, либо x — 2 = -3. Решая полученные уравнения, находим:

Ответ:

Теперь можно сделать вывод: если модуль некоторого выражения равен действительному положительному числу a, тогда выражение под модулем равно либо a, либо .

Одним из способов решения уравнений, содержащих модуль, является графический способ. Суть этого способа заключается в том, чтобы построить графики данных функций. В случае, если графики пересекутся, точки пересечений данных графиков будут являться корнями нашего уравнения. В случае, если графики не пересекутся, мы сможем сделать вывод, что уравнение корней не имеет. Этот способ, вероятно, реже других применяют для решения уравнений, содержащих модуль, так как, во-первых, он занимает достаточно много времени и не всегда рационален, а, во-вторых, результаты, полученные при построении графиков, не всегда являются точными.

Другой способ решения уравнений, содержащих модуль — это способ разбиения числовой прямой на промежутки. В этом случае нам нужно разбить числовую прямую так, что по определению модуля, знак абсолютной величины на данных промежутках можно будет снять. Затем, для каждого из промежутков мы должны будем решить данное уравнение и сделать вывод, относительно получившихся корней (удовлетворяют они нашему промежутку или нет). Корни, удовлетворяющие промежутки и дадут окончательный ответ.

Установим, при каких значениях x, модуль равен нулю:

Получим два промежутка, на каждом из которых решим уравнение:

Получим две смешанных системы:

(1) (2)

Решим каждую систему:

(1) (удовлетворяет данному промежутку)

(2)

Ответ:

Для решения уравнения графическим способом, надо построить графики функций и

Для построения графика функции , построим график функции — это прямая, пересекающая ось OX в точке (2; 0), а ось OY в точке а затем часть прямой, лежащую ниже оси OX зеркально отразить в оси OX.

Графиком функции является прямая, параллельная оси OX и проходящая через точку (0; 3) на оси OY.

Абсциссы точек пересечения графиков функций дадут решения уравнения.

Прямая графика функции y=3 пересеклась с графиком функции y=|x – 2| в точках с координатами (-1; 3) и (5; 3), следовательно, решениями уравнения будут абсциссы точек:

Ответ:

Практика обучения учащихся способам решения уравнений, содержащих модули, позволила выявить достоинства и недостатки каждого способа, которые для удобства сведены в таблицу.

Метод последовательного раскрытия модулей

1). Объявляя условие раскрытия одного модуля, можно пользоваться им для раскрытия других модуле тем самым, выигрывая время в решении задачи.

2). Последовательность действий, направленных на поиск ответа, позволяет контролировать и проверять промежуточные результаты.

Необходимость раскрытия модуля, что для некоторых заданий приводит к потере темпа в получении ответа.

Самый эффективный способ, так как сопровождается относительно небольшим объемом работы.

В силу необходимости нахождения концов интервалов может возникнуть ситуация, когда соответствующее уравнение либо вызывает серьезные затруднения при определении корней, либо недоступно ученику на данном этапе обучения.

Данный способ имеет очень широкое применение в других темах школьного курса математики.

Ответ определяется приблизительно.

Метод решения при помощи зависимостей между числами, их модулями и квадратами этих чисел

В некоторых случаях применение данного способа позволяет решать уравнения определенного вида на более раннем этапе.

В некоторых случаях выбор данного способа приводит к громоздкому решению, а иногда решение сводится к уравнению, недоступному для ученика на данном этапе обучения.

Геометрическая интерпретация модуля

Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких решений.

Применение данного способа ограничивается уравнениями определенного вида.

Проанализировав достоинства и недостатки каждого из указанных способов, можно с уверенностью сказать, что на мотивационном этапе формирования умения решать уравнения с модулем ученикам следует показывать все, доступные на данном этапе обучения способы решения, и, главное, на конкретных примерах доказывать, что первый этап решения – выбор самого эффективного способа.

Рассмотрим пример |(х-1)(х-3)|=х-3.

Это уравнение можно решить тремя способами.
а) последовательное раскрытие модуля:
Если (х-1)(х-3) ≥ 0, то Если (х-1)(х-3) 2 -4х+3=х-3, х 2 -4х+3= -х+3,
х 2 -5х+6=0, х 2 -3х=0,
х ₁ =3, х ₂ =2. х ₁ =0, х ₂ =3.
2 – не удовлетворяет условию. 0, 3 — не удовлетворяет условию.
Ответ: 3.
б) метод интервалов: найдем концы интервалов, решив уравнение (х-1)(х-3)=0, откуда х ₁ =1, х ₂ =3.

(х-1)(х-3)=х-3, -(х-1)(х-3)=х-3, (х-1)(х-3)=х-3,
х ₁ =2, х ₂ =3. х ₁ =0, х ₂ =3. х ₁ =2, х ₂ =3.
2 (-∞; 1), 0 [1; 3). 2 [3; +∞).
3 (-∞; 1).
Ответ: 3.
в) графический метод: для решения уравнения построим в одной системе координат графики функций у=|х 2 -4х+3| и у=-3.
Построим у=|х 2 -4х+3|. Для этого сначала рассмотрим функцию у=х 2 -4х+3, графиком которой является парабола, ветви направлены вверх. Вершина параболы в точке (2; -1). Строим график и отображаем часть параболы, которая лежит ниже оси ОХ в верхнюю полуплоскость. Далее в этой же системе координат строим график у=х-3. Графики функций пересеклись в точке с абсциссой 3.
Ответ: 3.

Таким образом, можно сделать следующий вывод: систематическое использование различных способов для решения уравнений, содержащих абсолютную величину, приводит не только к повышению интереса к математике, повышению творческой активности школьников, но и повышает уверенность детей в собственных силах, так как у них имеется возможность выбора того способа решения, который наиболее эффективен в каждом конкретном случае.

ТЕСТОВЫЕ ЗАДАНИЯ по теме «Решение уравнений с модулем».
1. Какие числа являются решениями уравнения |х+3|= -4?
а) -7; б) -7; 1; в) нет корней; г) 1.
2. Решите уравнение |х+3|=7:
а) 7; б) -7; в) 0; 7; г) 7; -7.
3. Определите координаты точки пересечения графиков функций у=|2х+1| и у=0:
а) (0;0); б) (-0,5;0); в) (0;-0,5); г) (0,5;0).
4. Решите уравнение |х+3|+|х-1|=6:
а) 3; -2; б) 4; -2; в) -4; 2; г) 2; -3.
5. Сколько точек пересечения имеют графики функций у=||5,5х-4|+2| и у=3?
а) 1; б) 2; в) 3; г) 4.
6. Решите уравнение |3х-7|=1-х:
а) 2; 3; б) -2; 3; в) -3; 2; г) -2; -3.
7. Сколько решений имеет уравнение (2,5х-5)2=(0,5х-6)2:
а) 1; б) 2; в) 3; г) 4.

СИСТЕМА КАРТОЧЕК-ЗАДАНИЙ по теме «Решение уравнений с модулем».
1. ЗАДАНИЯ С УКАЗАНИЯМИ ИЛИ АЛГОРИТМИЧЕСКИМИ ПРЕДПИСАНИЯМИ И ОБРАЗОМ ВЫПОЛНЕНИЯ.
УКАЗАНИЯ ОБРАЗЕЦ ЗАДАНИЕ
Если |х-а|+|х-в|=в-а, где в ≥ а, то
а ≤ х ≤ в
|х-1|+|х-2|=1,
1 ≤ х ≤ 2.
Ответ: [1; 2]
а) |х-4|+|х-5|=1,
б) |х|-|х-1|=1,
в) |х-6|+|х-8|=2,
г) |х-0,5|-|х-4,5|=4.

Если |х-а|-|х-в|=в-а, где в ≥ а, то
х ≥ в
|х-1|-|х-2|=1,
х ≥ 2.
Ответ: [2; +∞).

АЛГОРИТМ ОБРАЗЕЦ ЗАДАНИЯ
1. Отметить все нули подмодульных выражений на числовой прямой. Они разобьют числовую прямую на промежутки, в которых все подмодульные выражения имеют постоянный знак.
2. Из каждого промежутка взять произвольное число и подсчетом определить знак подмодульного выражения, по знаку раскрыть модули.
3. Решить уравнения и выбрать решения, принадлежащие данному промежутку. |х+1|+|х+2|=1.
Решение.
Подмодульные выражения х+1 и х+2 обращаются в нуль при х= -1, х= -2.

1) -3 (-∞; -2]
-х-1-х-2=1; х= -2;
-2 (-∞; -2].
2) -1,5 (-2; -1)
-х-1+х+2=1; 1=1; х — любое число из промежутка (-2; -1).
3) 0 [-1; +∞)
х+1+х+2=1; х= -1;
-1 [-1; +∞).
Ответ: [-2; -1].
1) |14-х|+|х+1|=7;
2) |х|-|х+2|=2;
3) |х2-4|=|2х-1|;
4) | х2-6х+5|+|3-х|=3

2. ЗАДАНИЯ «НАЙДИ ОШИБКУ».
1.
Решить уравнение: |х2-8х+5|=| х2-5|.
Решение.
|х2-8х+5|=| х2-5|
х2-8х+5= х2-5, или х2-8х+5=5- х2,
-8х+10=0, 2 х2-8х=0,
х=1,25. х(2х-8)=0,
х=0, или 2х-8=0,
2х=8,
х=0,25.
Ответ: 1,25; 0,25. ВЕРНОЕ РЕШЕНИЕ

2.
Решить уравнение х2-6х+|х-4|+8=0.
Решение.
Если х-4 ≥ 0, то Если х-4 Решить уравнение |х-1|-2|х+3|+х+7=0.
Решение.
Решим уравнение методом интервалов, для этого найдем концы интервалов, решив уравнения
х-1=0 и х+3=0
х=1 х= -3.
-х+1-2(-х-3)+х+7=0; -х+1-2х-6+х+7=0; х-1-2х-6+х+7=0;
2х+14=0; -2х+2=0; 0=0.
х= -7. х=1. х — любое число.
Ответ: х – любое число. ВЕРНОЕ РЕШЕНИЕ

3. ЗАДАНИЯ С СОПУТСТВУЮЩИМИ УКАЗАНИЯМИ И ИНСТРУКЦИЯМИ.
1.
Решить уравнение |х-2|+|2х-7|=3.
Решение.
Решим уравнение методом интервалов.
1) Найдите нули подмодульных выражений, решив уравнения:
х-2=0 и 2х-7=0.
х1=… х2=…
2) Отметьте полученные значения на координатном луче.

3) Решите исходное уравнение на каждом из интервалов, предварительно определив знак подмодульного выражения. Учитывая знак, раскрыть модули.

4) Проверьте, принадлежат ли найденные корни указанным промежуткам.
Ответ: …………………………………………………….

2.
Решить уравнение ||х-3|-х+1|=6.
Решение.
1) Раскройте внешний модуль, используя определение: |а|=а, если а ≥ 0 и
|а|= -а, если а 4. ЗАДАНИЯ С ПРИМЕНЕНИЕМ КЛАССИФИКАЦИИ.
1.
Выпишите уравнения, которые решаются с помощью зависимостей между величинами, их модулями и квадратами величин. Решите эти уравнения.
1) ||х|+3|=3;
2) |х|+|х+4|=х-1;
3) |х+2|=|3-х|;
4) |х+3|+|х-1|=7;
5) (2х-3)2=(3,5х-1)2;
6) |х2-4х+5|=|х2-9|;
7) |11х-7|= -3;
8) |х-2|+|х-1|=1;
9) х2-х-2=|5х-3|;

2.
Выпишите уравнения, которые решаются с использованием геометрической интерпретации модуля. Решите эти уравнения.
1) |х|-|х-8|=2;
2) |х 2 -2х-3|=3х-3;
3) |2х-|2х-|2х-3|||=0;
4) |х-1|-2|х+4|+х+11=0;
5) |х-3|+|х-4|=1;
6) (5х-4) 2 =(2х-1) 2 ;
7) |2,5х-11|= -2;
8) |х-7|-|х-9|=2.

5. ЗАДАНИЯ С ВЫПОЛНЕНИЕМ НЕКОТОРОЙ ЧАСТИ.
1.
Решить уравнение (х 2 -5х+6)2-5•| х 2 -5х+6|+6=0.
Решение.
Пусть | х 2 -5х+6|=t, тогда, учитывая, что (х 2 -5х+6)2=| х 2 -5х+6|2, получим уравнение: t 2 -5t+6=0. Решением этого уравнения являются числа ……. поэтому исходное уравнение равносильно совокупности двух уравнений:
| х 2 -5х+6|=… или | х 2 -5х+6|=…
…………………………………………………………………………………
…………………………………………………………………………………
…………………………………………………………………………………
…………………………………………………………………………………

ПРОВЕРОЧНАЯ РАБОТА по теме «Решение уравнений с модулем»
1. Решите уравнение |х-3|=7.
2. Решите графически уравнение |2х+1|=3.
3. Решите уравнение методом интервалов |х+1|+|х-1|=3.
4. Решите уравнение методом последовательного раскрытия модулей |-х+2|=2х+1.
5. Решите уравнение (2х+3) 2 =(х-1) 2 .
6. Решите уравнение самым удобным способом |х 2 +6х+2|=3|х+2|.
7. При каком значении а уравнение можно решить, используя геометрическую интерпретацию модуля: |х-а|+|х-9|=1?

Видео:Уравнения с модулемСкачать

Уравнения с модулем

Эта статья посвящена приёмам решения различных уравнений и неравенств, содержащих
переменную под знаком модуля.

Если на экзамене вам попадётся уравнение или неравенство с модулем, его можно решить,
вообще не зная никаких специальных методов и пользуясь только определением модуля. Правда,
занять это может часа полтора драгоценного экзаменационного времени.

Поэтому мы и хотим рассказать вам о приёмах, упрощающих решение таких задач.

Прежде всего вспомним, что

Рассмотрим различные типы уравнений с модулем. (К неравенствам перейдём позже.)

Видео:ДРОБНО-РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ ЧАСТЬ I #shorts #егэ #огэ #математика #профильныйегэСкачать

Слева модуль, справа число

Это самый простой случай. Решим уравнение

Есть только два числа, модули которых равны четырём. Это 4 и −4. Следовательно, уравнение
равносильно совокупности двух простых:

Второе уравнение не имеет решений. Решения первого: x = 0 и x = 5.

Видео:Как решить неравенства с модулем?Скачать

Переменная как под модулем, так и вне модуля

Здесь приходится раскрывать модуль по определению. . . или соображать!

Уравнение распадается на два случая, в зависимости от знака выражения под модулем.
Другими словами, оно равносильно совокупности двух систем:

Решение первой системы: . У второй системы решений нет.
Ответ: 1.

Первый случай: x ≥ 3. Снимаем модуль:

Число , будучи отрицательным, не удовлетворяет условию x ≥ 3 и потому не является корнем исходного уравнения.

Выясним, удовлетворяет ли данному условию число . Для этого составим разность и определим её знак:

Значит, больше трёх и потому является корнем исходного уравнения

Стало быть, годятся лишь и .

Ответ:

Видео:Неравенства с модулем | Математика | TutorOnlineСкачать

Квадратные уравнения с заменой |x| = t

Поскольку , удобно сделать замену |x| = t. Получаем:

Видео:Модуль в модуле в уравнении. Алгебра 7 класс.Скачать

Модуль равен модулю

Речь идёт об уравнениях вида |A| = |B|. Это — подарок судьбы. Никаких раскрытий модуля по определению! Всё просто:

Например, рассмотрим уравнение: . Оно равносильно следующей совокупности:

Остаётся решить каждое из уравнений совокупности и записать ответ.

Видео:Как решать уравнение с модулем Уравнение с модулями как решать Как раскрыть модуль в уравненииСкачать

Два или несколько модулей

Не будем возиться с каждым модулем по отдельности и раскрывать его по определению — слишком много получится вариантов. Существует более рациональный способ — метод интервалов.

Выражения под модулями обращаются в нуль в точках x = 1, x = 2 и x = 3. Эти точки делят числовую прямую на четыре промежутка (интервала). Отметим на числовой прямой эти точки и расставим знаки для каждого из выражений под модулями на полученных интервалах. (Порядок следования знаков совпадает с порядком следования соответствующих модулей в уравнении.)

Таким образом, нам нужно рассмотреть четыре случая — когда x находится в каждом из интервалов.

Случай 1: x ≥ 3. Все модули снимаются «с плюсом»:

Полученное значение x = 5 удовлетворяет условию x ≥ 3 и потому является корнем исходного уравнения.

Случай 2: 2 ≤ x ≤ 3. Последний модуль теперь снимается «с минусом»:

Полученное значение x также годится — оно принадлежит рассматриваемому промежутку.

Случай 3: 1 ≤ x ≤ 2. Второй и третий модули снимаются «с минусом»:

Мы получили верное числовое равенство при любом x из рассматриваемого промежутка [1; 2] служат решениями данного уравнения.

Случай 4: x ≤ 1 ≤ 1. Второй и третий модули снимаются «с минусом»:

Ничего нового. Мы и так знаем, что x = 1 является решением.

Видео:Уравнения с модулем. Что такое модуль числа. Алгебра 7 класс.Скачать

Модуль в модуле

Начинаем с раскрытия внутреннего модуля.

1) x ≤ 3. Получаем:

Выражение под модулем обращается в нуль при . Данная точка принадлежит рассматриваемому
промежутку. Поэтому приходится разбирать два подслучая.

1.1) Получаем в этом случае:

Это значение x не годится, так как не принадлежит рассматриваемому промежутку.

1.2) . Тогда:

Это значение x также не годится.

Итак, при x ≤ 3 решений нет. Переходим ко второму случаю.

Здесь нам повезло: выражение x + 2 положительно в рассматриваемом промежутке! Поэтому никаких подслучаев уже не будет: модуль снимается «с плюсом»:

Это значение x находится в рассматриваемом промежутке и потому является корнем исходного уравнения.

Так решаются все задачи данного типа — раскрываем вложенные модули по очереди, начиная с внутреннего.

Читайте также о том, как решать неравенства с модулем.

🌟 Видео

УРАВНЕНИЯ С МОДУЛЕМ | метод интерваловСкачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Контрольная работа. Уравнения с МОДУЛЕМСкачать

СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Уравнения с модулем за 1 минуту. #математикапрофиль2023 #егэ2023 #математика #школа #fypСкачать

Сложное уравнения с модулем. Алгебра 7 класс.Скачать

Уравнение с двумя модулями: особенности решенияСкачать

✓ Паника из-за ОДЗ | трушин ответит #018 | ЕГЭ. Задание 14. Математика. Профиль | Борис ТрушинСкачать

Уравнения с модулем. Часть 2 | Математика | TutorOnlineСкачать

Алгебра 8. Урок 11 - Дробно-рациональные уравненияСкачать

Линейные уравнения с одной переменной, содержащие переменную под знаком модуля. 6 класс.Скачать