Логарифмическое неравенство может встретиться вам в 13 задании ЕГЭ по математике. При решении логарифмического неравенства важно правильно определить область допустимых значений (ОДЗ). Как же решить логарифмическое неравенство? Давайте разберем основные правила.
- Как найти ОДЗ (область допустимых значений) логарифмического неравенства
- Решение логарифмического неравенства с основанием от 0 до 1
- Логарифмические неравенства
- Логарифмические уравнения и неравенства
- Логарифмическая функция
- Определение
- Основные свойства
- Решение логарифмических уравнений и неравенств
- 📺 Видео
Видео:11 класс, 18 урок, Логарифмические неравенстваСкачать
Как найти ОДЗ (область допустимых значений) логарифмического неравенства
Простейшее логарифмическое неравенство можно записать в виде:
знак можно заменить на 1, то знак неравенства не меняется.
Если у логарифма в неравенстве 0 0
Решаем это простейшее неравенство и получаем х > -2.
Таким образом область допустимых значений данного неравенства х > -2.
Далее решаем непосредственно логарифмическое неравенство. Так как основание логарифмов (основание = 2) в неравенстве больше единицы, знак неравенства сохраняется:
Так как логарифмы в неравенстве имеют одинаковое основание, то мы их можем просто отбросить и решить неравенство вида
Теперь вспоминаем про нашу ОДЗ и определяем окончательный ответ.
Отметим полученные значения на числовой оси:
Видео:Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать
Решение логарифмического неравенства с основанием от 0 до 1
Теперь разберем то же самое неравенство, только основание логарифма будет равно ½. Таким образом, получим:
Определяем ОДЗ, как и в прошлом примере, х > -2.
Далее смотрим на основание логарифма. В данном случае основание равно ½, т.е. находится в области от 0 1 или 0 , -4½
Видео:ЛОГАРИФМИЧЕСКОЕ УРАВНЕНИЕ: ОДЗ ИЛИ НЕ ОДЗ?Скачать
Логарифмические неравенства
Решая логарифмические неравенства, мы пользуемся свойством монотонности логарифмической функции. Также мы используем определение логарифма и основные логарифмические формулы.
Давайте повторим, что такое логарифмы:
Логарифм положительного числа по основанию — это показатель степени, в которую надо возвести , чтобы получить .
Основное логарифмическое тождество:
Основные формулы для логарифмов:
(Логарифм произведения равен сумме логарифмов)
(Логарифм частного равен разности логарифмов)
(Формула для логарифма степени)
Формула перехода к новому основанию:
Алгоритм решения логарифмических неравенств
Можно сказать, что логарифмические неравенства решаются по определенному алгоритму. Нам нужно записать область допустимых значений (ОДЗ) неравенства. Привести неравенство к виду Знак здесь может быть любой: Важно, чтобы слева и справа в неравенстве находились логарифмы по одному и тому же основанию.
И после этого «отбрасываем» логарифмы! При этом, если основание степени , знак неравенства остается тем же. Если основание такое, что знак неравенства меняется на противоположный.
Конечно, мы не просто «отбрасываем» логарифмы. Мы пользуемся свойством монотонности логарифмической функции. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает, и тогда большему значению х соответствует большее значение выражения .
Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. Большему значению аргумента х будет соответствовать меньшее значение
Важное замечание: лучше всего записывать решение в виде цепочки равносильных переходов.
Перейдем к практике. Как всегда, начнем с самых простых неравенств.
1. Рассмотрим неравенство log3x > log35.
Поскольку логарифмы определены только для положительных чисел, необходимо, чтобы x был положительным. Условие x > 0 называется областью допустимых значений (ОДЗ) данного неравенства. Только при таких x неравенство имеет смысл.
Что делать дальше? Стандартный ответ, который дают школьники, — «Отбросить логарифмы!»
Что ж, эта формулировка лихо звучит и легко запоминается. Но почему мы все-таки можем это сделать?
Мы люди, мы обладаем интеллектом. Наш разум устроен так, что все логичное, понятное, имеющее внутреннюю структуру запоминается и применяется намного лучше, чем случайные и не связанные между собой факты. Вот почему важно не механически вызубрить правила, как дрессированная собачка-математик, а действовать осознанно.
Так почему же мы все-таки «отбрасываем логарифмы»?
Ответ простой: если основание больше единицы (как в нашем случае), логарифмическая функция монотонно возрастает, значит, большему значению x соответствует большее значение y и из неравенства log3x1 > log3x2 следует, что x1 > x2. 
Обратите внимание, мы перешли к алгебраическому неравенству, и знак неравенства при этом — сохраняется.
Следующее логарифмическое неравенство тоже простое.
Начнём с области допустимых значений. Логарифмы определены только для положительных чисел, поэтому
Решая эту систему, получим: x > 0.
Теперь от логарифмического неравенства перейдем к алгебраическому — «отбросим» логарифмы. Поскольку основание логарифма больше единицы, знак неравенства при этом сохраняется.
А что же будет, если основание логарифма меньше единицы? Легко догадаться, что в этом случае при переходе к алгебраическому неравенству знак неравенства будет меняться.
3. 
Запишем ОДЗ. Выражения, от которых берутся логарифмы, должны быть положительно, то есть
Решая эту систему, получим: x > 4,5.
Поскольку , логарифмическая функция с основанием монотонно убывает. А это значит, что большему значению функции отвечает меньшее значение аргумента: 
И если , то
2x − 9 ≤ x.
Получим, что x ≤ 9.
Учитывая, что x > 4,5, запишем ответ:
В следующей задаче показательное неравенство сводится к квадратному. Так что тему «квадратные неравенства» рекомендуем повторить.
Теперь более сложные неравенства:
4. Решите неравенство
5. Решите неравенство
Если , то . Нам повезло! Мы знаем, что основание логарифма больше единицы для всех значений х, входящих в ОДЗ.
Обратите внимание, что сначала мы полностью решаем неравенство относительно новой переменной t. И только после этого возвращаемся к переменной x. Запомните это и не ошибайтесь на экзамене!
6.
Запомним правило: если в уравнении или неравенстве присутствуют корни, дроби или логарифмы — решение надо начинать с области допустимых значений. Поскольку основание логарифма должно быть положительно и не равно единице, получим систему условий:
Упростим эту систему:
Это область допустимых значений неравенства.
Мы видим, что переменная содержится в основании логарифма. Перейдем к постоянному основанию. Напомним, что
В данном случае удобно перейти к основанию 4.
Сделаем замену
Упростим неравенство и решим его методом интервалов:
Вернемся к переменной x:
Мы добавили условие x > 0 (из ОДЗ).
Ответ:
7. Следующая задача тоже решается с помощью метода интервалов
Как всегда, решение логарифмического неравенства начинаем с области допустимых значений. В данном случае
0″ src=»https://latex.codecogs.com/png.latex?%5Cfrac%3C2-3x%3E%3Cx%3E%3E0″ />Это условие обязательно должно выполняться, и к нему мы вернемся. Рассмотрим пока само неравенство. Запишем левую часть как логарифм по основанию 3:
Правую часть тоже можно записать как логарифм по основанию 3, а затем перейти к алгебраическому неравенству:
Видим, что условие 0″ src=»https://latex.codecogs.com/png.latex?%5Cfrac%3C2-3x%3E%3Cx%3E%3E0″ /> (то есть ОДЗ) теперь выполняется автоматически. Что ж, это упрощает решение неравенства.
Решаем неравенство методом интервалов:
Ответ:
Получилось? Что же, повышаем уровень сложности:
8. Решите неравенство:
Неравенство равносильно системе:
9. Решите неравенство:
Выражение 5 — x 2 навязчиво повторяется в условии задачи. А это значит, что можно сделать замену:
Поскольку показательная функция принимает только положительные значения, t > 0. Тогда
Неравенство примет вид:
Уже лучше. Найдем область допустимых значений неравенства. Мы уже сказали, что t > 0. Кроме того, ( t − 3) (5 9 · t − 1) > 0
Если это условие выполнено, то и частное будет положительным.
А еще выражение под логарифмом в правой части неравенства должно быть положительно, то есть (625 t − 2) 2 .
Это означает, что 625 t − 2 ≠ 0, то есть
Аккуратно запишем ОДЗ
и решим получившуюся систему, применяя метод интервалов.
Итак,
Ну что ж, полдела сделано — разобрались с ОДЗ. Решаем само неравенство. Сумму логарифмов в левой части представим как логарифм произведения:
«Отбросим» логарифмы. Знак неравенства сохраняется.
Перенесем все в левую часть и разложим по известной формуле разности квадратов:
0;» src=»https://latex.codecogs.com/png.latex?(t-3)%5E%3C2%3E-(625t-2)%5E%3C2%3E%3E0;» />
0;» src=»https://latex.codecogs.com/png.latex?(t-3-625t+2)(t-3+625t-2)%3E0;» />
0.» src=»https://latex.codecogs.com/png.latex?(-624t-1)(626t-5)%3E0.» /> 
Вспомним, что (это ОДЗ неравенства) и найдем пересечение полученных промежутков.
Получим, что
Вернемся к переменной x
Поскольку
9;» src=»https://latex.codecogs.com/gif.latex?x%5E%3C2%3E%3E&space;9;» /> 0″ src=»https://latex.codecogs.com/png.latex?(x-3)(x+3)%3E0″ />
Ответ:
10. Еще один прием, упрощающий решение логарифмических неравенств, — переход к постоянному основанию. Покажем, как использовать переход к другому основанию и обобщенный метод интервалов.
Воспользуемся формулой и перейдем к основанию 10:
Применим обобщенный метод интервалов. Выражение в левой части неравенства можно записать как функцию
Эта функция может менять знак в точках, где она равна нулю или не существует.
Выражение lg | x − 3| равно нулю, если | x − 3| = 1, то есть x = 4 или x = 2.
Выражение lg (| x| − 2) равно нулю, если | x| = 3, то есть в точках 3 и −3.
Отметим эти точки на числовой прямой, с учетом ОДЗ неравенства.
Найдем знак функции g(x) на каждом из промежутков, на которые эти точки разбивают область допустимых значений. Точно так же мы решали методом интервалов обычные рациональные неравенства.
Ответ:
11. А в следующей задаче спрятаны целых две ловушки для невнимательных абитуриентов.
Запишем ОДЗ:
0\ x+2neq 1\ 36+16x-x^>0\ xneq 18 endright. : : : : : : : : Leftrightarrow : : : : : left <beginx>-2\ xneq -1\ xin (-2;18) endright.» src=»https://latex.codecogs.com/png.latex?%5Cleft%5C%3C%5Cbegin%3Cmatrix%3E&space;x+2%3E0%5C%5C&space;x+2%5Cneq&space;1%5C%5C&space;36+16x-x%5E%3C2%3E%3E0%5C%5C&space;x%5Cneq&space;18&space;%5Cend%3Cmatrix%3E%5Cright.&space;%5C:&space;%5C:&space;%5C:&space;%5C:&space;%5C:&space;%5C:&space;%5C:&space;%5C:&space;%5CLeftrightarrow&space;%5C:&space;%5C:&space;%5C:&space;%5C:&space;%5C:&space;%5Cleft%5C%3C%5Cbegin%3Cmatrix%3E&space;x%3E-2%5C%5C&space;x%5Cneq&space;-1%5C%5C&space;x%5Cin&space;(-2;18)&space;%5Cend%3Cmatrix%3E%5Cright.» />
Итак, Это ОДЗ.
Обратите внимание, что .
Это пригодится вам при решении неравенства.
Упростим исходное неравенство:
Теперь главное – не спешить. Мы уже говорили, что задача непростая – в ней расставлены ловушки. В первую вы попадете, если напишете, что Ведь выражение в данном случае не имеет смысла, поскольку x x — 18) 2 =(18 — x) 2 . Тогда:
Вторая ловушка – попроще. Запись означает, что сначала надо вычислить логарифм, а потом возвести полученное выражение в квадрат. Поэтому:
Дальше – всё просто. Сделаем замену
Выражение в левой части этого неравенства не может быть отрицательным, поэтому t = 2. Тогда
— не удовлетворяет ОДЗ;
Мы рассмотрели основные приемы решения логарифмических неравенств — от простейших до сложных, которые решаются с помощью обобщенного метода интервалов. Однако есть еще один интересный метод, помогающий справиться и показательными, и с логарифмическими, и с многими другими видами неравенств. Это метод рационализации (замены множителя). О нем — в следующей статье.
Видео:Решение логарифмических уравнений. Вебинар | МатематикаСкачать
Логарифмические уравнения и неравенства
Логарифмическим уравнениям и неравенствам в вариантах ЕГЭ по математике посвящена задача C3. Научиться решать задания C3 из ЕГЭ по математике должен каждый ученик, если он хочет сдать предстоящий экзамен на «хорошо» или «отлично». В данной статье представлен краткий обзор часто встречающихся логарифмических уравнений и неравенств, а также основных методов их решения.
Итак, разберем сегодня несколько примеров логарифмических уравнений и неравенств, которые предлагались учащимся в вариантах ЕГЭ по математике прошлых лет. Но начнет с краткого изложение основных теоретических моментов, которые нам понадобятся для их решения.
Видео:ОДЗ для логарифмических уравненийСкачать
Логарифмическая функция
Определение
0,, ane 1 ]» title=»Rendered by QuickLaTeX.com»/>
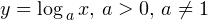
называют логарифмической функцией.
Основные свойства
Основные свойства логарифмической функции y = loga x:
| | a > 1 | 0 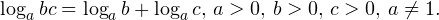 0,, b>0,, c>0,, ane 1. ]» title=»Rendered by QuickLaTeX.com»/>• Логарифм частного двух положительных чисел равен разности логарифмов этих чисел:
• Если a и b — положительные числа, причем a ≠ 1, то для любого числа r справедливо равенство:
• Если a, b, c — положительные числа, причем a и c отличны от единицы, то имеет место равенство (формула перехода к новому основанию логарифма):
Видео:Логарифмические уравнения. 11 класс.Скачать  Решение логарифмических уравнений и неравенствПример 1. Решите уравнение:
Решение. В область допустимых значений входят только те x, при которых выражение, находящееся под знаком логарифма, больше нуля. Эти значения определяются следующей системой неравенств:
С учетом того, что получаем промежуток, определяющий область допустимых значений данного логарифмического уравнения:
На основании теоремы 1, все условия которой здесь выполнены, переходим к следующему равносильному квадратичному уравнению:
В область допустимых значений входит только первый корень. Ответ: x = 7. Пример 2. Решите уравнение:
Решение. Область допустимых значений уравнения определяется системой неравенств:
Очевидно, что эти два условия противоречат друг другу. То есть нет ни одного такого значения x, при котором одновременно выполнялись бы оба неравенства. Область допустимых значений уравнения является пустым множеством, а значит решений у данного логарифмического уравнения нет. Ответ: корней нет. Обратите внимание, что в этом задании нам вообще не пришлось искать корни уравнения. Достаточно оказалось определить, что его область допустимых значений не содержит ни одного действительно числа. Это одно из преимуществ такой последовательности решения логарифмических уравнений и неравенств (начинать с определения области допустимых значений уравнения, а затем решать его путем равносильных преобразований). Примет 3. Решите уравнение:
Решение. Область допустимых значений уравнения определяется здесь легко: x > 0.
Уравнение принимает вид:
Оба ответа входят в область допустимых значений уравнения, поскольку являются положительными числами. Пример 4. Решите уравнение:
Решение. Вновь начнем решение с определения области допустимых значений уравнения. Она определяется следующей системой неравенств:
Воспользовавшись правилом сложения логарифмов, переходим к равносильному в области допустимых значений уравнению:
Основания логарифмов одинаковы, поэтому в области допустимых значений можно перейти к следующему квадратному уравнению:
Первый корень не входит в область допустимых значений уравнения, второй — входит. Ответ: x = -1. Пример 5. Решите уравнение:
Решение. Будем искать решения в промежутке x > 0, x≠1. Преобразуем уравнение к равносильному:
Оба ответа входят в область допустимых значений уравнения. Пример 6. Решите уравнение:
Решение. Система неравенств, определяющая область допустимых значений уравнения, имеет на этот раз вид: Используя свойства логарифма, преобразуем уравнение к равносильному в области допустимых значений уравнению:
Используя формулу перехода к новому основанию логарифма, получаем:
В область допустимых значений входит только один ответ: x = 4. Перейдем теперь к логарифмическим неравенствам. Это как раз то, с чем вам придется иметь дело на ЕГЭ по математике. Для решения дальнейших примеров нам потребуется следующая теорема: Теорема 2. Если f(x) > 0 и g(x) > 0, то: Решение. Начнем с определения области допустимых значений неравенства. Выражение, стоящее под знаком логарифмической функции, должно принимать только положительные значения. Это значит, что искомая область допустимых значений определяется следующей системой неравенств:
Так как в основании логарифма стоит число, меньшее единицы, соответствующая логарифмическая функция будет убывающей, а потому равносильным по теореме 2 будет переход к следующему квадратичному неравенству:
Окончательно, с учетом области допустимых значений получаем ответ:
Пример 8. Решите неравенство:
Решение. Вновь начнем с определения области допустимых значений:
На множестве допустимых значений неравенства проводим равносильные преобразования:
После сокращения и перехода к равносильному по теореме 2 неравенству получаем:
С учетом области допустимых значений получаем окончательный ответ:
Пример 9. Решите логарифмическое неравенство:
Решение. Область допустимых значений неравенства определяется следующей системой:
Видно, что в области допустимых значений выражение, стоящее в основании логарифма, всегда больше единицы, а потому равносильным по теореме 2 будет переход к следующему неравенству:
С учетом области допустимых значений получаем окончательный ответ:
Пример 10. Решите неравенство:
Решение. Область допустимых значений неравенства определяется системой неравенств:
I способ. Воспользуемся формулой перехода к новому основанию логарифма и перейдем к равносильному в области допустимых значений неравенству:
Неравенство будет равносильно двум системам. Первой:
Итак, окончательный ответ:
II способ. Решаем методом интервалов. Преобразуем неравенство к виду:
Вычтем из знаменателя
С учетом того, что выражения
Множество решений данного неравенства Итак, Итак, что нужно для того, чтобы решать логарифмические уравнения и неравенства?
Главное же требование — это настойчивость в достижении своей цели. Учитесь, тренируйтесь, если нужно — ежедневно, изучайте и запоминайте на примерах основные способы решения неравенств и их систем, анализируйте возникающие ошибки и не допускайте их в будущем. За помощью в этом нелегком деле вы можете обратиться к своему школьному учителю по математике, репетитору, родителям, друзьям и знакомым, книгам, а также огромному количеству материалов, доступных на просторах Интернета. Желаю вам успехов в подготовке к Единому государственному экзамену по математике. 📺 Видео11 класс, 17 урок, Логарифмические уравненияСкачать  ✓ Паника из-за ОДЗ | трушин ответит #018 | ЕГЭ. Задание 14. Математика. Профиль | Борис ТрушинСкачать  ОДЗ в логарифмических уравненияхСкачать  ЕГЭ база #7 / Логарифмические уравнения / Свойства, определение логарифма / решу егэСкачать  84 людей этого не знают! Секретный способ решения Логарифмических УравненийСкачать  Логарифмические неравенства. 11 класс.Скачать  ✓ Как решать логарифмические уравнения и неравенства, не помня свойства логарифмов | Борис ТрушинСкачать  Проще простого! Как решить Логарифмическое Уравнение?Скачать  Круговорот воды в природе ➜ Решение логарифмических уравнений из ЕГЭ #ShortsСкачать  Учёт ОДЗ в логарифмическом неравенствеСкачать  Старт Щелчка. №14 Неравенства с нуля и до ЕГЭ за 5 часов | Логарифмы, степени для №5,6,12Скачать  Логарифмические уравнения 🥷🏿Скачать  Логарифмы в ЕГЭ⚡️что получилось?!Скачать  Умножаем логарифмы В УМЕ🧠Скачать  |
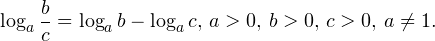0,, b>0,, c>0,, ane 1. ]» title=»Rendered by QuickLaTeX.com»/>
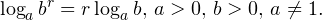0,, b>0,, ane 1. ]» title=»Rendered by QuickLaTeX.com»/>
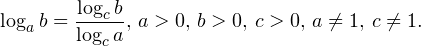0,, b>0,, c>0,, ane 1,, cne 1. ]» title=»Rendered by QuickLaTeX.com»/>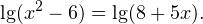
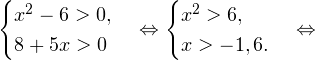0, \ 8+5x > 0 end Leftrightarrow begin x^2 > 6, \ x>-1,6. end Leftrightarrow ]» title=»Rendered by QuickLaTeX.com»/>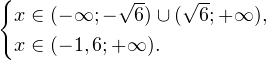
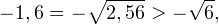-sqrt, ]» title=»Rendered by QuickLaTeX.com»/>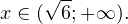
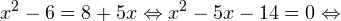
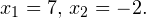
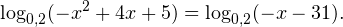
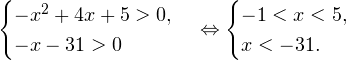0, \ -x-31>0 endLeftrightarrow begin -1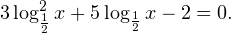
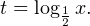
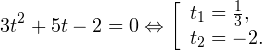
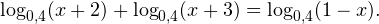
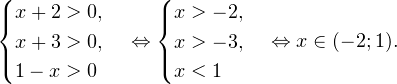0, \ x+3>0, \ 1-x>0 endLeftrightarrow begin x>-2, \ x>-3, \ x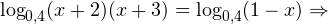
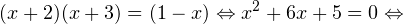
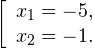
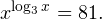
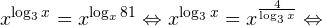
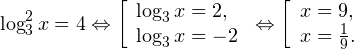
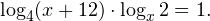
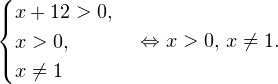0, \ x>0, \ xne 1 endLeftrightarrow x>0,, xne 1. ]» title=»Rendered by QuickLaTeX.com»/>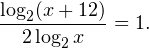
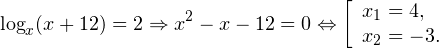
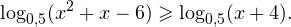
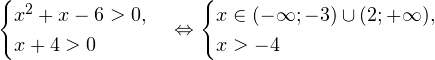0, \ x+4>0 endLeftrightarrow begin xin(-mathcal;-3)cup(2;+mathcal), \ x>-4 end ]» title=»Rendered by QuickLaTeX.com»/>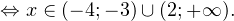
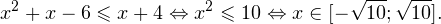
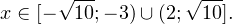
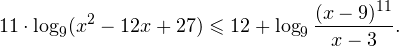
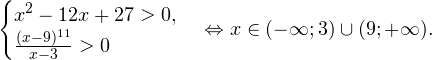0, \ frac<(x-9)^>>0 endLeftrightarrow xin(-mathcal;3)cup(9;+mathcal). ]» title=»Rendered by QuickLaTeX.com»/>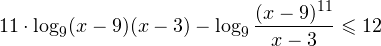
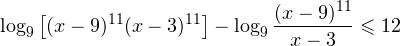
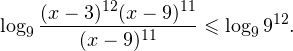
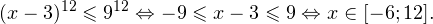
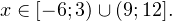
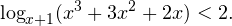
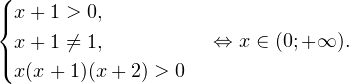0, \ x+1ne 1,\ x(x+1)(x+2)>0 endLeftrightarrow xin (0;+mathcal). ]» title=»Rendered by QuickLaTeX.com»/>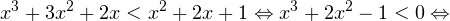
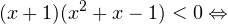
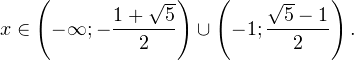
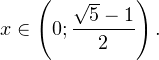
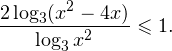
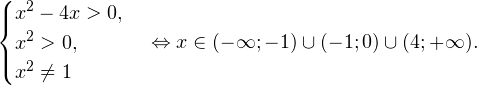0, \ x^2>0, \ x^2ne 1 endLeftrightarrow xin(-mathcal;-1)cup(-1;0)cup(4;+mathcal). ]» title=»Rendered by QuickLaTeX.com»/>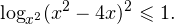
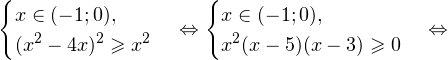
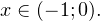
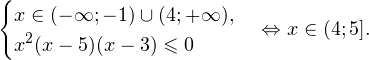
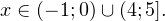
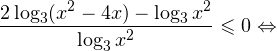
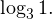Это ничего не изменит, поскольку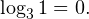 
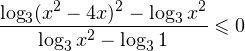
и 
— одного знака при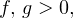 
0,» title=»Rendered by QuickLaTeX.com» height=»18″ width=»74″ style=»vertical-align: -4px;»/> в области допустимых значений имеет место следующий равносильный переход: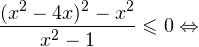
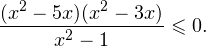
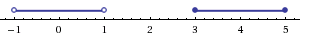
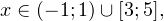а с учетом области допустимых значений получаем тот же результат: 