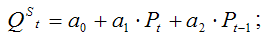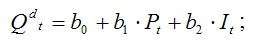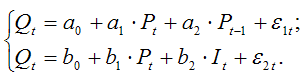Каким не может быть коэффициент корреляции?
2 . В каком случае выполняется соотношение для коэффициента детерминации и коэффициента корреляции 
?
a. в линейной модели;
b. в нелинейной модели;
c. как в линейной, так и в нелинейной
3. Оценки параметров модели называются эффективными, если:
a. математическое ожидание оценок параметров совпадает с истинными значениями этих параметров;
b. оценки параметров сходятся по вероятности к истинным значениям параметров;
c. в классе линейных оценок оценки параметров модели имеют минимальные дисперсии.
4.Коэффициент парной корреляции изменяется в пределах:
5. Оценку параметра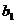 
парной линейной регрессии 
можно найти по формуле:
а) 
б) 
в) 
6. В регрессии: Y = 0, 1 + 4х тангенс угла наклона равен:
а) х б) y в) 4 г) 0,1
. 7.С учетом соотношения между заработной платой (в грн) –у и образованием (в годах) –х, у = 12,201 + 525 х, человек, который учился дополнительно один год, может ожидать такую дополнительную оплату: а)12,201 б)525 в)24,402 г)1,050
8. Критерий Стьюдента используется для оценки статистической значимости:
a. параметров модели;
b. коэффициента корреляции;
c. как параметров модели, так и коэффициента корреляции.
9. Коэффициент детерминации измеряет:
a. независимой переменной;
b. наклон линии регрессии;
c. всегда равен 1;
d. пересечение линии регрессии; д) общую вариацию независимой переменной, которая объясняется регрессией.
10. Значение выборочного коэффициента парной корреляции между факторами х и у определяется по формуле:
а.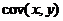 
b. 
c. 
11. Статистический анализ модели (статистическое оценивание ее параметров) относится к этапу:
- априорному;
- информационному;
- идентификации;
- верификации.
12. Линейные регрессионные модели, остатки которых не сохраняют постоянного уровня величины дисперсии при переходе от одного наблюдения к другому, называют моделями с:
a. гомоскедастичными остатками;
b. клонированными остатками;
c. гетероскдастичными остатками;
d. перпендикулярными остатками.
13. Временной ряд является нестационарным, если:
a. среднее значение его членов постоянно:
b. его случайная составляющая зависит от времени;
c. его члены не зависят от времени;
d. его неслучайная составляющая зависит от времени.
13. Теснота статистической связи между переменной и объясняющими переменными измеряется:
- моментом связи;
- коэффициентом детерминации;
- числом Блаттера;
- статистическим ансамблем.
14. Если регрессионные остатки в эконометрической модели статически взаимозависимы, то ее называют моделью с:
- автокоррелированными остатками;
- гомоскедастичными остатками;
- параллельными остатками;
- картезианскими остатками.
15. Линеаризация нелинейной модели регрессии может быть достигнута:
- отбрасыванием нелинейных переменных;
- перекрестной суперпозицией переменных;
- преобразованием анализируемых переменных;
- сглаживанием переменных.
Одно из условий идентифицируемости системы одновременных уравнений (СОУ) состоит в том, что
Видео:7inR 9. Structural models with testable identification (in Russian).Скачать
Эконометрика
Видео:Линейная алгебра. Алексей Савватеев и Александр Тонис. Лекция 14.2. Компактность: определениеСкачать
Список вопросов теста
Вопрос 1
Мера расхождения сглаженного (регрессионного) и наблюденного значения называется
Варианты ответов
- коэффициентом разности
- триангуляцией
- подвязкой
- невязкой
Вопрос 2
Временной ряд называется стационарным, если
Варианты ответов
- среднее значение членов ряда постоянно растет
- среднее значение членов ряда постоянно
- члены ряда образуют арифметическую прогрессию
- члены ряда образуют геометрическую прогрессию
Вопрос 3
Статистический анализ модели (статистическое оценивание ее параметров) относится к этапу
Варианты ответов
- идентификации
- верификации
- информационному
- априорному
Вопрос 4
Теснота статистической связи между переменной и объясняющими переменными измеряется
Варианты ответов
- статистическим ансамблем
- моментом связи
- коэффициентом детерминации
- числом Блаттера
Вопрос 5
Одним из известных способов проверки регрессионных остатков эконометрической модели на автокорреляцию является критерий
Варианты ответов
- Айзека-Азимова
- Дербина-Уотсона
- Куприна-Утрехта
- Марка-Шагала
Вопрос 6
Если регрессионные остатки в эконометрической модели статически взаимозависимы, то ее называют моделью с
Варианты ответов
- картезианскими остатками
- автокоррелированными остатками
- гомоскедастичными остатками
- параллельными остатками
Вопрос 7
Одно из условий идентифицируемости системы одновременных уравнений (СОУ) состоит в том, что
Варианты ответов
- число уравнений меньше числа анализируемых эндогенных переменных
- переменные являются коллинеарными
- переменные являются компланарными
- число уравнений равно числу анализируемых эндогенных переменных
Вопрос 8
Линейные регрессионные модели, остатки которых не сохраняют постоянного уровня величины дисперсии при переходе от одного наблюдения к другому, называют моделями с
Варианты ответов
- клонированными остатками
- гетероскдастичными остатками
- перпендикулярными остатками
- гомоскедастичными остатками
Вопрос 9
Линеаризация нелинейной модели регрессии может быть достигнута
Варианты ответов
- сглаживанием переменных
- перекрестной суперпозицией переменных
- отбрасыванием нелинейных переменных
- преобразованием анализируемых переменных
Вопрос 10
Линеаризация нелинейной модели регрессии может быть достигнута
Варианты ответов
- отбрасыванием нелинейных переменных
- сглаживанием переменных
- преобразованием анализируемых переменных
- перекрестной суперпозицией переменных
Вопрос 11
Одно из условий идентифицируемости системы одновременных уравнений (СОУ) состоит в том, что
Варианты ответов
- число уравнений меньше числа анализируемых эндогенных переменных
- переменные являются коллинеарными
- число уравнений равно числу анализируемых эндогенных переменных
- переменные являются компланарными
Вопрос 12
Временной ряд называется стационарным, если
Варианты ответов
- среднее значение членов ряда постоянно растет
- члены ряда образуют геометрическую прогрессию
- среднее значение членов ряда постоянно
- члены ряда образуют арифметическую прогрессию
Вопрос 13
Регрессионные модели с фиксированными переменными применяют, когда в ходе сбора исходных статистических данных имеет место
Варианты ответов
- верификационный спад
- суперактивная корреляция
- гомоскедастичное воздействие
- косвенное воздействие некоторых качественных факторов
Вопрос 14
Одним из известных способов проверки регрессионных остатков эконометрической модели на автокорреляцию является критерий
Варианты ответов
- Марка-Шагала
- Айзека-Азимова
- Куприна-Утрехта
- Дербина-Уотсона
Вопрос 15
Временной ряд является нестационарным, если
Варианты ответов
- его неслучайная составляющая зависит от времени
- его члены не зависят от времени
- его случайная составляющая зависит от времени
- среднее значение его членов постоянно
Вопрос 16
Регрессионные модели с фиксированными переменными применяют, когда в ходе сбора исходных статистических данных имеет место
Варианты ответов
- суперактивная корреляция
- гомоскедастичное воздействие
- косвенное воздействие некоторых качественных факторов
- верификационный спад
Вопрос 17
Временной ряд называется стационарным, если
Варианты ответов
- члены ряда образуют арифметическую прогрессию
- среднее значение членов ряда постоянно
- среднее значение членов ряда постоянно растет
- члены ряда образуют геометрическую прогрессию
Вопрос 18
Линейные регрессионные модели, остатки которых не сохраняют постоянного уровня величины дисперсии при переходе от одного наблюдения к другому, называют моделями с
Варианты ответов
- гомоскедастичными остатками
- гетероскдастичными остатками
- перпендикулярными остатками
- клонированными остатками
Вопрос 19
Форма записи эконометрической модели
B1 Y1 + B2 Y2 + C1 X = 1
B1 Y1 + B2 Y2 + C1 X = 1
Варианты ответов
- нормальной формой
- редуцированной формой
- структурной формой
- приведенной формой
Вопрос 20
Линеаризация нелинейной модели регрессии может быть достигнута
Варианты ответов
- преобразованием анализируемых переменных
- сглаживанием переменных
- перекрестной суперпозицией переменных
- отбрасыванием нелинейных переменных
Вопрос 21
Метод наименьших квадратов может применяться в случае
Варианты ответов
- только множественной регрессии
- нелинейной и линейной множественной регрессии
- коллинеарной регрессии
- только парной регрессии
Вопрос 22
Линейные регрессионные модели, остатки которых не сохраняют постоянного уровня величины дисперсии при переходе от одного наблюдения к другому, называют моделями
Варианты ответов
- с перпендикулярными остатками
- с гетероскдастичными остатками
- с гомоскедастичными остатками
- с клонированными остатками
Вопрос 23
Одно из условий идентифицируемости системы одновременных уравнений (СОУ) состоит в том, что
Варианты ответов
- переменные являются компланарными
- число уравнений равно числу анализируемых эндогенных переменных
- число уравнений меньше числа анализируемых эндогенных переменных
- переменные являются коллинеарными
Вопрос 24
Мера расхождения сглаженного (регрессионного) и наблюдаемого значения называется
Варианты ответов
- коэффициентом разности
- триангуляцией
- остатком
- подвязкой
Вопрос 25
Временной ряд является нестационарным, если
Варианты ответов
- его члены не зависят от времени
- его случайная составляющая зависит от времени
- его неслучайная составляющая зависит от времени
- среднее значение его членов постоянно
Вопрос 26
Теснота статистической связи между переменной и объясняющими переменными измеряется
Варианты ответов
- статистическим ансамблем
- моментом связи
- числом Блаттера
- коэффициентом детерминации
Вопрос 27
Регрессионные модели с фиксированными переменными применяют, когда в ходе сбора исходных статистических данных имеет место
Варианты ответов
- суперактивная корреляция
- косвенное воздействие некоторых качественных факторов
- гомоскедастичное воздействие
- верификационный спад
Вопрос 28
Внешние по отношению к рассматриваемой экономической модели переменные называются
Варианты ответов
- экзогенные
- лаговые
- эндогенные
- интерактивные
Вопрос 29
Теснота статистической связи между переменной и объясняющими переменными измеряется
Видео:Решение тригонометрических уравнений и их систем. 10 класс.Скачать
Условия идентификации структурной формы системы одновременных уравнений
Введём следующие обозначения:
N – количество предопределённых переменных структурной формы системы одновременных уравнений;
n – количество предопределённых переменных в уравнении, проверяемом на идентифицируемость;
M – количество эндогенных переменных структурной формы системы одновременных уравнений;
m – количество эндогенных переменных в уравнении, проверяемом на идентифицируемость;
K – матрица коэффициентов при переменных, не входящих в уравнение, проверяемое на идентифицируемость.
Необходимые и достаточные условия идентификации применяются только к структурной форме системы одновременных уравнений.
Первое необходимое условие идентифицируемости уравнения структурной формы системы одновременных уравнений.
Уравнение структурной формы системы одновременных уравнений идентифицируемо в том случае, если оно исключает хотя бы N-1 предопределённую переменную:
Второе необходимое условие идентифицируемости уравнения структурной формы системы одновременных уравнений.
Уравнение структурной формы системы одновременных уравнений идентифицируемо в том случае, если количество предопределённых переменных, не входящих в данное уравнение, будет не меньше числа эндогенных переменных этого уравнения минус единица:
Достаточное условие идентифицируемости уравнения структурной формы системы одновременных уравнений.
Уравнение структурной формы системы одновременных уравнений идентифицируемо в том случае, если ранг матрицы K равен (N-1).
Рангом матрицы называется размер наибольшей её квадратной подматрицы, определитель которой не равен нулю.
На основе перечисленных условий идентификации, можно сформулировать необходимые и достаточные условия идентифицируемости уравнения структурной формы системы одновременных уравнений:
- уравнение структурной формы системы одновременных уравнений считается сверхидентифицированным, если M–m>n–1 и ранг матрицы K равен (N-1);
- уравнение структурной формы системы одновременных уравнений считается точно идентифицированным, если M–m=n–1 и ранг матрицы K равен (N-1);
- уравнение структурной формы системы одновременных уравнений считается неидентифицированным, если M–m≥n–1 и ранг матрицы K меньше (N-1);
- уравнение структурной формы системы одновременных уравнений считается неидентифицированным, если M–m .
В качестве примера можно рассмотрим процесс идентификации структурной формы модели спроса и предложения. Данная модель включает в себя три уравнения:
1) уравнение предложения:
2) уравнение спроса:
3) тождество равновесия:
С учётом тождества равновесия, модель спроса-предложения может быть записана в виде:
Количество эндогенных переменных данной модели M равно двум (Pt и Qt), т.е. M=2. Количество предопределённых переменных данной модели N равно двум (Pt–1 и It), т.е. N=2.
Проверим выполнение первого необходимого условия идентифицируемости.
Для функции спроса выполняются равенства m=2 и n=1. Отсюда
следовательно, уравнение спроса является точно идентифицированным.
Для функции предложения выполняются равенства m=2 и n=1. Отсюда
следовательно, уравнение предложения является точно идентифицированным.
Проверим выполнение второго необходимого условия идентифицируемости.
Для функции спроса выполняются равенства m=2 и n=1. Отсюда
следовательно, уравнение спроса является точно идентифицированным.
Для функции предложения выполняются равенства m=2 и n=1. Отсюда
следовательно, уравнение предложения является точно идентифицированным.
Проверим выполнение достаточного условия идентифицируемости, заключающееся в том, чтобы хотя бы один из коэффициентов матрицы K не был равен нулю, т.к. M–1=1.
В первом уравнении модели исключена переменная It и матрица K=[b2]. Т.к. определитель данной матрицы не равен нулю, следовательно, rank=1=M–1 и уравнение является идентифицированным.
Во втором уравнении исключена переменная Pt–1 и матрица К=[a2]. Т.к. определитель данной матрицы не равен нулю, следовательно, rank=1=M–1 и уравнение является идентифицированным.
Т.к. уравнения спроса и предложения являются точно идентифицированными, то и система уравнений в целом точно идентифицирована.
Приведённая форма системы уравнений модели спроса-предложения:
📸 Видео
Математика базовая и математика углубленная: методика обучения решению уравненийСкачать
ЭконометрикаСкачать
Metrics, 2021-03-05, class IPСкачать
Коэффициент детерминации. Основы эконометрикиСкачать
Консультация к устному экзамену. Механика. Часть 10: "Основы теории относительности"Скачать
46. Вычисление пределов с помощью эквивалентных бесконечно малых функцийСкачать
Наука и Сон: Рентгеновские системыСкачать
Эконометрика. Построение модели множественной регрессии в Excel. Часть 1.Скачать
Модели представлений простых алгебр Ли классических серий и системы гипергеометрических уравненийСкачать
ЕГЭ. Физика. Промежуточный срез №7 «Повторение и обобщение» по пройденным темамСкачать
Урок 2. Часть 1. Eviews. Анализ временных рядов.Скачать
Как спрос и предложение задают ценыСкачать
СЛММ Арефьев Н.Г. A Theory of data-oriented identification with a SVAR applicationСкачать
