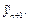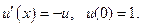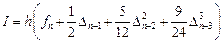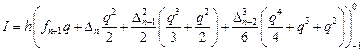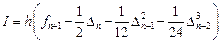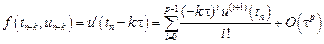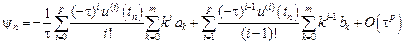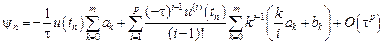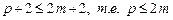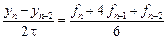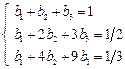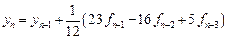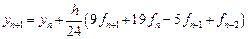Многошаговые методы
Решения задачи коши
9.1. Метод “предиктор-корректор” 2
9.2. Общая формулировка многошаговых методов 4
9.3. Устойчивость и сходимость разностных методов 7
9.1. Метод “предиктор-корректор”
В одношаговых методах значение yn+1 определяется лишь значениями tn, yn и значением шага приращения аргумента h. В многошаговых методах используется также информация в предыдущих точках yn-1, yn-2,
Многошаговые методы строятся на равномерной сетке
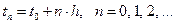
Обозначим: 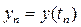
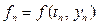
Линейный m-шаговый метод можно описать формулой:

Многошаговые методы не являются самостартующими. Для использования m-шагового метода необходимо предварительно задать m предыдущих значений y. Однако после того как многошаговый метод стартует, он работает быстрее, чем одношаговый. Например, при использовании метода Рунге-Кутта-Фельберга на каждом шаге приращения аргумента требуется шесть раз вычислять правую часть дифференциального уравнения 
Еще одним ограничением использования многошаговых методов является наличие равномерной сетки. Однако это ограничение легко преодолевается, например, с помощью интерполяции.
Многошаговые методы используются при решении жестких уравнений.
Порядок многошагового метода может выбираться автоматически и динамически изменяться.
Если 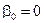
Если 
Частным случаем многошаговых методов являются методы Адамса:
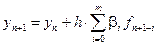
Методы Адамса также могут быть явными и неявными.
Трудности использования неявной формулы преодолевается в методе Предиктор–Корректор. В этом методе значение неизвестной функции в каждой точке сетки вычисляется дважды. Сначала вычисляется новое значение неизвестной функции 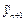

Простейшим примером метода Предиктор–Корректор является второй модифицированный метод Эйлера, который можно описать с помощью последовательности формул:

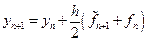
Метод Эйлера является одношаговым методом. Для построения многошаговых методов вновь используем утверждение: решение задачи Коши эквивалентно решению интегрального уравнения
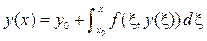
Для приближенного решения задачи Коши аппроксимируем подынтегральную функцию в формуле (9.3) с помощью интерполяционного многочлена. Интерполяционный многочлен Ньютона степени m для интерполирования назад от точки xn можно записать следующим образом

В формуле (9.4) 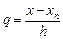

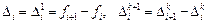

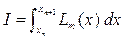
Найдем вначале формулы для двухшагового метода m=2. В качестве подынтегральной функции в формуле (9.6) будем использовать интерполяционный многочлен Ньютона первой степени.
Для вывода формулы предиктор вычислим интеграл (9.6) на отрезке экстраполяции 

и 
Подставив найденное значение интеграла в формулу (9.3), получим экстраполяционную формулу – формулу предиктор:

При выводе формулы корректор используем многочлен Ньютона для интерполирования от точки xn+1. Соответственно, в формуле (9.7) все индексы нужно увеличить на 1, а пределы интегрирования изменить на 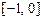
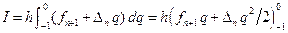
Подставив найденное значение интеграла в формулу (9.3), получим интерполяционную формулу – формулу корректор:
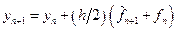
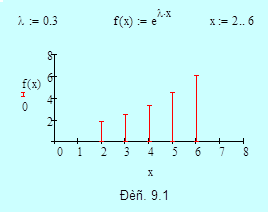
С помощью двухшагового метода предиктор-корректор найдем решение начальной задачи:
Точное решение представляет собой экспоненту 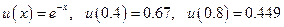
Выберем шаг приращения 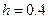
Начальное условие: 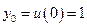
Дополнительное условие: 
С помощью формул (9.8) и (9.10) вычислим значение 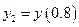
По формуле предиктор получаем: 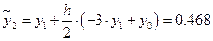
По формуле корректор уточняем решение: 
Для сравнения приведем расчеты значения 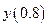

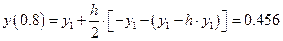
На практике обычно применяется четырехшаговый метод Адамса. Найдем формулы для четырехшагового метода. Повторяем весь ход рассуждений, использованных при выводе формул 2-шагового метода, но в отличие от предыдущего используем теперь многочлен Ньютона третьей степени.
Вывод формулы предиктор.
Подставив найденное значение интеграла в формулу (9.3), получим с учетом выражений (9.5) для конечных разностей формулу предиктор – формулу Адамса-Башфорта (Adams-Bashforth):
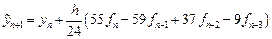
Вывод формулы корректор.
Аналогично предыдущему с учетом (9.3) и (9.5) получим формулу корректор – формулу Адамса-Мультона (Adams-Moulton):
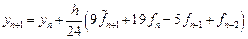
Общая формулировка многошаговых методов
Для решения задачи Коши
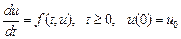
введем сетку с постоянным шагом 

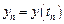

Линейным m-шаговым разностным методом называется система разностных уравнений
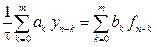
где 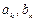
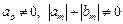
Уравнение (9.14) представляет собой рекуррентное соотношение, выражающее новое значение 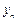
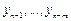
Заметим, что коэффициенты уравнения (9.14) определены с точностью до множителя. Для устранения неоднозначности будем считать, что выполнено условие нормировки

Метод называется явным, если 
Если 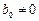
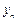

Это уравнение можно решить методом Ньютона, в качестве начального приближения взяв 
Погрешностью аппроксимации на решении или невязкой разностного метода (9.14) называется функция
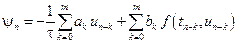
Функция невязки получается в результате подстановки точного решения дифференциального уравнения в разностное уравнение (9.14).
Подставим эти разложения в формулу для невязки
Изменим порядок суммирования. При этом во второй сумме будем суммировать по индексу i от 1 до p, соответственно уменьшив всюду индекс i на единицу.
Объединим суммы, выделив в первой сумме отдельно слагаемое с j=0.
Отсюда следует, что погрешность метода будет иметь порядок p, если выполнены условия:
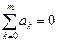
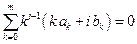

Заметим что, если в системе (9.17) отбросить последние s уравнений, то порядок метода понизится на s.
Итак, получили систему уравнений для коэффициентов ak, bk. К этим уравнениям нужно добавить еще условие нормировки (9.15): 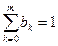
Для неявного метода имеем 2m+2 неизвестных: 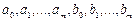
– для неявного метода порядок аппроксимации не превышает 2m.
Для явного метода имеем 2m+1 неизвестных: 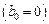
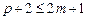
Преобразуем систему уравнений для коэффициентов ak, bk. С учетом условия нормировки уравнение 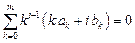
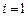
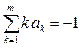
Окончательно получаем систему уравнений для коэффициентов линейного m-шагового разностного метода общего вида:
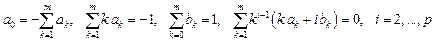
На практике часто используются методы Адамса, которые описываются формулой
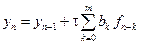
Для методов Адамса в системе (9.18) остаются только уравнения, определяющие коэффициенты bk.

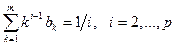
Имеем p уравнений. В случае неявного метода Адамса имеется m+1 неизвестных: 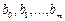
Рассмотрим варианты двухшаговых методов m=2. Максимальный порядок двухшагового метода равен p=4, так что можно написать следующую систему уравнений.
Ограничившись первыми четырьмя уравнениями этой системы, можно построить методы 2-го порядка. Если использовать пять уравнений, получим методы 3-го порядка. Система из шести уравнений определяет единственный двухшаговый метод 4-го порядка.
Варианты методов второго порядка.
1) Положим 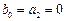
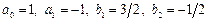

2) Положив 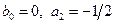

3) Положив 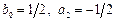
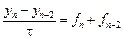
Варианты методов третьего порядка.
1) Положив 
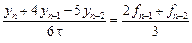
2) Если выбрать 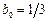

3) Выбрав 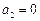
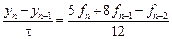
Метод четвертого порядка получим, используя все шесть уравнений:
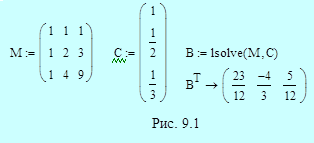
Явный трехшаговый метод имеет порядок p=3. В соответствии с формулами (9.20) для нахождения коэффициентов bk имеем систему уравнений, включающую условие нормировки и еще два уравнения для двух значений i: 
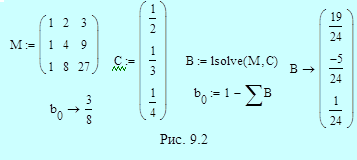
Неявный метод имеет четвертый порядок, и для коэффициентов 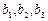
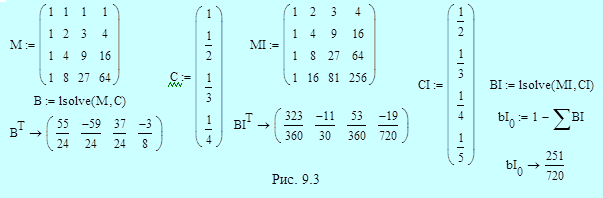 |
Пример 9.4. На рис. 9.3 приведено решение системы уравнений для коэффициентов явного и неявного четырехшаговых методов Адамса. Решение аналогично решению в примере 9.2 для трехшаговых методов. Обозначения M, C и B относятся к явному методу; обозначения MI, CI, BI и bI0 используются для описания неявного метода. Получаем в итоге:
- явный метод четвертого порядка (формула Адамса-Башфорта)
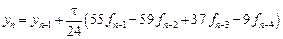
- неявный метод пятого порядка
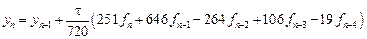
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Общая формулировка многошаговых методов
Многошаговые методы
Решения задачи коши
9.1. Метод “предиктор-корректор” 2
9.2. Общая формулировка многошаговых методов 4
9.3. Устойчивость и сходимость разностных методов 7
9.1. Метод “предиктор-корректор”
В одношаговых методах значение yn+1 определяется лишь значениями tn, yn и значением шага приращения аргумента h. В многошаговых методах используется также информация в предыдущих точках yn-1, yn-2,
Многошаговые методы строятся на равномерной сетке
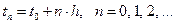
Обозначим: 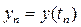
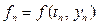
Линейный m-шаговый метод можно описать формулой:

Многошаговые методы не являются самостартующими. Для использования m-шагового метода необходимо предварительно задать m предыдущих значений y. Однако после того как многошаговый метод стартует, он работает быстрее, чем одношаговый. Например, при использовании метода Рунге-Кутта-Фельберга на каждом шаге приращения аргумента требуется шесть раз вычислять правую часть дифференциального уравнения 
Еще одним ограничением использования многошаговых методов является наличие равномерной сетки. Однако это ограничение легко преодолевается, например, с помощью интерполяции.
Многошаговые методы используются при решении жестких уравнений.
Порядок многошагового метода может выбираться автоматически и динамически изменяться.
Если 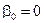
Если 
Частным случаем многошаговых методов являются методы Адамса:
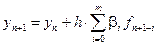
Методы Адамса также могут быть явными и неявными.
Трудности использования неявной формулы преодолевается в методе Предиктор–Корректор. В этом методе значение неизвестной функции в каждой точке сетки вычисляется дважды. Сначала вычисляется новое значение неизвестной функции 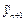

Простейшим примером метода Предиктор–Корректор является второй модифицированный метод Эйлера, который можно описать с помощью последовательности формул:

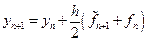
Метод Эйлера является одношаговым методом. Для построения многошаговых методов вновь используем утверждение: решение задачи Коши эквивалентно решению интегрального уравнения
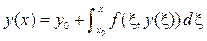
Для приближенного решения задачи Коши аппроксимируем подынтегральную функцию в формуле (9.3) с помощью интерполяционного многочлена. Интерполяционный многочлен Ньютона степени m для интерполирования назад от точки xn можно записать следующим образом

В формуле (9.4) 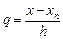

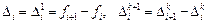

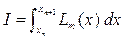
Найдем вначале формулы для двухшагового метода m=2. В качестве подынтегральной функции в формуле (9.6) будем использовать интерполяционный многочлен Ньютона первой степени.
Для вывода формулы предиктор вычислим интеграл (9.6) на отрезке экстраполяции 

и 
Подставив найденное значение интеграла в формулу (9.3), получим экстраполяционную формулу – формулу предиктор:

При выводе формулы корректор используем многочлен Ньютона для интерполирования от точки xn+1. Соответственно, в формуле (9.7) все индексы нужно увеличить на 1, а пределы интегрирования изменить на 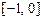
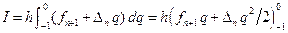
Подставив найденное значение интеграла в формулу (9.3), получим интерполяционную формулу – формулу корректор:
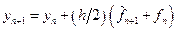
С помощью двухшагового метода предиктор-корректор найдем решение начальной задачи:
Точное решение представляет собой экспоненту 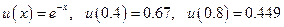
Выберем шаг приращения 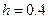
Начальное условие: 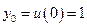
Дополнительное условие: 
С помощью формул (9.8) и (9.10) вычислим значение 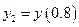
По формуле предиктор получаем: 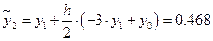
По формуле корректор уточняем решение: 
Для сравнения приведем расчеты значения 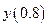

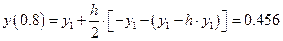
На практике обычно применяется четырехшаговый метод Адамса. Найдем формулы для четырехшагового метода. Повторяем весь ход рассуждений, использованных при выводе формул 2-шагового метода, но в отличие от предыдущего используем теперь многочлен Ньютона третьей степени.
Вывод формулы предиктор.
Подставив найденное значение интеграла в формулу (9.3), получим с учетом выражений (9.5) для конечных разностей формулу предиктор – формулу Адамса-Башфорта (Adams-Bashforth):
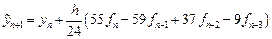
Вывод формулы корректор.
Аналогично предыдущему с учетом (9.3) и (9.5) получим формулу корректор – формулу Адамса-Мультона (Adams-Moulton):
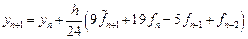
Общая формулировка многошаговых методов
Для решения задачи Коши
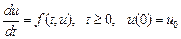
введем сетку с постоянным шагом 

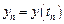

Линейным m-шаговым разностным методом называется система разностных уравнений
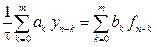
где 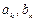
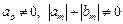
Уравнение (9.14) представляет собой рекуррентное соотношение, выражающее новое значение 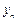
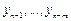
Заметим, что коэффициенты уравнения (9.14) определены с точностью до множителя. Для устранения неоднозначности будем считать, что выполнено условие нормировки

Метод называется явным, если 
Если 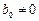
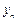

Это уравнение можно решить методом Ньютона, в качестве начального приближения взяв 
Погрешностью аппроксимации на решении или невязкой разностного метода (9.14) называется функция
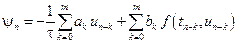
Функция невязки получается в результате подстановки точного решения дифференциального уравнения в разностное уравнение (9.14).
Подставим эти разложения в формулу для невязки
Изменим порядок суммирования. При этом во второй сумме будем суммировать по индексу i от 1 до p, соответственно уменьшив всюду индекс i на единицу.
Объединим суммы, выделив в первой сумме отдельно слагаемое с j=0.
Отсюда следует, что погрешность метода будет иметь порядок p, если выполнены условия:
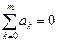
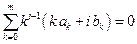

Заметим что, если в системе (9.17) отбросить последние s уравнений, то порядок метода понизится на s.
Итак, получили систему уравнений для коэффициентов ak, bk. К этим уравнениям нужно добавить еще условие нормировки (9.15): 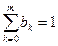
Для неявного метода имеем 2m+2 неизвестных: 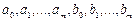
– для неявного метода порядок аппроксимации не превышает 2m.
Для явного метода имеем 2m+1 неизвестных: 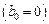
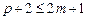
Преобразуем систему уравнений для коэффициентов ak, bk. С учетом условия нормировки уравнение 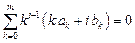
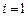
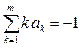
Окончательно получаем систему уравнений для коэффициентов линейного m-шагового разностного метода общего вида:
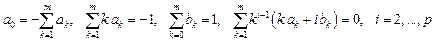
На практике часто используются методы Адамса, которые описываются формулой
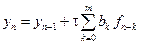
Для методов Адамса в системе (9.18) остаются только уравнения, определяющие коэффициенты bk.

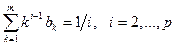
Имеем p уравнений. В случае неявного метода Адамса имеется m+1 неизвестных: 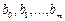
Рассмотрим варианты двухшаговых методов m=2. Максимальный порядок двухшагового метода равен p=4, так что можно написать следующую систему уравнений.
Ограничившись первыми четырьмя уравнениями этой системы, можно построить методы 2-го порядка. Если использовать пять уравнений, получим методы 3-го порядка. Система из шести уравнений определяет единственный двухшаговый метод 4-го порядка.
Варианты методов второго порядка.
1) Положим 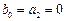
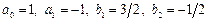

2) Положив 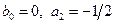

3) Положив 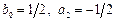
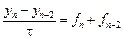
Варианты методов третьего порядка.
1) Положив 
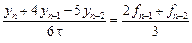
2) Если выбрать 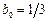

3) Выбрав 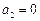
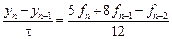
Метод четвертого порядка получим, используя все шесть уравнений:

Явный трехшаговый метод имеет порядок p=3. В соответствии с формулами (9.20) для нахождения коэффициентов bk имеем систему уравнений, включающую условие нормировки и еще два уравнения для двух значений i: 
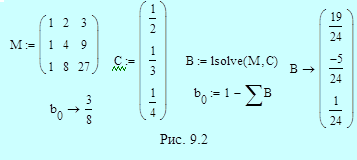
Неявный метод имеет четвертый порядок, и для коэффициентов 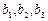
 |
Пример 9.4. На рис. 9.3 приведено решение системы уравнений для коэффициентов явного и неявного четырехшаговых методов Адамса. Решение аналогично решению в примере 9.2 для трехшаговых методов. Обозначения M, C и B относятся к явному методу; обозначения MI, CI, BI и bI0 используются для описания неявного метода. Получаем в итоге:
- явный метод четвертого порядка (формула Адамса-Башфорта)
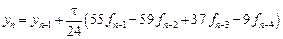
- неявный метод пятого порядка
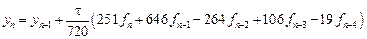
Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
При решении научных и инженерно-технических задач часто бывает необходимо математически описать какую-либо динамическую систему. Лучше всего это делать в виде дифференциальных уравнений (ДУ) или системы дифференциальных уравнений. Наиболее часто они такая задача возникает при решении проблем, связанных с моделированием кинетики химических реакций и различных явлений переноса (тепла, массы, импульса) – теплообмена, перемешивания, сушки, адсорбции, при описании движения макро- и микрочастиц.
Обыкновенным дифференциальным уравнением (ОДУ) n-го порядка называется следующее уравнение, которое содержит одну или несколько производных от искомой функции y(x):

В ряде случаев дифференциальное уравнение можно преобразовать к виду, в котором старшая производная выражена в явном виде. Такая форма записи называется уравнением, разрешенным относительно старшей производной (при этом в правой части уравнения старшая производная отсутствует):

Именно такая форма записи принята в качестве стандартной при рассмотрении численных методов решения ОДУ.
Линейным дифференциальным уравнением называется уравнение, линейное относительно функции y(x) и всех ее производных.
Например, ниже приведены линейные ОДУ первого и второго порядков
Решением обыкновенного дифференциального уравнения называется такая функция y(x), которая при любых х удовлетворяет этому уравнению в определенном конечном или бесконечном интервале. Процесс решения дифференциального уравнения называют интегрированием дифференциального уравнения.
Общее решение ОДУ n -го порядка содержит n произвольных констант C1 , C2 , …, Cn
Это очевидно следует из того, что неопределенный интеграл равен первообразной подынтегрального выражения плюс константа интегрирования
Так как для решения ДУ n -го порядка необходимо провести n интегрирований, то в общем решении появляется n констант интегрирования.
Частное решение ОДУ получается из общего, если константам интегрирования придать некоторые значения, определив некоторые дополнительные условия, количество которых позволяет вычислить все неопределенные константы интегрирования.
Точное (аналитическое) решение (общее или частное) дифференциального уравнения подразумевает получение искомого решения (функции y(x)) в виде выражения от элементарных функций. Это возможно далеко не всегда даже для уравнений первого порядка.
Численное решение ДУ (частное) заключается в вычислении функции y(x) и ее производных в некоторых заданных точках 
Например, для дифференциального уравнения первого порядка таблица решения будет представлять собой два столбца – x и y .
Множество значений абсцисс 


Для определения частного решения необходимо задать дополнительные условия, которые позволят вычислить константы интегрирования. Причем таких условий должно быть ровно n . Для уравнений первого порядка – одно, для второго — 2 и т.д. В зависимости от способа их задания при решении дифференциальных уравнений существуют три типа задач:
· Задача Коши (начальная задача): Необходимо найти такое частное решение дифференциального уравнения, которое удовлетворяет определенным начальными условиям, заданным в одной точке:
то есть, задано определенное значение независимой переменной (х0) , и значение функции и всех ее производных вплоть до порядка (n-1) в этой точке. Эта точка (х0) называется начальной. Например, если решается ДУ 1-го порядка, то начальные условия выражаются в виде пары чисел (x0, y0)
Такого рода задача встречается при решении ОДУ, которые описывают, например, кинетику химических реакций. В этом случае известны концентрации веществ в начальный момент времени (t = 0) , и необходимо найти концентрации веществ через некоторый промежуток времени (t) . В качестве примера можно так же привести задачу о теплопереносе или массопереносе (диффузии), уравнение движения материальной точки под действием сил и т.д.
· Краевая задача. В этом случае известны значения функции и (или) ее производных в более чем одной точке, например, в начальный и конечный момент времени, и необходимо найти частное решение дифференциального уравнения между этими точками. Сами дополнительные условия в этом случае называются краевыми (граничными) условиями. Естественно, что краевая задача может решаться для ОДУ не ниже 2-го порядка. Ниже приведен пример ОДУ второго порядка с граничными условиями (заданы значения функции в двух различных точках):
· Задача Штурма-Лиувиля (задача на собственные значения). Задачи этого типа похожи на краевую задачу. При их решении необходимо найти, при каких значениях какого-либо параметра решение ДУ удовлетворяет краевым условиям (собственные значения) и функции, которые являются решением ДУ при каждом значении параметра (собственные функции). Например, многие задачи квантовой механики являются задачами на собственные значения.
Численные методы решения задачи Коши ОДУ первого порядка
Рассмотрим некоторые численные методы решения задачи Коши (начальной задачи) обыкновенных дифференциальных уравнений первого порядка. Запишем данное уравнение в общем виде, разрешенном относительно производной (правая часть уравнения не зависит от первой производной):

Необходимо найти значения функции y в заданных точках сетки 


Преобразуем уравнение умножением на d x
И проинтегрируем левую и правую части между i -ым и i+ 1-ым узлами сетки.

Мы получили выражение для построения решения в i+1 узле интегрирования через значения x и y в i -ом узле сетки. Сложность, однако, заключается в том, что интеграл в правой части есть интеграл от неявно заданной функции, нахождение которого в аналитическом виде в общем случае невозможно. Численные методы решения ОДУ различным способом аппроксимируют (приближают) значение этого интеграла для построения формул численного интегрирования ОДУ.
Из множества разработанных для решения ОДУ первого порядка методов рассмотрим методы Эйлера, Рунге-Кутта и прогноза и коррекции. Они достаточно просты и дают начальное представление о подходах к решению данной задачи в рамках численного решения задачи Коши.
Исторически первым и наиболее простым способом численного решения задачи Коши для ОДУ первого порядка является метод Эйлера. В его основе лежит аппроксимация производной отношением конечных приращений зависимой (y) и независимой (x ) переменных между узлами равномерной сетки:
где yi+1 это искомое значение функции в точке xi+1 .
Если теперь преобразовать это уравнение, и учесть равномерность сетки интегрирования, то получится итерационная формула, по которой можно вычислить yi+1 , если известно yi в точке хi :

Сравнивая формулу Эйлера с общим выражением, полученным ранее, видно, что для приближенного вычисления интеграла в (6.3) в методе Эйлера используется простейшая формула интегрирования — формула прямоугольников по левому краю отрезка.
Графическая интерпретация метода Эйлера также не представляет затруднений (см. рисунок ниже). Действительно, исходя из вида решаемого уравнения (6.2) следует, что значение 

Из прямоугольного треугольника на рисунке можно найти

откуда и получается формула Эйлера. Таким образом, суть метода Эйлера заключается в замене функции y(x) на отрезке интегрирования прямой линией, касательной к графику в точке x=xi . Если искомая функция сильно отличается от линейной на отрезке интегрирования, то погрешность вычисления будет значительной. Ошибка метода Эйлера прямо пропорциональна шагу интегрирования:
Процесс вычислений строится следующим образом. При заданных начальных условиях x0 и y0 можно вычислить
Таким образом, строится таблица значений функции y(x) с определенным шагом (h) по x на отрезке [x0, xN]. Ошибка в определении значения y(xi) при этом будет тем меньше, чем меньше выбрана длина шага h (что определяется точностью формулы интегрирования).
При больших h метод Эйлера весьма неточен. Он дает все более точное приближение при уменьшении шага интегрирования. Если отрезок [xi, xi+1] слишком велик, то каждый участок [xi, xi+1] разбивается на N отрезков интегрирования и к каждому их них применяется формула Эйлера с шагом 
Используя метод Эйлера, построить приближенное решение для следующей задачи Коши:

Данное уравнение уже записано в стандартном виде, резрешенном относительно производной искомой функции.
Поэтому, для решаемого уравнения имеем
Примем шаг интегрирования равным шагу сетки h = 0,1. При этом для каждого узла сетки будет вычислено только одно значение ( N=1 ). Для первых четырех узлов сетки вычисления будут следующими:
Полные результаты (с точностью до пятого знака после запятой) приведены в таблице 1 в третьей колонке — h =0,1 ( N =1). Во второй колонке таблицы для сравнения приведены значения, вычисленные по аналитическому решению данного уравнения 
Во второй части таблицы приведена относительная погрешность полученных решений. Видно, что при h =0,1 погрешность весьма велика, достигая 100% для первого узла x =0,1.
Таблица 1 Решение уравнения (6.5) методом Эйлера (для колонок указан шаг интегрирования и число отрезков интегрирования N между узлами сетки)
| x | Точное решение | 0,1 | 0,05 | 0,025 | 0,00625 | 0,0015625 | 0,0007813 | 0,0001953 |
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 4 | 16 | 64 | 128 | 512 | ||
| 0 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 |
| 0,1 | 0,004837 | 0,000000 | 0,002500 | 0,003688 | 0,004554 | 0,004767 | 0,004802 | 0,004829 |
| 0,2 | 0,018731 | 0,010000 | 0,014506 | 0,016652 | 0,018217 | 0,018603 | 0,018667 | 0,018715 |
| 0,3 | 0,040818 | 0,029000 | 0,035092 | 0,037998 | 0,040121 | 0,040644 | 0,040731 | 0,040797 |
| 0,4 | 0,070320 | 0,056100 | 0,063420 | 0,066920 | 0,069479 | 0,070110 | 0,070215 | 0,070294 |
| 0,5 | 0,106531 | 0,090490 | 0,098737 | 0,102688 | 0,105580 | 0,106294 | 0,106412 | 0,106501 |
| 0,6 | 0,148812 | 0,131441 | 0,140360 | 0,144642 | 0,147779 | 0,148554 | 0,148683 | 0,148779 |
| 0,7 | 0,196585 | 0,178297 | 0,187675 | 0,192186 | 0,195496 | 0,196314 | 0,196449 | 0,196551 |
| 0,8 | 0,249329 | 0,230467 | 0,240127 | 0,244783 | 0,248202 | 0,249048 | 0,249188 | 0,249294 |
| 0,9 | 0,306570 | 0,287420 | 0,297214 | 0,301945 | 0,305423 | 0,306284 | 0,306427 | 0,306534 |
| 1 | 0,367879 | 0,348678 | 0,358486 | 0,363232 | 0,366727 | 0,367592 | 0,367736 | 0,367844 |
| x | h | 0,1 | 0,05 | 0,025 | 0,00625 | 0,0015625 | 0,0007813 | 0,0001953 |
| N | 1 | 2 | 4 | 16 | 64 | 128 | 512 | |
| 0,1 | 100,00% | 48,32% | 23,76% | 5,87% | 1,46% | 0,73% | 0,18% | |
| 0,2 | 46,61% | 22,55% | 11,10% | 2,74% | 0,68% | 0,34% | 0,09% | |
| 0,3 | 28,95% | 14,03% | 6,91% | 1,71% | 0,43% | 0,21% | 0,05% | |
| 0,4 | 20,22% | 9,81% | 4,83% | 1,20% | 0,30% | 0,15% | 0,04% | |
| 0,5 | 15,06% | 7,32% | 3,61% | 0,89% | 0,22% | 0,11% | 0,03% | |
| 0,6 | 11,67% | 5,68% | 2,80% | 0,69% | 0,17% | 0,09% | 0,02% | |
| 0,7 | 9,30% | 4,53% | 2,24% | 0,55% | 0,14% | 0,07% | 0,02% | |
| 0,8 | 7,57% | 3,69% | 1,82% | 0,45% | 0,11% | 0,06% | 0,01% | |
| 0,9 | 6,25% | 3,05% | 1,51% | 0,37% | 0,09% | 0,05% | 0,01% | |
| 1 | 5,22% | 2,55% | 1,26% | 0,31% | 0,08% | 0,04% | 0,01% |
Уменьшим шаг интегрирования вдвое, h = 0.05, в этом случае для каждого узла сетки вычисление будет проводиться за два шага ( N =2). Так, для первого узла x =0,1 получим:
И так далее, до конца отрезка.
Из таблицы 1 (четвертая колонка, N =2) видно, что погрешность решения резко снизилась, примерно вдвое, хотя и осталась по-прежнему, значительной.
При шаге интегрирования h =0,025 для каждого узла сетки необходимо выполнить 4 вычисления по формуле Эйлера в промежуточных точках ( N =4).
(Для других узлов значения приведены в таблице 1, колонка N =4)
В таблице 1 приведены для сравнения вычисления для некоторых других значений N , вплоть до 512. Видно, что точность решения возрастает весьма медленно при уменьшении шага интегрирования, необходимо брать очень маленький шаг для достижения приемлемой точности (и, следовательно, много раз вычислять значение F(x,y)) . Поэтому метод Эйлера практически не используется в вычислительной практике.
Усовершенствованный метод Эйлера. Метод Гюна.
Точность метода Эйлера можно повысить, если воспользоваться для аппроксимации интеграла более точной формулой интегрирования – формулой трапеций.

Данная формула оказывается неявной относительно yi+1 (это значение есть и в левой и в правой части выражения), то есть является уравением относительно yi+1 , решать которое можно, например, численно, применяя какой-либо итерационный метод (в таком виде его можно рассматривать как итерационную формула метода простой итерации). Однако, можно поступить иначи и приблизительно вычислить значение функции в узле i+1 с помощью обычной формулы Эйлера:

которое затем использовать при вычислении по (6.6).
Таким образом получается метод Гюна или метод Эйлера с пересчетом. Для каждого узла интегрирования производится следующая цепочка вычислений

Благодаря более точной формуле интегрирования, погрешность метода Гюна пропорциональна уже квадрату шага интегрирования.
Подход, использованный в методе Гюна, используется для построения так называемых методов прогноза и коррекции, которые будут рассмотрены позже.
Проведем вычисления для уравения (6.5) с помощью метода Гюна.
При шаге интегрирования h =0,1 в первом узле сетки x1 получим:
Что намного точнее значения, полученного методом Эйлера при том же шаге интегрирования. В таблице 2 ниже приведены сравнительные результаты вычислений при h = 0,1 методов Эйлера и Гюна.
Таблица 2 Решение уравнения методами Эйлера и Гюна
| x | Точное | Метод Гюна | Метод Эйлера | ||
|---|---|---|---|---|---|
| y | отн. погрешность | y | отн. погрешность | ||
| 0 | 0,000000 | 0,00000 | 0,00000 | ||
| 0,1 | 0,004837 | 0,00500 | 3,36% | 0,00000 | 100,00% |
| 0,2 | 0,018731 | 0,01903 | 1,57% | 0,01000 | 46,61% |
| 0,3 | 0,040818 | 0,04122 | 0,98% | 0,02900 | 28,95% |
| 0,4 | 0,070320 | 0,07080 | 0,69% | 0,05610 | 20,22% |
| 0,5 | 0,106531 | 0,10708 | 0,51% | 0,09049 | 15,06% |
| 0,6 | 0,148812 | 0,14940 | 0,40% | 0,13144 | 11,67% |
| 0,7 | 0,196585 | 0,19721 | 0,32% | 0,17830 | 9,30% |
| 0,8 | 0,249329 | 0,24998 | 0,26% | 0,23047 | 7,57% |
| 0,9 | 0,306570 | 0,30723 | 0,21% | 0,28742 | 6,25% |
| 1 | 0,367879 | 0,36854 | 0,18% | 0,34868 | 5,22% |
Отметим существенное увеличение точности вычислений метода Гюна по сравнению с методом Эйлера. Так, для узла x =0,1 относительное отклонение значения функции, определенного методом Гюна, оказывается в 30 (!) раз меньше. Такая же точность вычислений по формуле Эйлера достигается при числе отрезков интегрирования N примерно 30. Следовательно, при использовании метода Гюна при одинаковой точности вычислений понадобится примерно в 15 раз меньше времени ЭВМ, чем при использовании метода Эйлера.
Проверка устойчивости решения
Решение ОДУ в некоторой точке xi называется устойчивым, если найденное в этой точке значение функции yi мало изменяется при уменьшении шага интегрирования. Для проверки устойчивости, таким образом, надо провести два расчета значения (yi) – с шагом интегрирования h и при уменьшенной (например, двое) величине шага
В качестве критерия устойчивости можно использовать малость относительного изменения полученного решения при уменьшении шага интегрирования ( ε – наперед заданная малая величина)
Такая проверка может осуществляться и для всех решений на всем интервале значений x. Если условие не выполняется, то шаг снова делится пополам и находится новое решение и т.д. до получения устойчивого решения.
Дальнейшее улучшение точности решения ОДУ первого порядка возможно за счет увеличения точности приближенного вычисления интеграла в выражении (6.3).
Мы уже видели, какое преимущество дает переход от интегрирования по формуле прямоугольников (метод Эйлера) к использованию формулы трапеций (метод Гюна) при аппроксимации этого интеграла.
Воспользовавшись хорошо зарекомендовавшей себя формулой Симпсона, можно получить еще более точную формулу для решения задачи Коши для ОДУ первого порядка — широко используемого в вычислительной практике метода Рунге-Кутты.
В формуле Симпсона для приближенного вычисления определенного интеграла используются значения подинтегрального выражения в трех точках. В интеграле их всего две, поэтому введем дополнительную точку в середине отрезка [ xi+1 xi ]
тогда можно переписать так:
Полученное выражение является неявным, так как в правой части содержатся еще не определенные значения функции yi+h/2 и yi+1 . Чтобы воспользоваться этой формулой, надо использовать некоторое приближение для вычисления этих значений
При использовании различных методов приближенного вычисления этих величин, получаются выражения для методов Рунге-Кутты различного порядка точности.
Алгоритм Рунге-Кутты третьего порядка — РК3 (погрешность порядка h 3 ):

Алгоритм Рунге-Кутты четвертого порядка- РК4 (погрешность порядка h 4 ):

Алгоритмы третьего и четвертого порядков требуют на каждом шаге трех и четырех вычислений функции соответственно, но являются весьма точными.
Используя алгоритм Рунге-Кутты третьего (6.8) и четвертого (6.9) порядков решить задачу (6.5) с шагом h =0.1:
Для алгоритма третьего порядка (для узла x =0.1) вычисления таковы:
Для алгоритма четвертого порядка (для узла x =0.1) вычисления таковы:
Приведем таблицу решения с шагом интегрирования h =0,1 методов Рунге-Кутты 3-го (РК3) и четвертого (РК4) порядков на интегрвале [0,1] и их относительные отклонения от точного решения.
| x | РК3 | РК4 | ||
|---|---|---|---|---|
| y | отн.погр. | y | отн.погр. | |
| 0 | 0 | 0 | ||
| 0,1 | 0,00483333 | 0,08444% | 0,0048375 | 0,00169% |
| 0,2 | 0,01872336 | 0,03946% | 0,0187309 | 0,00079% |
| 0,3 | 0,04080819 | 0,02458% | 0,04081842 | 0,00049% |
| 0,4 | 0,07030794 | 0,01721% | 0,07032029 | 0,00035% |
| 0,5 | 0,10651697 | 0,01285% | 0,10653093 | 0,00026% |
| 0,6 | 0,14879677 | 0,00999% | 0,14881193 | 0,00020% |
| 0,7 | 0,19656961 | 0,00798% | 0,19658562 | 0,00016% |
| 0,8 | 0,24931274 | 0,00651% | 0,24932929 | 0,00013% |
| 0,9 | 0,30655314 | 0,00539% | 0,30656999 | 0,00011% |
| 1 | 0,36786283 | 0,00451% | 0,36787977 | 0,00009% |
Как видно, точность решения, полученного методом Рунге-Кутты четвертого порядка, намного превышает точность решения, полученного методом Гюна и методом Рунге-Кутты 3-го порядка (сравнте с данными Таблицы 2). При шаге h = 0,1 он позволил точно определить четыре значащие цифры решения, тогда как для достижения такой точности с помощью метода Эйлера необходимо взять h = 0,0001, что требует более тысячи (. ) вычислений функции F(x,y ). При шаге h = 0,05 точность решения в этом узле достигает шести значащих цифр.
Высокая точность, вместе с достаточной простотой реализации делает метод Рунге-Кутты четвертого порядка одним из весьма распространенных численных методов решения задачи Коши ОДУ и систем ОДУ первого порядка.
Рассмотренные ранее методы (Эйлера, Гюна, Рунге-Кутты) используют значение функции на одном предшествующем шаге, поэтому они относятся к так называемым одношаговым методам. Точность вычислений можно увеличить, если использовать при нахождении решения в некотором узле xi информацию о значениях функции, полученных в нескольких ( k ) предыдущих узлах сетки интегрирования (xi-1, xi-2 … xi-k ).
Если используются значения в k предыдущих узлах, то говорят о k-шаговом методе интегрирования уравнения. Одним из способов построения многошаговых методов заключается в следующем. По значениям функции, вычисленным в k предшествующих узлах, строится интерполяционный полином степени (k-1) — 

где λl – квадратурные коэффициенты.
Очевидно, что при k =1 в качестве частного случая получается уже известная нам формула Эйлера. Значения квадратурных коэффициентов для k от 2 до 4 приведены в таблице.
| k | λl | |||
|---|---|---|---|---|
| 2 | 3/2 | -1/2 | ||
| 3 | 23/12 | -16/12 | 5/12 | |
| 4 | 55/24 | -59/24 | 37/24 | -9/24 |
Полученное таким образом семейство формул называется явной k -шаговой схемой Адамса (методы Адамса-Башфорта).
Например, четырехшаговая явная формула Адамса может быть записана так:
Если для построения интерполяционного полинома использовать k узлов, начиная с xi+1, то можно получить формулы интегрирования ОДУ, известные как неявные схемы Адамса (или методы Адамса-Моултона). Неявными эти формулы называются потому, что значение искомой функции в (i+1)-м узле — yi+1 — оказывается одновременно и в левой и правой частях равенства.
Квадратурные коэффициенты для неявных методов Адамса приведены в таблице ниже.
| k | λl | |||
|---|---|---|---|---|
| 2 | 1/2 | 1/2 | ||
| 3 | 5/12 | 8/12 | -1/12 | |
| 4 | 9/24 | 19/24 | -5/24 | 1/24 |
Например, четырехшаговая неявная формула Адамса-Моултона имеет вид:
Видно, что это выражение является уравнением относительно yi+1, так как yi+1 встречается и в левой и правой его части. Однако обычно это уравнение не решается, а значение в правой части заменяется на рассчитанное по какой-либо явной формуле — например, формуле Адамса-Башфорта. Такой подход лежит в основе методов «прогноза-коррекции».
Достоинством многошаговых методов Адамса при решении ОДУ заключается в том, что в каждом узле рассчитывается только одно значение правой части ОДУ — функции F(x,y ). К недостаткам можно отнести невозможность старта многошагового метода из единственной начальной точки, так как для вычислений по k -шаговой формуле необходимо знание значения функции в k узлах. Поэтому приходится (k-1) решение в первых узлах x1, x2, …, xk-1 получать с помощью какого-либо одношагового метода, например метода Рунге-Кутты 4–го порядка.
Другой проблемой является невозможность изменения шага в процессе решения, что легко реализуется в одношаговых методах.
Методы прогноза и коррекции
Несколько иной подход используется в многошаговых методах прогноза и коррекции. В качестве иллюстрирующего примера рассмотрим 2-х шаговый метод прогноза и коррекции.
Пусть дано ДУ для которого известно значение функции в двух соседних узлах сетки:
Сначала строится прогноз значения в (i+1) -ом узле интегрирования по какой-либо грубой формуле (при k =2 это метод Эйлера) по предудущему узлу.
Затем это значение корректируется по более точной формуле, в данном случае – по формуле трапеций (неявная формула Адамса второго порядка)
В качестве решения в узле xi+1 
где Ec — ошибка коррекции
Для того чтобы начать расчет методом прогноза и коррекции, необходимо знать значения функции в двух первых узлах сетки — x0 и x1 — 
На каждом шаге построения решения методом прогноза и коррекции требуется вычислить всего одно значение функции, а одно берется из предыдущего узла сетки. Поэтому он весьма экономичен по затратам времени вычислений при достаточной точности.
Погрешность описываемого метода пропорциональна h 3 (d
Аналогичные схемы прогноза-коррекции могут быть получены сочетанием явных (прогноз) и неявных (коррекция) формул Адамса для различных k. Так, например, широко применяется четырехшаговый метод прогноза-коррекции, в котором в качестве прогноза используется 4-х шаговая формула Адамса-Башфорта, а для коррекции — 4-х шаговая формула Адамса-Моултона. Погрешность такого метода пропорциональна
С использованием алгоритма прогноза и коррекции второго порядка решить ДУ в точке x2 = 0,2 при h = 0,1 со следующими начальными значениями:
При h = 0,1 получаем
Аналитическое решение уравнения (с точностью до 9 знака после запятой) дает значение
y (0,2) =0,018730753. Относительная погрешность составляет 0,049%.
Решение задачи Коши для систем дифференциальных уравнений 1-го порядка
Системой M дифференциальных уравнений первого порядка в общем случае можно назвать следующую совокупность Обыкновенных дифференциальных уравнений:

Где 
Начальными условиями при решения задачи Коши для такой системы будут являться значение независимой переменной и значения всех M функций при этом значении:
Все описанные ранее методы решения задачи Коши для уравнений легко обобщаются на случай решения систем ДУ первого порядка. Формулы выбранного метода применяются последовательно к каждому уравнению системы уравнений для определения значения соответствующей функции. Из первого уравнения определяется значение y 1 i , из второго – y 2 i , …, из M -го — yMi .
В качестве примера рассмотрим применение метода Рунге-Кутты 4-го порядка для решения системы двух ОДУ первого порядка.
Адаптируем формулу Рунге-Кутты 4-го порядка для данной системы уравнений. Из первого уравнения будем вычислять значения функции u(x), а из второго – функции v(x) (это функции, чьи производные стоят в левой части соотетствующих уравнений):
Аналогично для второго:
С учетом вышесказанного, для расчета коэффициентов ku0 — ku3 используем правую часть первого уравнения ( F 1), а для коэффициентов kv0 — kv3 — второго ( F2). Кроме этого, для расчета приращения функции u используем коэффициенты ku, а для расчета приращения функции v — kv. Таким образом, коэффициенты рассчитываются по следующим формулам:
Модель «хищник-жертва»
Примером задачи, сводимой к системе нелинейных дифференциальных уравнений 1-го порядка, является задача «хищник — жертва» (модель Лóтки-Вольтéрры). Данная модель довольно широко применяется при описании временной зависимости объема популяций в биологических системах, при моделировании экономических и физических процессов.
Задача формулируется следующим образом. Пусть в системе в некоторый момент времени t имеются хищники (например, волки) в количестве v ( t ) и жертвы (например, зайцы) в количестве u ( t ). Модель «хищник — жертва» утверждает, что u ( t ) и v ( t ) удовлетворяют системе ОДУ первого порядка:
Где A , B , C и D – некоторые числовые константы.
Действительно, если зайцы имеют достаточно травы для питания, то скорость роста популяции будет прямо пропорциональна их числу (первое слагаемое в первом уравнении). Второе слагаемое описывает гибель зайцев при встрече с хищниками, так как вероятность их встречи равна произведению 

Применим метод Рунге-Кутты 4-го порядка для решения полученной системы уравнений. Сравнивая решаемую систему и систему, записанную в стандартной форме, заметим, что:
Значения функций u и v находятся по уже известным формулам:
Решение задачи Коши для дифференциальных уравнений второго и более высоких порядков
Задачу Коши для ОДУ второго порядка

можно свести к решению системы двух ДУ первого порядка, если ввести некоторую функцию
тогда 

Аналогично, ОДУ порядка n сведется к системе из n дифференциальных уравнений первого порядка.
Движение тела под действием пружины
Рассмотрим некоторое материальное тело массой m , которое движется по горизонтальной поверхности (в общем случае – с трением) под действием пружины.
Сила упругого сжатия (растяжения) пружины описывается законом Гука и пропорциональна смещению тела от положения равновесия пружины ( x = 0):
k – коэффициент жесткости пружины.
Сила трения направлена всегда против движения тела и пропорциональна его скорости:
с – коэффициент трения.
Баланс сил, действующих на тело в каждый момент времени можно записать так:
С учетом того, что координата тела есть функция от времени, а скорость и ускорение – это первая и вторая производная координаты во времени, соответственно, получим:
Таким образом, изменение координаты тела от времени описывается ОДУ 2-го порядка, которое в стандартном виде записывается так:
Начальными условиями в данной задачи являются значения координаты тела и его скорости в начальный момент времени (t = 0):
Как было показано, ОДУ 2-го порядка сводится к системе двух уравнений 1-го порядка подстановкой:
Окончательно система ОДУ принимает вид:
с начальными условиями
Применим метод Рунге-Кутты 4-го порядка для решения полученной системы уравнений. Правые части уравненией имеют вид:
Из первого уравнения рассчитываем значения функции x ( t ), из второго – v ( t ).
Теперь запишем соответствующие выражения для расчета коэффициентов k x0 – k x3 и k v0 — k v3.
Решение других проблем, связанных с дифференциальными уравнениями – задачи с граничными условиями и задачи на собственные значения и функции в данном курсе не рассматриваются.
Химические задачи, сводящиеся к решению ДУ
Кинетика химических реакций
для которой k1 и k2 k3 — константы скорости реакций:
Решение системы из четырех ДУ зависит от начальных значений концентраций веществ
и от констант скоростей реакций k1, k2 и k3 .
📸 Видео
Решение обыкновенных дифференциальных уравнений. Часть 1Скачать

7.4 Многошаговые методыСкачать

5 Численное решение дифференциальных уравнений Part 1Скачать

Дифференциальные уравнения. 11 класс.Скачать

Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Численное решение задачи Коши методом ЭйлераСкачать

7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Решение системы дифференциальных уравнений методом ЭйлераСкачать

5 Численное решение дифференциальных уравнений Part 1Скачать

Метод ЭйлераСкачать

3_11. Алгоритм Рунге-КуттыСкачать

2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

4. Однородные дифференциальные уравнения (часть 1)Скачать

18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

Лабораторная работа 1. Решение систем обыкновенных дифференциальных уравненийСкачать

Дифференциальные уравнения. Задача Коши. Метод Эйлера.Скачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать