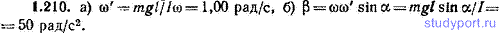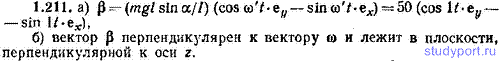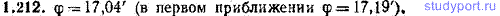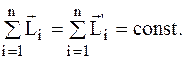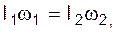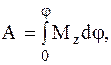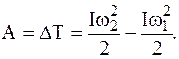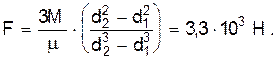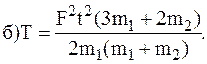1.207. Однородный цилиндр массы m и радиуса R вращается вокруг своей оси. Угловая скорость цилиндра изменяется за время t от значения ω1 до значения ω2. Какую среднюю мощность развивают силы, действующие на цилиндр?
1.208. Ротор некоторого агрегата снабжен дисковым тормозом. Этот тормоз состоит из двух дисков радиуса R = 150 мм, один из которых закреплен на конце оси ротора, а другой, лишенный возможности вращаться, может прижиматься к первому с силой F=100 Н. Тормоз включают в момент, когда ротор вращается по инерции со скоростью ω=50,0 рад/с (трением в подшипниках можно пренебречь). Момент инерции ротора вместе с укрепленным на нем диском тормоза I=0,628 кг*м 2 . Коэффициент трения между поверхностями дисков не зависит от их относительной скорости и равен k=0,250. Считая, что сила F равномерно распределяется по поверхности дисков, определить, сколько оборотов N успеет сделать ротор до остановки.
1.209. Гироскоп в виде однородного диска радиуса R=8,00 см вращается вокруг своей оси с угловой скоростью ω=3,00*10 2 рад/с. Угловая скорость прецессии гироскопа ω’=1,00 рад/с. Определить расстояние l от точки опоры до центра масс гироскопа. Моментом инерции оси гироскопа пренебречь.
1.210. Гироскоп массы m = 1,000 кг, имеющий момент инерции I=4,905*10 -3 кг*м 2 , вращается с угловой скоростью 100,0 рад/с. Расстояние от точки опоры до центра масс l=5,00 см. Угол между вертикалью и осью гироскопа α=30,0°. Найти: а) модуль угловой скорости прецессии ω’, б) модуль углового ускорения гироскопа β.
1.211. Поместив начало координат в точку опоры гироскопа и направив ось z вверх по вертикали, а) найти угловое ускорение β гироскопа из предыдущей задачи; считать, что в начальный момент ось гироскопа находилась в плоскости х, z; б) вычислив скалярное произведение ωβ, определить, как направлен вектор β.
1.212. Гироскоп, вращающийся вокруг оси симметрии с угловой скоростью ω=100 рад/с, прецессирует в поле земного тяготения с угловой скоростью ω’=1,00 рад/с. Угол между вертикалью и осью гироскопа α = 30,0°. Определить угол φ между осью симметрии и направлением угловой скорости гироскопа Ω (см. задачу 1.49). Решить задачу методом последовательных приближений, положив φ в нулевом приближении равным нулю.
Ошибка в тексте? Выдели её мышкой и нажми 
Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!
Видео:Видеоурок по математике "Цилиндр"Скачать
системы от времени t, если движение началось в момент времени t Однородный диск массы m и радиуса R раскрутили вокруг его оси до
1 6.1. Однородный цилиндр массы M и радиуса R может вращаться без трения вокруг горизонтальной оси. На цилиндр намотана нить, к концу которой прикреплен груз массы m. Найти зависимость кинетической энергии всей системы от времени t, если движение началось в момент времени t Однородный диск массы m и радиуса R раскрутили вокруг его оси до угловой скорости ω и осторожно положили плашмя на стол. Коэффициент трения диска о стол μ. Сколько оборотов N сделает диск до полной остановки? 6.3. Гладкий тонкий однородный стержень АВ массы M и длины L в горизонтальной плоскости свободно вращается с угловой скоростью ω 0 вокруг неподвижной вертикальной оси, проходящей через начало А стержня. Небольшая муфточка массы m, расположенная в точке А стержня, начинает скользить вдоль стержня по направлению к его концу В. Какую скорость V относительно стержня приобретет муфточка в момент достижения конца B? 6.4. Однородная тонкая квадратная пластинка со стороной L и массой M может свободно вращаться вокруг неподвижной вертикальной оси, совмещенной с одной из еѐ сторон. В центр покоящейся пластинки по нормали к ней упруго ударяется шарик массы m, летящий со скоростью V. Найти скорость u шарика после упругого удара. 1
2 6.5. Однородный диск массы M и радиуса R может свободно вращаться в горизонтальной плоскости вокруг неподвижной вертикальной оси, проходящей через центр диска. Человек массы m, стоящий на краю неподвижного диска, начинает двигаться вдоль края диска, совершает перемещение на угол φ относительно диска и останавливается. На какой угол θ поворачивается диск вокруг своей оси в результате перемещения человека? 6.6. Два параллельных горизонтальных диска 1 и 2 свободно вращаются вокруг вертикальной оси, проходящей через их центры. Моменты инерции дисков относительно этой оси равны J 1 и J 2, а угловые скорости дисков равны ω 1 и ω 2. Через некоторое время после падения верхнего диска на нижний вследствие силы трения между поверхностями дисков они оба вращаются как единое целое. Найти работу А, которую совершили силы трения Однородный диск радиуса R в положении 1 свободно вращается вокруг своей горизонтальной оси с угловой скоростью ω. В положении 2, после падения диска на шероховатую горизонтальную поверхность, он отскакивает от поверхности под углом θ, но уже не вращаясь. Какова скорость V диска сразу после отскока? 2
3 6.8. Однородный шар массы m скатывается без скольжения по наклонной плоскости, составляющей угол α с горизонтом. Найти кинетическую энергию шара через время t после начала движения Вертикально висящая тонкая однородная прямоугольная доска массы M и длины L может вращаться без трения вокруг горизонтальной оси, совмещенной с еѐ верхней короткой стороной. Пуля массы m, летящая горизонтально с начальной скоростью V в направлении, перпендикулярном к плоскости доски, пробивает доску в еѐ нижнем конце и далее снова летит горизонтально с меньшей скоростью u. Найти максимальный угол φ отклонения доски от вертикали Однородный тонкий тяжелый стержень длины l висит на горизонтальной оси, проходящей через один из его концов. Какую надо сообщить стержню начальную угловую скорость ω, чтобы он повернулся на угол φ 90? При вращении горизонтального однородного диска массы m 1 и радиуса R вокруг неподвижной вертикальной оси, проходящей через его центр, в оси возникает постоянный момент силы трения, равный M. Над покоящимся диском расположена горизонтальная круглая монета массы m 2 и радиуса r, геометрическая ось которой смещена на расстояние d от оси диска. Монета, раскрученная вокруг своей оси симметрии до угловой скорости ω, падает на покоящийся диск и мгновенно к нему прилипает. Сколько оборотов N сделает диск с прилипшей монетой до полной остановки системы? 3
4 6.12. Тонкий стержень массы m и длины L подвешен за один конец и может вращаться без трения вокруг горизонтальной оси O. К той же оси подвешен на нити длины l маленький шарик такой же массы m. Шарик отклоняют на некоторый угол и отпускают. Происходит абсолютно упругий удар шарика о стержень. При какой длине нити шарик после удара о стержень остановится? В общей точке подвеса А подвешены маленький шарик массы m на нити длины l и однородный стержень массы M и длины L, отклоненный в сторону на некоторый угол. При возвращении стержня в положение равновесия происходит упругий удар. Каким должно быть соотношение между массами стержня и шарика, чтобы после удара шарик и точка удара стержня стали двигаться с равными скоростями в противоположных направлениях? Стержень массы M и длины L, который может свободно вращаться вокруг неподвижной горизонтальной оси, проходящей через один из его концов, под действием силы тяжести переходит из горизонтального положения в вертикальное. Проходя через вертикальное положение, стержень нижним концом упруго ударяет о малое тело массы m, лежащее на гладком горизонтальном столе. Определить скорость V тела после удара. 4
5 6.15. Вертикальный столб высотой L подпиливают у его основания. Столб падает на землю, поворачиваясь вокруг нижнего основания. Определить линейную скорость V его верхнего конца в момент удара о землю Закрытая с торцов горизонтальная трубка АВ массы M имеет тонкую гладкую стенку, радиус которой пренебрежимо мал по сравнению с длиной L трубки. В середине трубки находится шарик массы m, привязанный нитью к торцу А трубки. Трубку с шариком раскрутили до угловой скорости ω вокруг неподвижной вертикальной оси, совмещенной с торцом А трубки, и отпустили. После обрыва нити шарик прилипает к торцу В трубки. Какой стала установившаяся угловая скорость системы после прилипания шарика? Закрытая с торцов горизонтальная трубка АВ массы M имеет тонкую гладкую стенку, радиус которой пренебрежимо мал по сравнению с длиной L трубки. В середине трубки находится шарик массы m, привязанный нитью к торцу А трубки. Трубку с шариком раскрутили до угловой скорости ω вокруг неподвижной вертикальной оси, совмещенной с торцом А трубки, и отпустили. После обрыва нити шарик прилипает к торцу В трубки. На какую величину изменилась кинетическая энергия системы? 5
6 6.18. Цепочка длины L и массы m, нанизанная на невесомый стержень АВ, свободно вращается в горизонтальной плоскости с угловой скоростью ω вокруг неподвижной вертикальной оси, проходящей через его середину. Цепочка разрывается точно посредине, и все звенья еѐ обеих половинок плотно прижимаются к упорам на концах стержня. На какую величину изменилась кинетическая энергия всех звеньев цепочки? Тонкий однородный стержень АВ массы m и длины L покоится на гладкой горизонтальной поверхности. В результате произведенного в горизонтальной плоскости перпендикулярного удара в некоторую точку стержня он получает импульс р. На каком расстоянии от конца А следует произвести удар, чтобы скорость точки А сразу же после удара равнялась нулю? Горизонтально расположенный диск массы M и радиуса R имеет радиальную направляющую с гладкими стенками. С помощью нити, пропущенной через полую вертикальную ось в центре диска и привязанной к маленькому шарику массы m, шарик можно подтягивать вдоль этой направляющей от края диска к его центру. Вначале диск с шариком на его краю раскрутили до угловой скорости ω вокруг неподвижной вертикальной оси в центре диска и 6
7 отпустили. Найти работу силы натяжения нити, совершаемую при медленном перемещении шарика от края к центру диска На гладкой горизонтальной плоскости покоится небольшая шайба и тонкий однородный стержень длины L. Масса стержня в n раз больше массы шайбы. Шайбе сообщают в горизонтальной плоскости скорость V, направленную перпендикулярно к стержню. Шайба испытывает упругое соударение с концом стержня. При каком значении n скорость шайбы после столкновения станет равной нулю? Тонкий однородный стержень массы M и длины L подвешен за один конец и может вращаться без трения вокруг горизонтальной оси. Пуля массы m m M, летящая горизонтально в плоскости вращения стержня, попадает в нижний конец стержня и застревает в нем. Стержень с пулей отклоняется на угол α. Какова была скорость V пули до попадания в стержень? Центр массивного однородного тонкого диска 1 радиуса R насажен на правый конец горизонтального тонкого и легкого стержня 2 длины L. Другой конец стержня шарнирно закреплен в верхней точке О неподвижной вертикальной стойки 3, где нет трения. Диск раскручен до большой угловой скорости ω вокруг оси симметрии. Под действием силы тяжести диск прецессирует с малой угловой скоростью Ω вокруг вертикальной оси стойки 3. Какова величина угловой скорости раскрученного диска ω? 7
8 6.24. Симметричный волчок массы m представляет собой сплошной однородный конус с круговым основанием радиуса R и вершиной O, которая совмещена с неподвижной точкой опоры волчка на горизонтальной поверхности. Расстояние от вершины O конуса до точки центра масс С равно L. Угловая скорость вращения волчка вокруг оси симметрии, которая наклонена под углом θ к вертикали, равна ω. Под действием силы тяжести волчок прецессирует. Найти величину и направление вектора угловой скорости прецессии волчка Корабль движется со скоростью V по дуге окружности радиуса R. Ось ротора турбины расположена вдоль корабля. Момент инерции ротора, вращающегося с угловой скоростью ω, равен J. Найти момент гироскопических сил, действующих со стороны ротора корабля на подшипники. 8
Видео:Вращательное движение. 10 класс.Скачать
Закон сохранения момента импульса
Для замкнутой (изолированной) системы материальных точек 
и ее момент импульса остается постоянным для n взаимодействующих материальных точек.
Для замкнутой системы, состоящей из n взаимодействующих тел с осью вращения, неподвижной в пространстве,
где Ii – момент импульса i-го тела относительно оси вращения z;
wzi – проекция угловой скорости i-го тела на ту же ось до взаимодействия, а помеченные штрихом – те же величины после взаимодействия.
Закон сохранения момента импульса для двух взаимодействующих тел относительно неподвижной оси
где I1, I2, w1, w2 – моменты инерции и угловые скорости тел до взаимодействия, а 
те же величины после взаимодействия.
Закон сохранения момента импульса для одного тела, момент инерции которого изменяется при взаимодействии
где индексом 1 и 2 помечены величины моментов импульсов и угловых скоростей до и после взаимодействия.
Работа и мощность момента силы
Работа, совершаемая внешней силой при вращении твердого тела, вокруг неподвижной оси
где Mz – проекция момента сил на неподвижную ось вращения; dj – элементарный угол поворота.
Работа постоянного момента силы M, вращающего тело вокруг неподвижной оси
где j – полный угол поворота тела.
Мгновенная мощность момента силы M, развиваемая при вращении вокруг неподвижной оси
где w – угловая скорость.
Кинетическая энергия вращательного движения
.
Кинетическая энергия тела, катящегося по плоскости:
,
где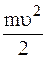 
– кинетическая энергия его поступательного движения, а 
– кинетическая энергия вращательного движения.
Связь работы с изменением вращательной кинетической энергии
Работа момента сил, действующего на тело, идет на приращение вращательной кинетической энергии тела
ВОПРОСЫ И УПРАЖНЕНИЯ
1. Исходя из основного закона динамики в форме 
, получите уравнение динамики вращательного движения для материальной точки 
.
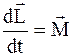
2. Дайте определение момента силы 
и момента импульса 
относительно: а) точки, б) оси вращения. Каковы свойства этих физических величин? Какие у них размерности?
3. Покажите, что для системы материальных точек 
, где 
– момент импульса системы, 
– результирующий момент внешних сил.
4. Сформулируйте закон сохранения момента импульса для системы материальных точек, указав на его связь с изотропностью пространства. Приведите примеры сохранения момента импульса.
5. Получите уравнение моментов для материальной точки, движущейся по окружности, относительно неподвижной оси вращения: Iez=Mz.
6. Чему равен момент инерции I материальной точки относительно оси вращения?
7. Запишите уравнение вращательного движения твердого тела вокруг неподвижной оси. Чему равен момент инерции I твердого тела относительно оси вращения? Является ли эта величина аддитивной?
8. Запишите и сформулируйте теорему Штейнера.
9. Приведите соотношения для моментов инерции однородных тел правильной геометрической формы.
10. Запишите выражение для кинетической энергии твердого тела, вращающегося вокруг неподвижной оси. Чему равна кинетическая энергия твердого тела при плоском движении?
11. Как определить работу внешних сил при вращении твердого тела вокруг неподвижной оси? Чему равна мощность при вращательном движении?
12. Как приращение вращательной кинетической энергии связано с работой момента силы?
ЗАДАЧИ ГРУППЫ А
1.(3.9) Маховое колесо, момент инерции которого I=245 кгм 2 , вращается с частотой n=20 об/c. Через время t=1 мин после того, как на колесо перестал действовать момент сил М, оно остановилось. Найти момент сил трения Мтр и число оборотов N, которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском.
Ответ: Мтр=513 Н×м; N=600 об.
2.(3.13) На барабан радиусом R=20 см, момент инерции которого I=0,1 кг×м 2 , намотан шнур, к концу которого привязан груз массой m=0,5 кг. До начала вращения барабана высота груза над полом h0=1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Ек груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь.
Ответ: t=1,1 c; Ek=0,81 Дж; T=4,1 H.
3.(3.14) Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I=50 кг×м 2 и радиус R=20 см. Момент сил трения вращающегося блока Мтр=98,1 Н×м. Найти разность сил натяжения нити Т1–Т2 по обе стороны блока, если известно, что блок вращается с угловым ускорением e=2,36 рад/c 2 . Блок считать однородным диском. Нить не проскальзывает.
4.(3.28) Найти линейные скорости u движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h=0,5 м, начальная скорость всех тел u0=0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения.
Ответ: u1=2,65 м/c, u2=2,56 м/c, u3=2,21 м/c; u=3,13 м/c.
5.(3.32)Маховое колесо, момент инерции которого I=245 кгм 2 , вращается с частотой n=20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N=1000 об. Найти момент сил трения Мтр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса.
Ответ: Мтр=308 Н×м; t=100 c.
6.(3.34) Маховое колесо начинает вращаться с угловым ускорением e=0,5 рад/c 2 и через время t1=15 с после начала движения приобретает момент импульса L=73,5 кг×м 2 /c. Найти кинетическую энергию T колеса через время t2=20 с после начала движения.
Ответ: T=490 Дж.
7.(3.36) К ободу диска массой m=5 кг приложена касательная сила F=19,6 Н. Какую кинетическую энергию T будет иметь диск через время t=5 с после начала действия силы?
Ответ: T= 1,92 кДж.
8.(3.38) Однородный стержень длиной l=85 см подвешен к горизонтальной оси, проходящей через верхний конец стержня. Какую скорость u надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси?
Ответ: u=7,1 м/c.
9.(3.40) Горизонтальная платформа массой m=100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой n1=10 об/мин. Человек массой m0=60 кг стоит при этом на краю платформы. С какой частотой n2 начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека — точечной массой. Трения в оси нет.
Ответ: n2=22 об/мин.
10.(3.42) Горизонтальная платформа массой m=80 кг и радиусом R=1 м вращается с частотой n1=20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой n2 будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от I1=2,94 кгм 2 до I2=0,98 кг×м 2 ? Считать платформу однородным диском. Трения нет.
Ответ: n2=21 об/мин.
11.(3.44) Человек массой m0=60 кг находится на неподвижной платформе массой m=100 кг. С какой частотой n будет вращаться платформа, если человек начнет движение по окружности радиусом r=5 м вокруг оси вращения? Скорость движения человека относительно платформы u0=4 км/ч. Радиус платформы R=10 м. Считать платформу однородным диском, а человека — точечной массой. Трения в оси нет.
Ответ: n=0,49 об/мин.
ЗАДАЧИ ГРУППЫ Б
1.(1.43) Однородный диск радиусом R=0,2 м вращается с постоянным угловым ускорением e=100 с -2 под действием силы F=100 Н, приложенной по касательной к его ободу. Определить массу m диска, если при вращении на него также действует постоянный момент силы трения Mтр=5 Н×м.
Ответ: m=7,5 кг.
2.(1.44) Однородный цилиндр начинает вращение с постоянным угловым ускорением e=0,3 с -2 и через t1=25 с после начала движения приобретает момент импульса L=75 кг×м 2 /с. Определить кинетическую энергию T цилиндра через t2=40 с после начала вращения.
Ответ: T=720 Дж.
3.(1.45) Диск массой m=0,8 кг и радиусом R=30 см вращается с частотой n=10 об/с. Под действием внешних сил диск останавливается. Найти работу A внешних сил.
Ответ: A=71 Дж.
4.(1.46) На обод маховика диаметром d=40 см намотан шнур, к концу которого привязан груз массой m=3 кг. Определить момент инерции I маховика, если он, вращаясь равноускоренно под действием груза, приобрел угловую скорость w=9 с -1 в течение t=3 с после начала движения.
Ответ: I=1,84 кгм 2 .
5.(1.49) Стержень массой m=2 кг и длиной l=1,2 м вращается вокруг оси, проходящей через его середину, согласно уравнению j=Аt+Bt 2 , (А=3 с -1 , В=0,2 с -2 ). Определить вращающий момент M, действующий на стержень.
Ответ: M=0,096 Н×м.
6.(1.50) Стержень массой m=6 кг и длиной l=1,2 м вращается в горизонтальной плоскости под действием силы F=10 Н, приложенной перпендикулярно к одному из его концов. Ось вращения вертикальна и проходит через второй конец стержня. Определить угловое ускорение e и частоту вращения n стержня через t=5 с после начала действия силы.
Ответ: e=4,17 с -2 , n=3,32 об/с.
7.(1.51) Мяч массой m=200 г пролетает в горизонтальном направлении на расстоянии r=0,5 м от оси вращения неподвижной скамьи Жуковского, в центре которой стоит человек. После того , как человек поймал мяч, скамья стала вращаться с угловой скоростью w=0,05 с -1 . Определить скорость пролета мяча u, если суммарный момент инерции человека и скамьи I=20 кг×м 2 . Трения в оси нет.
Ответ: u=10 м/с.
8.(1.53) В центре скамьи Жуковского стоит человек и держит в руках конец стержня. Стержень расположен вертикально вдоль оси вращения скамьи, которая вращается при этом с угловой скоростью w1=5 с -1 . Длина стержня l=1,6 м, его масса m=4 кг. Суммарный момент инерции человека и скамьи I=7,5 кг×м 2 . С какой угловой скоростью w2 будет вращаться скамья, если повернуть стержень так, чтобы он занял горизонтальное положение. Трения в оси нет.
Ответ: w2=3,42 с -1 .
9.(1.56) Платформа вращается вокруг вертикальной оси, проходящей через ее центр, с частотой n1=0,5 об/с. В центре ее стоит человек и держит на вытянутых руках гири массой m=5 кг каждая. С какой частотой n2 будет вращаться платформа, если человек сожмет руки и расстояние каждой гири от оси вращения уменьшится от r1=80 см до r2=25 см? Суммарный момент инерции человека и платформы относительно оси вращения I=2,4 кг×м 2 .
Ответ: n2=1,45 об/с.
10.(1.57) Стержень длиной l=1,2 м и массой M=5 кг может вращаться около горизонтальной оси, проходящей через его верхний конец. В нижний конец стержня попадает пуля массой m=20 г, летящая горизонтально со скоростью u=400 м/с, и застревает в нем. На какой угол j отклонится стержень после попадания пули?
Ответ: j=68,4 0 .
11.(1.58) Через отверстие в горизонтальной поверхности пропущена нить длиной l1=1,6 м. К другому концу нити прикреплен шарик массой m=50 г, который вращается с частотой n1=3 об/с, двигаясь по поверхности без трения. С какой частотой n2 будет вращаться шарик, если постепенно укоротить нить до длины l2=0,8 м. Какую работу A совершит при этом сила, укорачивающая нить? Трения нет.
Ответ: n2=12 об/с, A=67,2 Дж.
ЗАДАЧИ ГРУППЫ С
1. Вращение от двигателя к ведущим колесам автомобиля передается через ряд устройств, одно из которых, называемое сцеплением, позволяет в случае надобности отключить двигатель от остальных устройств. Сцепление, в принципе, состоит из двух одинаковых фрикционных накладок, прижимаемых друг к другу сильными пружинами. В автомобиле «Жигули» фрикционные накладки имеют форму колец с внутренним диаметром d1=142 мм и наружным диаметром d2=203 мм. Коэффициент трения накладки по накладке m=0,35. Найти наименьшую силу F, с которой нужно прижимать накладки, чтобы передать вращательный момент M=100 Н×м.
Ответ: 
2. Тонкий стержень длиной l=1 м и массой m=0,6 кг может вращаться без трения вокруг горизонтальной оси, перпендикулярной к нему, и отстоящей от центра стержня на расстояние а=0,1 м. Стержень приводится в горизонтальное положение и отпускается без толчка. Определить: а) угловое ускорение стержня e0 и силу давления F0 на ось в начальный момент времени; б) угловую скорость w и силу давления F на ось в момент прохождения стержнем положения равновесия.
Ответ: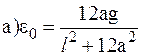 
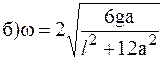
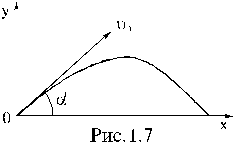=11 рад/с 2 ,
=5,3 Н=0,89 mg;
=4,6 рад/с,
=7,1 Н=1,21 mg.
 |
3. Тело массой m брошено в начале координат под углом a к горизонту с начальной скоростью u0. Траектория полета тела лежит в плоскости x, y (см. рис. 1.7, ось z направлена на нас). Пренебрегая сопротивлением воздуха, найти зависимость от времени: а) момента M силы, действующего на частицу; б) момента импульса частицы L. Оба момента рассчитывать относительно начала координат.
Ответ: 
,
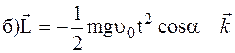
где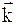 
– единичный вектор оси z.
4. В системе, показанной на рис. 1.8, известны масса m груза А, масса М ступенчатого шкива В, момент инерции I последнего относительно его оси и радиусы ступеней шкива R и 2R. Масса нитей пренебрежимо мала. Найти ускорение a груза А.
Ответ: 
.
 |
5. Сплошной однородный цилиндр А массой m1 может свободно вращаться вокруг горизонтальной оси, которая укреплена на подставке В массой m2. На цилиндр плотно намотана легкая нить, к концу К которой приложили постоянную горизонтальную силу F (см. рис. 1.9). Трения между подставкой и опорной горизонтальной плоскостью нет. Найти: а) ускорение точки К; б) кинетическую энергию T этой системы через t секунд после начала движения.
Ответ: 
 |
6. Два одинаковых груза массой m подвешены в одной точке к вертикальной оси на нитях длиной l. Определить их кинетическую энергию T, если при вращении они отклонились на угол a.
Ответ: Ek=mglsin atg a.
7. Шар и цилиндр, двигаясь с одинаковой начальной скоростью вкатываются без проскальзывания вверх по наклонной плоскости. Найти отношение высот подъема. Какое из тел поднимется выше?
Ответ: 
.
8. С какой скоростью должен въехать велосипедист в нижнюю точку мертвой петли радиусом R=10 м, чтобы не сорваться вниз в верхней ее точке? Масса велосипедиста с велосипедом M=90 кг, масса обоих колес m=6 кг. Трением пренебречь, момент инерции колеса рассчитывать как момент инерции обода.
Ответ: u=21,2 м/с.
9. Однородный шар массой m=5 кг скатывается без проскальзывания по наклонной плоскости, составляющий угол a=30 0 с горизонтом. Найти кинетическую энергию T шара через t=1,6 секунд после начала движения.
 |
Ответ: 
кДж.
10. Однородный цилиндр массой m=8 кг и радиусом R=1,3 см в момент t=0 начинает опускаться под действием силы тяжести (cм. рис 1.10). Пренебрегая массой нити, найти: а) угловое ускорение цилиндра e; б) зависимость от времени мгновенной мощности N, которую развивает сила тяжести.
Ответ: а)e=2g(3R)=5×10 2 рад/с 2 ; б) N=2mg 2 (t/3).
2. СТО, молекулярная физика и термодинамика
📹 Видео
Момент инерцииСкачать
Урок 111. Задачи на закон сохранения момента импульса (ч.1)Скачать
Якута А. А. - Механика - Теорема Эйлера. Момент инерции. Тензор инерцииСкачать
Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать
Расчет момента инерции цилиндраСкачать
Расчет момента инерции диска или цельного цилиндраСкачать
Куб и цилиндр: задача по стереометрииСкачать
Механика Л8. 2022. Уравнение Мещерского. Формула Циолковского. Проблема Лапласовского детерминизмаСкачать
Якута А. А. - Механика - Свойства осевого момента инерции. Центр удара. ГироскопыСкачать
КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать
Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать
РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать
Консультация к письменному Гос. экзамену по общей физике, Лёша Свинцицкий, 14.01.24Скачать
ЕГЭ физика .2 задание #8933Скачать
Задача на теорему об изменении кинетической энергииСкачать
11 класс, 32 урок, Объем цилиндраСкачать
Кинематические связи в задачах динамики | Олимпиадная физика, динамика | 10, 11 класс LIVEСкачать
Уравнение Мещерского и формула Циолковского LIVE | 11 класс, студенты МФТИ | Вузовская физика с FСкачать
