Рассмотрим однородные показательные уравнения второй и третьей степени (1-й — здесь).
Однородное уравнение — это уравнение, все члены которого имеют одинаковую суммарную степень.
Однородные уравнения второй степени в общем виде можно записать так:
где k1, k2, k3, a и b — некоторые числа, причём a и b — положительны и отличны от единицы.
Чтобы прийти к такому виду, почти всегда уравнение требуется предварительно преобразовать. Чаще всего уравнение записывают в виде
Запишем признаки, которые позволят отличить однородное уравнение от уравнений другого вида.
Признаки однородного показательного уравнения второй степени
- уравнение содержит ровно три степени с разными основаниями;
- показатели двух степеней ровно в два раза больше показателя третьей степени;
- основание этой третьей степени равно произведению оснований двух других степеней.
Однородные показательные уравнения второй степени решаются почленным делением обеих частей на наибольшую из степеней.
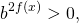
деление на степень не приводит к потере корней (то есть получаем уравнение, равносильное предыдущему).
ОДЗ: x∈R.Перепишем уравнение в виде
Разделим обе расти уравнения почтенно на 3 в степени 2x:
После упрощения приходим к уравнению
Это уравнение сводится к квадратному при помощи замены
где t>o. Оба корня квадратного уравнения
удовлетворяют условию t>0. Обратная замена
Сначала избавляемся от числовых слагаемых в показателях степеней, используя свойства степеней
представим степень с основанием 15 в виде произведения степеней с основаниями 3 и 5:
Делим обе части уравнения на 5 в степени 2x:
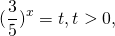
Оба корня положительны. Возвращаемся к исходной переменной:
По такому же принципу решаются однородные показательные уравнения 3-й степени.
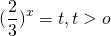
приводит к уравнению третьей степени
Представим -2=-1-1 и сгруппируем слагаемые
Общий множитель (t-1) вынесем за скобки
Получили уравнение типа «произведение равно нулю». приравниваем к нулю каждый множитель
Корень 1-го уравнения — t=1, второе уравнение не имеет корней. Обратная замена
- Как решать показательные уравнения?
- Простейшие показательные уравнения
- Общий метод решения показательных уравнений
- Решение показательных уравнений при помощи замены
- Показательные уравнения и неравенства с примерами решения
- Решении показательных уравнений
- Показательные уравнения и их системы
- Пример №1
- Пример №2
- Пример №3
- Пример №4
- Пример №5
- Пример №6
- Системы простейших показательных уравнений
- Пример №7
- Пример №8
- Пример №9
- Приближенное решение уравнений
- Пример №10
- Нахождение приближенного корня с заданной точностью
- Пример №11
- 📹 Видео
Видео:Показательные уравнения. Часть 3 из 3. Однородные уравненияСкачать

Как решать
показательные уравнения?
Решение уравнений – навык, который необходим каждому нацеленному на успешную сдачу ЕГЭ и ОГЭ школьнику. Это поможет решить задания №5, 13 и 15 из профильного уровня математики.
Одна из их разновидностей – степенные уравнения, которые иногда также называют показательными. Основная отличительная особенность – наличие переменной (х) не в основании степени, а в самом показателе. Как это выглядит:
Не бойтесь – это самый общий вид показательных уравнений. Реальные примеры выглядят как-то так:
Внимательно посмотрите на приведенные уравнения. В каждом из них присутствует, так называемая, показательная (степенная) функция. При решении необходимо помнить об основных свойствах степени, а также использовать особые правила, помогающие вычислить значение (х). Познакомиться с понятием степени и ее свойствами можно тут и тут.
И вам понадобится умение решать обыкновенные линейные и квадратные уравнения, те, что вы проходили в 7-8 классе. Вот такие:
И так, любое уравнение, в котором вы увидите показательную (степенную) функцию, называется показательным уравнением. Кроме самой показательной функции в уравнении могут быть любые другие математические конструкции – тригонометрические функции, логарифмы, корни, дроби и т.д. Если вы видите степень, значит перед вам показательное уравнение.
Ура! Теперь знаем, как выглядят показательные уравнения, но толку от этого не очень много. Было бы неплохо научиться их решать. Отличная новость – на наш взгляд показательные уравнения одни из самых простых типов уравнений, по сравнению с логарифмическими, тригонометрическими или иррациональными.
Видео:Показательные уравнения. 11 класс.Скачать

Простейшие показательные уравнения
Давайте начнем с самых простых типов уравнений и разберем сразу несколько примеров:
Что такое решить уравнение? Это значит, что нужно найти такое число, которое при подстановке в исходное уравнение вместо (х) даст верное равенство. В нашем примере нужно найти такое число, в которое нужно возвести двойку, чтобы получить восемь. Ну это просто:
Значит, если (х=3), то мы получим верное равенство, а значит мы решили уравнение.
Решим что-нибудь посложнее.
Такое уравнение выглядит сложнее. Попробуем преобразовать правую часть уравнения:
Мы применили свойство отрицательной степени по формуле:
Теперь наше уравнение будет выглядеть так:
Заметим, что слева и справа у нас стоят показательные функции, и там, и там основания одинаковые и равны (3), только вот степени разные – слева степень ((4х-1)), а справа ((-2)). Логично предположить, что если степени у такой конструкции будут равны, при условии, что основания одинаковые, то мы получим верное равенство. Так и поступим:
Такое мы решать умеем, ведь это обыкновенное линейное уравнение.
Поздравляю, мы нашли корень нашего показательного уравнения.
Попробуем поступить так, как в предыдущем примере – преобразуем левую и правую часть, чтобы слева и справа была показательная функция с одинаковым основанием. Как это сделать? Обращаем внимание, что (125=5*5*5=5^3), а (25=5*5=5^2), подставим:
Воспользуемся одним из свойств степеней ((a^n)^m=a^):
И опять мы получили две показательные функции, у которых одинаковые основания и для того, чтобы равенство выполнялось, необходимо приравнять из степени:
И еще один пример:
Те, кто хорошо знает свойства степеней, знают, что показательная функция не может быть отрицательной. Действительно, попробуйте возводить (2) в различную степень, вы никогда не сможете получить отрицательное число.
Внимание! Показательная функция не может быть отрицательной, поэтому, когда вы встречаете примеры на подобии примера 4, то знайте, что такого быть не может. Здесь корней нет, потому что показательная функция всегда положительна.
Теперь давайте разработаем общий метод решения показательных уравнений. И научимся решать более сложные примеры.
Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Общий метод решения показательных уравнений
Пусть у нас есть вот такой пример:
Где (a,b) какие-то положительные числа. ((a>0, ; b>0).
Согласно разобранным выше примерам, логично предположить, что для того, чтобы решить данное уравнение, нужно его преобразовать к виду, где слева и справа стоят показательные функции с одинаковым основанием. Так и поступим.
Слева у нас уже стоит (a^x), с этим ничего делать не будем, а вот справа у нас стоит загадочное число (b), которое нужно попытаться представить в виде (b=a^m). Тогда уравнение принимает вид:
Раз основания одинаковые, то мы можем просто приравнять степени:
Вот и весь алгоритм решения. Просто нужно преобразовать исходное уравнение таким образом, чтобы слева и справа стояли показательные функции с одинаковыми основаниями, тогда приравниваем степени и вуаля – сложное показательное уравнение решено. Осталось только разобраться, как так преобразовывать. Опять разберем на примерах:
Замечаем, что (16=2*2*2*2=2^4) это степень двойки:
Основания одинаковые, значит можно приравнять степени:
$$x=4.$$
Пример 6 $$5^=125 Rightarrow 5^=5*5*5 Rightarrow 5^=5^3 Rightarrow –x=3 Rightarrow x=-3.$$
Пример 7 $$9^=81 Rightarrow (3*3)^=3*3*3*3 Rightarrow(3^2)^=3^4 Rightarrow 3^=3^4 Rightarrow 8x=4 Rightarrow x=frac.$$
Здесь мы заметили, что (9=3^2) и (81=3^4) являются степенями (3).
Все здорово, но проблема в том, что такая схема решения показательных уравнений работает не всегда. Что делать, если привести к одинаковому основанию не получается. Например:
(3) и (2) привести к одинаковому основанию затруднительно. Но тем не менее мы должны это сделать. Воспользуемся следующей схемой преобразований: пусть есть некоторое положительное число (b>0), тогда его можно представить в виде степени любого, нужного вам, положительного числа не равного единице (a>0, ; a neq 1):
Эта очень важная формула, рекомендуем ее выучить. Вернемся к нашему примеру и по формуле представим (2) в виде (3) в какой-то степени, где (a=3), а (b=2):
Подставим данное преобразование в наш пример:
Получили равенство двух показательных функций с одинаковым основанием, значит можем приравнять их степени:
Так в ответ и запишем. Никакой ошибки здесь нет, дело в том, что такие логарифмы можно посчитать только на калькуляторе, поэтому на ЕГЭ или в контрольной работе вы просто оставляете ответ в таком виде.
Кто забыл, что такое логарифм, можно посмотреть здесь.
Рассмотрим еще несколько аналогичных примеров.
Те, кто хорошо знает свойства логарифмов, могут поиграться с последней формулой и получить ответ в разном виде:
Все эти варианты ответа верные, их можно смело писать в ответ.
И так, мы с вами научились решать любые показательные уравнения вот такого вида: (a^x=b), где (a>0; ; b>0).
Но это еще далеко не все. Часто вы будете встречать показательные уравнения гораздо более сложного типа. В ЕГЭ по профильной математике это номер 15 из 2й части. Но бояться тут не нужно, все на первый взгляд сложные уравнения при помощи обычно не самых сложных преобразований сводятся к уравнениям типа (a^x=b), где (a>0; ; b>0). Рассмотрим типы сложных уравнений, которые могут попасться:
Видео:Как решать Показательные Уравнения? (часть 2)Скачать

Решение показательных уравнений при помощи замены
Самое первое, что вы должны всегда делать, это пытаться привести все имеющиеся показательные функции к одинаковому основанию.
Здесь это сделать легко, замечаем, что (9=3^2), тогда (9^x=(3^2)^x=3^=(3^x)^2). Здесь мы воспользовались свойством степеней: ((a^n)^m=a^). Подставим:
Обратим внимание, что во всем уравнении все (х) «входят» в одинаковую функцию — (3^x). Сделаем замену (t=3^x, ; t>0), так как показательная функция всегда положительна.
Квадратное уравнение, которое решается через дискриминант:
Оба корня больше нуля, значит оба нам подходят. Сделаем обратную замену и уравнение сводится к решению двух простых показательных уравнений:
И второй корень:
И еще один пример на замену:
Воспользуемся нашим правилом, что все нужно приводить к одинаковому основанию – а стоп, тут и так у всех показательных функций основание (3). Давайте еще внимательно посмотрим на наш пример, очень похоже на то, что он тоже делается через замену. Но у нас тут нет одинаковых показательных функций, основания то одинаковые, а вот степени отличаются. Но если быть внимательным, то можно заметить, что в первой степени можно разбить свободный член (3=2+1) и вынести общий множитель (2):
Подставим в исходное уравнение:
Теперь показательные функции одинаковы и можно сделать замену:
Обратная замена, и наше уравнение сводится к простейшему:
И второе значение (t):
Тут у нас две показательные функции с основаниями (7) и (3), и как сделать из них одинаковые основания непонятно. Этот пример решается при помощи деления. Давайте поделим все наша уравнение на (3^x):
Здесь нам придется воспользоваться свойствами степеней:
Разберем каждое слагаемое:
Теперь подставим получившееся преобразования в исходное уравнение:
Теперь видно, что в нашем уравнении есть одинаковая функция, которую можно убрать в замену (t=(frac)^x):
Сделаем обратную замену:
И последний пример на замену:
Первым делом нужно сделать так, чтобы все показательные функции были с одинаковым основанием и в идеале с одинаковой степенью. Для этого нам понадобятся формулы для степеней:
Разберем каждое слагаемое нашего уравнения:
Все десятичные дроби всегда разумно представить в виде обыкновенных дробей. И будьте внимательны — отрицательная степень не имеет никакого отношения к знаку показательной функции!
И последнее слагаемое со степенью:
Подставим все наши преобразования в исходное уравнение:
Теперь можно сделать замену (t=2^x) или можно обойтись без замены, просто приведя подобные слагаемые (вынести общий множитель (2^x)):
Особенно стоит подчеркнуть прием, который мы использовали при решении 13-го примера. Всегда старайтесь избавляться от десятичных дробей. Переводите их в обыкновенные дроби.
И другой тип степенных уравнений, где обычно не нужно делать замену, а необходимо отлично знать все свойства степеней, некоторые из них мы уже обсудили выше. Все про свойства степеней можно посмотреть тут
Вот такое уравнение, в котором у нас, во-первых, показательных функции перемножаются, а еще хуже то, что у них у всех разные основания. Катастрофа, а не пример. Но ничего, все не так страшно, как кажется. Внимательно посмотрите на основания: у нас есть в основании (2), (5) и (10). Очевидно, что (10=2*5). Воспользуемся этим и подставим в наше уравнение:
Воспользуемся формулой ((a*b)^n=a^n*b^n):
И перекинем все показательные функции с основанием (2) влево, а с основанием (5) вправо:
Сокращаем и воспользуемся формулами (a^n*a^m=a^) и (frac=a^):
Самая главная идея при решении показательных уравнений – это любыми доступными способами свести все имеющиеся степенные функции к одинаковому основанию. А еще лучше и к одинаковой степени. Вот почему необходимо знать все свойства степеней, без этого решить уравнения будет проблематично.
Как же понять, где какие преобразования использовать? Не бойтесь, это придет с опытом, чем больше примеров решите, тем увереннее будете себя чувствовать на контрольных в школе или на ЕГЭ по профильной математике. Сначала потренируйтесь на простых примерах и постепенно повышайте уровень сложности. Успехов в изучении математики!
Видео:9.5. Показательные уравнения. Однородные уравнения.Скачать

Показательные уравнения и неравенства с примерами решения
Содержание:
Рассмотрим уравнения, в которых переменная (неизвестное) находится в показателе степени. Например:
Уравнения такого вида принято называть показательными.
Видео:Урок 4. Однородные показательные уравнения. Алгебра 10, 11 классСкачать

Решении показательных уравнений
При решении показательных уравнений нам будет полезно следствие из теоремы о свойствах показательной функции.
Пусть
Каждому значению показательной функции 
Пример:
Решение:
Согласно следствию из равенства двух степеней с одинаковым основанием 3 следует равенство их показателей. Таким образом, данное уравнение равносильно уравнению
Пример:
Решение:
а) Данное уравнение равносильно (поясните почему) уравнению
Если степени с основанием 3 равны, то равны и их показатели:
Решив это уравнение, получим
Ответ:
При решении каждого уравнения из примера 2 сначала обе части уравнения представили в виде степени с одним и тем же основанием, а затем записали равенство показателей этих степеней.
Пример:
Решение:
а) Данное уравнение равносильно уравнению
Решая его, получаем:
Так как две степени с одинаковым основанием 2 равны, то равны и их показатели, т. е. 
б) Разделив обе части уравнения на 

Ответ:
При решении примера 3 а) левую часть уравнения разложили на множители. Причем за скобку вынесли такой множитель, что в скобках осталось числовое выражение, не содержащее переменной.
Пример:
Решить уравнение
Решение:
Обозначим 
Таким образом, из данного уравнения получаем
откуда находим:
Итак, с учетом обозначения имеем:
При решении примера 4 был использован метод введения новой переменной, который позволил свести данное уравнение к квадратному относительно этой переменной.
Пример:
Решить уравнение
Решение:
Можно заметить, что 2 — корень данного уравнения. Других корней уравнение не имеет, так как функция, стоящая в левой части уравнения, возрастающая, а функция, стоящая в правой части уравнения, убывающая. Поэтому уравнение имеет не более одного корня (см. теорему из п. 1.14).
Пример:
Решить уравнение
Решение:
Пример:
При каком значении а корнем уравнения 
Решение:
Поскольку х = 2 — корень, то верно равенство
Решив это уравнение, найдем
Ответ: при
Показательные уравнения и их системы
Показательным уравнением называется уравнение, в ко тором неизвестное входит в показатель степени. При решении показательных уравнений полезно использовать следующие тождества:
Приведем методы решения некоторых типов показательных уравнений.
1 Приведение к одному основанию.
Метод основан на следующем свойстве степеней: если две степени равны и равны их основания, то равны и их показатели, т.е. уравнения надо попытаться привести к виду 
Пример №1
Решите уравнение
Решение:
Заметим, что 
Применив тождество (1), получим Зх — 7 = -7х + 3, х = 1.
Пример №2
Решить уравнение
Решение:
Переходя к основанию степени 2, получим:
Согласно тождеству (2), имеем
Последнее уравнение равносильно уравнению 4х-19 = 2,5х.
2 Введение новой переменной.
Пример №3
Решить уравнение
Решение:
Применив тождество 2, перепишем уравнение как
Введем новую переменную: 
которое имеет корни 


Пример №4
Решить уравнение
Решение:
Разделив обе части уравнения на 
последнее уравнение запишется так:
Решая уравнение, найдем
Значение 

Пример №5
Решить уравнение
Решение:
Заметим что 
Перепишем уравнение в виде
Обозначим 
Получим
Корнями данного уравнения будут
Следовательно,
III Вынесение общего множителя за скобку.
Пример №6
Решить уравнение
Решение:
После вынесения за скобку в левой части 



Системы простейших показательных уравнений
Пример №7
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей
системе :
Очевидно, что последняя система имеет решение
Пример №8
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей системе: 
Умножив второе уравнение этой системы на (-2) и сложив с первым, получим уравнение —9х=-4. Отсюда, найдем 
Пример №9
Решите систему уравнений:
Решение:
Сделаем замену: 
Очевидно, что эта система уравнений имеет решение
Тогда получим уравнения
Приближенное решение уравнений
Пусть многочлен f(х) на концах отрезка [a,b] принимает значения разных знаков, то есть 

Это утверждение проиллюстрировано на следующем чертеже.
Рассмотрим отрезок 
Метод последовательного деления отрезка пополам заключается в последовательном разделении отрезка [a, b] пополам до тех пор, пока длина полученного отрезка не будет меньше заданной точности
- вычисляется значение f(х) выражения
- отрезок делится пополам, то есть вычисляется значение
- вычисляется значение
выражения f(х) в точке
- проверяется условие
- если это условие выполняется, то в качестве левого конца нового отрезка выбирается середина предыдущего отрезка, то есть полагается, что
(левый конец отрезка переходит в середину);
- если это условие не выполняется, то правый конец нового отрезка переходит в середину, то есть полагается, что b=x;
- для нового отрезка проверяется условие
- если это условие выполняется , то вычисления заканчиваются. При этом в качестве приближенного решения выбирается последнее вычисленное значение х. Если это условие не выполняется, то, переходя к пункту 2 этого алгоритма, вычисления продолжаются.
Метод последовательного деления пополам проиллюстрирован на этом чертеже:
Для нахождения интервала, содержащего корень уравнения 
Оказывается, что для корня 


Пример №10
Найдите интервал, содержащий корень уравнения
Решение:
Поделив обе части уравнения на 2 , получим,
Так как, для нового уравнения
Значит, в интервале, 




Значит, уравнение имеет корень, принадлежащий интервалу (-1; 0).
Нахождение приближенного корня с заданной точностью
Исходя из вышесказанного, заключаем, что если выполнено неравенство 



корень уравнения с точностью 




Пример №11
Найдите приближенное значение корня уравнения 
Решение:
Из предыдущего примера нам известно, что корень лежит в интервале
(-1; 0). Из того, что 
Так как, |(-0,25)41,5(-0,25)2+2,5(-0,25)+0,5| = |-0,046| 1. Если
Пусть
Изображения графиков показательной функции подсказывают это свойство. На рисунке 27 видно, что при а > 1 большему значению функции соответствует большее значение аргумента. А на рисунке 30 видно, что при 0
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📹 Видео
11 класс, 12 урок, Показательные уравненияСкачать

Однородные показательные уравненияСкачать

Однородные показательные уравненияСкачать

ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 10 класс решение показательных уравненийСкачать

№10 Показательные уравнения. Однородные. Подготовка к ЕГЭ по математике.Скачать

№9 Показательные уравнения. Однородные. Подготовка к ЕГЭ по математике.Скачать

Сложные показательные уравнения: примеры и способы решенияСкачать

Показательные уравнения с ЕГЭ: логарифмирование и однородное.Скачать

ЕГЭ 2017. Решение показательных уравнений. Однородное показательное уравнениеСкачать

Это просто! Как решать Показательные Неравенства?Скачать

ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ😩 #математика #shorts #егэ #огэ #уравнение #показательныеуравненияСкачать

Показательные уравнения. ОднородныеСкачать

Простейшие и однородные показательные уравненияСкачать

N13 Профилный ЕГЭ. Однородное показательное уравнение второго порядка. Алгоритм решения и пример.Скачать

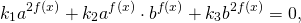
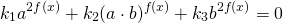
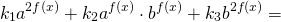
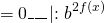
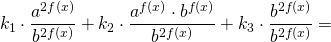
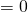
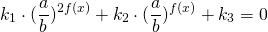
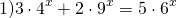
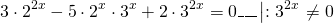
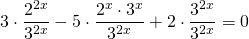
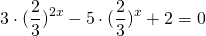
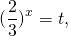
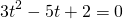
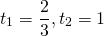
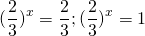
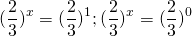
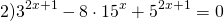
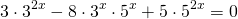
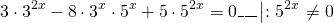
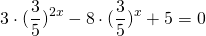
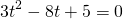
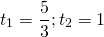
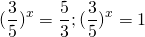
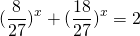
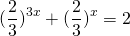
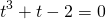
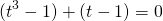
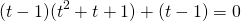
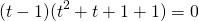
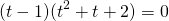
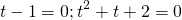










































































 выражения f(х) в точке
выражения f(х) в точке 

 (левый конец отрезка переходит в середину);
(левый конец отрезка переходит в середину);










