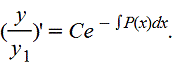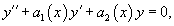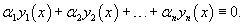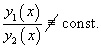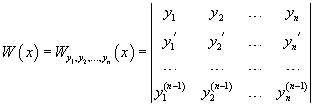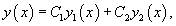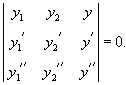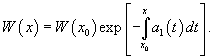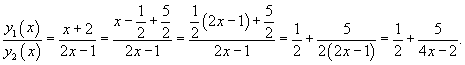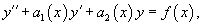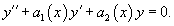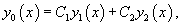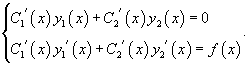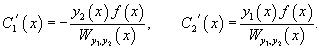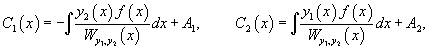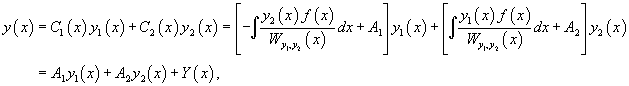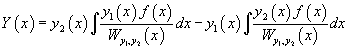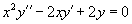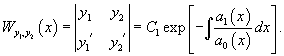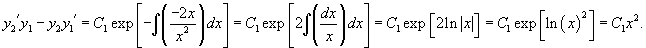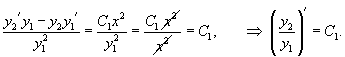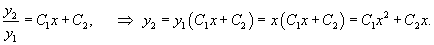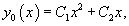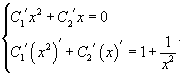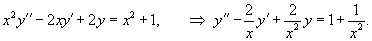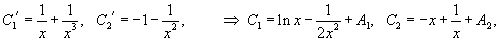Однородные дифференциальные уравнения с переменными коэффициентами

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

Линейные однородные дифференциальные уравнения 2-го порядка с переменными коэффициентами.

a_o(x)y»+a₁(x)y’+a₂(x)y=0, где (a_o(x), a₁(x), a₂(x)) — непрерывные функции на некотором интервале (a,b).

Предположим, что известночастное решение y₁(x)этого уравнения. Чтобы получить общее решение y(x), рекомендуется воспользоваться формулой Острогадского — Лиувилля

,

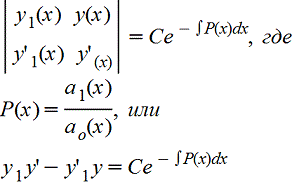
а это уже уравнение 1го порядка относительно y(x). Далее, деля левую и правую части на y₁ 2 (x) , имеем

После интегрирования получим общее решение исходного уравнения.

Замечание 1.

Общего способа отыскания частного решения y₁(x) линейного уравнения не существует. Иногда удается найти его путем подбора или в виде алгебраического многочлена y₁(x)=x n +a₁x n-1 +. +a_n или в виде показательной функцииy₁(x)=e ax или и т.д.

Замечание 2.

Если известно y₁(x), то порядок уравнения можно понизить, сохраняя линейность и следующим способом. В исходное уравнение надо подставить y₁(x)z(x) и затем сделать замену z'(x)=u(x). Но лучше все же пользоваться формулой Острогадского — Лиувилля.

Видео:Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

ЛДУ с переменными коэффициентами. Метод Лагранжа

Видео:15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Линейные дифференциальные уравнения с переменные коэффициентами

Если известно частное решение уравнения

то его порядок можно понизить на единицу (не нарушая линейности уравнения), полагая , где — новая неизвестная функция, а затем делая замену (можно непосредственно делать замену ).

Если известно частных линейно независимых решений уравнения (32), то порядок уравнения может быть понижен на единиц.

Общее решение уравнения

есть сумма какого-нибудь его частного решения и общего решения соответствующего однородного уравнения (32).

Если известна фундаментальная система соответствующего однородного уравнения (32), то общее решение неоднородного уравнения (33) может быть найдено методом вариации постоянных ( метод Лагранжа ).

Общее решение уравнения (32) имеет вид

где — произвольные постоянные.

Будем искать решение уравнения (33) в виде

где — некоторые пока неизвестные функции от . Для их определения получаем систему

Разрешая эту систему относительно , получаем

где — произвольные постоянные. Внося найденные значения в (34), получаем общее решения уравнения (33).

В частности, для уравнения второго порядка

Решая (36) относительно и , получаем

где и — постоянные интегрирования.

Замечание. Для уравнения , где , система (36) будет выглядеть так:

Пример 1. Найти общее решение уравнения , если есть его частное решение.

Решение. Положим , где — новая неизвестная функция от , тогда

Подставляя в данное уравнение, получаем

Но так как есть частное решение данного уравнения, то , поэтому имеем

Но , а значит , и уравнение (37) примет вид

Перепишем его в виде . Отсюда имеем , откуда

Интегрируя это уравнение, найдем и, следовательно, общее решение данного уравнения будет

Пример 2. Найти общее решение уравнения .

Решение. Общее решение соответствующего однородного уравнения имеет вид (см. пример 1)

и следовательно, его фундаментальная система решений будет

Будем искать общее решение данного уравнения методом вариации произвольных постоянных:

где — постоянные неизвестные функции от , подлежащие определению. Для их нахождения составим следующую систему:

Отсюда находим: . Интегрируя, получаем

Подставляя эти значения и в выражение для , найдем общее решение данного уравнения

Пример 3. Решить уравнение .

Решение. Соответствующее однородное уравнение будет . Его характеристическое уравнение имеет мнимые корни , и общее решение однородного уравнения имеет вид

Общее решение исходного уравнения ищем в виде

где и — неизвестные функции от . Для их нахождения составим систему

Разрешаем эту систему относительно и :

Подставляя выражения и в (38), получаем общее решение данного уравнения

Здесь есть частное решение исходного неоднородного уравнения.

Пример 4. Зная фундаментальную систему решений соответствующего однородного уравнения, найти частное решение уравнения

Решение. Применяя метод вариации постоянных, находим общее решение уравнения (39):

При первые два слагаемых правой части (40) стремятся к бесконечности, причем при любых , неравных нулю одновременно, функция есть бесконечно большая функция при . Третье слагаемое правой части (40) имеет пределом ноль при , что легко установить с помощью правила Лопиталя. Таким образом, функция , которая получается из (40) при и , будет решением уравнения (39), удовлетворяющим условию .

Видео:Однородное линейное дифференциальное уравнение. Алгоритм решенияСкачать

Составление дифференциального уравнения по заданной фундаментальной системе решений

Рассмотрим линейно независимую на отрезке систему функций

имеющих все производные до n-го порядка включительно. Тогда уравнение

где — неизвестная функция, будет линейным дифференциальным уравнением, для которого, как нетрудно видеть, функции составляют фундаментальную систему решений. Коэффициент при в (42) есть определитель Вронского системы (41). Те точки, в которых этот определитель обращается в ноль, будут особыми точками построенного уравнения — в этих точках обращается в ноль коэффициент при старшей производной .

Пример 1. Составить дифференциальное уравнение, для которого образуют фундаментальную систему решений.

Решение. Применяя формулу (42), получаем

Раскрывая определитель в левой части (43) по элементам третьего столбца, будем иметь . Это и есть искомое дифференциальное уравнение.

Пример 2. Составить дифференциальное уравнение, для которого функции фундаментальную систему решений образуют функции .

Решение. Составим уравнение вида (42):

Раскрывая последний определитель по элементам 3-го столбца, будем иметь

В этом примере определитель Вронского обращается в ноль при . Это не противоречит общей теории, в силу которой определитель Вронского фундаментальной системы решений линейного однородного дифференциального уравнения

с непрерывными на отрезке коэффициентами не обращается в ноль ни в одной точке отрезка . Записав уравнение (44) в виде

видим, что коэффициент при терпит разрыв при , так что в точке непрерывность коэффициентов уравнения (45) нарушается.

Видео:4. Однородные дифференциальные уравнения (часть 1)Скачать

Разные задачи

Пусть — фундаментальная система линейного однородного уравнения

Тогда имеет место формула Остроградского–Лиувилля

где — определитель Вронского, а — любое значение из отрезка , на котором непрерывны коэффициенты уравнения.

Пример 1. Показать, что линейное дифференциальное уравнение имеет решение вида , где — некоторый многочлен. Показать, что второе решение этого уравнения имеет вид , где — также многочлен.

Решение. Будем искать решение в виде многочлена, например, первой степени: . Подставляя в уравнение, найдем, что . Пусть , тогда ;. таким образом, многочлен будет решением данного уравнения. Перепишем данное уравнение в виде

Пусть — второе частное решение данного уравнения, линейно независимое с первым. Находим определитель Вронского системы решений

здесь . Применяя формулу Остроградского–Лиувилля, будем иметь

где — любое значение , причем , или ; здесь . Для нахождения получили линейное дифференциальное уравнение первого порядка. Деля обе части этого уравнения на , приведем его к виду

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Однородные дифференциальные уравнения с переменными коэффициентами

Если же это тождество выполняется лишь при , то указанные функции , , . называются линейно независимыми на отрезке .

Для случая двух функций критерий линейной независимости можно записать в более простом виде: Функции , будут линейно независимыми на отрезке , если их отношение на данном отрезке тождественно не равно постоянной:

В противном случае, при 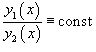, эти функции будут линейно зависимыми .

Пусть n функций , , . имеют производные порядка. Определитель

называется определителем Вронского или вронскианом для указанной системы функций.

Теорема . Если система функций , , . линейна зависима на отрезке , то ее определитель Вронского тождественно равен нулю на этом отрезке.

Отсюда следует, что если определитель отличен от нуля хотя бы в одной точке отрезка , то функции , , . будут линейно независимыми. Это свойство определителя Вронского позволяет выяснить, являются ли найденные решения однородного дифференциального уравнения линейно независимыми.

Совокупность двух линейно независимых частных решений линейного однородного дифференциального уравнения второго порядка образует его фундаментальную систему решений .

Если , − фундаментальная система решений, то общее решение уравнения второго порядка представляется в виде

где , − произвольные постоянные.

Заметим, что по заданной фундаментальной системе решений , можно построить соответствующее однородное дифференциальное уравнение. Для случая второго порядка такое уравнение выражается через определитель в виде:

Итак, как указано выше, общее решение однородного дифференциального уравнения второго порядка является линейной комбинацией двух линейно независимых частных решений , этого уравнения.

Очевидно, что частные решения зависят от коэффициентов дифференциального уравнения. Формула Лиувилля-Остроградского устанавливает связь между вронскианом , построенном на базе частных решений , , и коэффициентом в дифференциальном уравнении.

Пусть − определитель Вронского решений , линейного однородного дифференциального уравнения 2-го порядка

К сожалению, общего метода отыскания частного решения не существует. Обычно это можно сделать путем подбора.

Если известно частное решение линейного однородного уравнения второго порядка, то его можно преобразовать к линейному уравнению первого порядка с помощью подстановки и последующей замены .

Другой способ понижения порядка основан на использовании формулы Лиувилля-Остроградского. Здесь также одно частное решение должно быть известно. Соответствующие примеры разобраны ниже.

где , и − непрерывные функции на отрезке .

Соответствующее однородное уравнение записывается в виде

Метод вариации постоянных (или метод Лагранжа) используется для построения общего решения неоднородного уравнения, когда известно общее решение ассоциированного с ним однородного уравнения.

Пусть общее решение однородного уравнения 2-го порядка выражается через фундаментальную систему решений и :

где C₁, C₂ − произвольные постоянные. Идея данного метода состоит в том, что вместо постоянных C₁ и C₂рассматриваются функции и , которые подбираются таким образом, чтобы решение удовлетворяло неоднородному уравнению.

Производные неизвестных функций и можно определить из системы уравнений

Применяя метод вариации параметров, важно помнить, что функция должна соответствовать дифференциальному уравнению, приведенному к стандартному виду, т.е. коэффициент перед старшей производной должен быть равен 1.

Далее, зная производные и , можно найти и сами функции и :

Тогда общее решение исходного неоднородного уравнения будет выражаться формулой

Теперь воспользуемся методом вариации постоянных и построим общее решение неоднородного уравнения. Будем рассматривать параметры C₁ и C₂ как функции от переменной x. Производные этих функций определяются из системы уравнений

В результате получаем общее решение неоднородного уравнения в виде

📸 Видео

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Однородное дифференциальное уравнениеСкачать

ЛОДУ с переменными коэффициентами. Примеры.Скачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Дифференциальные уравнения, 3 урок, Однородные уравненияСкачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать

Линейное дифференциальное уравнение Коши-ЭйлераСкачать

5. Однородные дифференциальные уравнения. Часть 2.Скачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Дифференциальные уравнения, 8 урок, Линейные дифференциальные уравнения с const коэф-ами 2 порядкаСкачать

2. Линейные уравнения с переменными коэффициентамиСкачать

Однородные дифференциальные уравнения первого порядка #calculus #differentialequation #maths #Скачать