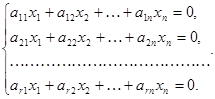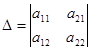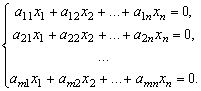Доказательство. Существование нетривиального решения системы (15) эквивалентно линейной зависимости столбцов матрицы системы (т.е. существуют такие числа х1, x2,…,xn, не все равные нулю, что справедливы равенства (15)).
По теореме о базисном миноре столбцы матрицы линейно зависимы Û, когда не все столбцы этой матрицы являются базисными, т.е. Û, когда порядок r базисного минора матрицы меньше числа n ее столбцов. Ч.т.д.
Следствие. Квадратная однородная система имеет нетривиальные решения Û, когда |А|=0.
Теорема 2. Если столбцы х (1) ,х (2) ,…,х ( s ) решения однородной системы АХ=0, то любая их линейная комбинация так же является решением этой системы.
Доказательство. Рассмотрим любую комбинацию решений:
х= 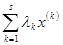
Тогда АХ=А( 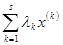
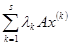
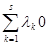
Следствие 1.Если однородная система имеет нетривиальное решение, то она имеет бесконечно много решений.
Т.о. необходимо найти такие решения х (1) ,х (2) ,…,х ( s ) системы Ах=0, чтобы любое другое решение этой системы представлялось в виде их линейной комбинации и притом единственным образом.
Определение. Система k=n-r (n –количество неизвестных в системе, r=rg A) линейно независимых решений х (1) ,х (2) ,…,х ( k ) системы Ах=0 называется фундаментальной системой решенийэтой системы.
Теорема 3. Пусть дана однородная система Ах=0 с n неизвестными и r=rg A. Тогда существует набор из k=n-r решений х (1) ,х (2) ,…,х ( k ) этой системы, образующих фундаментальную систему решений.
Доказательство. Не ограничивая общности, можно считать, что базисный минор матрицы А расположен в верхнем левом углу. Тогда, по теореме о базисном миноре, остальные строки матрицы А являются линейными комбинациями базисных строк. Это означает, что если значения х1,х2,…,xn удовлетворяют первым r уравнениям т.е. уравнениям, соответствующим строкам базисного минора), то они удовлетворяют и другим уравнениям. Следовательно, множество решений системы не изменится, если отбросить все уравнения начиная с (r+1)-го. Получим систему:
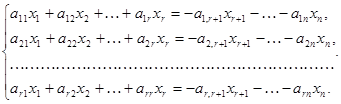
Т.к. в этом случае все bi=0, то вместо формул
cj= 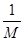
cj=- 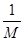
Если задать свободным неизвестным хr+1,хr+2,…,xn произвольные значения, то относительно базисных неизвестных получим квадратную СЛАУ с невырожденной матрицей, у которой существует единственное решение. Т.о., любое решение однородной СЛАУ однозначно определяется значениями свободных неизвестных хr+1,хr+2,…,xn. Рассмотрим следующие k=n-r серий значений свободных неизвестных:
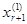
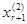
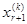
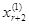
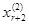
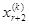
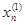
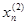
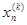
(Номер серии указан верхним индексом в скобках, а серии значений выписаны в виде столбцов. В каждой серии 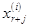
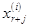
i-й серии значений свободных неизвестных однозначно соответствуют значения 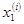
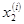
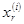
Покажем, что столбцы еi= 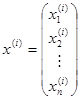
образуют фундаментальную систему решений.
Т.к. эти столбцы по построению являются решениями однородной системы Ах=0 и их количество равно k, то остается доказать линейную независимость решений (16). Пусть есть линейная комбинация решенийe1,e2,…,ek (х (1) , х (2) ,…,х ( k ) ), равная нулевому столбцу:
Тогда левая часть этого равенства является столбцом, компоненты которого с номерами r+1,r+2,…,n равны нулю. Но (r+1)-я компоненты равна l11+l20+…+lk0=l1. Аналогично, (r+2)-я компонента равна l2,…, k-я компонента равна lk. Поэтому l1=l2=…=lk=0, что и означает линейную независимость решений e1,e2,…,ek (х (1) , х (2) ,…,х ( k ) ).Ч.т.д.
Построенная фундаментальная система решений (18) называется нормальной. В силу формулы (13¢) она имеет следующий вид:
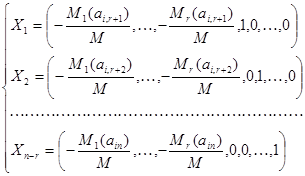
Следствие 2. Пусть e1,e2,…,ek-нормальная фундаментальная система решений однородной системы, тогда множество всех решений можно описать формулой:
где с1,с2,…,сk – принимают произвольные значения.
Доказательство. По теореме 2 столбец (19) является решением однородной системы Ах=0. Остается доказать, что любое решение 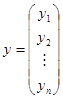
Доказанное утверждение справедливо не только для нормальной ФСР, но и для произвольной ФСР однородной СЛАУ.
Установим связь между решениями неоднородной СЛАУ 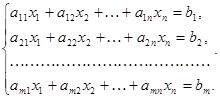
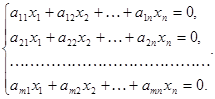
Теорема 4. Сумма любого решения неоднородной системы (1) и соответствующей ей однородной системы (15) является решением системы (1).
Доказательство. Если c1,…,cn – решение системы (1), а d1,…,dn — решение системы (15), то подставив в любое (например, в i-е) уравнение системы (1) на место неизвестных числа c1+d1,…,cn+dn, получим:
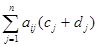
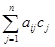

Теорема 5. Разность двух произвольных решений неоднородной системы (1) является решением однородной системы (15).
Доказательство. Если c¢1,…,c¢n и c²1,…,c²n – решения системы (1), то подставив в любое (например, в i-е) уравнение системы (1) на место неизвестных числа c¢1-с²1,…,c¢n-с²n, получим:
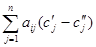
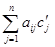
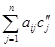
Из доказанных теорем следует, что общее решение системы m линейных однородных уравнений с n переменными равно сумме общего решения соответствующей ей системы однородных линейных уравнений (15) и произвольного числа частного решения этой системы (15).
В качестве частного решения неоднородной системы естественно взять то его решение, которое получается, если в формулах cj= 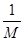
Х0=( 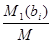
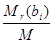
Рассмотрим систему двух уравнений с двумя переменными:
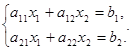
Для решения исключим х2, умножив первое уравнение на а22, а второе – на (-а12) и сложив их: 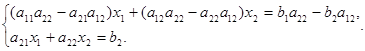
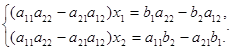
Обозначив 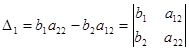
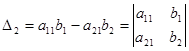
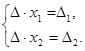
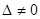
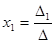
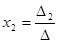
Если Δ=0, а 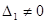
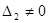
Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Однородная система линейных уравнений имеет нетривиальное решение тогда и только
Системы линейных однородных уравнений.
Фундаментальная система решений
Система линейных уравнений называется однородной, если все свободные члены уравнений равны нулю:
Однородная система всегда совместна, поскольку она всегда имеет тривиальное (нулевое) решение. Однако наибольший интерес представляют нетривиальные решения.
Теорема 1 . Однородная система линейных уравнений имеет нетривиальное решение тогда и только тогда, когда ранг матрицы системы меньше числа неизвестных: r ( A )= r n .
Справедливо следующее утверждение: линейная комбинация решений однородной системы линейных уравнений также является ее решением.
Максимальная линейно независимая система решений называется фундаментальной системой решений однородной системы уравнений. Фундаментальная система решений содержит ( n — r ) векторов. Любое решение системы может быть представлено в виде линейной комбинации векторов фундаментальной системы решений.
Для нахождения фундаментальной системы решений нужно:
1) r базисных переменных выразить через свободные переменные;
2) выбрать линейно независимую систему ( n — r ) векторов ( n — r )-мерного пространства (например, это могут быть единичные векторы);
3) поочередно заменить свободные переменные координатами векторов выбранной системы и вычислить значения базисных переменных.
Полученные решения 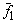
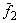
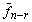
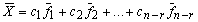
где 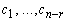
Видео:Видеоурок "Однородные системы линейных уравнений"Скачать

4.2.3 Системы линейных однородных уравнений
Рассмотрим систему вида

Где 

Однородная система линейных уравнений (1) всегда совместна, так как 
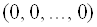
В каких случаях существует нетривиальное решение?
Теорема. Для того чтобы система (1) имела нетривиальные решения, необходимо и достаточно, чтобы ранг ее матрицы был меньше числа неизвестных.
Действительно, в этом случае есть свободные неизвестные, которым можно придавать любые, в том числе и ненулевые, значения.
Выделим частный случай систем (1), когда 
Теорема. Система (1) в случае 
Системы линейных однородных уравнений обладают важным свойством, которое сформулируем в виде теоремы.
Теорема. Любая линейная комбинация решений системы (1) также является решением этой системы.
Возникает вопрос, можно ли подобрать такую совокупность решений системы (1), чтобы любое решение системы можно было бы найти как линейную комбинацию этих решений? Такая совокупность решений существует и носит название фундаментальной.
Определение. Совокупность решений системы линейных однородных уравнений (1) называется фундаментальной системой решений, если эта совокупность состоит из линейно независимых решений и любое решение системы (1) является линейной комбинацией этих решений.
Теорема. Если ранг 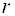

Пример 22. Найти общее решение и какую-нибудь фундаментальную систему решений для системы
 |
Решение. Алгоритм решения такой же, как и для систем линейных неоднородных уравнений.
Оперируя только со строками, находим ранг матрицы, базисный минор; объявляем зависимые и свободные неизвестные и находим общее решение.
Первая и вторая строки пропорциональны, одну из них вычеркнем:

Зависимые переменные – 





Общее решение имеет вид:
Находим фундаментальную систему решений, которая состоит из 

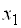



Таким образом, первое решение: 

Эти два решения составляют фундаментальную систему решений. Заметим, что фундаментальная система не единственна (определителей, отличных от нуля, можно составить сколько угодно).
Пример 22. Найти общее решение и фундаментальную систему решений системы

Отсюда следует, что ранг матрицы равен 3 и равен числу неизвестных. Значит, система не имеет свободных неизвестных, а поэтому имеет единственное решение – тривиальное.
Для самостоятельного решения.
1. Доказать, что система 
Найти ее общее и частное решения, приняв в качестве свободных неизвестных 

Ответ: 
2. Образуют ли строки каждой из матриц 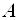



Ответ: строки матрицы 

3. Три прямые 


Ответ выбрать из списка: 1) система совместна, 


💥 Видео
Однородная система слау. Тривиальное решение. Ненулевое решениеСкачать

Фундаментальная система решений для однородной системы линейных уравненийСкачать

При каких λ однородная система уравнений имеет ненулевое решение?Скачать

§41 Решение систем линейных однородных уравненийСкачать

Неоднородная система линейных уравненийСкачать

ФСР. Система однородных уравнений. Общее решениеСкачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Математика без Ху!ни. Метод Гаусса.Скачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Решение системы линейных однородных уравнений (№726)Скачать

Общее, частное, базисное решение системы линейных уравнений Метод ГауссаСкачать

Система линейных однородных уравнений | Линейная алгебраСкачать

Решение системы уравнений методом ГауссаСкачать

Неоднородные системы линейных уравненийСкачать
Фундаментальная система решений системы линейных уравнений ФСР СЛАУСкачать

Совместные и несовместные, определенные и неопределенные системы линейных уравненийСкачать

ФСР. Система однородных уравнений 2Скачать

Решение однородных линейных систем. ТемаСкачать