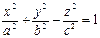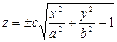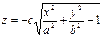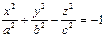Однополостный гиперболоид график и уравнение (2 видео)

6.6. Гиперболоиды

Их тоже два, и это тоже нечастые гости в массовой практике:

Содержание

Однополостной гиперболоид
Двуполостной гиперболоид
Постройте однополостный гиперболоид
Гиперболоиды: однополостный и двуполостный
Определение гиперболоида
Плоские сечения однополостного гиперболоида
Плоские сечения двуполостного гиперболоида
Гиперболоиды вращения
📽️ Видео

Однополостной гиперболоид

имеет каноническое уравнение , числа называют полуосями гиперболоида. Если его рассекать плоскостями , то будут получаться эллипсы: , которые неограниченно увеличиваются, когда мы уходим по оси вверх или вниз к бесконечности. Эллипс, лежащий в плоскости : называется горловым эллипсом, он самый маленький и хорошо просматривается на чертеже.

Если рассекать поверхность плоскостями, параллельными плоскостям , то в сечениях будут получаться гиперболы:

и эти гиперболы хорошо видны на поверхности. А посему и «гиперболоид».

Однополостной гиперболоид симметричен относительно всех координатных плоскостей, осей и начала координат.

Если , то мы имеем дело с гиперболоидом вращения: – он получен вращением гиперболы вокруг оси . Горизонтальные же сечения представляют собой окружности, в чём мы убедимся на конкретном примере:

Задача 182

Построить тело, ограниченное поверхностями

Решение: найдём пересечение гиперболоида с плоскостью : – горловая окружность радиуса 1. Найдём пересечение с плоскостью :
– окружность с центром в точке радиуса .

Изобразим на чертеже обе окружность и соединим их направляющими – 4 ветвями гиперболы.

Такой вот получился симпатичный горшок. …А вверху у меня чертёж, к слову, ассоциируется с унитазом 🙂

Двуполостной гиперболоид

имеет похожее каноническое уравнение . Поверхность представляет собой 2 бесконечные чаши с вершинами :

Для двуполостного гиперболоида справедливы почти все утверждения, что и для однополостного. Горизонтальные сечения плоскостями представляют собой эллипсы, а вертикальные – гиперболы. Но, естественно, тут нет горлового эллипса. Однако в плане симметрии всё так же.

Вообще, оба типа поверхностей можно назвать эллиптическими гиперболоидами, но это название не учитывает различие между ними. И поэтому их различают по количеству полостей – у предыдущего одна полость, а у этого – две.

И да, частный случай: – есть гиперболоид вращения.

Следующее задание для самостоятельного решения:

Задача 183

Построить тело, ограниченное поверхностями

С поверхностями всё! Теперь пару ласковых о координатах.

Как вы заметили, во всех случаях у нас фигурировала прямоугольная система координат, но в некоторых задачах бывают выгодны другие системы:

Видео:Поверхности второго порядкаСкачать

Постройте однополостный гиперболоид

Microsoft Excel

Задание 1. Постройте однополостный гиперболоид

1. Откройте файл под именем «Книга 1». На Листе 1 постройте поверхность, представляемую уравнением:

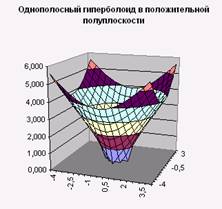
Такая поверхность называется однополосный гиперболоид.

2. Для построения этой поверхности решите заданное уравнение относительно z

3. Вам предстоит создать две таблицы для вычисления двух математических функций с двумя переменными

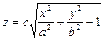
Первая функция представит однополосный гиперболоид в положительной полуплоскости, а вторая – в отрицательной.

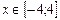
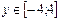
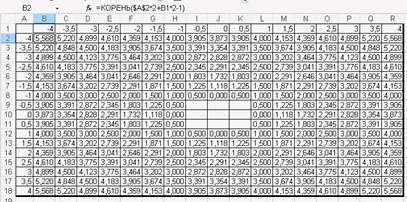
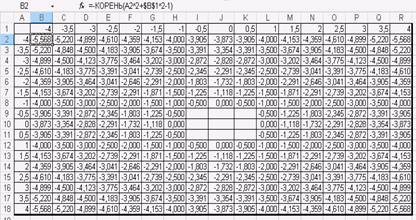
Пусть и . Для упрощения формул примите: a = b = c =1.

4. В таблице для вычисления первой функции (рис. 1) приведена формула, которую следует копировать по строкам и столбцам

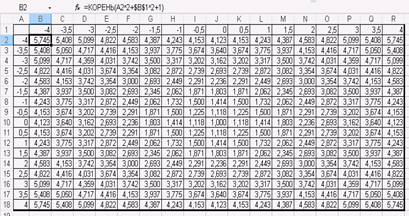
Однополостный гиперболоид график и уравнение

5. Аналогично будет выглядеть формула для вычисления второй функции. (См. рис. 2)

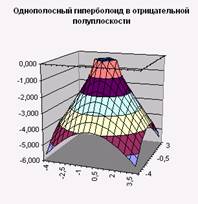
6. Постройте поверхности, выбрав диаграмму под названием «Поверхность» (Рис. 3, Рис. 4).

Задание 2. Постройте двуполостный гиперболоид

На Листе 3 постройте поверхность, представляемую уравнением

Такая поверхность называется двуполостный гиперболоид.

В таблице для вычисления первой функции (Рис. 5) приведена формула, которую следует скопировать по строкам и столбцам.

Аналогично будет выглядеть формула для вычислений второй функции. (См. рис. 6)

Видео:Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Гиперболоиды: однополостный и двуполостный

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Определение гиперболоида

Однополостным гиперболоидом называется поверхность, определяемая в некоторой прямоугольной системе координат каноническим уравнением

Двуполостным гиперболоидом называется поверхность, определяемая в некоторой прямоугольной системе координат каноническим уравнением

В уравнениях (4.48), (4.49) — положительные параметры, характеризующие гиперболоиды, причем .

Начало координат называют центром гиперболоида. Точки пересечения гиперболоида с координатными осями называются его вершинами. Это четыре точки однополостного гиперболоида (4.48) и две точки двуполостного гиперболоида (4.49). Три отрезка координатных осей, соединяющих вершины гиперболоидов, называются осями гиперболоидов. Оси гиперболоидов, принадлежащие координатным осям , называются поперечными осями гиперболоидов, а ось, принадлежащая оси аппликат , — продольной осью гиперболоидов. Числа , равные половинам длин осей, называются полуосями гиперболоидов.

Видео:Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Плоские сечения однополостного гиперболоида

Подставляя в уравнение (4.48), получаем уравнение линии пересечения однополостного гиперболоида с координатной плоскостью . Это уравнение в плоскости определяет эллипс, который называется горловым. Линии пересечения однополостного гиперболоида с другими координатными плоскостями являются гиперболами. Они называются главными гиперболами. Например, при получаем главную гиперболу , а при — главную гиперболу

Рассмотрим теперь сечение однополостного гиперболоида плоскостями, параллельными плоскости . Подставляя , где — произвольная постоянная (параметр), в уравнение (4.48), получаем

При любом значении параметра уравнение определяет эллипс с полуосями . Следовательно, сечение однополостного гиперболоида плоскостью представляет собой эллипс, центр которого лежит на оси аппликат, а вершины — на главных гиперболах. Среди всех эллипсов, получающихся в сечениях плоскостями при различных значениях параметра , горловой эллипс (при ) является эллипсом с наименьшими полуосями.

Таким образом, однополостный гиперболоид можно представить как поверхность, образованную эллипсами, вершины которых лежат на главных гиперболах (рис.4.42,а)

Видео:Поверхности в Excel (Surface in Excel)Скачать

Плоские сечения двуполостного гиперболоида

Сечения двуполостного гиперболоида координатными плоскостями и представляют собой гиперболы (главные гиперболы).

Рассмотрим теперь сечения двуполостного гиперболоида плоскостями, параллельными плоскости . Подставляя , где — произвольная постоянная (параметр), в уравнение (4.49), получаем

При уравнение не имеет действительных решений (правая часть уравнения отрицательная, а левая неотрицательная), т.е. плоскость не пересекает двуполостный гиперболоид. При уравнение имеет нулевое решение . Следовательно, плоскости касаются двуполостного гиперболоида в его вершинах . При c» png;base64,iVBORw0KGgoAAAANSUhEUgAAADoAAAAVBAMAAADlb+D4AAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADnRSTlMAg0KoBP0QXdEhwHEx4v6hyb4AAADaSURBVCjPY2DAD/ZAae4D2GSFGBiqlgNpRgUcsofD8ckyh+GT5W2Ay1piyk4VgMtOXoQhW1q9WAFm8uTlMAn2VWZgWdMm5gtweye3Q2i25mkXwbJXJzDGIFyVCJHOaGAMBMlyBjIwByC5OfEiiBQtYFMAybKHM7AaIMmmN4LIUKirgN49ugHJ5O4EEBUFleVtYBHNMYDJToS6KpiBgRMkmyrAsIL5AMxHUEkGCwY2c5CsqgLDXnOM0MhaaAx2FQ/QjASILJsRIpiSEiBhBQY4Y4Fs2U2wlINFFgCrpSqpbSiUhgAAAABJRU5ErkJggg==» style=»vertical-align: middle;» /> получаем уравнение эллипса с полуосями . Следовательно, сечение двуполостного гиперболоида плоскостью при c» png;base64,iVBORw0KGgoAAAANSUhEUgAAADoAAAAVBAMAAADlb+D4AAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADnRSTlMAg0KoBP0QXdEhwHEx4v6hyb4AAADaSURBVCjPY2DAD/ZAae4D2GSFGBiqlgNpRgUcsofD8ckyh+GT5W2Ay1piyk4VgMtOXoQhW1q9WAFm8uTlMAn2VWZgWdMm5gtweye3Q2i25mkXwbJXJzDGIFyVCJHOaGAMBMlyBjIwByC5OfEiiBQtYFMAybKHM7AaIMmmN4LIUKirgN49ugHJ5O4EEBUFleVtYBHNMYDJToS6KpiBgRMkmyrAsIL5AMxHUEkGCwY2c5CsqgLDXnOM0MhaaAx2FQ/QjASILJsRIpiSEiBhBQY4Y4Fs2U2wlINFFgCrpSqpbSiUhgAAAABJRU5ErkJggg==» style=»vertical-align: middle;» /> представляет собой эллипс с центром на оси аппликат, вершины которого лежат на главных гиперболах.

Таким образом, двуполостный гиперболоид можно представить как поверхность образованную эллипсами, вершины которых лежат на главных гиперболах (рис.4.43,а).

Видео:Лекция. Гиперболоиды, параболоиды, конус. Исследование методом сечений.Скачать

Гиперболоиды вращения

Гиперболоид, у которого поперечные полуоси равны , называется гиперболоидом вращения . Такой гиперболоид является поверхностью вращения, а его сечения плоскостями (для двуполостного гиперболоида при c» png;base64,iVBORw0KGgoAAAANSUhEUgAAADoAAAAVBAMAAADlb+D4AAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADnRSTlMAg0KoBP0QXdEhwHEx4v6hyb4AAADaSURBVCjPY2DAD/ZAae4D2GSFGBiqlgNpRgUcsofD8ckyh+GT5W2Ay1piyk4VgMtOXoQhW1q9WAFm8uTlMAn2VWZgWdMm5gtweye3Q2i25mkXwbJXJzDGIFyVCJHOaGAMBMlyBjIwByC5OfEiiBQtYFMAybKHM7AaIMmmN4LIUKirgN49ugHJ5O4EEBUFleVtYBHNMYDJToS6KpiBgRMkmyrAsIL5AMxHUEkGCwY2c5CsqgLDXnOM0MhaaAx2FQ/QjASILJsRIpiSEiBhBQY4Y4Fs2U2wlINFFgCrpSqpbSiUhgAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />) представляют собой окружности с центрами на оси аппликат. Однополостный или двуполостный гиперболоиды можно получить, вращая вокруг оси гиперболу (рис.4.42,б) или сопряженную гиперболу (рис.4.43,б) соответственно. Заметим, что уравнение последней можно записать в форме .

Гиперболоид, у которого поперечные оси различны , называется трехосным (или общим).

1. Плоскости определяют в пространстве основной прямоугольный параллелепипед , вне которого находится двуполостный гиперболоид (рис.4.43,в). Две грани параллелепипеда касаются гиперболоида в его вершинах.

2. Сечение однополостного гиперболоида плоскостью, параллельной оси аппликат и имеющей одну общую точку с горловым эллипсом (т.е. касающейся его), представляет собой две прямые, пересекающиеся в точке касания. Например, подставляя в уравнение (4.48), получаем уравнение двух пересекающихся прямых (см. рис.4.42,а).

3. Однополостный гиперболоид является линейчатой поверхностью, т.е. поверхностью, образованной движением прямой (см. рис.4.42,в). Например, однополостный гиперболоид вращения можно получить, вращая прямую вокруг другой прямой, скрещивающейся с ней (но не перпендикулярной).

4. Начало канонической системы координат является центром симметрии гиперболоида, координатные оси — осями симметрии гиперболоида, координатные плоскости — плоскостями симметрии гиперболоида.

В самом деле, если точка принадлежит гиперболоиду, то точки с координатами при любом выборе знаков также принадлежат гиперболоиду, поскольку их координаты удовлетворяют уравнению (4.48) или (4.49) соответственно.