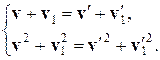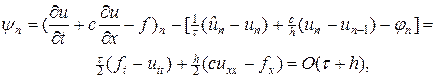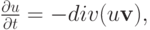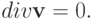При классификации уравнений с частными производными (2.1) отмечалось, что уравнения первого порядка называются также уравнениями переноса. Это объясняется тем, что такие уравнения описывают процессы переноса частиц в средах, распространения возмущений и т.п.
В общем случае уравнения переноса могут иметь значительно более сложный вид (например, интегродифференциальное уравнение Больцмана в кинетической теории газов). Однако здесь мы ограничимся линейным уравнением с частными производными первого порядка. Его решение представляет интерес не только с практической точки зрения; в еще большей степени это уравнение полезно при разработке и исследовании разностных схем.
Будем считать, что искомая функция Uзависит от времени tи одной пространственной переменной х. Тогда линейное уравнение переноса может быть записано в виде
(2.23)
Здесь а — скорость переноса, которую будем считать постоянной и положительной. Это соответствует переносу (распространению возмущений) слева направо в положительном направлении оси х. Правая часть F(x, t) характеризует наличие поглощения (или, наоборот, источников) энергии, частиц и т.п. в зависимости от того, какой физический процесс описывается уравнением переноса.
Характеристики уравнения (2.23) определяются соотношениями х — at = С = const. При постоянном а они являются прямыми линиями, которые в данном случае (а > 0) наклонены вправо (рис. 2.5).
Рис. 2.5. Область решения
Расчетная область при решении уравнения (2.23) может быть как бесконечной, так и ограниченной. В первом случае, задавая начальное условие при t = 0:
(2.24)
получаем задачу Коши для полуплоскости 
На практикеобычно приходится решать уравнение переноса в некоторой ограниченной области (например, в прямоугольнике 
; см. рис. 2.5). Начальное условие (2.24) в этом случае задается на отрезке l1; граничное условие нужно задать при х = 0, т.е. на отрезке l2, поскольку при а > 0 возмущения распространяются вправо. Это условие запишем в виде
(2.25)
Таким образом, задача состоит в решении уравнения (2.23) с начальным и граничным условиями (2.24) и (2.25) в ограниченной области G: 
Убедиться в том, что данная задача поставлена правильно (корректно) можно, проанализировав решение уравнения (2.23), которое при F(x, t) = 0 имеет вид
(2.26)
где Н — произвольная дифференцируемая функция. В этом легко убедиться, подставляя (2.26) в уравнение (2.23). Решение (2.26) называется бегущей волной (со скоростью а). Это решение постоянно вдоль каждой характеристики: при х — at = С искомая функция U = Н(х — at) = Н(С) постоянна. Таким образом, начальные и граничные условия переносятся вдоль характеристик, поэтому они должны задаваться на отрезках l1и l2 расчетной области G(см. рис. 2.5).
Можно также построить аналитическое решение задачи Коши для неоднородного уравнения (2.23). Заметим лишь, что решение этой задачи меняется вдоль характеристики, а не является постоянным.
Рассмотрим разностные схемы для решения задачи (2.23) — (2.25). Построим в области Gравномерную прямоугольную сетку с помощью прямых xi = ih (i =0,1. I) и 
. Вместо функций U(x,t), F(x,t), Ф(х) и 
будем рассматривать сеточные функции, значения которых в узлах (xi, tj) соответственно равны 
и 
. Для построения разностной схемы необходимо выбрать шаблон. Примем его в виде правого нижнего уголка(рис. 2.6). При этом входящие в уравнение (2.23) производные аппроксимируются конечно-разностными соотношениями с использованием односторонних разностей:
(2.27)
Рис. 2.6. Правый нижний уголок
Решая это разностное уравнение относительно единственного неизвестного значения 
на (j + 1)-ом слое, получаем следующую разностную схему:
(2.28)
Полученная схема явная, поскольку значения сеточной функции в каждом узле верхнего слоя 
выражаются явно с помощью соотношений (2.28) через ранее найденные ее значения на предыдущем слое.
Для начала счета по схеме (2.28), т.е. для вычисления сеточной функции на первом слое, необходимы ее значения на слое j= 0. Они определяются начальным условием (2.24), которое записываем для сеточной функции:
(2.29)
Граничное условие (2.25) также записывается в сеточном виде:
(2.30)
Таким образом, решение исходной дифференциальной задачи (2.23) — (2.25) сводится к решению разностной задачи (2.28) – (2.30). Найденные значения сеточной функции 
принимаются в качестве значений искомой функции и в узлах сетки.
Алгоритм решения исходной задачи (2.23) — (2.25) с применением рассмотренной разностной схемы достаточно прост. На рис. 2.7 представлена его структурограмма. В соответствии с этим алгоритмом в памяти компьютера хранится весь двумерный массив , и он целиком выводится на печать по окончании счета. С целью экономии памяти (и если эти результаты не понадобятся для дальнейшей обработки) можно воспользоваться тем, что схема двухслойная, и хранить лишь значения сеточной функции на двух соседних слоях 
. Рекомендуем читателю соответственным образом модифицировать представленный алгоритм и построить новую структурограмму.
Рис. 2.7. Алгоритм решения линейного уравнения переноса
Укажем теперь некоторые свойства данной разностной схемы. Она аппроксимирует исходную задачу с первым порядком, т.е. невязка имеет порядок O(h+τ). Схема условно устойчива; условие устойчивости имеет вид
(2.31)
Эти свойства схемы установлены в предположении, что решение U(x, t), начальное и граничное значения Ф(х) и 
дважды непрерывно дифференцируемы, а правая часть F(x, t) имеет непрерывные первые производные.
Поскольку схема (2.28) устойчива и аппроксимирует исходную задачу, то в соответствии с приведенной в разд. 2.1 теоремой сеточное решение сходится к точному с первым порядком при 
. Отметим, что при а 0 эта схема не сходится.
Граничное условие для уравнения переноса (2.23) при а 0). Такая аппроксимация называется противопотоковой и широко используется при численном решении уравнений переноса.
При построении явной разностной схемы (2.28) производная ¶U/¶х аппроксимировалась с помощью значений сеточной функции на j-ом слое; в результате получилось разностное уравнение (2.27), в котором использовано значение сеточной функции 
лишь в одном узле верхнего слоя. Если производную¶U/¶х аппроксимировать на (j + 1)-ом слое (шаблон изображен на рис. 2.9), то получится неявная схема. Разностное уравнение примет вид
(2.34)
Рис. 2.9. Правый верхний уголок
Разрешая это уравнение относительно 
, приходим к следующей разностной схеме:
(2.35)
Это двухслойная трехточечная схема первого порядка точности. Она безусловно устойчива (при а > 0). Хотя формально данная разностная схема строилась как неявная, практическая организация счета по ней проводится так же, как и для явных схем.
Действительно, в правую часть уравнения (2.35) входит значение 
на (j+1)-ом слое, которое при вычислении 
уже найдено. При расчете 
значение 
берется из граничного условия (2.30). По объему вычислений и логике программы (см. рис. 2.7) схема (2.35) аналогична схеме (2.28), однако безусловная устойчивость делает ее более удобной, поскольку исключается ограничение на величину шага.
Схему (2.28) можно применять для решения задачи Коши в неограниченной области, поскольку граничное условие (2.30) в этой схеме можно не использовать.
Рис. 2.10. Прямоугольник
Рассмотрим еще одну разностную схему, которую построим на симметричном прямоугольном шаблоне (рис. 2.10). Производная по tздесь аппроксимируется в виде полусуммы отношений односторонних конечных разностей в (i — 1)-м и i-м узлах, а производная по x — в виде полусуммы конечно-разностных соотношений на j—ми (j + 1)-ом слоях. Правую часть вычисляют в центре ячейки, хотя возможны и другие способы ее вычисления (например, в виде некоторой комбинации ее значений в узлах). В результате указанных аппроксимаций получим разностное уравнение в виде
(2.36)
Данная двухслойная четырехточечная схема также формально построена как неявная. Однако из (2.36) можно выразить неизвестное значение 
через остальные, которые предполагаются известными:
(2.37)
Построенная схема имеет второй порядок точности. Она устойчива на достаточно гладких решениях.
Схема (2.37) получена для случая а > 0. Аналогичную ей схему при а 0, а2 > 0 — скорости переноса вдоль осей х, у, (2.39) — начальное условие при t= 0; (2.40) — граничные условия при х =0, y= 0.
В трехмерной области (х, у, t) построим разностную сетку, ячейки которой имеют форму прямоугольного параллелепипеда. Для этого проведем координатные плоскости через точки деления осей х, у, t:
Значение сеточной функции в узле (i, j, k), с помощью которой аппроксимируются значения 
, обозначим через 
. Построим безусловно устойчивую разностную схему первого порядка точности, аналогичную схеме (2.35). Шаблон изображен на рис. 2.11, где выделена одна ячейка разностной сетки. Сплошными линиями соединены узлы шаблона. Нижний слой (нижнее основание параллелепипеда) имеет номер k, верхний k+ 1.
Рис. 2.11. Шаблон для двумерного уравнения
По аналогии с (2.34) запишем разностное уравнение, аппроксимирующее дифференциальное уравнение (2.38):
Разрешим это уравнение относительно значения сеточной функции в узле 
:
(2.41)
Вычислительный алгоритм этой схемы аналогичен алгоритму одномерной схемы (2.35). Здесь также счет производится по слоям k= 1,2. К. При k= 0 используется начальное условие (2.39), которое нужно переписать в разностном виде:
(2.42)
На каждом слое последовательно вычисляют значения сеточной функции в узлах. При этом последовательность перехода от узла к узлу может быть различной: двигаются параллельно либо оси х, либо оси у. Во втором случае последовательность вычисляемых значений следующая: 
На рис. 2.12 показана нумерация узлов, соответствующая данной последовательности вычислений на каждом временном слое. Точками отмечены расчетные узлы сетки, крестиками — граничные узлы, в которых значения сеточной функции задаются граничными условиями (2.40). Эти условия обходимо записать в сеточном виде:
. (2.43)
Рис. 2.12. Последовательность вычислений
При этом значения 
в угловой точке (х = 0, у = 0) в данной разностной схеме не используются.
Алгоритм решения смешанной задачи (2.38 – 2.40) для двумерного уравнения переноса по схеме (2.41) с учетом сеточных начального и граничных условий (2.42) и (2.43) представлен на рис. 2.13. При этом некоторые блоки (вычисление начальных значений uij, значений на границе 
пересылка 
) даны схематически, хотя каждый из них представляет циклический алгоритм.
Рис. 2.13. Алгоритм решения двумерного уравнения переноса
В данном алгоритме предусмотрено хранение в памяти машины не полного трехмерного массива искомых значений 
, а лишь значений на двух слоях: 
— нижний слой, 
— верхний слой (искомые значения). Введен счетчик выдачи l, решение выдается через каждые Lслоев; при L = 1 происходит выдача результатов на каждом слое. Блок «Вычисление » вычисляет искомое значение по формуле, которая в принятых в структурограмме обозначениях имеет вид
Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать
Линейное уравнение переноса
Лекция №10
Уравнение переноса
Линейное уравнение переноса
Задачи описания переноса частиц в веществе весьма разнообразны: это перенос электронов, протонов и нейтронов, перенос гамма излучения, диффузия одного вещества в другом, конвективный перенос в жидкости и в газе и прочие задачи. Задачи подобного типа могут быть сведены к решению нелинейных интегро-дифференциальных уравнений. Например, кинетическая теория газов базируется на уравнении Больцмана, которое имеет следующий вид:
(1)
где 
— функция распределения газа атомов, скорости пары атомов до и после взаимодействия с дифференциальным сечением 
(dw = 2p sinc dc — телесный угол, где c — угол отклонения при взаимодействии пары атомов) удовлетворяют законам сохранения импульса и энергии:
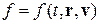
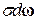
Решение уравнения Больцмана (1) крайне сложно и выходит за пределы данного курса лекций. Ограничимся решением линейного дифференциального уравнения вида:
, (2)
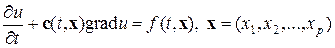
где c — вектор скорости переноса. Многомерность уравнения переноса (2) не вносит ничего принципиально нового, поэтому в дальнейшем будем исследовать одномерное уравнение переноса с постоянной, если не оговорено противное, скоростью c:
. (3)
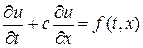
Если правая часть уравнения (3) равна нулю, уравнение можно решить в общем виде, тогда решение выступает в форме бегущей волны
, (4)
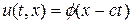
где f = f(x) — произвольная функция. Согласно (4) видно, что параметр c выступает в качестве скорости переноса, причем при c > 0 волна двигается слева направо. Учитывая (4), определим типичные корректные постановки задачи решения уравнения переноса (3).
Смешанная задача Коши. Зададим начальные и граничные условия вида:
(5)
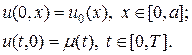
Решение задачи (3), (5) однозначно определено в области G(t,x) = [0,T] ´ [0,a], если начальное и граничное условия непрерывны вместе со своими p-и производными, при этом выполнены условия согласования в точке стыка начальных и граничных условий. Для случая f(t,x) = 0 условия стыковки имеют вид:
,
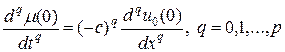
которое следует из точного решения задачи (3), (5):
(6)
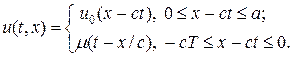
Для случая, когда f(t,x) непрерывна вместе с (p-1)-й производной, то решение u(t,x) непрерывно в G вместе с p-й производной.
Задача Коши. Определим начальные данные на полубесконечной прямой: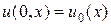 
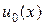
, x Î (-¥,a]. В этом случае решение однозначно определено в области G(t,x) = [0,+¥) ´ (-¥,a]. Гладкость решения соответствует гладкости начального данного 
и правой части f(t,x).
Характеристики уравнения (3) имеют вид x — ct = const и являются прямыми линиями при c = const. Решение (4) однородного уравнения (3) постоянно вдоль характеристики, поэтому говорят, что начальные и граничные условия переносятся вдоль характеристик. На рис.1 приведена иллюстрация такого переноса на примере решения (6). Точка стыка начального и граничного условий развернутая во времени является характеристикой, которая представлена на рис.1 красной стрелкой.
Рис.1. Перенос начального и граничного условия уравнения
переноса по характеристикам
Рассмотрим разностные схемы решения смешанной задачи Коши. Они называются схемами бегущего счета. Схемы бегущего счета легко обобщаются на многомерный случай, они просты и позволяют решать уравнения переноса с различного рода усложнениями.
Для решения задачи (3), (5) в области G(t,x) = [0,T] ´ [0,a] введем равномерную для простоты сетку с шагами t и h по времени и пространству соответственно. Рассмотрим четыре расчетных шаблона, представленных на рис.2.
 |  |  |  |
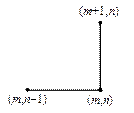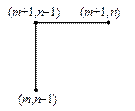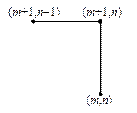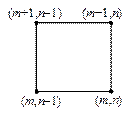| Рис.2,а. Трехточечный шаблон | Рис.2,б. Трехточечный шаблон | Рис.2,в. Трехточечный шаблон | Рис.2,г. Четырехточечный шаблон |
Составим разностные схемы ко всем четырем шаблонам на рис.2.
(7а)
, (7б)
, (7в)
. (7г)
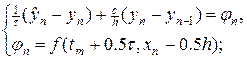
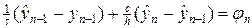
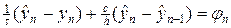
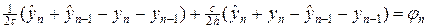
Во всех четырех схемах правая часть выбиралась в центре ячейки. Возможен и другой способ аппроксимации правой части.
Все четыре разностные схемы (7а) — (7г), по существу, являются явными. Во всех схемах значение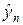 
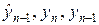
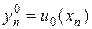
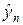
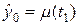
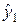
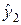
явно выражается через 
. Решение на нулевом слое известно из начального условия, т.е. 
. Для вычисления решения на следующем слое из граничного условия находим 
, это позволяет найти 
, далее вычисляется 
и т.д. Таким образом находится решение на первом слое, аналогично находится решение на втором слое и т.д. Именно в связи с тем, что решение вычисляется слой за слоем слева направо, схемы (7а) — (7г) называются схемами бегущего счета.
Алгоритмы бегущего счета обеспечивают существование и единственность решений при любых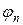 
. Поэтому для доказательства сходимости остается разобраться с аппроксимацией и устойчивостью разностных схем. Поскольку граничное условие воспроизводится точно, постольку исследование устойчивости по нему не требуется.
Разностная схема (7а). Исследуем погрешность аппроксимации схемы (7а). Для этого разложим решение и правую часть в окрестности точки (tm,xn) в ряд Тейлора, считая непрерывность всех требуемых производных:
,
,
.
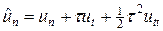
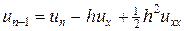
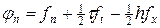
Учитывая эти разложения, находим невязку схемы (7а):
т.е. схема (7а) имеет аппроксимацию первого порядка в норме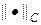 
.
Устойчивость исследуем с помощью принципа максимума, формулировка и доказательство которого приведены в лекции №9. Критерий равномерной устойчивости по начальным данным (формула (64) в лекции №9 при C = 0) дает следующее ограничение:
,
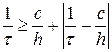
которое сводится к так называемому условию Куранта
Согласно (8), разностная схема (7а) является условно устойчивой© в норме .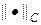
Методом разделения переменных можно доказать необходимость условия (8) для обеспечения устойчивости. Подставим в схему (7а) следующие величины:
,
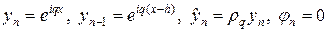
тогда множитель роста гармоники
.
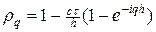
Условие устойчивости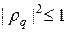 
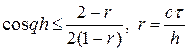
обеспечивается, когда
. (9)
Выполнение неравенства (9) при произвольном q обеспечено, когда r £ 1, т.е. при выполнении условия Куранта. При нарушении условия Куранта, т.е. при r > 1 неравенство (9) не выполняется при всех q, а только при некоторых. Так, при r >> 1 неравенство (9) перепишется в виде: cos qh £ ½, т.е. амплитуды некоторых гармоник растут при переходе со слоя на слой и схема неустойчива по начальным данным.
Устойчивость по правой части согласно формуле (65) лекции №9 обеспечивается при k = 1 в норме 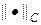, когда верно условие Куранта.
В итоге схема (7а) при выполнении условия Куранта сходится в 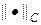с первым порядком точности.
В качестве примера рассмотрим численное решение задачи
(10)
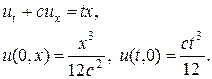
Задача (10) имеет следующее аналитическое решение:
(11)
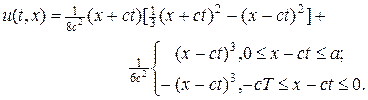
На листинге_№1 приведен код программы численного решения задачи (10) по разностной схеме (7а). На рис.3,а приведено трехмерное изображение решения u(t,x) при выполнении условия Куранта, а на рис.3,б приведено решение при нарушении условия Куранта. Видно, появление неустойчивости в решении при нарушении условия (8).
%Программа численного решения уравнения
%очищаем рабочее пространство
%определяем параметр скорости переноса c,
%а также отрезок времени интегрирования T и
%диапазон изменения пространственной
%определяем шаг по пространству
%рассматривается два варианта расчета
%при tau=h/c (условие Куранта выполняется) и
%при tau=1.12*h/c (условие Куранта нарушено)
%определяем сетки по времени и по пространству
%определяем начальное значение u(0,x)=x^3/(12c^2)
%организуем расчет по разностной схеме (7а)
%определяем левое граничное значение
%рисуем численное решение уравнения переноса u(t,x)
surf(ti,xi,y); [xi ti]=meshgrid(x,t);
%рисуем численное решение уравнения переноса u(t,x)
 |  |
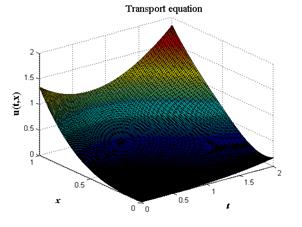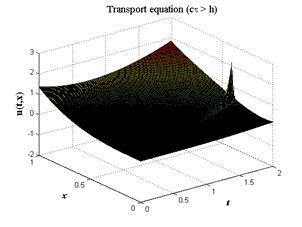| Рис.3,а. Численное решение уравнения (10) по разностной схеме (7а) при выполнении условия Куранта | Рис.3,б. Численное решение уравнения (10) по разностной схеме (7а) с нарушением условия Куранта (8) |
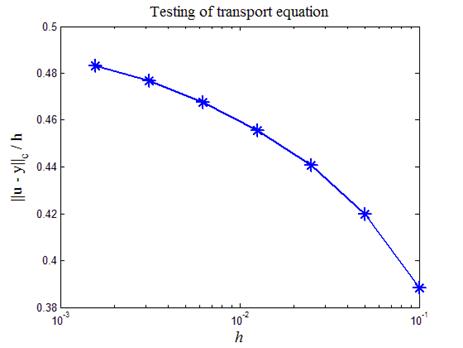
Сравним теперь численное решение задачи (10) и аналитическое решение (11). На листинге_№2 приведен код соответствующей программы. В программе считается, что t = 0.5h/c и варьируется шаг по пространству. На рис.4 приведен итог работы кода программы листинга_№2 в виде кривой зависимости отношения ошибки численного решения к шагу сетки const(h) =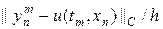 
в зависимости от шага сетки h. Из условия аппроксимации разностной схемой (7а) исходного уравнения (3) с порядком O(t + h) следует, что величина const(h) должна стремиться к некоторой константе по мере того, как h ® 0. Такая тенденция видна на рис.4.
%Программа численного решения уравнения
%сравнение его с аналитическим решением
%определяем параметр скорости переноса c,
%а также отрезок времени интегрирования T и
%диапазон изменения пространственной
%определяем количество делений шага h пополам
%делим шаг h пополам
%определяем шаг по времени, который считается
%пропорциональным шагу по пространству
%определяем сетки по времени и по пространству
%определяем начальное значение u(0,x)=x^3/(12c^2)
%организуем расчет по разностной схеме (7а)
%определяем левое граничное значение
%определяем ошибку численного решения в норме C
%и делим ее на шаг сетки h
%рисуем зависимость предстепенной константы от
%функция, возвращающая аналитическое решение
Разностная схема (7б) исследуется аналогично. Для исследования аппроксимации разложение в ряд Тейлора удобно проводить в окрестности узла (xn —1,tm + t). Для дважды непрерывно дифференцируемого решения данная схема при выполнении условия устойчивости
обеспечивает сходимость со скоростью O(t + h).
Разностная схема (7в) безусловно устойчива и на дважды непрерывно дифференцируемых решениях сходится к точному решению со скоростью O(t + h).
Разностная схема (7г) симметричная и следует ожидать, что порядок ее аппроксимации выше, чем в предыдущих членах. Для оценки порядка аппроксимации разложение в ряд Тейлора удобно провести в окрестности центра ячейки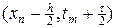 
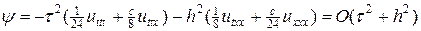
. После проведения соответствующих выкладок, можно найти оценку невязки:
. (13)
Тем самым схема (7г) имеет второй порядок аппроксимации, когда решения имеют непрерывные производные вплоть до третьей.
Рис.4. Зависимость предстепенной константы в оценке ошибки
численного решения от шага сетки
Устойчивость разностной схемы (7г) исследуем с помощью метода разделения переменных. Подставляя в (7г)
,
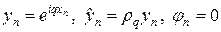
найдем значение коэффициента роста Фурье-гармоники при переходе со слоя на слой:
. (14)
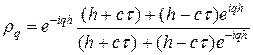
Из оценки (14) следует, что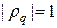 
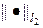
для любой гармоники и при любых соотношениях шагов. Это означает, что схема (7г) безусловно и равномерно устойчива по начальным данным в норме 
.
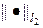
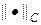
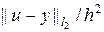
Исследуем разностную схему (7г) на предмет сходимости в двух нормах: и . На листинге_№3 приведен код программы для изучения сходимости схемы (7г) на примере численного решения задачи (10) и сравнения полученного решения с аналитическим решением (11). В программе вычисляются зависимости предстепенных констант const(h) для двух норм от шага сетки h, при этом считается, что t = 0.5h/c. Согласно теоретическим оценками, предстепенная константа const(h) = 
должна выходить на некоторое постоянное значение при h ® 0.
%Программа численного решения уравнения
%сравнение его с аналитическим решением
%определяем параметр скорости переноса c,
%а также отрезок времени интегрирования T и
%диапазон изменения пространственной
%определяем количество делений шага h пополам
%делим шаг h пополам
%определяем шаг по времени, который считается
%пропорциональным шагу по пространству
%определяем сетки по времени и по пространству
%определяем начальное значение u(0,x)=x^3/(12c^2)
%организуем расчет по разностной схеме (7г)
Видео:Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать
Численные методы решения уравнений в частных производных гиперболического типа (на примере уравнения переноса)
3.1. Простейшее линейное уравнение переноса
Рассмотрим простейший пример уравнений в частных производных . Пусть в некотором объеме движущейся жидкости находится пассивная примесь, т.е. такая, наличие которой не меняет принципиально характер движения. Например, это может быть маркер — краска, чернила или мелкие частицы, которые специально добавлены в жидкость для визуализации течений. Тогда изменение концентрации примеси в любом сколь угодно малом объеме равно потоку примеси через границы объема в единицу времени (закон сохранения массы), и можно записать, устремляя рассматриваемый объем к нулю
где u — концентрация пассивной примеси, 
— скорость течения жидкости. Пусть жидкость несжимаема и
Тогда из двух предыдущих соотношений сразу следует уравнение
 | ( 3.1) |
Равенство (3.1) будем в дальнейшем называть уравнением переноса пассивной примеси или линейным уравнением переноса . Кроме (3.1), будем рассматривать и одномерное уравнение переноса
 | ( 3.2) |
а также неоднородное уравнение переноса
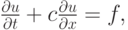 | ( 3.3) |
где f — заданная функция , играющая роль источника ( стока ).
Неоднородным уравнением переноса описываются системы, в которых пассивная примесь может вступать, например, в химические реакции. Если уравнения переноса описывают распространение планктона, то в правой части будет стоять функция , описывающая размножение планктона и его пассивную утечку (например, за счет его поедания рыбами). О неоднородных линейных моделях речь пойдет ниже.
Уравнения вида (3.1), (3.2), (3.3) традиционно рассматриваются в курсах обыкновенных дифференциальных уравнений [13.1], [13.2].
Причина этого кроется в следующем обстоятельстве. Рассмотрим систему ОДУ
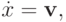 | ( 3.4) |
соответствующую (3.1). Это — уравнение характеристик для линейного уравнения переноса . Если функция u является первым интегралом (3.4), то она является решением (3.1). Иными словами, вдоль характеристики решение однородного уравнения переноса сохраняет постоянное значение .
Упражнение. Найти в явном виде уравнение характеристики для (3.2). В какое уравнение перейдет неоднородное уравнение переноса (3.3) вдоль характеристики ?
Для корректной постановки задач для линейного уравнения переноса начальные и граничные условия необходимо ставить на некоторой гиперповерхности. Так как решение уравнений переноса распространяется вдоль характеристик , то начальная гиперповерхность должна быть трансверсальной ко всем характеристикам (не иметь точек касания с характеристиками ). Кроме того, если для однородного уравнения переноса какая — либо характеристика имеет с начальной гиперповерхностью более одной общей точки, то значения начальной функции во всех этих точках должны быть равны между собой. Все эти условия достаточно очевидны, если вспомнить физический смысл уравнения переноса.
Отметим, что наличие характеристик можно считать условием того, что система имеет гиперболический тип. Так, если система уравнений произвольного порядка n имеет n действительных характеристик , будем называть ее гиперболической. Таким образом, линейное уравнение переноса имеет гиперболический тип.
📸 Видео
Физика - перемещение, скорость и ускорение. Графики движения.Скачать
Равномерное прямолинейное движение - физика 9Скачать
Прямолинейное движение. 10 класс.Скачать
27. Уравнения переносаСкачать
Уравнение движения с постоянным ускорением | Физика 10 класс #6 | ИнфоурокСкачать
Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать
Урок 15. Решение задач на графики движенияСкачать
Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать
9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать
Вычислительная математика 23 Квазилинейное уравнение переносаСкачать
Решение физических задач с помощью дифференциальных уравненийСкачать
Урок 21. Решение задач на относительность движения (одномерный случай)Скачать
Уравнения математической физики. Сухарев М.Б. Лекция №5 05.10.23Скачать
Физика - уравнения равноускоренного движенияСкачать
СВОБОДНОЕ ПАДЕНИЕ ТЕЛ 9 класс ускорение свободного падения формулаСкачать
КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать
Разностное функциональное уравнение решено двумя способами.Скачать
Вывод уравнения неразрывности - Лекция 1Скачать
