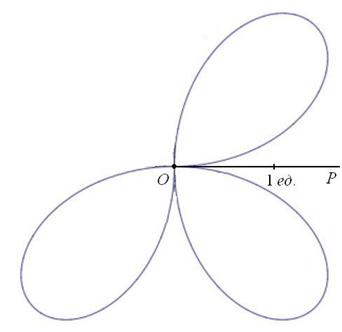
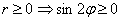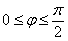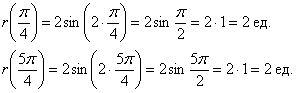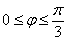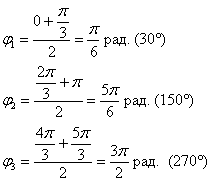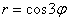Совершенно верно, речь пойдёт о цветке с лепестками:
Построить линии, заданные уравнениями в полярных координатах
а) 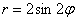
б)
Существует два подхода к построению полярной розы. Сначала пойдём по накатанной колее, считая, что полярный радиус не может быть отрицательным:
Решение:
а) Найдём область определения функции:
Такое тригонометрическое неравенство тоже нетрудно решить графически: из материалов статьи Геометрические преобразования графиков известно, что если аргумент функции удвоить, то её график сожмётся к оси ординат в 2 раза. Пожалуйста, найдите график функции 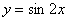
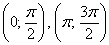
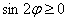
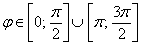
Вообще говоря, решение рассматриваемых неравенств представляет собой бесконечное множество отрезков, но, повторюсь, нас интересует только один период.
Возможно, некоторым читателям более лёгким покажется аналитический способ нахождения области определения, условно назову его «нарезка круглого пирога». Резать будем на равные части и, прежде всего, найдём границы первого куска. Рассуждаем следующим образом: синус неотрицателен, когда его аргумент находится в пределах от 0 до 
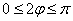
Теперь начинаем последовательно «нарезать равные куски по 90 градусов» против часовой стрелки:
– найденный отрезок 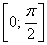
– следующий интервал 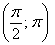
– следующий отрезок 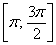
– и, наконец, интервал 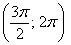
Прямо, как по ромашке – «любит, не любит, любит, не любит» =) С тем отличием, что тут не гадание. Да, прямо какая-то любовь по-китайски получается….
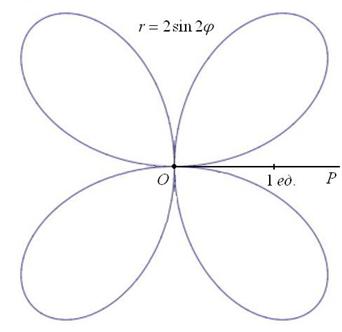
Итак, 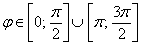
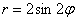
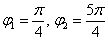
Вот закономерный результат заботливого садовника:
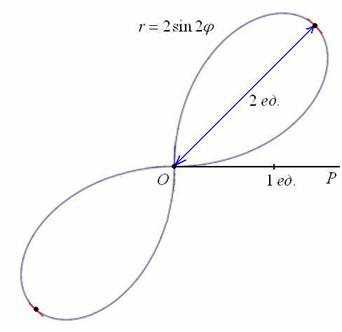
Следует отметить, что длину лепестка легко сразу усмотреть из уравнения 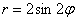
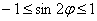
б) Построим линию, заданную уравнением 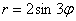
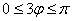
Далее начинаем «нарезку пирога кускам» по 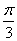
– отрезок 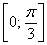
– интервал 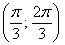
– отрезок 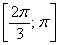
– интервал 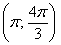
– отрезок 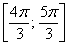
– интервал 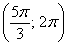
Процесс успешно завершён на отметке 360 градусов.
Таким образом, область определения: 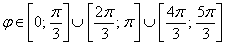
Проводимые действия полностью либо частично несложно осуществлять и мысленно.
Построение. Если в предыдущем пункте всё благополучно обошлось прямыми углами и углами в 45 градусов, то здесь придётся немного повозиться. Найдём вершины лепестков. Их длина 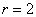
Обратите внимание, что между вершинами лепестков должны обязательно получиться равные промежутки, в данном случае 120 градусов.
Чертёж желательно разметить на 60-градусные секторы (отграничены зелёными линиями) и провести направления вершин лепестков (серые линии). Сами вершины удобно наметить с помощью циркуля – единожды отмерять расстояние в 2 единицы и нанести три засечки на прочерченных направлениях в 30, 150 и 270 градусов:
Готово. Понимаю, что занятие хлопотное, но если хотите всё оформить по уму, то придётся потратить время.
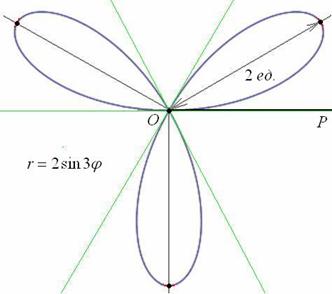
Сформулируем общую формулу: уравнение вида 


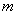
Например, уравнение 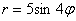
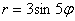
О втором подходе я хотел вообще умолчать, однако не могу пройти мимо – уж слишком он распространён. Суть состоит в том, что полярная роза часто рассматривается в обобщённых полярных координатах, где полярный радиус может быть отрицательным. Вопрос области определения отпадает, но появляются другие приколы.
Во-первых, разберёмся, как строить точки с отрицательным значением «эр». Если 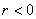
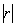
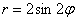
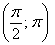
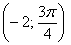
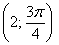
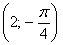
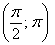
И, соответственно, когда угол проходит значения 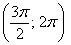
Интересно отметить, что при таком подходе вторая полярная роза 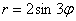
Сформулируем правило розы для обобщенной системы координат: уравнение вида 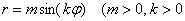

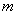
1) если 
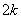
2) если 

Например, роза 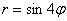
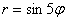
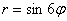
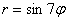
А почему закономерность столь необычна, я только что проиллюстрировал геометрически.
Какой способ выбрать, решать вам, …но я бы не особо рекомендовал использовать обобщенные полярные координаты – у преподавателя могут появиться дополнительные вопросы на счет отрицательных значений полярного радиуса (а то и вообще всё будет забраковано по этой причине)
Короткая задача для самостоятельного решения:
Построить линии, заданные уравнением в полярных координатах
а) 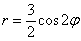
б)
Сформулировать общее правило о количестве и длине лепестков полярной розы вида 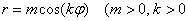

В моём образце решение проведено 1-ым способом. Повторим порядок действий:
– Сначала находим область определения. При этом для лучшего понимания своих действий рекомендую соотносить аналитический способ «нарезки» с графической интерпретацией. По материалам урока Геометрические преобразования графиков выясните, как выглядят, и при необходимости начертите графики функций 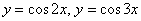
– Находим угловые координаты вершин лепестков – они расположены ровно посередине промежутков области определения.
– Выполняем чертёж. Пойдёт схематическая версия, однако желательно разметить найдённые секторы и угловые направления вершин лепестков (в случае необходимости – с помощью транспортира). Вершины удобно засекать циркулем, предварительно установив раствор, равный длине лепестка.
Существуют более солидные и общие формулы окружности, полярной розы и желающие могут с ними ознакомиться в других источниках информации. Я лишь ограничился практически значимыми (с моей точки зрения) примерами.
Предлагаю перейти ко 2-ой части занятия под названием Как построить линию в полярной системе координат?, где мы продолжим рассматривать типовые задачи, и усовершенствуем свои навыки.
Решения и ответы:
Пример 3: Решение: найдём область определения:
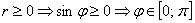
Вычислим полярные координаты точек, принадлежащих данной линии:
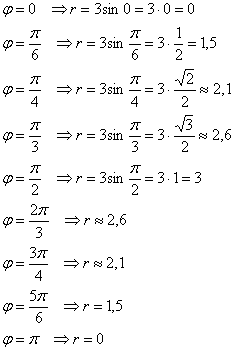
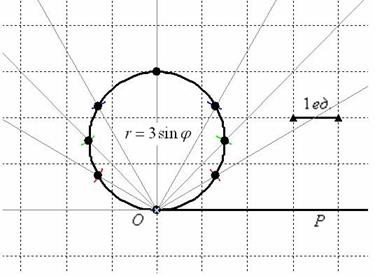
Выполним чертёж:
Найдём уравнение линии в декартовой системе координат:
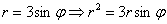
Проведём замены 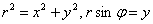
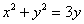
Выделим полный квадрат:
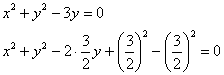
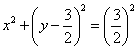
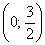
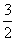
Дополнительная информация: уравнение вида 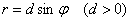
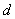
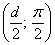
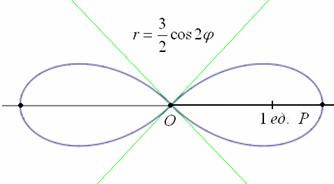
Пример 5: Решение:
а) Найдём область определения: косинус неотрицателен, когда его аргументнаходится в пределах от 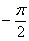
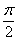
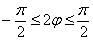
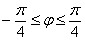
Таким образом:
– отрезок 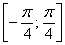
– интервал 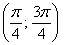
– отрезок 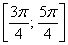
– интервал 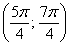
Область определения: 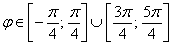
Роза имеет два лепестка, вершины которых находятся на полярной оси и её продолжении, длина лепестка равна 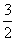
б) область определения: 
Выполним чертёж:
Уравнение вида 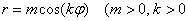


Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Видео:Построение кривой в полярной системе координатСкачать

Уравнения кривых. Роза.
Роза — плоская кривая, ее чертеж схож с рисунком цветка. Эта кривая в полярной системе координат характеризуется выражением:
где a и k — константы, обуславливающие размер (a) и численность лепестков (k) выбранной розы.
Вся линия размещена внутри окружности с радиусом а и при k > 1состоит из идентичных по форме и размеру лепестков. Численность лепестков характеризуется величиной k.
При целом k численность лепестков будет k, когда k нечётное и 2 k,- когда чётное.
При дробном k вида k = m /n, где m и n взаимно простые, количество лепестков розы будет m, когда оба числа нечётные и 2m, если хотя бы одно — чётно.
При k иррациональном лепестков бесчисленное множество.
Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

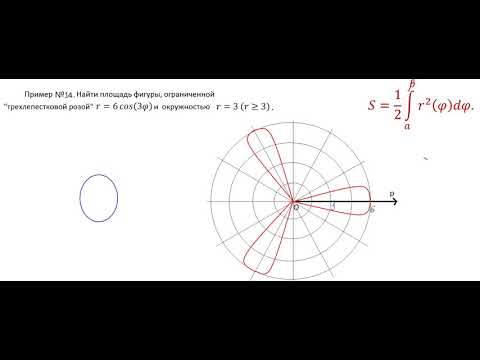
Трехлепестковая роза.
Уравнение имеет вид:
Данное уравнение сходно с линией, образованной вращением против часовой стрелки по кривой 30 o либо π/6 радиан.
В общем, r = acosnθ или r = asinnθ формирует k лепестков когда k — нечетное.
Видео:Площади 12Скачать

Четырехлепестковая роза.
Данное уравнение сходной с линией, образованной вращением против часовой стрелки по кривой 45 o или π/4 радиан.
В общем r = acosnθ или r = asinnθ формирует 2k лепестков если k — четное.
Видео:§7 Розы ГрандиСкачать

СПЕЦИАЛЬНЫЕ ПЛОСКИЕ КРИВЫЕ
ЛЕМНИСКАТЫ
Уравнение в полярных координатах:
r 2 = a 2 cos2θ
Уравнение в прямоугольных координатах:
(x 2 + y 2 ) 2 = a 2 (x 2 — y 2 )
Угол между AB’ или A’B и осью x = 45 o
Площадь одной петли = a 2 /2
ЦИКЛОИДА
Уравнения в параметрической форме:
Площадь одной дуги = 3πa 2
Длина дуги одной арки = 8a
Это кривая, описываемая точкой Р на окружности радиусом а, которая катится вдоль оси х.
ГИПОЦИКЛОИДЫ С ЧЕТЫРЬМЯ ОСТРИЯМИ
Уравнение в прямоугольных координатах:
x 2/3 + y 2/3 = a 2/3
Уравнения в параметрической форме:
Площадь, ограниченная кривой = 3πa 2 /8
Длина дуги целой кривой = 6a
Это кривая, описываемая точкой Р на окружности радиусом a/4, которая катится внутри окружности радиусом a.
КАРДИОИДА
Уравнение: r = a(1 + cosθ)
Площадь, ограниченная кривой = 3πa 2 /2
Длина дуги кривой = 8a
Это кривая, описываемая точкой Р на окружности радиусом a, которая катится снаружи окружности радиусом a. Эта кривая также является частным случаем улитки Паскаля.
ЦЕПНАЯ ЛИНИЯ
Уравнение:
y = a(e x/a + e -x/a )/2 = acosh(x/a)
Это кривая, по которой бы повисла цепь, подвешенная вертикально от точки А к В.
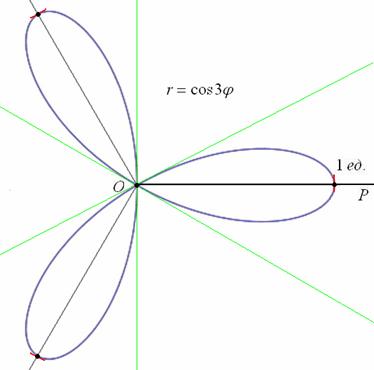
ТРЕХЛЕПЕСТКОВАЯ РОЗА
Уравнение: r = acos3θ
Уравнение r = acos3θ подобно кривой, полученной вращением против часовой стрелки по кривой 30 o или π/6 радиан.
В общем, r = acosnθ или r = asinnθ имеет n лепестков если n является нечетным.
ЧЕТЫРЕХЛЕПЕСТКОВАЯ РОЗА
Уравнение: r = acos2θ
Уравнение r = asin2θ подобно кривой, полученной вращением против часовой стрелки по кривой 45 o или π/4 радиан.
В общем r = acosnθ или r = asinnθ имеет 2n лепестков если n — четное.
ЭПИЦИКЛОИДА
Параметрические уравнения:
Это кривая, описываемая точкой Р на окружности радиуса b, когда она катится по внешней стороне окружности радиусом а. Кардиоида является частным случаем эпициклоиды.
ОБЩАЯ ГИПОЦИКЛОИДА
Параметрические уравнения:
Это кривая, описываемая точкой Р на окружности радиуса b, когда она катится по внешней стороне окружности радиусом а.
Если b = a/4, кривая является гипоциклоидой с четырьмя остриями.
ТРОХОИДА
Параметрические уравнения:
Это кривая, описываемая точкой Р на дистанции b от центра окружности с радиусом а, когда она катится по оси x.
Если b a, кривая имеет форму, показанную на рис. 11-11 и называется троходой.
Если b = a, кривая есть циклоидой.
ТРАКТРИСА
Параметрические уравнения:
Это кривая, описываемая конечной точкой Р натянутой струны длиной PQ, когда другой конец Q перемещается вдоль оси х.
ВЕРЗЬЕРА (ВЕРЗИЕРА) АНЬЕЗИ (ИНОГДА ЛОКОН АНЬЕЗИ)
Уравнение в прямоугольных координатах: y = 8a 3 /(x 2 + 4a 2 )
Параметрические уравнения:
В. На рисунке переменная линия OA пересекающая y = 2a и круг с радиусом a с центром (0,a) в A и B соотвественно. Любая точка P на «локоне» определяется построением линий, параллельных к осям x и y, и через B и A соответственно и определяющие точку пересечения P.
ДЕКАРТОВ ЛИСТ
Уравнение в прямоугольных координатах:
x 3 + y 3 = 3axy
Параметрические уравнения:
Площадь петли 3a 2 /2
Уравнение асимптоты: x + y + a = 0.
ЭВОЛЬВЕНТА ОКРУЖНОСТИ
Параметрические уравнения:
Эта кривая, описанная конечной точкой P струны, когда она разматывается с круга с радиусом a.
ЭВОЛЬВЕНТА ЭЛЛИПСА
Уравнение в прямоугольных координатах:
(ax) 2/3 + (by) 2/3 = (a 2 — b 2 ) 2/3
Параметрические уравнения:
Эта кривая является огибающей нормалью к эллипсу x 2 /a 2 + y 2 /b 2 = 1.
ОВАЛЫ КАССИНИ
Полярное уравнение: r 4 + a 4 — 2a 2 r 2 cos2θ = b 4 .
Это кривая, описываемая такой точкой P, что произведение ее расстояния от двух фиксированных точек [ расстояние 2a в сторону] есть постоянной b 2 .
Кривая, как на фигурах внизу, когда b a соответственно.
Если b = a, кривая есть лемниската
УЛИТКА ПАСКАЛЯ
Полярное уравнение: r = b + acosθ
Пусть OQ будет линией, соединяющей центр O с любой точкой Q на окружности диаметром a проходящей через O. Тогда кривая есть фокусом всех точек P, таких, что PQ = b.
Кривая, показанная на рисунках внизу когда b > a или b 2 = x 3 /(2a — x)
Параметрические уравнения:
Это кривая, описываемая такой точкой P, что расстояние OP = расстоянию RS. Используется в задаче удвоения куба, т.e. нахождения стороны куба, который имеет удвоенный объем заданного куба
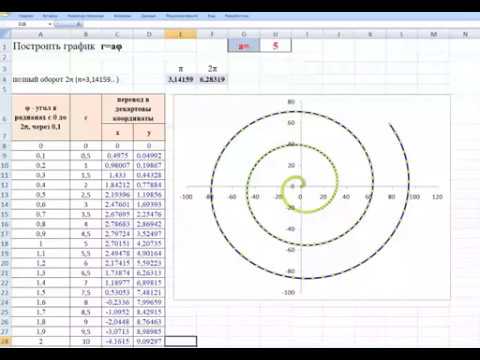
СПИРАЛЬ АРХИМЕДА
Полярное уравнение: r = aθ
📽️ Видео
Роза ветров и график температурыСкачать

Составление розы ветровСкачать

Полярная система координатСкачать

графики спираль Архимера и розы Гранди в ExcelСкачать
§12 Полярное уравнение прямойСкачать

Полярная система координатСкачать

Занятие 01. Часть 3. Полярная система координатСкачать

Видеоурок "Полярная система координат"Скачать

Построение графика функции в полярных координатахСкачать

Полярная система координат.Скачать

Площади 14 1Скачать
Площади полярных роз через двойной интегралСкачать

Полярный график в MathCAD 14 (13/34)Скачать
Площадь фигуры, заданной в полярной системе координатСкачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

§30 Уравнения кривых второго порядка в полярных координатахСкачать