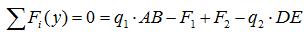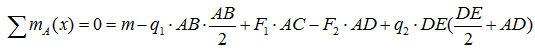Одно из уравнений равновесия для балки показанной на рисунке имеет вид

Видео:Определение опорных реакций в балке (двухопорная балка)Скачать

Определение реакций опор балки – решение задачи

Видео:Определение опорных реакций балки. Сопромат для чайников ;)Скачать

Как определить реакции опор балки

Видео:Определение реакций опор простой рамыСкачать

Пример решения задачи на определение реакций опор балки

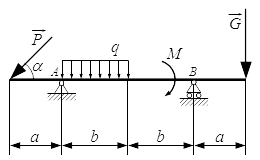
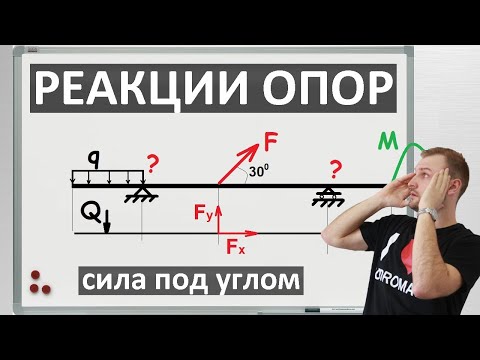
Жесткая балка, линейные размеры которой указаны на рисунке 1, закреплена в точках А и В. На балку действуют пара сил с моментом М, равномерно распределенная нагрузка интенсивностью q и две силы P и G, место приложения которых показано на рисунке.
Определить реакции опор балки в точках A и B, вызываемые указанными нагрузками.

Дано:
P = 20,2 Н ; G = 22,6 Н ; q = 2 Н/м ; M = 42,8 Н·м ; a = 1,3 м ; b = 3,9 м ; α = 45° ;

Решение задачи

Проводим оси x и y системы координат. Начало системы координат поместим в точку A . Ось x направим горизонтально, вдоль балки. Ось y – вертикально. Ось z перпендикулярна плоскости рисунка и направлена на нас. На рисунке она не указана.

Силы, действующие на балку.

Отбрасываем опоры и заменяем их силами реакций.
В шарнире A , разложим силу реакции на составляющие и вдоль осей координат.
Реакция , в подвижной опоре на катках, направлена вертикально. Предполагаемые направления реакций опор выбираем по своему усмотрению, наугад. Если ошибемся с направлением реакции, то получим отрицательное значение, что будет говорить о том, что соответствующая сила реакции направлена в противоположную сторону.

Заменим равномерно распределенную нагрузку q равнодействующей . Абсолютное значение равнодействующей равно площади эпюры:
Н .
Точка приложения равнодействующей находится в центре тяжести эпюры. Поскольку эпюра представляет собой прямоугольник, то ее центр тяжести находится в точке C – посередине отрезка AD :
AC = CD = b/2 = 1,95 м .

Уравнения равновесия для сил

Определяем проекции сил на оси координат.

Разложим силу на составляющие вдоль координатных осей:
.
Абсолютные значения составляющих:
.
Вектор параллелен оси x и направлен в противоположную от нее сторону. Вектор параллелен оси y и также направлен в противоположную сторону. Поэтому проекции силы на оси координат имеют следующие значения:
.

Остальные силы параллельны осям координат. Поэтому они имеют следующие проекции:
;
;
;
;
.

Составляем уравнения равновесия для сил.
Сумма проекций всех сил на ось x равна нулю:
;
;
;
(П1) .

Сумма проекций всех сил на ось y равна нулю:
;
;
;
(П2) .

Уравнения равновесия для моментов

Итак, мы уже составили два уравнения для сил: (П1) и (П2). Но в них есть три неизвестные величины: , и . Чтобы их определить, нам нужно составить еще одно уравнение.

Составим уравнение равновесия для моментов сил. Для этого нам нужно выбрать ось, относительно которой мы будем вычислять моменты. В качестве такой оси возьмем ось, проходящую через точку A , перпендикулярно плоскости рисунка. За положительное направление выберем то, которое направлено на нас. Тогда, по правилу правого винта, положительным направлением закручивания будет направление против часовой стрелки.

Находим моменты сил относительно выбранной оси.
Силы , и пересекают ось. Поэтому их моменты равны нулю:
; ; .

Сила перпендикулярна плечу AB . Ее момент:
.
Поскольку, относительно оси A , сила направлена против часовой стрелки, то ее момент положительный.

Сила перпендикулярна плечу AK . Поскольку, относительно оси A , эта сила направлена по часовой стрелки, то ее момент имеет отрицательное значение:
.

Аналогичным способом находим моменты остальных сил:
;
.
Момент от пары сил M не зависит от точек приложения сил, входящих в пару:
.

Составляем уравнение равновесия. Сумма моментов сил относительно оси A равна нулю:
;

;
;
(П3) .

Решение уравнений равновесия

Итак, для трех неизвестных величин, мы получили три уравнения:
(П1) .
(П2) .
(П3) .

Решаем эти уравнения. Вычисляем расстояния.
м;
м;
м;
м.

Из уравнения (П1) находим:
Н.
Из уравнения (П3) находим:

Н.
Из уравнения (П2) имеем:
Н.
Абсолютное значение реакции опоры в точке A :
Н.

Проверка правильности решения

Чтобы проверить, правильно ли мы определили реакции опор балки, найдем сумму моментов сил относительно другой оси. Если мы нашли реакции правильно, то она должна равняться нулю.

Возьмем ось, проходящую через точку E . Вычисляем сумму моментов сил относительно этой оси:

.
Найдем погрешность вычисления суммы моментов. Найденные силы мы округлили до двух знаков после запятой. То есть погрешность определения реакций опор составляет 0,01 Н . Расстояния, по порядку величины, примерно равны 10 м. Тогда погрешность вычисления суммы моментов составляет около 10·0,01 = 0,1 Нм . Мы получили значение -0,03 Нм . Эта величина отличается от нуля не более, чем на величину погрешности. То есть, с учетом погрешности вычислений, сумма моментов относительно другой оси равна нулю. Значит решение правильное, силы реакций найдены верно.

Второй способ решения

Первым способом мы составили два уравнения для сил и одно – для моментов. Задачу можно решить другим способом, составив два уравнения для моментов и одно для сил.

Воспользуемся тем, что сумма моментов сил равна нулю относительно любой оси. Возьмем вторую ось, которая проходит через точку B перпендикулярно плоскости рисунка. Сумма моментов сил относительно этой равна нулю:
.
Вычисляем моменты сил относительно оси B .
; ; ;
;
;
;
;
.

Сумма моментов сил относительно оси B равна нулю:
;

;
;
(П4) ;

Итак, вторым способом, мы также имеем три уравнения:
(П1) .
(П3) ;
(П4) .

Здесь каждое уравнение содержит только одну неизвестную величину. Реакции и определяются из тех же уравнений, что и ранее. Находим силу из уравнения (П4):

Н.

Значение реакции совпало со значением, полученным первым способом из уравнения (П2).

Автор: Олег Одинцов . Опубликовано: 14-10-2017 Изменено: 28-12-2021

Видео:Определение реакций опор в балке. Сопромат.Скачать

iSopromat.ru

Для плоской системы нагружения, при определении опорных реакций и внутренних силовых факторов исходя из условия равновесия системы, можно составить только три уравнения статики.

Ранее были показаны примеры составления уравнений равновесия для пространственной и плоской систем сил.

При плоском поперечном изгибе можно записать только два уравнения. Это частный случай плоского нагружения. В этом случае все силы приложенные к балке расположены нормально к ее оси, т. е. не дают проекций на ось балки.

В результате имеем следующие уравнения статики:

1. Сумма проекций всех сил на вертикальную ось равна нулю
   
2. Сумма моментов относительно любой точки системы тоже равна нулю.
   

Эти уравнения являются уравнениями равновесия рассматриваемой балки находящейся под действием комплекса нагрузок.

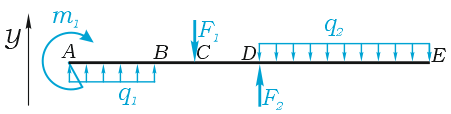
Рассмотрим пример плоского поперечного изгиба, когда все внешние силы имеют исключительно вертикальное направление.

Видео:Термех. Статика. Расчётно-графическая работа по статике №2. Задание 1 и решениеСкачать

Уравнения статики

Сумма проекций всех сил на ось Y:

Здесь силы и нагрузки записаны в соответствии с правилом знаков для проекций сил.

Равнодействующая распределенной нагрузки определяется произведением ее интенсивности на длину.

Проекции сил на ось Z в данном случае равны нулю:

Сумма моментов всех нагрузок, например, относительно точки A :

Видео:Определение опорных реакций в балке. СопроматСкачать

Дополнительные материалы

• Порядок определения момента от распределенной нагрузки.
• Правила знаков при составлении уравнений статики для систем находящихся в равновесии.

Совместное решение системы полученных уравнений позволяет определить величину и направление двух неизвестных усилий.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Определение опорных реакций балки на двух опорахСкачать

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Видео:Определение реакций опор простой рамыСкачать

Задача о равновесии балки

Невесомая горизонтальная балка покоится на опорах A и C. В точке B к ней прикреплен груз массой 20 кг. Расстояние AB = 8 м, BC = 2 м. Найти модули сил, с которыми опоры действуют на балку в точках A и C.

Рассмотрим универсальный алгоритм, позволяющий получить решение для подобных задач. Шаги этого алгоритма делают решение несложным и логически понятным.

Видео:Урок 76. Задачи на правило моментовСкачать

Решение

Чтобы решить предложенную задачу, будем применять:

Обязательно перейдите по ссылкам и ознакомьтесь со статьями. А после продолжайте читать данную статью, цепочка действий для получения ответа станет проще для понимания.

Шаг 1 — составим рисунок

Укажем на рисунке опоры и груз, действующий на балку (рис. 1).

Примечание: Обязательно составляйте рисунок, он поможет ясно увидеть ситуацию задачи

Шаг 2 — заменим тела силами их воздействия

Заменим теперь тела, действующие на балку, силами их воздействия (рис. 2). Каждую опору заменим силой реакции опоры, а груз — силой тяжести.

На рисунке 2 горизонтальными стрелками отмечены плечи сил (mg) и (N_). Точка A выделена красным цветом. Будем считать, что вокруг этой точки балка может вращаться, т. е. через эту точку проходит ось вращения балки.

Примечание: Силы на рисунке 2 направлены вертикально. Поэтому, для составления силового уравнения достаточно провести одну вертикальную ось.

Шаг 3 — составим условия равновесия для балки

Первое условие равновесия балки выглядит так:

( N_ left( H right) ) – сила реакции опоры в точке C;

( mg left( H right) ) – вес (ссылка) груза, прикрепленного к балке в точке B;

Запишем второе условие равновесия балки. Для этого используем точку A, вокруг которой может происходить вращение балки и понятие момента силы.

[ large — N_ cdot AC + mg cdot AB = 0 ]

( AC left( text right) ) – плечо силы реакции опоры (N_);

( mg left( H right) ) – вес груза, прикрепленного к балке в точке B;

Мы получили систему из двух уравнений, описывающих балку, находящуюся в покое под действием приложенных сил.

Решив эту систему, мы найдем две неизвестные силы (N_) и (N_)

Примечание: Сила (mg) вращает рычаг (балку) по часовой стрелке, а сила (N_) — в противоположном направлении. Из-за этого, перед величиной (N_) возникает знак «минус». Подробнее об этом читайте в статье Рычаг, условие равновесия.

Шаг 4 – подставим числовые значения в полученную систему

Масса груза 20 кг. Расстояние AB = 8 м.

Найдем плечо силы (N_) — расстояние AC.

AC = AB + BC — общая длина состоит из длины вех частей балки (смотрите рис. 2)

Подставим числа в систему уравнений для равновесия и получим

Из второго уравнения системы следует, что ( N_ = 160 ) Ньютонов.

Используем этот результат и поместим его в первое уравнение системы. Получаем:

Ответ:

Видео:Определение опорных реакций в простой балке. Урок №1Скачать

Можно ли провести ось вращения через другую точку

Не обязательно в качестве точки, через которую проходит ось вращения, выбирать точку A. Можно для этих целей выбрать, к примеру, точку B (рис. 3).

В таком случае, получим следующую систему уравнений для равновесного положения балки

Решая ее, получим ответ, аналогичный предыдущему случаю.

Если ось вращения проходит через точку C

Мы можем, также, в качестве точки, через которую проходит ось вращения, выбрать точку C (рис. 4).

Система уравнений, описывающих равновесие балки, для этого случая будет выглядеть так

Решение этой системы, также, позволит получить ответ для нашей задачи.

🎦 Видео

определение реакций в стержнях от действия грузовСкачать

РГЗ 2 Статика Балочные системы Определение реакций в опорахСкачать

Определение реакций двухопорной балкиСкачать

Нахождение реакций в двухопорной балке часть 1Скачать

Определение опорных реакций в балкахСкачать

Видеоурок 2. Определение реакций двухопорных балок.Скачать

Балка. Реакции в заделке. Реакции опор. Сопромат.Скачать

Определение реакций опор в жесткой заделке консольной балкиСкачать

БАЛКА С СИЛОЙ ПОД УГЛОМ. Реакции опор. Техническая механикаСкачать

Определение реакций опор составной конструкцииСкачать