Геометрия, 10 класс. Задачник (Е. В. Потоскуев, Л. И. Звавич) 2004

Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Страница № 125.

Учебник: Геометрия. 10 кл.: Задачник для общеобразоват. учреждений с углубл. и профильным изучением математики / Е. В. Потоскуев, Л. И. Звавич. — 2-е изд., стереотип. — М.: Дрофа, 2004. — 256 с.: ил.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

OCR-версия страницы из учебника (текст страницы, которая находится выше):

Чтобы составить уравнение плоскости а, нужно найти коэффициенты А, В, С и свободный член D. Для этого используем условие перпендикулярности точек Р, К иН плоскости а. Так как точкиР,К иН принадлежат плоскости а, то их координаты удовлетворяют уравнению (1), т. е.

Р(2; -1; 2) е а =* А-2 + В • (-1) + С- 2 + D = 0,1 JT(l;-2; 3)е а =>А-1 + В-(-2) + С-3 + D = оЛ Н(- 1;2;0)е а =>А-(-1) + В-2 + С-0 + D = О J

2А — В + 2С + D = О,

А — 2В + ЗС + D = О,

Решая эту систему уравнений, выразим коэффициенты А, В

и С через D:A = , В = , С = . Полагая D = -9, имеем А = 1,В = 5,С = 6, Подставив найденные значения А, В к С в уравнение (1), получаем искомое уравнение плоскости РКН: х + Ъу + 6z — 9 = 0.

7.086. Напишите уравнение плоскости, проходящей через середину отрезка MN и перпендикулярной этому отрезку, если М(-3; 1; 5) и JV(3; 9; -1).

7.087. © Одно из оснований призмы лежит в плоскости 2х — Зу + г — 5 = 0. Напишите уравнение плоскости, в которой лежит другое основание, если одна из вершин призмы имеет координаты (8; 1; 0).

7.088. © Уравнение плоскости Зх + 2у — 6z — 12 = 0 приведите к виду в отрезках.

7.089. Составьте уравнение плоскости, проходящей через точку А(2; -1; 3) и перпендикулярной прямой ВС, если В(—2; 0; 1), С(4; 2; -1).

7.090. Составьте уравнение плоскости, проходящей через точку М(-1; 2; 1) и параллельной плоскости: а) Оху; б)Оуг;

в) Oxz; г) 2х — у + Зг + 5 = 0.

7.091. (Устно.) Найдите точки пересечения плоскости 2х — у + + 2г — 5 = 0 с координатными осями. Напишите уравнение этой плоскости в отрезках.

Учебник: Геометрия. 10 кл.: Задачник для общеобразоват. учреждений с углубл. и профильным изучением математики / Е. В. Потоскуев, Л. И. Звавич. — 2-е изд., стереотип. — М.: Дрофа, 2004. — 256 с.: ил.

Видео:Уравнение плоскости через 3 точкиСкачать

Уравнение плоскости, проходящей через данную точку и параллельной заданной плоскости онлайн

С помощю этого онлайн калькулятора можно найти уравнение плоскости, проходящей через заданную точку и параллельной данной плоскости. Дается подробное решение с пояснениями. Для нахождения уравнения плоскости, введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:Уравнение плоскости. 11 класс.Скачать

Уравнение плоскости, проходящей через данную точку и параллельной заданной плоскости − теория, примеры и решения

Наша задача найти уравнение плоскости, проходящей через точку M₀ и параллельной плоскости (1)(Рис.1).

Все параллельные плоскости имеют коллинеарные нормальные векторы. Поэтому для построения параллельной к (1) плоскости, проходящей через точку M₀(x₀, y₀, z₀) нужно взять в качестве нормального вектора искомой плоскости, нормальный вектор n=(A, B, C) плоскости (1). Далее нужно найти такое значение D, при котором точка M₀(x₀, y₀, z₀) удовлетворяла уравнению плоскости (1):

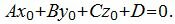(2)

Решим (2) относительно D:

Подставляя значение D из (3) в (1), получим:

Уравнение (4) можно представить также в следующем виде:

Уравнение (5) является уравнением плоскости, проходящей через точку M₀(x₀, y₀, z₀) и параллельной плоскости (1).

Найти уравнение плоскости, проходящей через точку M₀(1, −6, 2) и параллельной плоскости :

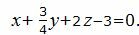(6)

Запишем коэффициенты нормального вектора плоскости (6):

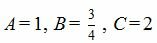(7)

Подставляя координаты точки M₀ и координаты нормального вектора в (3), получим:

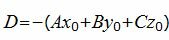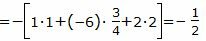(8)

Подставляя значения A, B, C, D в уравнение плоскости (1), получим:

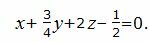Уравнение плоскости можно представить в более упрощенном виде, умножив на 4:

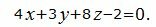Уравнение плоскости, проходящей через точку M₀(1, −6, 2) и параллельной плоскости (6) имеет следующий вид:

Видео:11 класс, 8 урок, Уравнение плоскостиСкачать

4.2.10. Примеры решения задач по теме «Уравнение плоскости в пространстве»

Составить уравнение плоскости, проходящей через точки А=,

Для того, чтобы составить уравнение плоскости, нужно знать координаты

Точки, лежащей в этой плоскости, и координаты нормали, то есть вектора, перпендикулярного плоскости.

Векторы АВ = (-3; 3; -3) и АС = (-6; 2; -2) параллельны данной плоскости, поэтому их векторное произведение или любой вектор, коллинеарный ему, является нормалью к плоскости.

Выберем в качестве нормали П = (0; 1; 1), а точкой <Х0; У0; Z0> будем считать точку В. Тогда уравнение плоскости имеет вид:

Составить канонические уравнения прямой

Для того, чтобы составить канонические или параметрические уравнения прямой в пространстве, нужно знать координаты какой-либо точки, лежащей на этой на этой прямой, и координаты направляющего вектора, то есть вектора, коллинеарного прямой.

Прямая является линией пересечения двух плоскостей, поэтому ее направляющий вектор А параллелен каждой из этих плоскостей и соответственно перпендикулярен нормалям П1 и П2 к данным плоскостям. В таком случае он коллинеарен векторному произведению [N1, N2].

Будем искать точку, лежащую на данной прямой, у которой одна из координат принимает выбранное нами значение; тогда остальные две координаты можно определить единственным образом из системы уравнений, задающей пересекающиеся плоскости. Выберем для удобства вычислений Z0 = 0, тогда для точки М=<Х0; У0; 0>

Теперь составим канонические уравнения данной прямой:

Ответ:

Составить уравнение плоскости, проходящей через прямую L:

Точка А= принадлежит плоскости, соответственно вектор параллелен плоскости. Кроме того, поскольку данная прямая лежит в плоскости, ее направляющий вектор A = (2: 1: -1) параллелен плоскости. Следовательно, нормаль к плоскости коллинеарна векторному произведению этих векторов.

Поскольку прямая лежит в плоскости, ее направляющий вектор A = (2: 1: -1) параллелен плоскости. При T = 0 из уравнений прямой получаем:

Координаты точки А, принадлежащей прямой и соОтВетственно плоскости.

Тогда вектор АМ = (5; -8; 2) параллелен Плоскости. Следовательно, нормаль

П к плоскости коллинеарна векторному произведению [A, AM] = (-6; -9; — 21).

Выберем N = (2; 3; 7) и составим уравнение плоскости, проходящей через

Найти кратчайшее расстояние между прямыми

Координаты направляющих векторов данных прямых A1 = и

A2 = не пропорциональны, следовательно, А1 и А2 не коллинеарны, поэтому прямые либо пересекаются, либо скрещиваются.

Составьте уравнение плоскости A, проходящей через прямую L1 параллельно вектору А2. Если L1 и L2 пересекаются, то прямая L2 будет лежать в этой плоскости; если же L1 и L2 скрещиваются, то L2 параллельна плоскости A, и тогда расстояние между L1 и L2 (длина общего перпендикуляра) будет равно расстоянию от любой точки прямой L2 до плоскости A.

Координаты направляющих векторов данных прямых A1 = и

A2 = не пропорциональны, следовательно, А1 и А2 не коллинеарны, поэтому прямые либо пересекаются, либо скрещиваются.

Составим уравнение плоскости A, проходящей через прямую L1 параллельно вектору А2. Если L1 и L2 пересекаются, то прямая L2 будет лежать в этой плоскости (рис.9); если же L1 и L2 скрещиваются, то L2 параллельна плоскости A, и тогда расстояние между L1 и L2 (длина общего перпендикуляра) будет равно расстоянию от любой точки прямой L2 до плоскости A (рис.10).

[A1, A2] = (10; -14; 1) = N, точка А= лежит на прямой L1, следова-тельно, она лежит и в плоскости A. Тогда уравнение плоскости A имеет вид:

Точка В= принадлежит прямой L2. Проверим, лежит ли эта точка в плоскости A:

Тогда искомой величиной будет расстояние от В до A. Его можно найти, составив нормальное уравнение плоскости A:

Ответ: .

Найти точку, симметричную точке А(5; -10; 4) относительно плоскости

Искомая точка В лежит на прямой, проходящей через точку А перпендикулярно плоскости A так, что ОА = ОВ, где точка О – точка пересечения A с прямой АВ.

Искомая точка В лежит на прямой, проходящей через точку А перпендикулярно плоскости A так, что ОА = ОВ, где точка О – точка пересечения A с прямой АВ. Составим уравнения прямой АВ. Эта прямая перпендикулярна A, поэтому ее направляющим вектором можно считать нормаль к плоскости A: A = N = (1; -3; 1).

Параметрические уравнения прямой АВ имеют вид:

Точка О принадлежит и прямой АВ, и плоскости A, поэтому ее координаты должны удовлетворять и уравнениям прямой, и уравнению плоскости. Подставим в уравнение плоскости A параметрические выражения для X, Y, Z из уравнений прямой АВ:

T + 5 – 3(-3T – 10) + T + 4 – 6 = 0; 11T + 33 = 0; T = -3.

Итак, координаты точки О:

Поскольку точка О – середина отрезка АВ, то

Видео:Найти уравнение плоскости проходящей через прямую и перпендикулярно плоскостиСкачать

4.2.10. Примеры решения задач по теме «Уравнение плоскости в пространстве»

Составить уравнение плоскости, проходящей через точки А=,

Для того, чтобы составить уравнение плоскости, нужно знать координаты

Точки, лежащей в этой плоскости, и координаты нормали, то есть вектора, перпендикулярного плоскости.

Векторы АВ = (-3; 3; -3) и АС = (-6; 2; -2) параллельны данной плоскости, поэтому их векторное произведение или любой вектор, коллинеарный ему, является нормалью к плоскости.

Выберем в качестве нормали П = (0; 1; 1), а точкой <Х0; У0; Z0> будем считать точку В. Тогда уравнение плоскости имеет вид:

Составить канонические уравнения прямой

Для того, чтобы составить канонические или параметрические уравнения прямой в пространстве, нужно знать координаты какой-либо точки, лежащей на этой на этой прямой, и координаты направляющего вектора, то есть вектора, коллинеарного прямой.

Прямая является линией пересечения двух плоскостей, поэтому ее направляющий вектор А параллелен каждой из этих плоскостей и соответственно перпендикулярен нормалям П1 и П2 к данным плоскостям. В таком случае он коллинеарен векторному произведению [N1, N2].

Будем искать точку, лежащую на данной прямой, у которой одна из координат принимает выбранное нами значение; тогда остальные две координаты можно определить единственным образом из системы уравнений, задающей пересекающиеся плоскости. Выберем для удобства вычислений Z0 = 0, тогда для точки М=<Х0; У0; 0>

Теперь составим канонические уравнения данной прямой:

Ответ:

Составить уравнение плоскости, проходящей через прямую L:

Точка А= принадлежит плоскости, соответственно вектор параллелен плоскости. Кроме того, поскольку данная прямая лежит в плоскости, ее направляющий вектор A = (2: 1: -1) параллелен плоскости. Следовательно, нормаль к плоскости коллинеарна векторному произведению этих векторов.

Поскольку прямая лежит в плоскости, ее направляющий вектор A = (2: 1: -1) параллелен плоскости. При T = 0 из уравнений прямой получаем:

Координаты точки А, принадлежащей прямой и соОтВетственно плоскости.

Тогда вектор АМ = (5; -8; 2) параллелен Плоскости. Следовательно, нормаль

П к плоскости коллинеарна векторному произведению [A, AM] = (-6; -9; — 21).

Выберем N = (2; 3; 7) и составим уравнение плоскости, проходящей через

Найти кратчайшее расстояние между прямыми

Координаты направляющих векторов данных прямых A1 = и

A2 = не пропорциональны, следовательно, А1 и А2 не коллинеарны, поэтому прямые либо пересекаются, либо скрещиваются.

Составьте уравнение плоскости A, проходящей через прямую L1 параллельно вектору А2. Если L1 и L2 пересекаются, то прямая L2 будет лежать в этой плоскости; если же L1 и L2 скрещиваются, то L2 параллельна плоскости A, и тогда расстояние между L1 и L2 (длина общего перпендикуляра) будет равно расстоянию от любой точки прямой L2 до плоскости A.

Координаты направляющих векторов данных прямых A1 = и

A2 = не пропорциональны, следовательно, А1 и А2 не коллинеарны, поэтому прямые либо пересекаются, либо скрещиваются.

Составим уравнение плоскости A, проходящей через прямую L1 параллельно вектору А2. Если L1 и L2 пересекаются, то прямая L2 будет лежать в этой плоскости (рис.9); если же L1 и L2 скрещиваются, то L2 параллельна плоскости A, и тогда расстояние между L1 и L2 (длина общего перпендикуляра) будет равно расстоянию от любой точки прямой L2 до плоскости A (рис.10).

[A1, A2] = (10; -14; 1) = N, точка А= лежит на прямой L1, следова-тельно, она лежит и в плоскости A. Тогда уравнение плоскости A имеет вид:

Точка В= принадлежит прямой L2. Проверим, лежит ли эта точка в плоскости A:

Тогда искомой величиной будет расстояние от В до A. Его можно найти, составив нормальное уравнение плоскости A:

Ответ: .

Найти точку, симметричную точке А(5; -10; 4) относительно плоскости

Искомая точка В лежит на прямой, проходящей через точку А перпендикулярно плоскости A так, что ОА = ОВ, где точка О – точка пересечения A с прямой АВ.

Искомая точка В лежит на прямой, проходящей через точку А перпендикулярно плоскости A так, что ОА = ОВ, где точка О – точка пересечения A с прямой АВ. Составим уравнения прямой АВ. Эта прямая перпендикулярна A, поэтому ее направляющим вектором можно считать нормаль к плоскости A: A = N = (1; -3; 1).

Параметрические уравнения прямой АВ имеют вид:

Точка О принадлежит и прямой АВ, и плоскости A, поэтому ее координаты должны удовлетворять и уравнениям прямой, и уравнению плоскости. Подставим в уравнение плоскости A параметрические выражения для X, Y, Z из уравнений прямой АВ:

T + 5 – 3(-3T – 10) + T + 4 – 6 = 0; 11T + 33 = 0; T = -3.

Итак, координаты точки О:

Поскольку точка О – середина отрезка АВ, то

📹 Видео

Видеоурок "Уравнение плоскости в отрезках"Скачать

2. Уравнение плоскости примеры решения задач #1Скачать

Уравнение плоскости. Практика. Урок 5. Геометрия 11 классСкачать

4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Уравнение плоскости через 2 точки параллельно векторуСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

17. Показать что прямые пересекаются и составить уравнение плоскости в которой они расположеныСкачать

3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Лекция 25. Виды уравнений плоскости в пространстве.Скачать

3. Уравнение плоскостиСкачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать