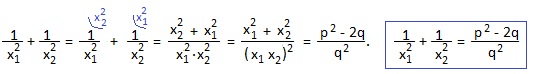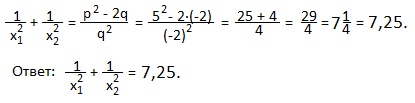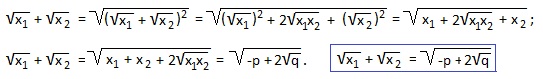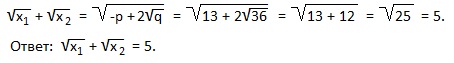Один из корней квадратного уравнения x2 px 36 0 равен 9

Если необходимо найти 2 корня, то D > 0

Нам не уточнили, какой именно корень -9 — больший или меньший, поэтому проверяем оба условия

— не соответствует ОДЗ

При обоих условиях ответ один и тот же, за счёт того, что на 4 шаге мы возводим в квадрат одно и то же выражение

Но во втором уравнении при p = 7 равенство не получится

Следовательно, исходное уравнение будет иметь вид

А чтобы получить второй корень, в формуле уже будем складывать

-p и корень дискриминанта, т.к. минус даёт уже известный нам меньший корень -9

Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

В уравнении x2 + px — 36 = 0 один из корней равен — 12 найдите другой корень и p?

Алгебра | 5 — 9 классы

В уравнении x2 + px — 36 = 0 один из корней равен — 12 найдите другой корень и p.

По обратной теореме Виета : — 12 + x2 = — p — 12×2 = — 36

x2 = 3 — 12 + 3 = — p

Ответ : х2 = 3 ; p = 9.

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Один из корней уравнения 3х ^ 2 — bx + 36 = 0 равен — 3?

Один из корней уравнения 3х ^ 2 — bx + 36 = 0 равен — 3.

Найдите второй корень.

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Один из корней уравнения x2 + 11 х + а = 0 равен 3?

Один из корней уравнения x2 + 11 х + а = 0 равен 3.

Найдите другой корень.

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

В уравнении x² — kx + 6 = 0 один из корней равен 1?

В уравнении x² — kx + 6 = 0 один из корней равен 1.

Найдите коэффицент k и второй корень уравнения.

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

В уравнении x2 — px + 8 = 0 один из корней равен –1?

В уравнении x2 — px + 8 = 0 один из корней равен –1.

Найдите коэффициент p и второй корень уравнения.

Видео:Уравнение x^2+px+q=0 имеет корни -6; 4. Найдите q. | ОГЭ 2017 | ЗАДАНИЕ 4 | ШКОЛА ПИФАГОРАСкачать

В уравнении 3x ^ 2 — 19x — c = 0 один из корней равен 7?

В уравнении 3x ^ 2 — 19x — c = 0 один из корней равен 7.

Найдите c и второй корень уравнения.

Видео:Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать

Один из корней квадратного уравнения x² + 17x — 38 = 0 равен 2 ?

Один из корней квадратного уравнения x² + 17x — 38 = 0 равен 2 .

Найдите второй корень уравнения .

Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

В уравнении x ^ 2 + px + 5 = 0 один из корней равен 1 ?

В уравнении x ^ 2 + px + 5 = 0 один из корней равен 1 .

Найдите p и другой корень.

Видео:Математика Один из корней уравнения 3x^2 +5x +2m =0 равен -1. Найдите второй корень.Скачать

Один из корней уравнения х2 + ах + 12 = 0 равен 9?

Один из корней уравнения х2 + ах + 12 = 0 равен 9.

Найдите другой корень и коэффициент а.

Видео:Алгебра 8 класс (Урок№19 - Уравнение х² = а.)Скачать

Один из корней уравнения x ^ 2 + bx + 32 = 0 равен 4?

Один из корней уравнения x ^ 2 + bx + 32 = 0 равен 4.

Найдите коэффициент в и второй корень уравнения.

Видео:Найти сумму корней квадратного уравнения, если дискриминант равен нулюСкачать

Один из корней квадратного уравнения x ^ 2 + cx + 15 = 0 равен 5?

Один из корней квадратного уравнения x ^ 2 + cx + 15 = 0 равен 5.

Найдите c и другой корень уравнения.

Вы зашли на страницу вопроса В уравнении x2 + px — 36 = 0 один из корней равен — 12 найдите другой корень и p?, который относится к категории Алгебра. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

10 монет по 20 копеек. Это если у них ещё при этом остануться деньги. А если не остануться, то 5 монет по 20 копеек.

Можно было решать еще так : приравняем каждый множитель к нулю х — 6 = 0 х = 6 3 — 2х = 0 — 2х = — 3 х = 3 / 2 х = 6 ; 3 / 2 .

(x — 6)(3 — 2х) = 0 x * 3 + x * ( — 2x) — 6 * 3 — 6 * ( — 2x) = 0 3x — 2x² — 18 + 12x = 0 15x — 2x² — 18 = 0 D = 15² — 4 * ( — 2) * ( — 18) 255 — 4 * ( — 2) * ( — 18) 225 — 4 * 36 225 — 144 = 81 81 = 9² Ответом к вашему уравнению будут : x1 = 6 , x2..

5км / час 25 — 20 = 5 30 — 25 = 5 Ответ : 5км / чам.

√9√в ^ 16 √3 ^ 2 в ^ 8 3в ^ 8 во второй строке в ^ 8 не под корнем.

Постарался как можно подробно если что, где чёркнуто, это сокращения.

Первое задание : корни уравнения получаем тривиально 0 и 2 график — парабола, середину отражаем вдоль оси ОХ Второе задание : только корни 0 и 4, график тоже в приложении Третье задание : видно, что это уравнение параболы, корень очевидно равен Х = 0..

(a + 1)x² + 2ax + a + 3 = 01) D = (2a)² — 4(a + 1)(a + 3) = — 16a — 12чтобы кв. Ур — е имело 2 корня, нужно, чтобы D>0⇒ — 16a — 12>0⇒a0 ; x₂>0, значит, 00по т. Виета имеем : 00<( — ∞ ; — 3)∪( — 1 ..

(a + 1)x² + 2ax + a + 3 = 0 1) D = (2a)² — 4(a + 1)(a + 3) = — 16a — 12 чтобы кв. Ур — е имело 2 корня, нужно, чтобы D>0⇒ — 16a — 12>0⇒a0 ; x₂>0, значит, 0 0 по т. Виета имеем : 0 0 <( — ∞ ; — 3)∪..

Начала примеров исходных не переписываю , сразу решение a(x + y) + 7(x + y) = (a + 7)(x + y) y²(y — 1) + 1(y — 1) = (y² + 1)(y — 1) Комментарий от меня. Здесь всё решается почти через формулу квадрата разности a² — b² (a + b)(a — b), главное её ув..

Видео:Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать

8.2.4. Применение теоремы Виета

Часто требуется найти сумму квадратов (x₁ 2 +x₂ 2 ) или сумму кубов (x₁ 3 +x₂ 3 ) корней квадратного уравнения, реже — сумму обратных значений квадратов корней или сумму арифметических квадратных корней из корней квадратного уравнения:

Помочь в этом может теорема Виета:

Сумма корней приведенного квадратного уравнения x 2 +px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

Выразим через p и q:

1) сумму квадратов корней уравнения x 2 +px+q=0;

2) сумму кубов корней уравнения x 2 +px+q=0.

Решение.

1) Выражение x₁ 2 +x₂ 2 получится, если взвести в квадрат обе части равенства x₁+x₂=-p;

(x₁+x₂) 2 =(-p) 2 ; раскрываем скобки: x₁ 2 +2x₁x₂+ x₂ 2 =p 2 ; выражаем искомую сумму: x₁ 2 +x₂ 2 =p 2 -2x₁x₂=p 2 -2q. Мы получили полезное равенство: x₁ 2 +x₂ 2 =p 2 -2q.

2) Выражение x₁ 3 +x₂ 3 представим по формуле суммы кубов в виде:

Еще одно полезное равенство: x₁ 3 +x₂ 3 =-p·(p 2 -3q).

Примеры.

3) x 2 -3x-4=0. Не решая уравнение, вычислите значение выражения x₁ 2 +x₂ 2 .

Решение.

По теореме Виета сумма корней этого приведенного квадратного уравнения

x₁+x₂=-p=3, а произведение x₁∙x₂=q=-4. Применим полученное нами (в примере 1) равенство:

x₁ 2 +x₂ 2 =p 2 -2q. У нас -p=x₁+x₂=3 → p 2 =3 2 =9; q=x₁x₂=-4. Тогда x₁ 2 +x₂ 2 =9-2·(-4)=9+8=17.

4) x 2 -2x-4=0. Вычислить: x₁ 3 +x₂ 3 .

Решение.

По теореме Виета сумма корней этого приведенного квадратного уравнения x₁+x₂=-p=2, а произведение x₁∙x₂=q=-4. Применим полученное нами (в примере 2) равенство: x₁ 3 +x₂ 3 =-p·(p 2 -3q)=2·(2 2 -3·(-4))=2·(4+12)=2·16=32.

Ответ: x₁ 3 +x₂ 3 =32.

Вопрос: а если нам дано не приведенное квадратное уравнение? Ответ: его всегда можно «привести», разделив почленно на первый коэффициент.

5) 2x 2 -5x-7=0. Не решая, вычислить: x₁ 2 +x₂ 2 .

Решение. Нам дано полное квадратное уравнение. Разделим обе части равенства на 2 (первый коэффициент) и получим приведенное квадратное уравнение: x 2 -2,5x-3,5=0.

По теореме Виета сумма корней равна 2,5; произведение корней равно -3,5.

Решаем так же, как пример 3), используя равенство: x₁ 2 +x₂ 2 =p 2 -2q.

x₁ 2 +x₂ 2 =p 2 -2q=2,5 2 -2∙(-3,5)=6,25+7=13,25.

Ответ: x₁ 2 +x₂ 2 =13,25.

6) x 2 -5x-2=0. Найти:

Преобразуем это равенство и, заменив по теореме Виета сумму корней через -p, а произведение корней через q, получим еще одну полезную формулу. При выводе формулы использовали равенство 1): x₁ 2 +x₂ 2 =p 2 -2q.

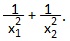
В нашем примере x₁+x₂=-p=5; x₁∙x₂=q=-2. Подставляем эти значения в полученную формулу:

7) x 2 -13x+36=0. Найти:

Преобразуем эту сумму и получим формулу, по которой можно будет находить сумму арифметических квадратных корней из корней квадратного уравнения.

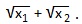
У нас x₁+x₂=-p=13; x₁∙x₂=q=36. Подставляем эти значения в выведенную формулу:

Совет: всегда проверяйте возможность нахождения корней квадратного уравнения по подходящему способу, ведь 4 рассмотренные полезные формулы позволяют быстро выполнить задание, прежде всего, в тех случаях, когда дискриминант — «неудобное» число. Во всех простых случаях находите корни и оперируйте ими. Например, в последнем примере подберем корни по теореме Виета: сумма корней должна быть равна 13, а произведение корней 36. Что это за числа? Конечно, 4 и 9. А теперь считайте сумму квадратных корней из этих чисел: 2+3=5. Вот так то!

📹 Видео

Квадратное уравнение. Как решить? | Математика ОГЭ 2023 | УмскулСкачать

СЛОЖИТЕ ДВА КОРНЯСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

8 класс, 25 урок, Формула корней квадратного уравненияСкачать

Свойства квадратного корня. Уравнение х2=а, 8 классСкачать

РАЗБИРАЕМ ДИСКРИМИНАНТ ЧАСТЬ I #shorts #математика #егэ #огэ #дискриминантСкачать

Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать

Формула корней квадратного уравнения – 8 класс алгебраСкачать