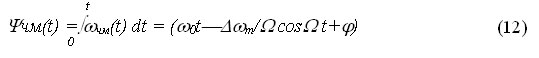Общие сведения о модуляции
Модуляция — это процесс преобразования одного или нескольких информационных параметров несущего сигнала в соответствии с мгновенными значениями информационного сигнала.
В результате модуляции сигналы переносятся в область более высоких частот.
Использование модуляции позволяет:
- согласовать параметры сигнала с параметрами линии;
- повысить помехоустойчивость сигналов;
- увеличить дальность передачи сигналов;
- организовать многоканальные системы передачи (МСП с ЧРК).
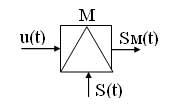
Модуляция осуществляется в устройствах модуляторах. Условное графическое обозначение модулятора имеет вид:
Рисунок 1 — Условное графическое обозначение модулятора
При модуляции на вход модулятора подаются сигналы:
u(t) — модулирующий, данный сигнал является информационным и низкочастотным (его частоту обозначают W или F);
S(t) — модулируемый (несущий), данный сигнал является неинформационным и высокочастотным (его частота обозначается w0 или f0);
Sм(t) — модулированный сигнал, данный сигнал является информационным и высокочастотным.
В качестве несущего сигнала может использоваться:
- гармоническое колебание, при этом модуляция называется аналоговой или непрерывной;
- периодическая последовательность импульсов, при этом модуляция называется импульсной;
- постоянный ток, при этом модуляция называется шумоподобной.
Так как в процессе модуляции изменяются информационные параметры несущего колебания, то название вида модуляции зависит от изменяемого параметра этого колебания.
1. Виды аналоговой модуляции:
- амплитудная модуляция (АМ), происходит изменение амплитуды несущего колебания;
- частотная модуляция (ЧМ), происходит изменение частоты несущего колебания;
- фазовая модуляция (ФМ), происходит изменение фазы несущего колебания.
2. Виды импульсной модуляции:
- амплитудно-импульсная модуляция (АИМ), происходит изменение амплитуды импульсов несущего сигнала;
- частотно-импульсная модуляция (ЧИМ), происходит изменение частоты следования импульсов несущего сигнала;
- Фазо-импульсная модуляция (ФИМ), происходит изменение фазы импульсов несущего сигнала;
- Широтно-импульсная модуляция (ШИМ), происходит изменение длительности импульсов несущего сигнала.
Амплитудная модуляция
Амплитудная модуляция — процесс изменения амплитуды несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.
Рассмотрим математическую модель амплитудно-модулированного (АМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала
на несущее колебание
происходит изменение амплитуды несущего сигнала по закону:
где аам — коэффициент пропорциональности амплитудной модуляции.
Подставив (3) в математическую модель (2) получим:
Вынесем Um за скобки:
Отношение аам Umu/Um = mам называется коэффициентом амплитудной модуляции. Данный коэффициент не должен превышать единицу, т. к. в этом случае появляются искажения огибающей модулированного сигнала называемые перемодуляцией. С учетом mам математическая модель АМ сигнала при гармоническом модулирующем сигнале будет иметь вид:
Если модулирующий сигнал u(t) является негармоническим, то математическая модель АМ сигнала в этом случае будет иметь вид:
Рассмотрим спектр АМ сигнала для гармонического модулирующего сигнала. Для этого раскроем скобки математической модели модулированного сигнала, т. е. представим его в виде суммы гармонических составляющих.
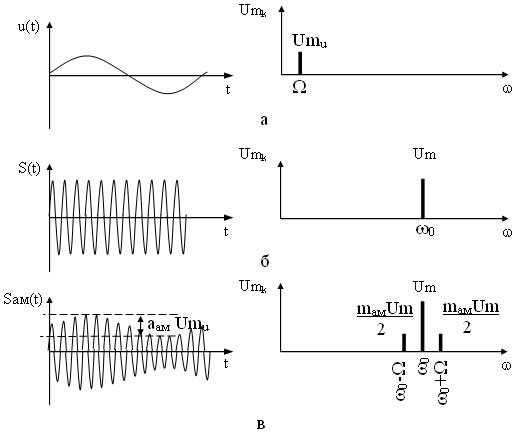
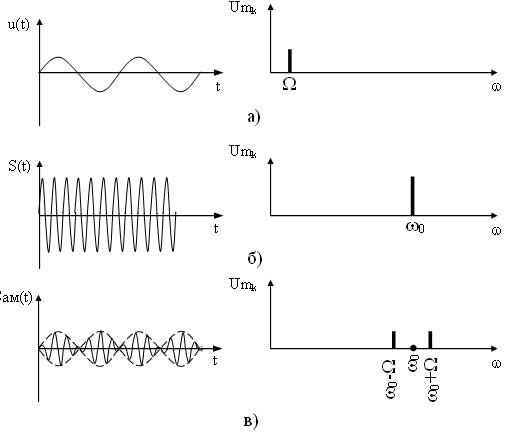
Как видно из выражения в спектре АМ сигнала присутствует три составляющих: составляющая несущего сигнала и две составляющих на комбинационных частотах. Причем составляющая на частоте ?0—? называется нижней боковой составляющей, а на частоте ?0 + ? — верхней боковой составляющей. Спектральные и временные диаграммы модулирующего, несущего и амплитудно-модулированного сигналов имеют вид (рисунок 2).
Рисунок 2 — Временные и спектральные диаграммы модулирующего (а), несущего (б) и ампдтудно-модулированного (в) сигналов
Ширина спектра для данного сигнала будет определятся
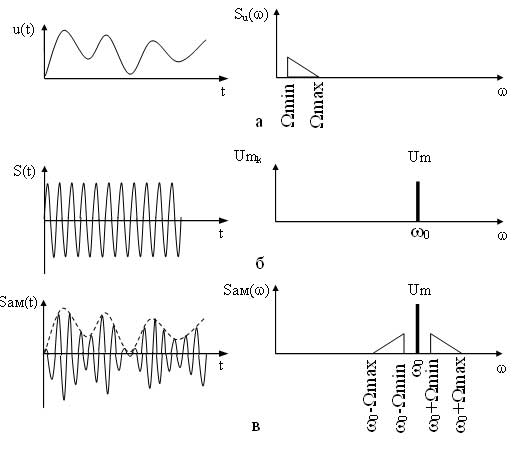
Если же модулирующий сигнал является случайным, то в этом случае в спектре составляющие модулирующего сигнала обозначают символически треугольниками (рисунок 3).
Рисунок 3 — Временные и спектральные диаграммы сигналов при случайном модулирующем сигнале
Ширина спектра для данного сигнала будет определятся
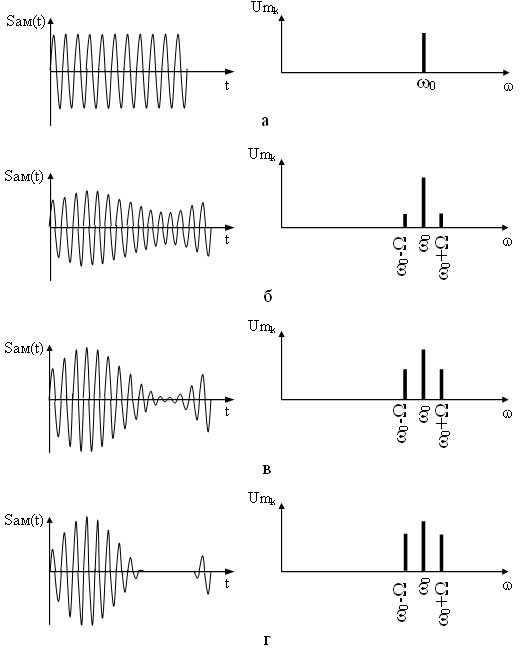
На рисунке 4 приведены временные и спектральные диаграммы АМ сигналов при различных индексах mам. Как видно при mам=0 модуляция отсутствует, сигнал представляет собой немодулированную несущую, соответственно и спектр этого сигнала имеет только составляющую несущего сигнала (рисунок 4,
Рисунок 4 — Временные и спектральные диаграммы АМ сигналов при различных mам: а) при mам=0, б) при mам=0,5, в) при mам=1, г) при mам>1
а), при индексе модуляции mам=1 происходит глубокая модуляция, в спектре АМ сигнала амплитуды боковых составляющих равны половине амплитуды составляющей несущего сигнала (рисунок 4в), данный вариант является оптимальным, т. к. энергия в большей степени приходится на информационные составляющие. На практике добиться коэффициента равного едините тяжело, поэтому добиваются соотношения 0 1 происходит перемодуляция, что, как отмечалось выше, приводит к искажению огибающей АМ сигнала, в спектре такого сигнала амплитуды боковых составляющих превышают половину амплитуды составляющей несущего сигнала (рисунок 4г).
Основными достоинствами амплитудной модуляции являются:
- узкая ширина спектра АМ сигнала;
- простота получения модулированных сигналов.
Недостатками этой модуляции являются:
- низкая помехоустойчивость (т. к. при воздействии помехи на сигнал искажается его форма — огибающая, которая и содержит передаваемое сообщение);
- неэффективное использование мощности передатчика (т. к. наибольшая часть энергии модулированного сигнала содержится в составляющей несущего сигнала до 64%, а на информационные боковые полосы приходится по 18%).
Амплитудная модуляция нашла широкое применение:
- в системах телевизионного вещания (для передачи телевизионных сигналов);
- в системах звукового радиовещания и радиосвязи на длинных и средних волнах;
- в системе трехпрограммного проводного вещания.
Балансная и однополосная модуляция
Как отмечалось выше, одним из недостатков амплитудной модуляции является наличие составляющей несущего сигнала в спектре модулированного сигнала. Для устранения этого недостатка применяют балансную модуляцию. При балансной модуляциипроисходит формирование модулированного сигнала без составляющей несущего сигнала. В основном это осуществляется путем использования специальных модуляторов: балансного или кольцевого. Временная диаграмма и спектр балансно-модулированного (БМ) сигнала представлен на рисунке 5.
Рисунок 5 — Временные и спектральные диаграммы модулирующего (а), несущего (б) и балансно-модулированного (в) сигналов
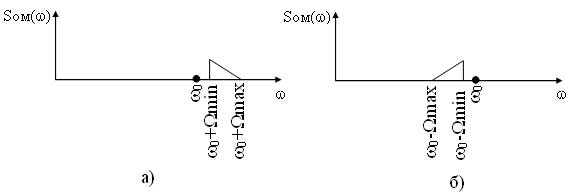
Также особенностью модулированного сигнала является наличие в спектре двух боковых полос несущих одинаковую информацию. Подавление одной из полос позволяет уменьшить спектр модулированного сигнала и, соответственно, увеличить число каналов в линии связи. Модуляция при которой формируется модулированный сигнал с одной боковой полосой (верхней или нижней) называется однополосной. Формирование однополосно-модулированного (ОМ) сигнала осуществляется из БМ сигнала специальными методами, которые рассматриваются ниже. Спектры ОМ сигнала представлены на рисунке 6.
Рисунок 6 — Спектральные диаграммы однополосно-модулированных сигналов: а) с верхней боковой полосой (ВБП), б) с нижней боковой полосой (НБП)
Частотная модуляция
Частотная модуляция — процесс изменения частоты несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.
Рассмотрим математическую модель частотно-модулированного (ЧМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала
на несущее колебание
происходит изменение частоты несущего сигнала по закону:
где ачм — коэффициент пропорциональности частотной модуляции.
Поскольку значение sin ? t может изменятся в диапазоне от -1 до 1, то наибольшее отклонение частоты ЧМ сигнала от частоты несущего сигнала составляет
Величина Dwm называется девиацией частоты. Следовательно, девиация частоты показывает наибольшее отклонение частоты модулированного сигнала от частоты несущего сигнала.
Значение ? чм(t) непосредственно подставить в S(t) нельзя, т. к. аргумент синуса ? t+j является мгновенной фазой сигнала ?(t) которая связана с частотой выражением
Отсюда следует что, чтобы определить ?чм(t) необходимо проинтегрировать ?чм(t)
Причем в выражении (12) ? является начальной фазой несущего сигнала.
называется индексом частотной модуляции.
Учитывая (12) и (13) математическая модель ЧМ сигнала при гармоническом модулирующем сигнале будет иметь вид:
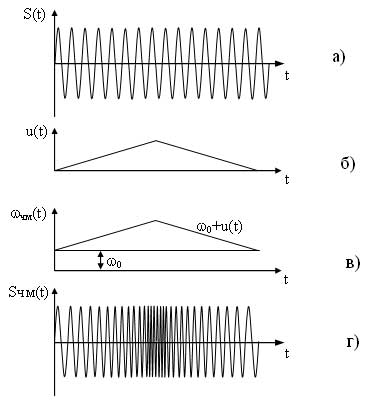
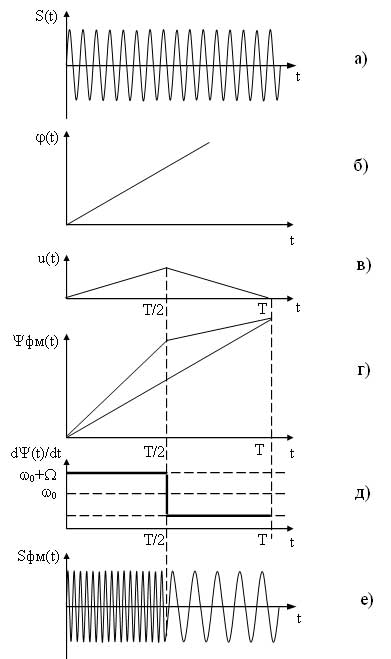
Временные диаграммы, поясняющие процесс формирования частотно-модулированного сигнала приведены на рисунке 7. На первых диаграммах а) и б) представлены соответственно несущий и модулирующий сигналы, на рисунке в) представлена диаграмма показывающая закон изменения частоты ЧМ сигнала. На диаграмме г) представлен частогтно-модулированный сигнал соответствующий заданному модулирующему сигналу, как видно из диаграммы любое изменение амплитуды модулирующего сигнала вызывает пропорциональное изменение частоты несущего сигнала.
Рисунок 7 — Формирование ЧМ сигнала
Для построения спектра ЧМ сигнала необходимо разложить его математическую модель на гармонические составляющие. В результате разложения получим
где Jk(Mчм) — коэффициенты пропорциональности.
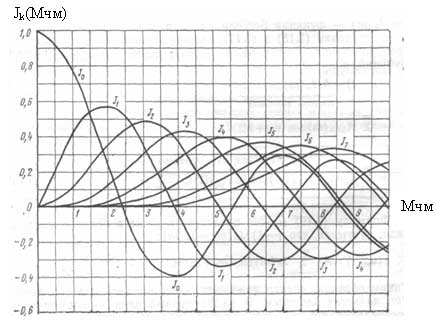
Jk(Mчм) определяются по функциям Бесселя и зависят от индекса частотной модуляции. На рисунке 8 представлен график содержащий восемь функций Бесселя. Для определения амплитуд составляющих спектра ЧМ сигнала необходимо определить значение функций Бесселя для заданного индекса. Причем как
Рисунок 8 — Функции Бесселя
видно из рисунка различные функции имеют начало в различных значениях Мчм, а следовательно, количество составляющих в спектре будет определятся Мчм (с увеличивается индекса увеличивается и количество составляющих спектра). Например необходимо определить коэффициенты Jk(Мчм) при Мчм=2. По графику видно, что при заданном индексе можно определить коэффициенты для пяти функций (J0, J1, J2, J3, J4) Их значение при заданном индексе будет равно: J0=0,21; J1=0,58; J2=0,36; J3=0,12; J4=0,02. Все остальные функции начинаются после значения Мчм=2 и равны, соответственно, нулю. Для приведенного примера количество составляющих в спектре ЧМ сигнала будет равно 9: одна составляющая несущего сигнала (Um J0) и по четыре составляющих в каждой боковой полосе (Um J1; Um J2; Um J3; Um J4).
Еще одной важной особенностью спектра ЧМ сигнала является то, что можно добиться отсутствия составляющей несущего сигнала или сделать ее амплитуду значительно меньше амплитуд информационных составляющих без дополнительных технических усложнений модулятора. Для этого необходимо подобрать такой индекс модуляции Мчм, при котором J0(Мчм) будет равно нулю (в месте пересечения функции J0 с осью Мчм), например Мчм=2,4.
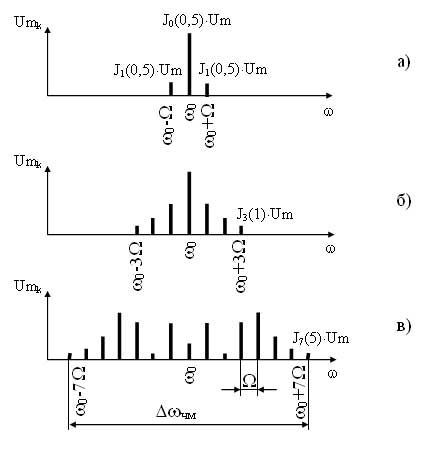
Поскольку увеличение составляющих приводит к увеличению ширины спектра ЧМ сигнала, то значит, ширина спектра зависит от Мчм (рисунок 9). Как видно из рисунка, при Мчм ?0,5 ширина спектра ЧМ сигнала соответствует ширине спектра АМ сигнала и в этом случае частотная модуляция является узкополосной, при увеличении Мчм ширина спектра увеличивается, и модуляция в этом случае является широкополосной. Для ЧМ сигнала ширина спектра определяется
Достоинством частотной модуляции являются:
- высокая помехоустойчивость;
- более эффективное использование мощности передатчика;
- сравнительная простота получения модулированных сигналов.
Основным недостатком данной модуляции является большая ширина спектра модулированного сигнала.
Частотная модуляция используется:
- в системах телевизионного вещания (для передачи сигналов звукового сопровождения);
- системах спутникового теле- и радиовещания;
- системах высококачественного стереофонического вещания (FM диапазон);
- радиорелейных линиях (РРЛ);
- сотовой телефонной связи.
Рисунок 9 — Спектры ЧМ сигнала при гармоническом модулирующем сигнале и при различных индексах Мчм: а) при Мчм=0,5, б) при Мчм=1, в) при Мчм=5
Фазовая модуляция
Фазовая модуляция — процесс изменения фазы несущего сигнала в соответствии с мгновенными значениями модулирующего сигнала.
Рассмотрим математическую модель фазо-модулированного (ФМ) сигнала при гармоническом модулирующем сигнале. При воздействии модулирующего сигнала
на несущее колебание
происходит изменение мгновенной фазы несущего сигнала по закону:
где афм — коэффициент пропорциональности частотной модуляции.
Подставляя ?фм(t) в S(t) получаем математическую модель ФМ сигнала при гармоническом модулирующем сигнале:
Произведение афм Umu=Djm называется индексом фазовой модуляции или девиацией фазы.
Поскольку изменение фазы вызывает изменение частоты, то используя (11) определяем закон изменения частоты ФМ сигнала:
Произведение афмUmu?=??m является девиацией частоты фазовой модуляции. Сравнивая девиацию частоты при частотной и фазовой модуляциях можно сделать вывод, что и при ЧМ и при ФМ девиация частоты зависит от коэффициента пропорциональности и амплитуды модулирующего сигнала, но при ФМ девиация частоты также зависит и от частоты модулирующего сигнала.
Временные диаграммы поясняющие процесс формирования ФМ сигнала приведены на рисунке 10.
При разложении математической модели ФМ сигнала на гармонические составляющие получится такой же ряд, как и при частотной модуляции (15), с той лишь разницей, что коэффициенты Jk будут зависеть от индекса фазовой модуляции ? ?m (Jk(? ?m)). Определятся эти коэффициенты будут аналогично, как и при ЧМ, т. е. по функциям Бесселя, с той лишь разницей, что по оси абсцисс необходимо заменить Мчм на ? ?m. Поскольку спектр ФМ сигнала строится аналогично спектру ЧМ сигнала, то для него характерны те же выводы что и для ЧМ сигнала (пункт 1.4).
Рисунок 10 — Формирование ФМ сигнала
Ширина спектра ФМ сигнала определяется выражением:
Достоинствами фазовой модуляции являются:
- высокая помехоустойчивость;
- более эффективное использование мощности передатчика.
- недостатками фазовой модуляции являются:
- большая ширина спектра;
- сравнительная трудность получения модулированных сигналов и их детектирование
Дискретная двоичная модуляция (манипуляция гармонической несущей)
Дискретная двоичная модуляция (манипуляция) — частный случай аналоговой модуляции, при которой в качестве несущего сигнала используется гармоническая несущая, а в качестве модулирующего сигнала используется дискретный, двоичный сигнал.
Различают четыре вида манипуляции:
- амплитудную манипуляцию (АМн или АМТ);
- частотную манипуляцию (ЧМн или ЧМТ);
- фазовую манипуляцию (ФМн или ФМТ);
- относительно-фазовую манипуляцию (ОФМн или ОФМ).
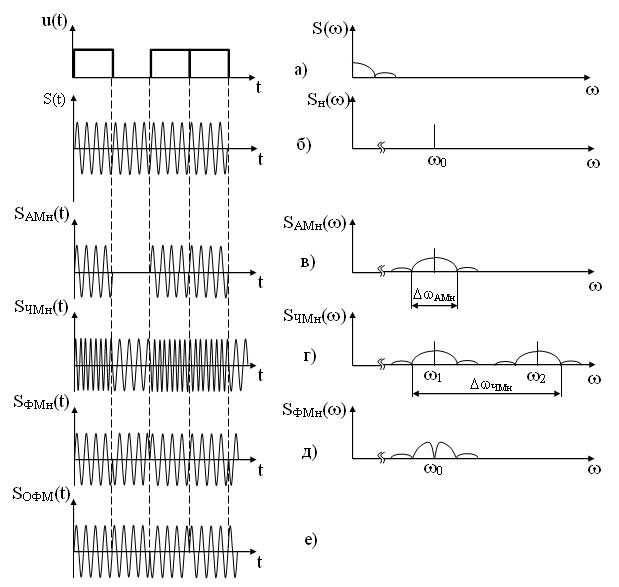
Временные и спектральные диаграммы модулированных сигналов при различных видах манипуляции представлены на рисунке 11.
При амплитудной манипуляции, также как и при любом другом модулирующем сигнале огибающая SАМн(t) повторяет форму модулирующего сигнала (рисунок 11, в).
При частотной манипуляции используются две частоты ?1 и ?2. При наличии импульса в модулирующем сигнале (посылке) используется более высокая частота ?2, при отсутствии импульса (активной паузе) используется более низкая частота w1 соответствующая немодулированной несущей (рисунок 11, г)). Спектр частотно-манипулированного сигнала SЧМн(t) имеет две полосы возле частот ?1 и ?2.
При фазовой манипуляции фаза несущего сигнала изменяется на 180° в момент изменения амплитуды модулирующего сигнала. Если следует серия из нескольких импульсов, то фаза несущего сигнала на этом интервале не изменяется (рисунок 11, д).
Рисунок 11 — Временные и спектральные диаграммы модулированных сигналов различных видов дискретной двоичной модуляции
При относительно-фазовой манипуляции фаза несущего сигнала изменяется на 180° лишь в момент подачи импульса, т. е. при переходе от активной паузы к посылке (0?1) или от посылке к посылке (1?1). При уменьшении амплитуды модулирующего сигнала фаза несущего сигнала не изменяется (рисунок 11, е). Спектры сигналов при ФМн и ОФМн имеют одинаковый вид (рисунок 9, е).
Сравнивая спектры всех модулированных сигналов можно отметить, что наибольшую ширину имеет спектр ЧМн сигнала, наименьшую — АМн, ФМн, ОФМн, но в спектрах ФМн и ОФМн сигналов отсутствует составляющая несущего сигнала.
В виду большей помехоустойчивости наибольшее распространение получили частотная, фазовая и относительно-фазовая манипуляции. Различные их виды используются в телеграфии, при передаче данных, в системах подвижной радиосвязи (телефонной, транкинговой, пейджинговой).
Импульсная модуляция
Импульсная модуляция — это модуляция, при которой в качестве несущего сигнала используется периодическая последовательность импульсов, а в качестве модулирующего может использоваться аналоговый или дискретный сигнал.
Поскольку периодическая последовательность характеризуется четырьмя информационными параметрами (амплитудой, частотой, фазой и длительностью импульса), то различают четыре основных вида импульсной модуляции:
- амплитудно-импульсная модуляция (АИМ); происходит изменение амплитуды импульсов несущего сигнала;
- частотно-импульсная модуляция (ЧИМ), происходит изменение частоты следования импульсов несущего сигнала;
- фазо-импульсная модуляция (ФИМ), происходит изменение фазы импульсов несущего сигнала;
- широтно-импульсная модуляция (ШИМ), происходит изменение длительности импульсов несущего сигнала.
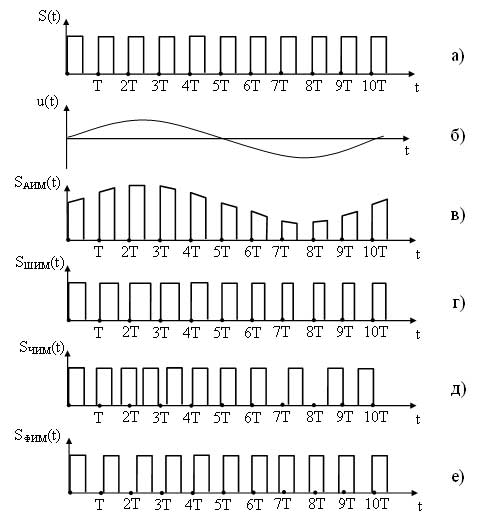
Временные диаграммы импульсно-модулированных сигналов представлены на рисунке 12.
При АИМ происходит изменение амплитуды несущего сигнала S(t) в соответствии с мгновенными значениями модулирующего сигнала u(t), т. е. огибающая импульсов повторяет форму модулирующего сигнала (рисунок 12, в).
При ШИМ происходит изменение длительности импульсов S(t) в соответствии с мгновенными значениями u(t) (рисунок 12, г).
Рисунок 12 — Временные диаграммы сигналов при импульсной модуляции
При ЧИМ происходит изменение периода, а соответственно и частоты, несущего сигнала S(t) в соответствии с мгновенными значениями u(t) (рисунок 12, д).
При ФИМ происходит смещение импульсов несущего сигнала относительно их тактового (временного) положения в немодулированной несущей (тактовые моменты обозначены на диаграммах точками Т, 2Т, 3Т и т. д.). ФИМ сигнал представлен на рисунке 12, е.
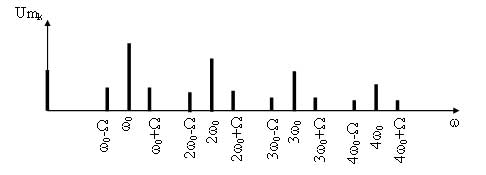
Поскольку при импульсной модуляции переносчиком сообщения является периодическая последовательность импульсов, то спектр импульсно-модулированных сигналов является дискретным и содержит множество спектральных составляющих. Этот спектр представляет собой спектр периодической последовательности импульсов в котором возле каждой гармонической составляющей несущего сигнала находятся составляющие модулирующего сигнала (рисунок 13). Структура боковых полос возле каждой составляющей несущего сигнала зависит от вида модуляции.
Рисунок 13 — Спектр импульсно-модулированного сигнала
Также важной особенностью спектра импульсно-модулированных сигналов является то, что ширина спектра модулированного сигнала, кроме ШИМ, не зависит от модулирующего сигнала. Она полностью определяется длительностью импульса несущего сигнала. Поскольку при ШИМ длительность импульса изменяется и зависит от модулирующего сигнала, то при этом виде модуляции и ширина спектра также зависти от модулирующего сигнала.
Частоту следования импульсов несущего сигнала может быть определена по теореме В. А. Котельникова как f0 =2Fmax. При этом Fmax это верхняя частота спектра модулирующего сигнала.
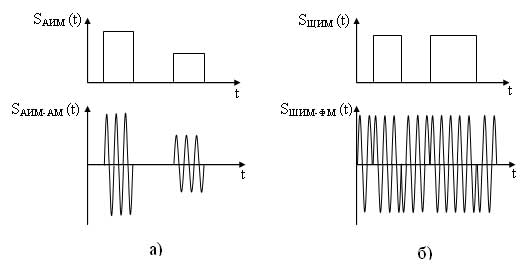
Передача импульсно модулированных сигналов по высокочастотным линиям связи невозможна, т. к. спектр этих сигналов содержит низкочастотные составляющий. Поэтому для передачи осуществляют повторную модуляцию. Это модуляция, при которой в качестве модулирующего сигнала используют импульсно-модулированный сигнал, а в качестве несущего гармоническое колебание. При повторной модуляции спектр импульсно-модулированного сигнала переносится в область несущей частоты. Для повторной модуляции может использоваться любой из видов аналоговой модуляции: АМ, ЧС, ФМ. Полученная модуляция обозначается двумя аббревиатурами: первая указывает на вид импульсной модуляции а вторая — на вид аналоговой модуляции, например АИМ-АМ (рисунок 14, а) или ШИМ-ФМ (рисунок 14, б) и т. д.
Рисунок 14 — Временные диаграммы сигналов при импульсной повторной модуляции
Видео:Модуляция. Базовые понятияСкачать

Фазовая модуляция: теория, временная и частотная области
Фазовая модуляция (ФМ, англ. PM) похожа на частотную модуляцию и является важной технологией в цифровых системах связи.
Все мы слышали об AM радио и FM радио. Но фазовая модуляция, видимо, относится к другой категории – «PM радио» ни в коем случае не является распространенным термином. Оказывается, что фазовая модуляция более актуальна в контексте цифровой радиосвязи. Тем не менее, мы можем сказать, что PM радио так же распространено, как FM радио, просто потому, что между фазовой модуляцией и частотной модуляцией мало различий. ЧМ и ФМ лучше всего рассматривать как два тесно связанных варианта угловой модуляции, где «угол» относится к модификации величины, передаваемой функции синуса или косинуса.
Видео:Виды модуляцииСкачать

Математика
В предыдущей статье мы видели, что частотная модуляция достигается путем добавления интеграла низкочастотного модулирующего сигнала к аргументу функции синуса или косинуса (где функция синуса или косинуса представляет собой сигнал несущей):
Однако вы вспомните, что мы перешли к частотной модуляции, сначала обсуждая фазовую модуляцию: добавление самого низкочастотного модулирующего сигнала, а не его интеграла, заставляет фазу меняться в соответствии с амплитудой модулирующего сигнала. Таким образом, фазовая модуляция на самом деле немного проще частотной.
Как и в случае частотной модуляции, мы можем использовать индекс модуляции, чтобы сделать изменения фазы более чувствительными к изменениям амплитуды низкочастотного модулирующего сигнала:
Сходство между фазовой и частотной модуляциями становится более явным, если мы рассмотрим низкочастотный модулирующий сигнал, состоящий из одной частоты. Предположим, что xнч(t) = sin(ωнчt) . Интеграл синуса равен отрицательному косинусу (плюс константа, которую мы можем здесь игнорировать) – другими словами, интеграл представляет собой просто сдвинутую по времени версию исходного сигнала. Таким образом, если мы выполняем фазовую модуляцию и частотную модуляцию с помощью этого низкочастотного модулирующего сигнала, единственной разницей в модулированных сигналах будет выравнивание между амплитудой низкочастотного модулирующего сигнала и изменениями в сигнале несущей; сами изменения будут одинаковы. Это будет понятно в следующем разделе, где мы рассмотрим некоторые временны́е графики.
Важно иметь в виду, что мы имеем дело с мгновенной фазой, так же как частотная модуляция основана на концепции мгновенной частоты. Термин «фаза» довольно расплывчатый. Одно знакомое значение относится к начальному состоянию синусоиды; например «обычная» синусоида начинается со значения нуля и затем увеличивается в сторону своего максимального значения. Синусоида, которая начинается в другой точке своего периода, имеет сдвиг фазы. Мы можем также думать о фазе как о конкретной части полного периода сигнала, например, в фазе π/2 синусоида завершила одну четверть своего периода.
Эти интерпретации «фазы» нам не очень помогают, когда мы имеем дело с фазой, которая постоянно изменяется в зависимости от формы низкочастотного модулирующего сигнала. Скорее мы используем концепцию мгновенной фазы, т.е. фазы в заданный момент времени, которая соответствует значению, переданному (в заданный момент) тригонометрической функции. Мы можем думать об этих непрерывных изменениях в мгновенной фазе как о «толкании» значения несущей дальше или ближе к предыдущему состоянию формы волны.
Еще одна вещь, о которой нужно помнить: тригонометрические функции, включая синус и косинус, работают с углами. Изменение аргумента тригонометрической функции эквивалентно изменению угла, а это объясняет, почему и частотная, и фазовая модуляции описываются как угловая модуляция.
Видео:Частотное и временное представление сигналов. Спектр. МодуляцияСкачать

Временна́я область
Мы будем использовать те же сигналы, которые использовали при обсуждении FM, то есть несущую 10 МГц и низкочастотный модулирующий сигнал синусоиды 1 МГц:
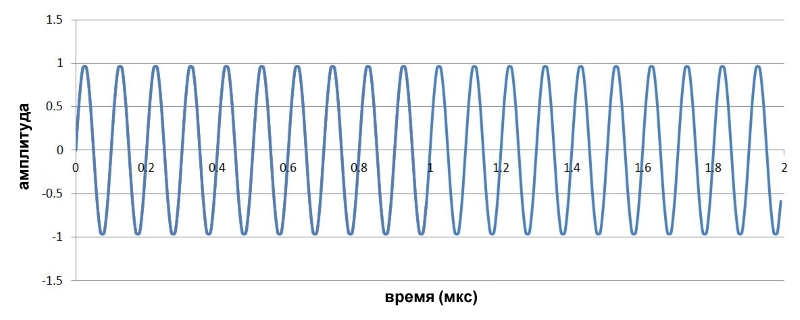
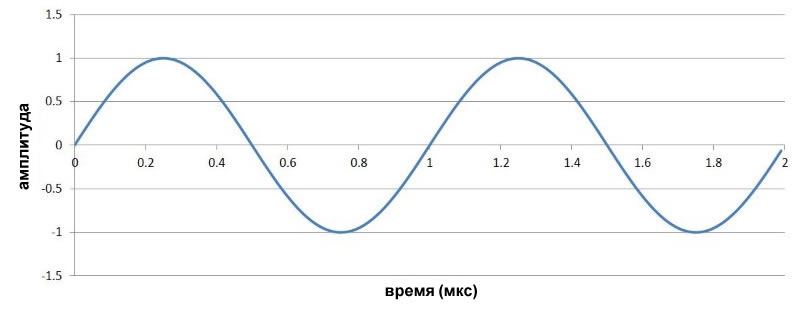
Ниже показан частотно-модулированный сигнал (с m=4), который мы видели в предыдущей статье:
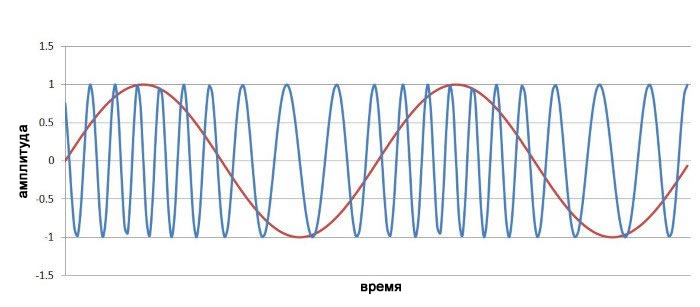
Мы можем рассчитать форму волны фазомодулированного сигнала, используя следующую формулу, где сигнал, добавленный к аргументу волны сигнала несущей, использует положительный синус (т.е. исходный сигнал) вместо отрицательного косинуса (т.е. интеграла исходного сигнала).
[ x_(t)=sin left( (10times10^6times2pi t)+sin(1times10^6times2pi t) right) ]
Ниже показан график сигнала с фазовой модуляцией:
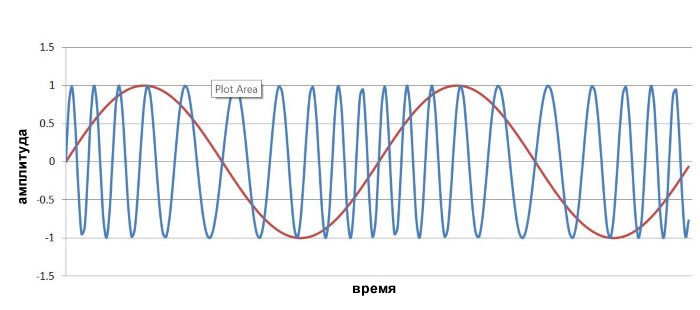
Прежде чем обсудить его, давайте посмотрим на диаграмму, которая одновременно показывает формы частотно-модулированного сигнала и фазомодулированного сигнала:
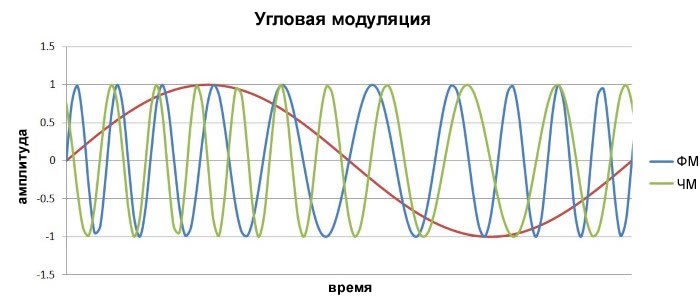
Первое, что здесь приходит в голову, это то, что с визуальной точки зрения частотная модуляция более интуитивно понятна по сравнению с фазовой модуляцией; существует четкая визуальная связь между участками с более высокой и низкой частотой и более высокими и более низкими уровнями низкочастотного модулирующего сигнала. В фазовой модуляции связь между низкочастотным модулирующим сигналом и поведением несущей, возможно, не сразу очевидна. Однако после небольшого осмотра мы видим, что частота несущей в фазовой модуляции соответствует наклону формы волны модулирующего сигнала, наиболее высокочастотные участки соответствуют времени самого крутого положительного наклона xнч , а наиболее низкочастотные участки соответствуют времени самого крутого отрицательного наклона.
Это имеет смысл. Напомним, что частота (как функция времени) является производно фазы (как функции времени). При фазовой модуляции наклон формы низкочастотного модулирующего сигнала определяет, как быстро изменяется фаза, и скорость изменения фазы эквивалентна частоте. Поэтому в фазомодулированном сигнале высокий наклон модулирующего сигнала соответствует высокой частоте, а низкий наклон модулирующего сигнала соответствует низкой частоте. В частотной модуляции мы используем интеграл от xнч , который приводит к сдвигу высокочастотных (или низкочастотных) участков несущей к значениям модулирующего сигнала, следующих после высоких (или низких) наклонных участков формы низкочастотного модулирующего сигнала.
Видео:фазовая модуляцияСкачать

Частотная область
Предыдущие графики во временной области демонстрируют сказанное ранее: частотная модуляция и фазовая модуляция очень похожи. Поэтому неудивительно, что эффект от фазовой модуляции в частотной области аналогичен эффекту от частотной модуляции. Ниже представлены спектры сигналов с фазовой модуляцией с использованием сигнала несущей и низкочастотного модулирующего сигнала, используемых выше:
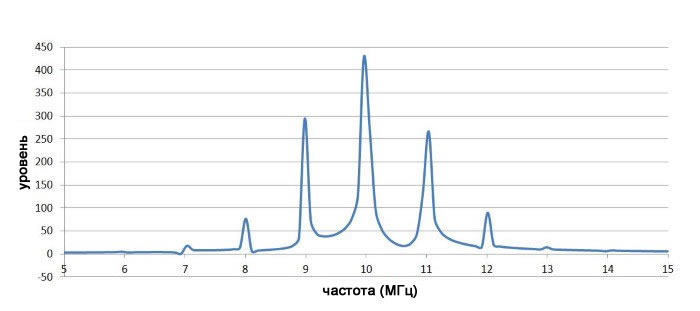
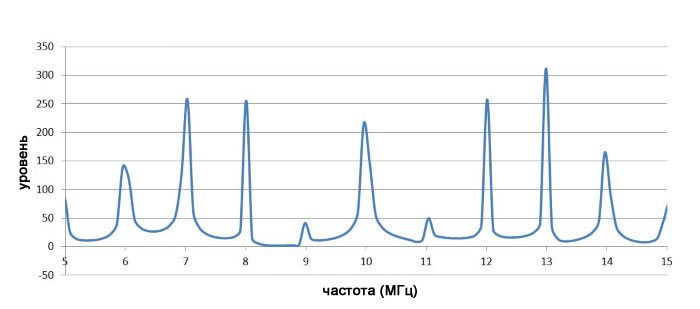
Видео:Фазовое разделение каналовСкачать

Фазовая модуляция.
При фазовой модуляции (ФМ) передаваемое сообщение изменяет значение фазы несущей. Фаза несущей изменяется пропорционально мгновенным значениям тока или напряжения модулируемого сообщения по закону
где Аф — максимальный сдвиг по фазе или девиация фазы.
При увеличении значений тока и напряжения (сообщения) частоты возникает опережение по фазе на величину Дфвт^Й, а при уменьшении — отставание по фазе.
Значение ФМ — колебания:
аналогично S4M(t) с той лишь разницей, что при ФМ индекс модуляции:
При ФМ изменяется не только фаза, но и мгновенная частота несущей. Точно также при ЧМ изменяется и фаза несущей. Таким образом, ФМ и ЧМ в какой — то мере аналогичны и отличаются друг от друга методами осуществления.
На рис. 4.10 показан принцип формирования ФМ — сигнала. Сравнение рисунков 4.7 и 4.10 говорит о том, что сигналы с ЧМ и ФМ различаются весьма незначительно.
Рис. 4.10. Формирование ФМ сигнала Так как ФМ и ЧМ связаны, поэтому они могут быть объединены как угловая модуляция:
Математическая модель однотональных ЧМ и ФМ сигналов с любым значением индекса модуляции m в общем случае одинакова и определяется выражением (4.9).
Индекс угловой модуляции равен отношению девиации частоты к частоте модулирующего сигнала:
Различия между частотной и фазовой модуляцией проявляются при изменении частоты Q модулирующего сигнала.
При фазовой модуляции девиация частоты прямо пропорциональна Q, а индекс угловой модуляции от частоты модулирующего сигнала не зависит:
Напротив, при ЧМ постоянным параметром модуляции является девиация частоты, а индекс модуляции обратно пропорционален частоте модулирующего сигнала
Спектр ФМ сигнала имеет практически такой же вид как и спектр ЧМ сигнала. Полоса частот при ФМ модуляции определяется выражением:
Так как при ЧМ индекс модуляции уменьшается с увеличением частоты сообщения, а при ФМ он не зависит от неё, то ширина полосы частот при ФМ оказывается больше, чем при ЧМ. При m « 1 спектр частот ЧМ и ФМ состоит из несущей и двух боковых полос как при AM с ДБП. При ш » 1 спектр частот ФМ схож со спектром при ЧМ с той лишь разницей, что при ФМ боковые частоты не зависят от частоты сообщения, тогда как при ЧМ амплитуда этих частот уменьшается с увеличением частоты сообщения.
🔥 Видео
Осипов М.Н. - Фазовая модуляция (часть)Скачать

Угловая модуляцияСкачать

Фазовая модуляцияСкачать

09 Фаз диагр двухкомп сист 1 принципы и мех смесьСкачать
Угловая модуляция (фазовая и частотная)Скачать

Аналоговая модуляция. АМ ЧМ ФМСкачать

Фазовая модуляция на ПЛИССкачать

Лекция 8. Кодирование, модуляция и манипуляция сигналов.Скачать

Теория: радиоволны, модуляция и спектр.Скачать

Реальная схема фазового модулятора с тремя взаимосвязанными контурамиСкачать

Модуляция, детектирование. 11 класс.Скачать

Частотное разделение каналовСкачать
Дискретные виды модуляции (манипуляция)Скачать

физика 10-11 база. лекция 28. Принципы радиосвязиСкачать

Амплитудная модуляцияСкачать