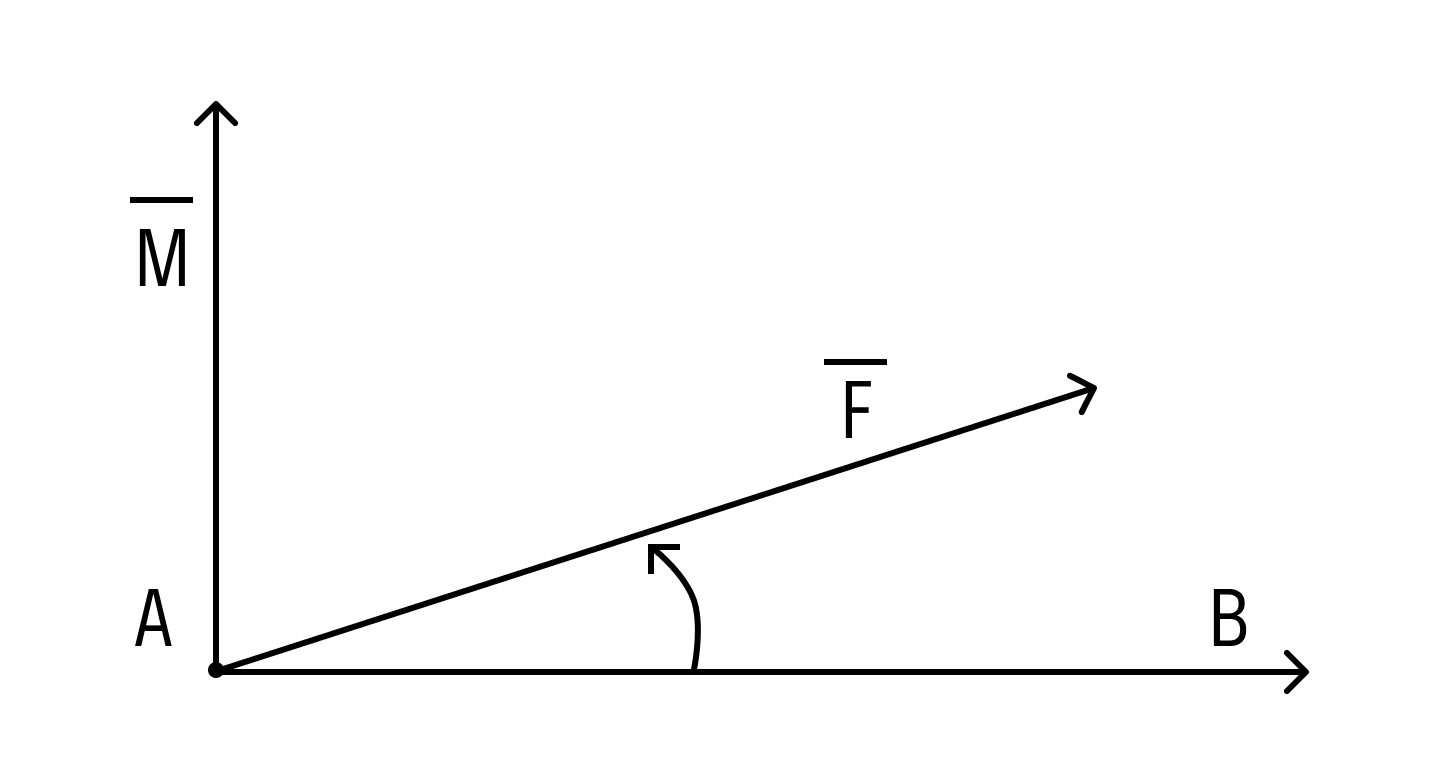
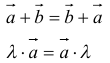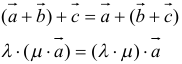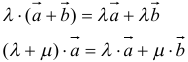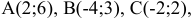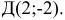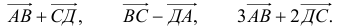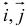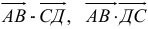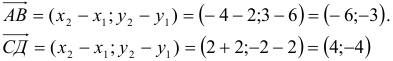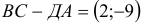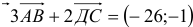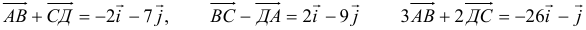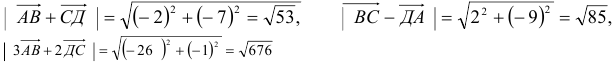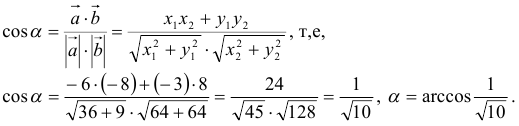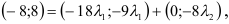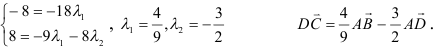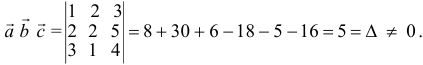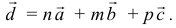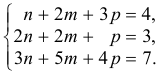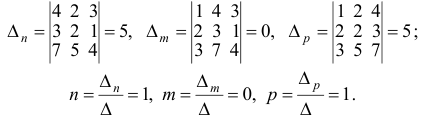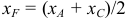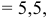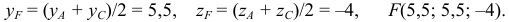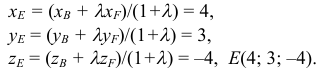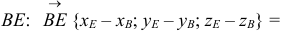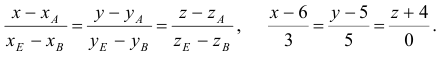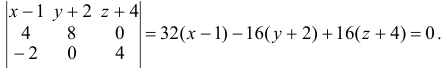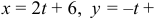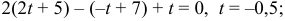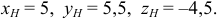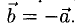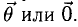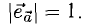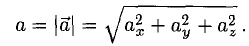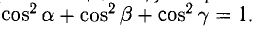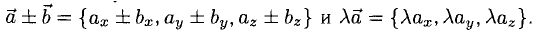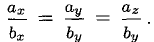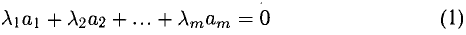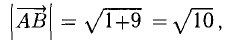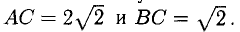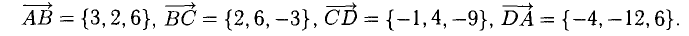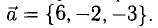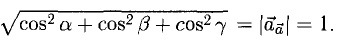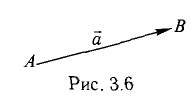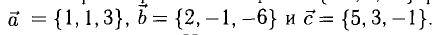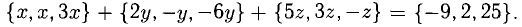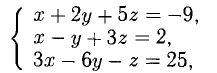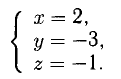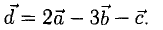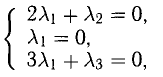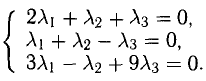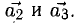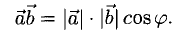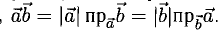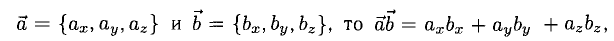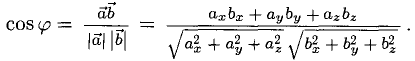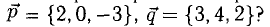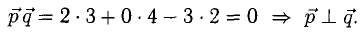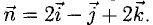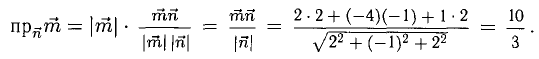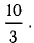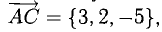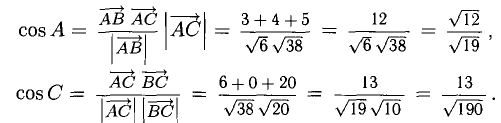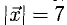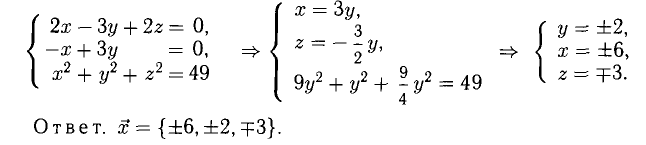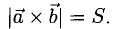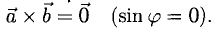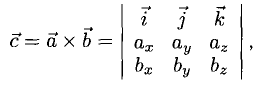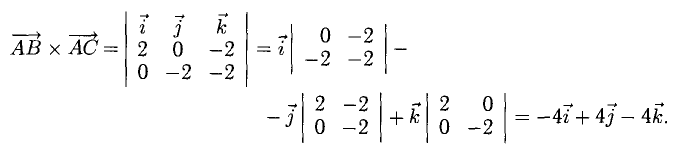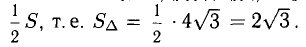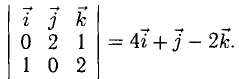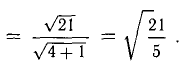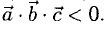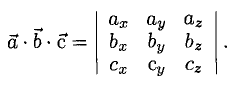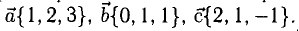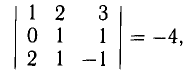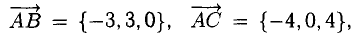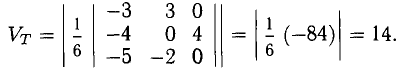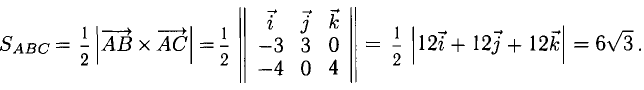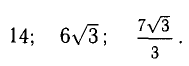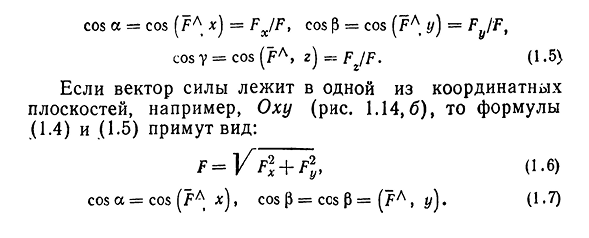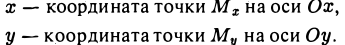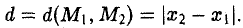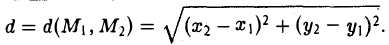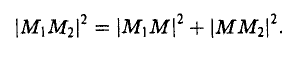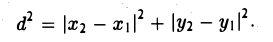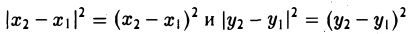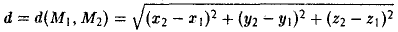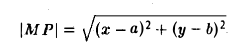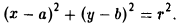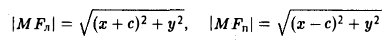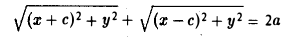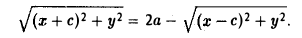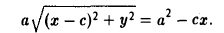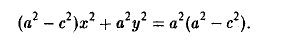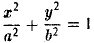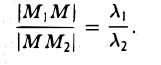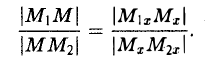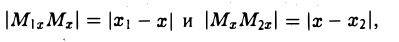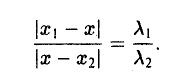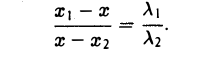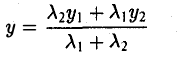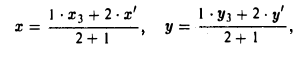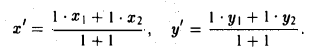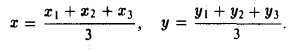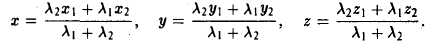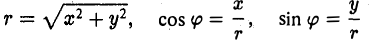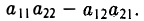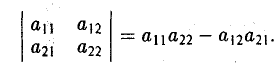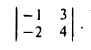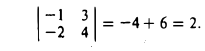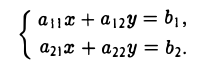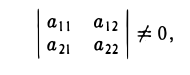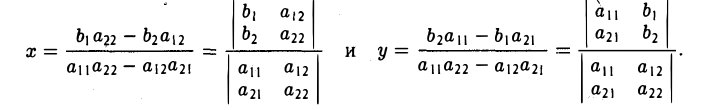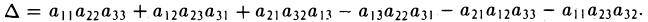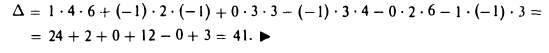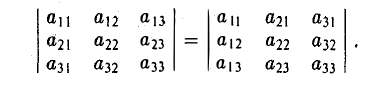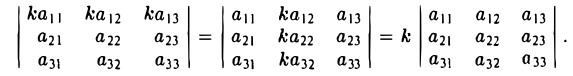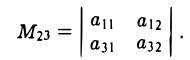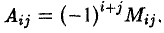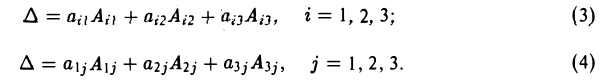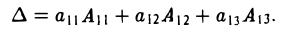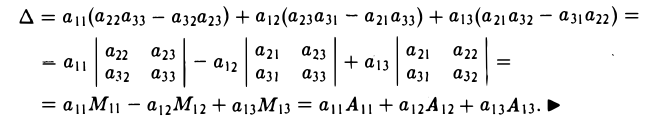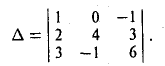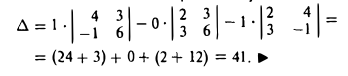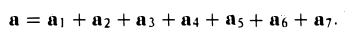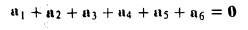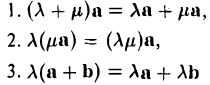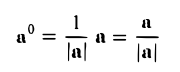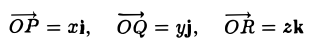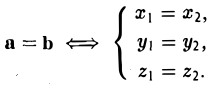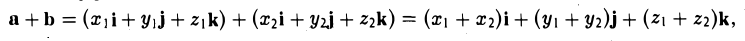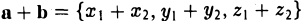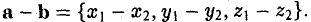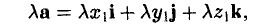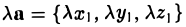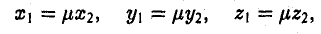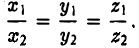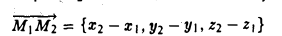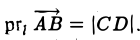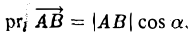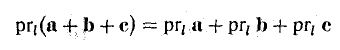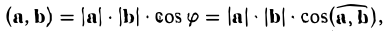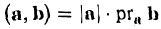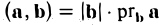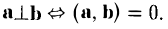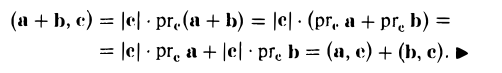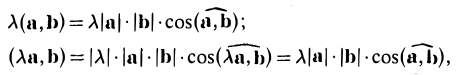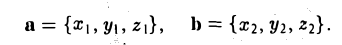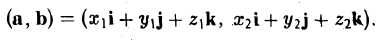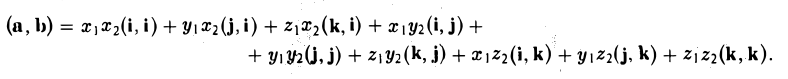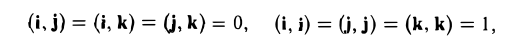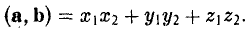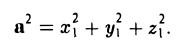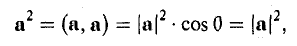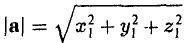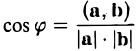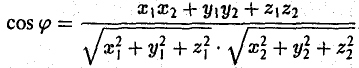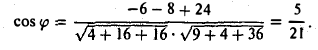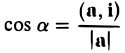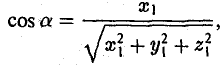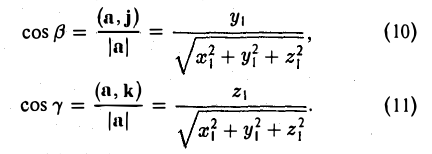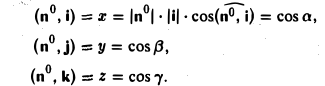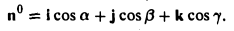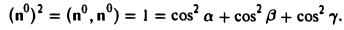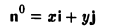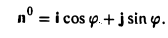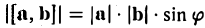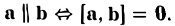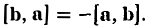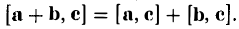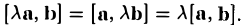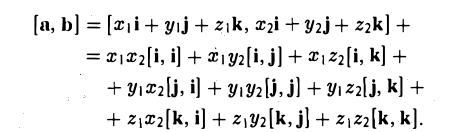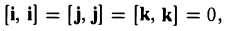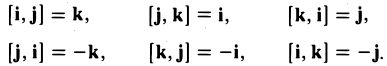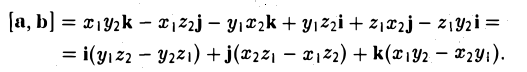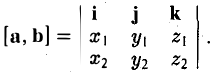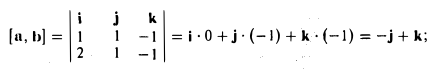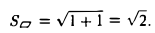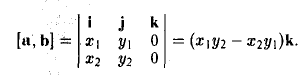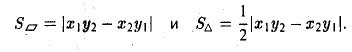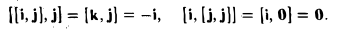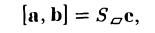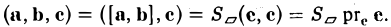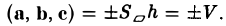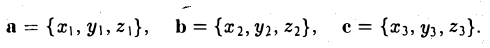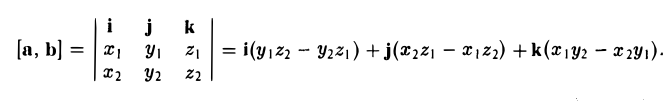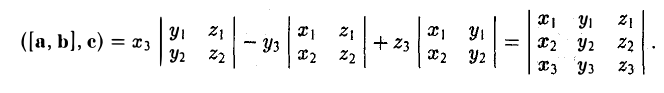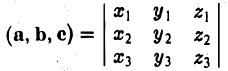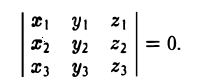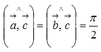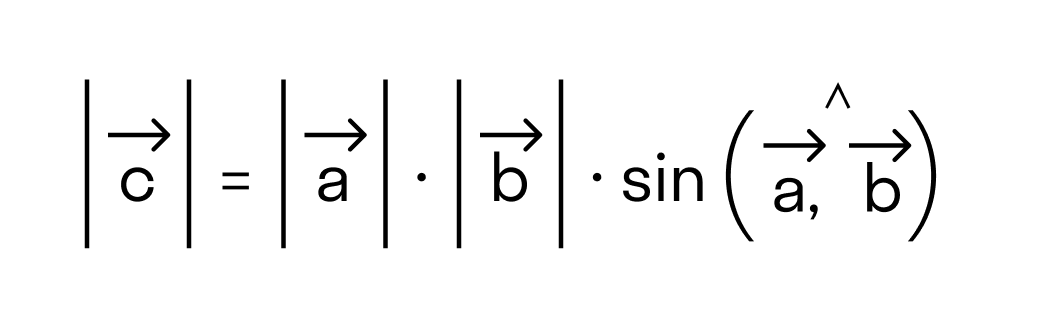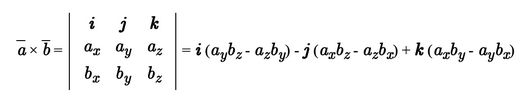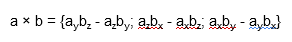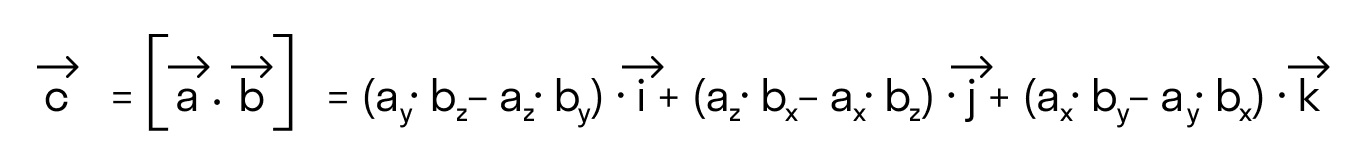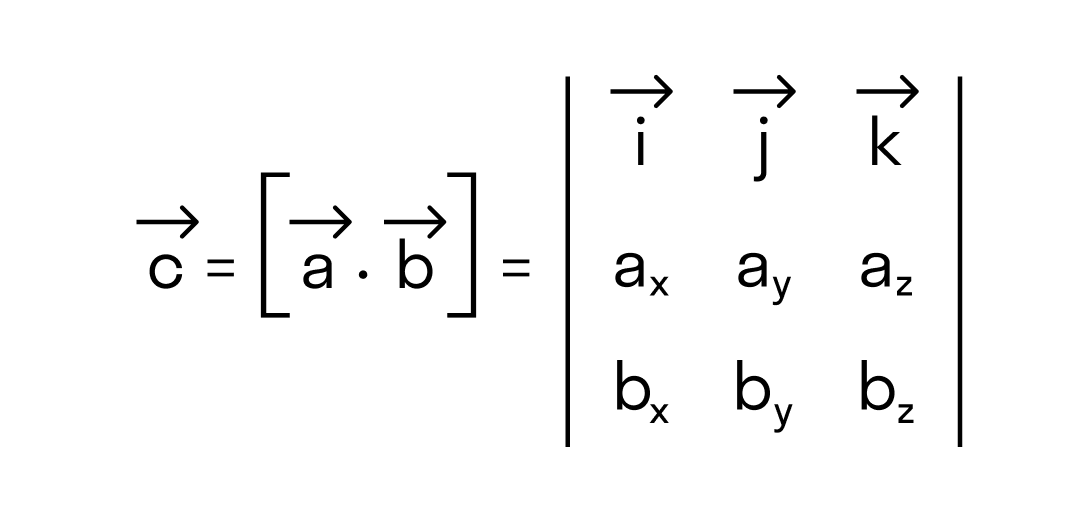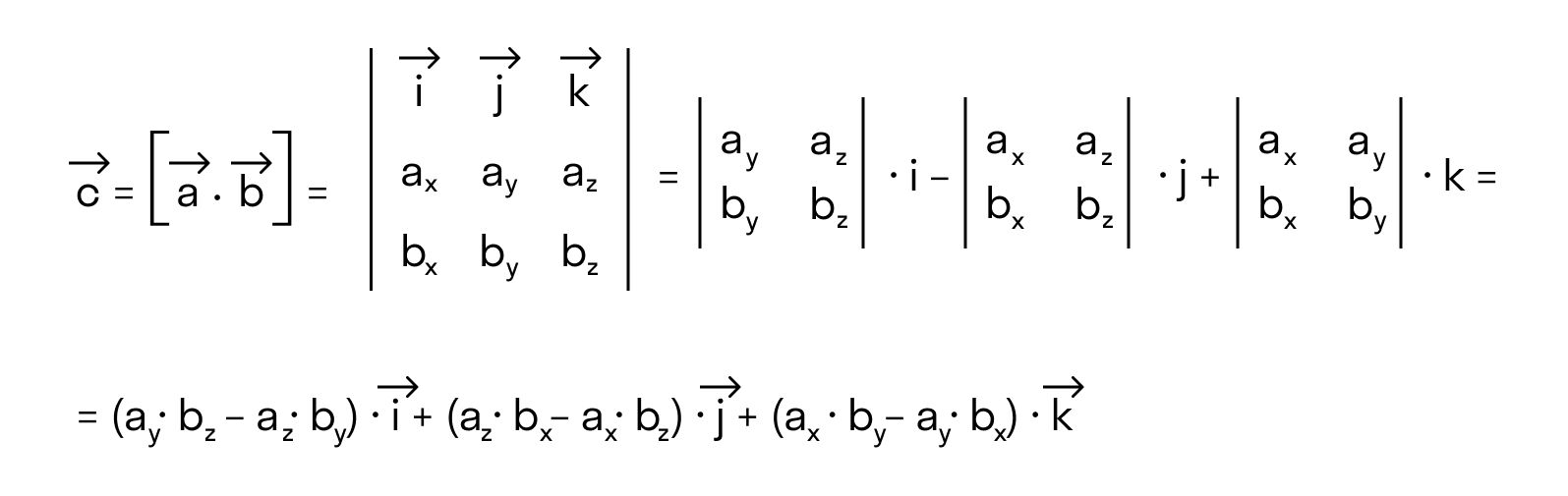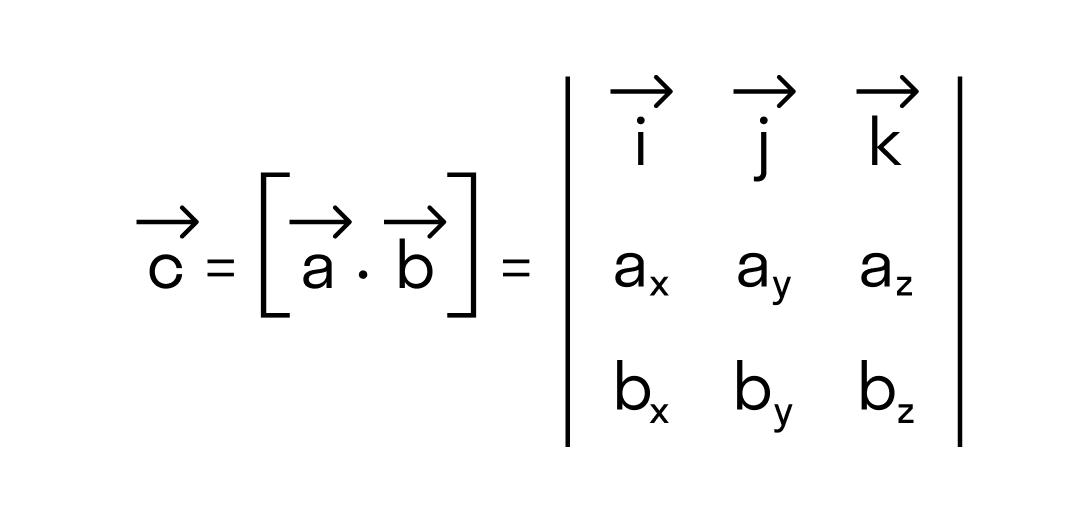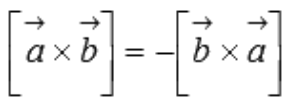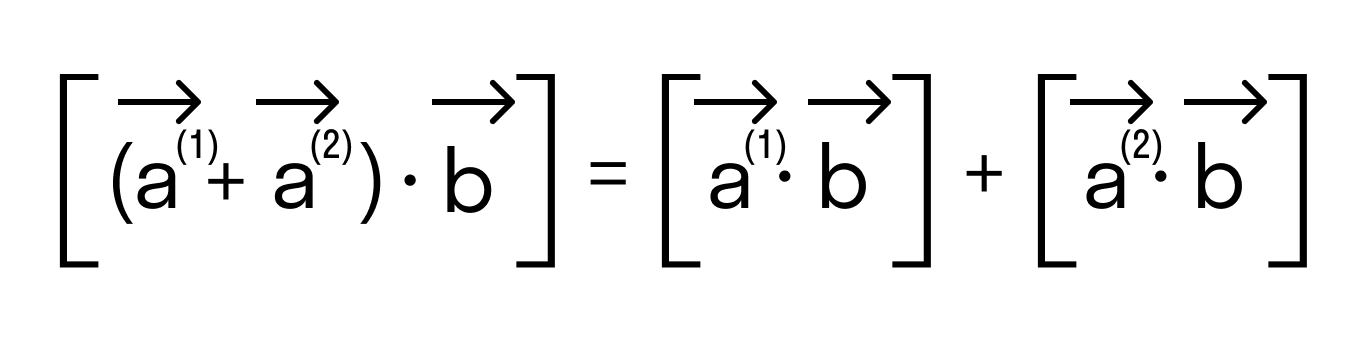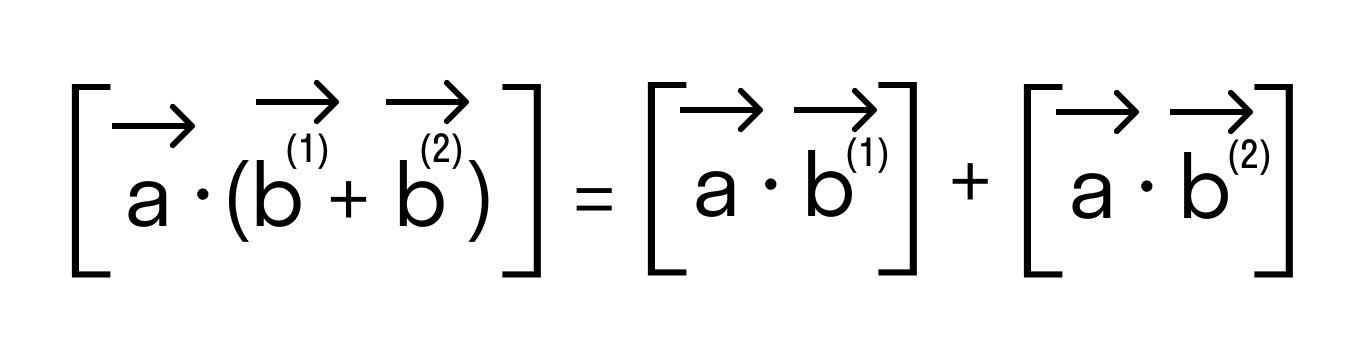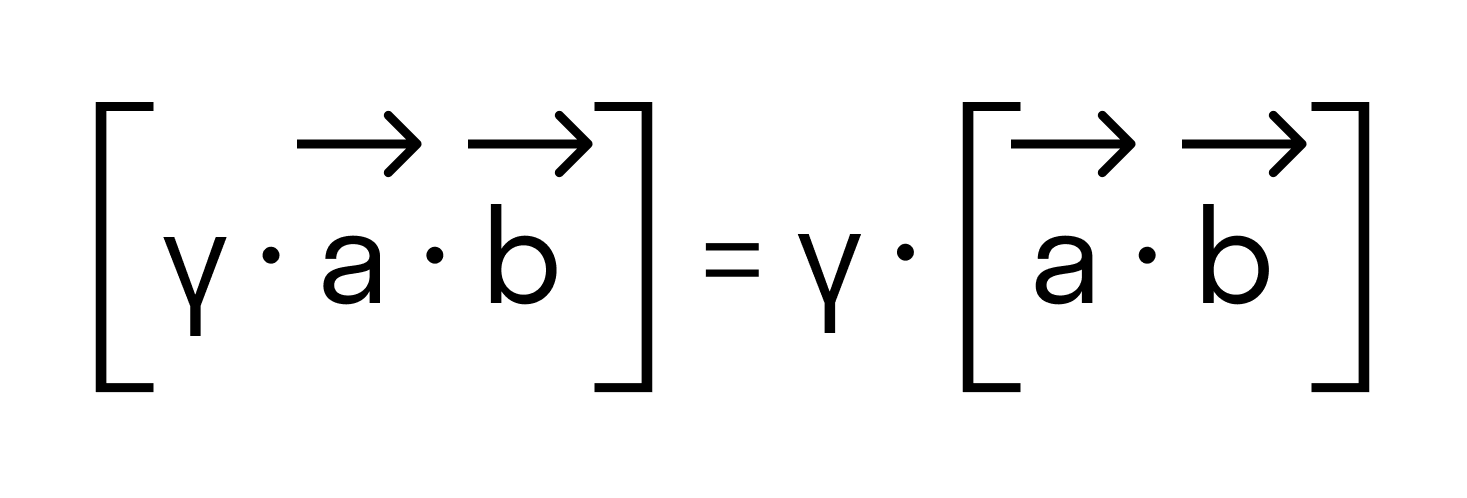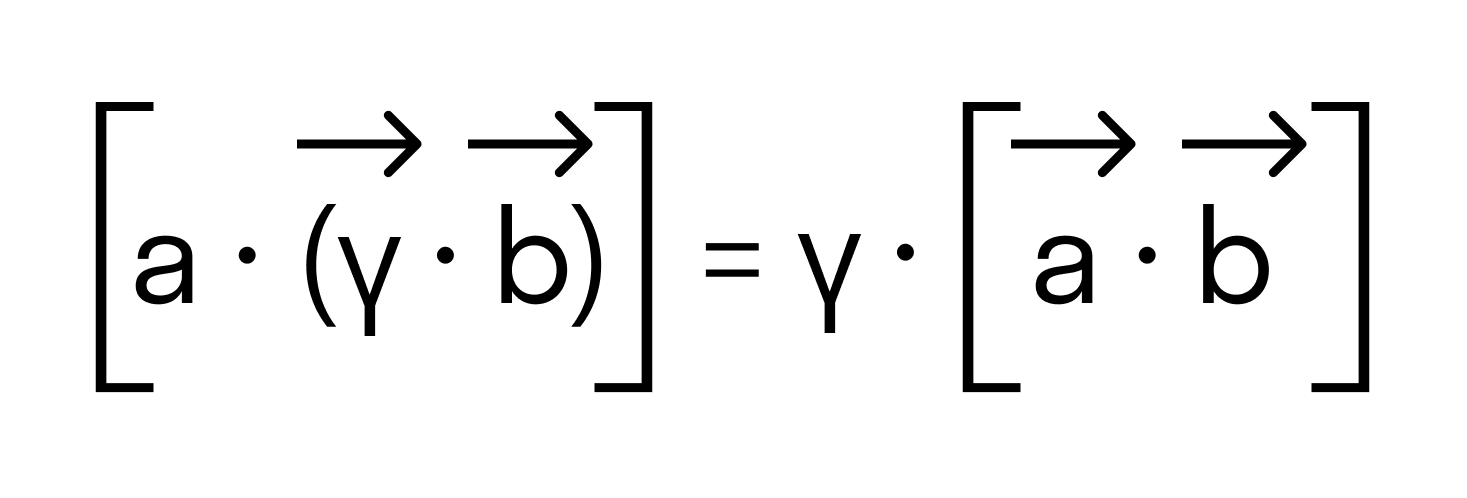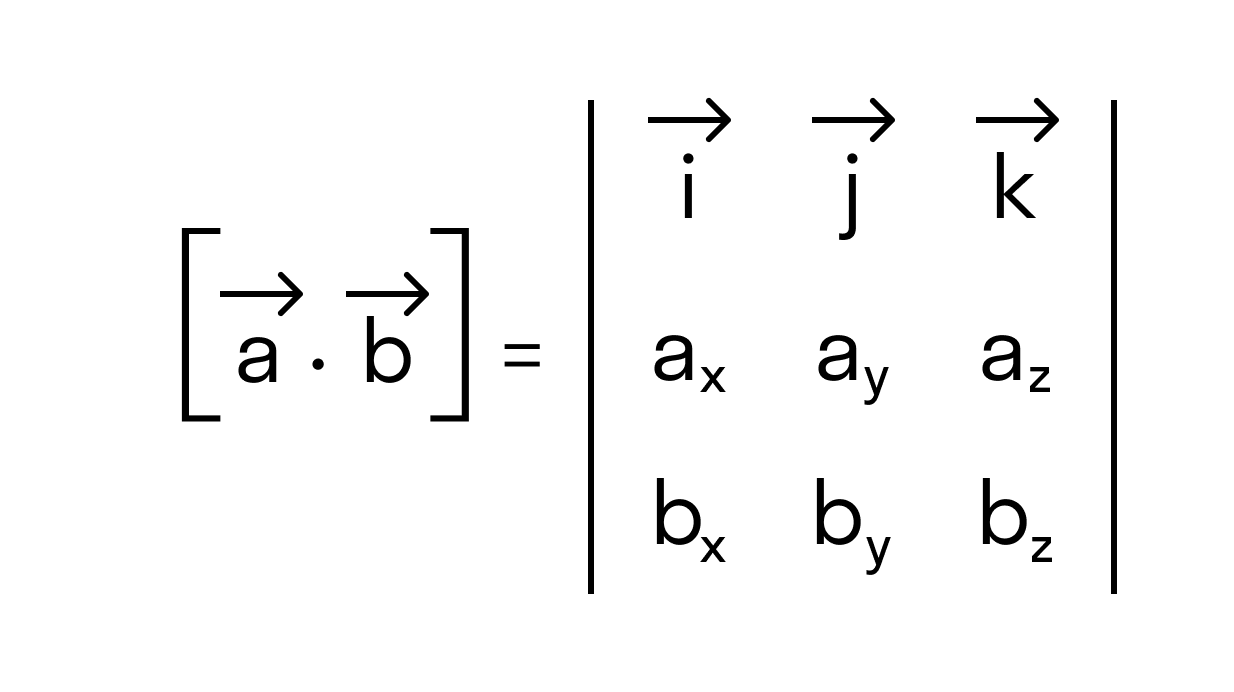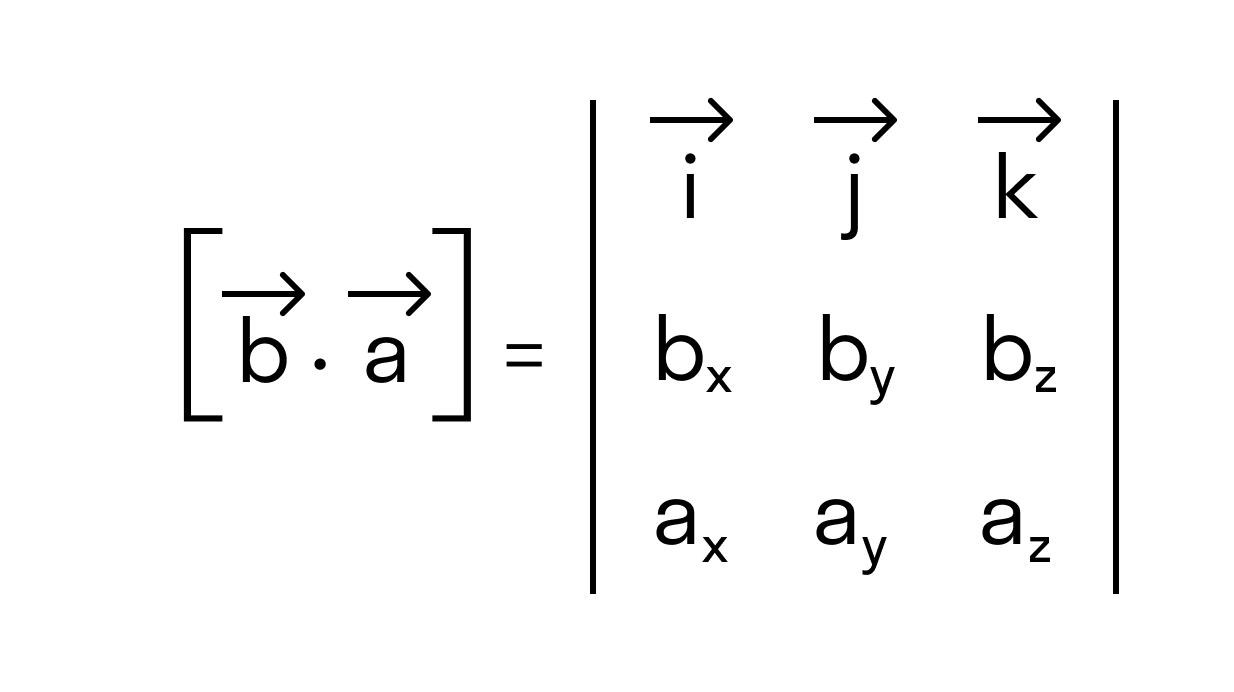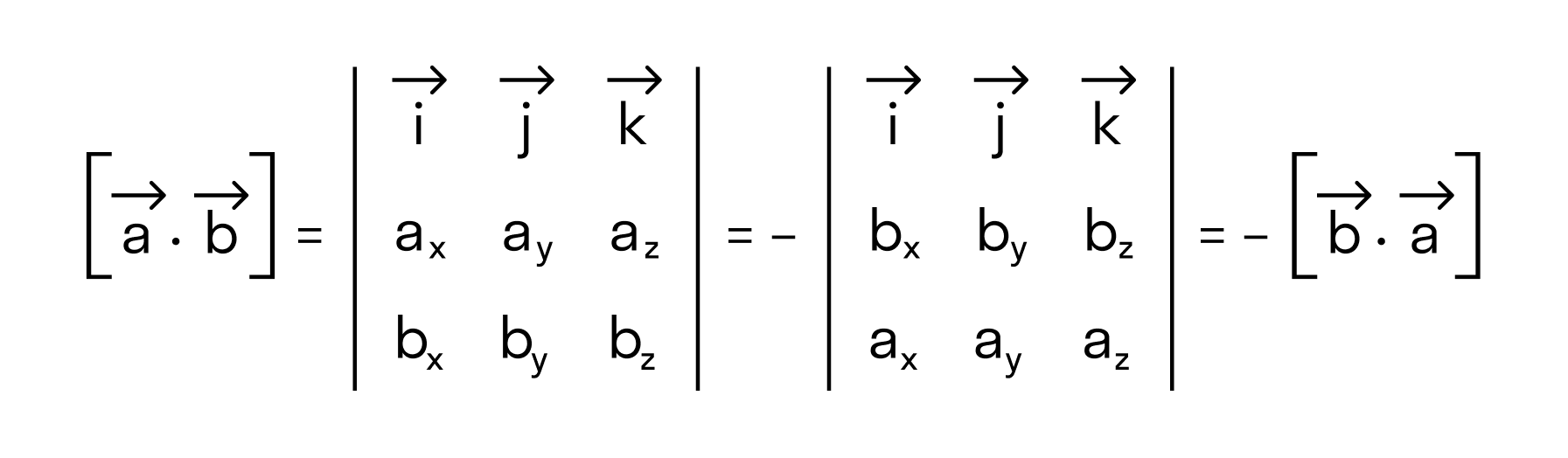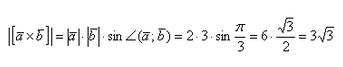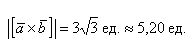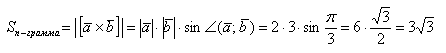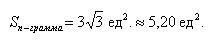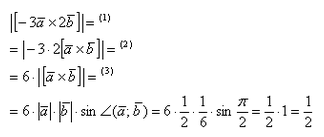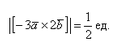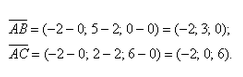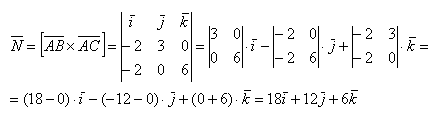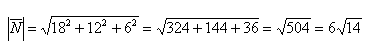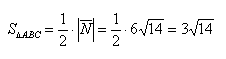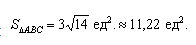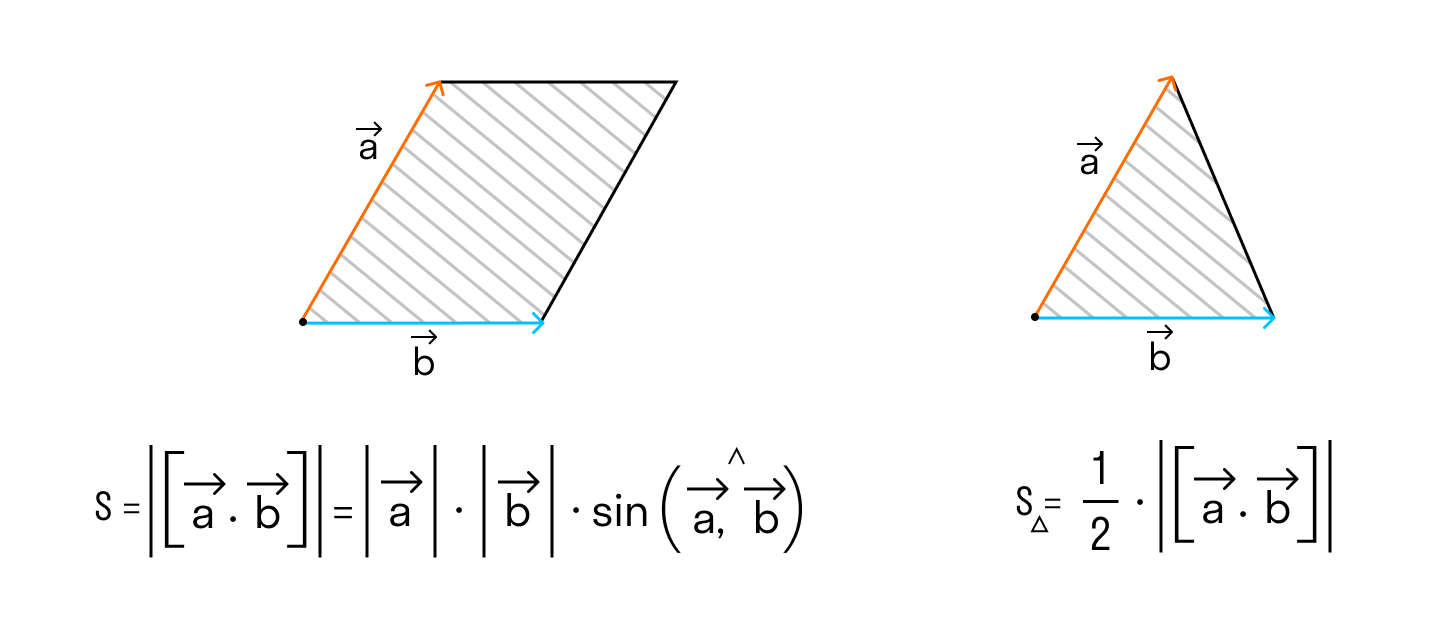Вектором называется направленный отрезок. Вектор обозначается либо символом 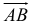
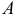
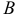

2. Длиной (модулем) вектора 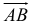
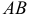
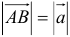
3.Вектор называется единичным, если его длина равна «1»; единичный вектор 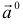


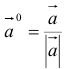
4. Вектор называется нулевым, если его начало и конец совпадают 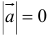
5. Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Коллинеарность векторов обозначается: 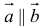

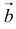
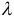
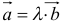
6. Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и направление.
7. Вектор 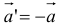

8. Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Для решения задач необходимо уметь выполнять линейные операции над вектором в геометрической форме, то есть над вектором, как над
направленным отрезком: сложение, вычитание векторов и умножение вектора на число.
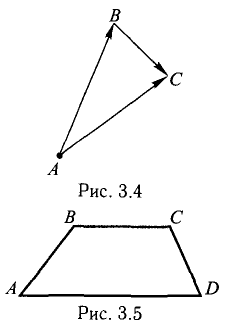
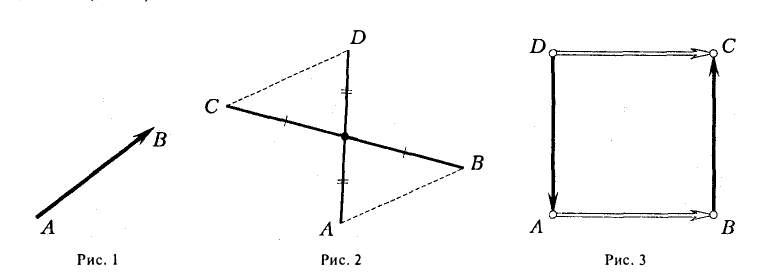
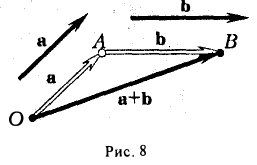
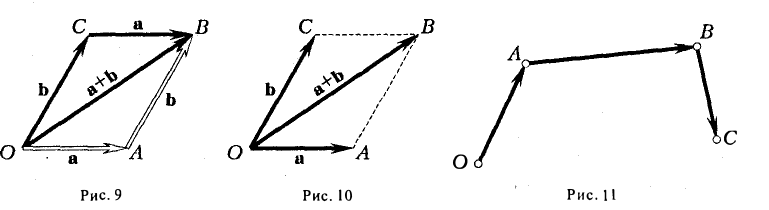
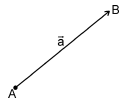
9. Сложение двух векторов можно выполнить по правилу параллелограмма (рис. 1) или по правилу треугольника (рис. 2).
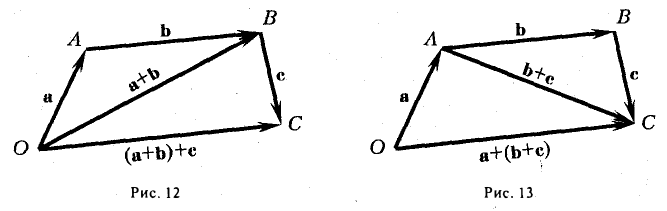
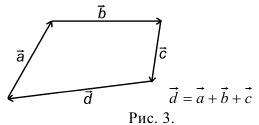
При сложении более двух векторов, лежащих в одной плоскости, используется правило «замыкающей линии многоугольника» (рис. 3).
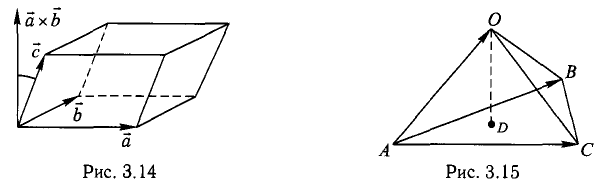
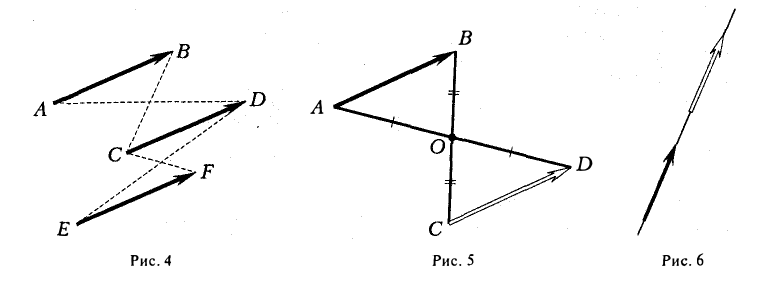
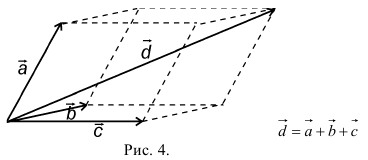
При сложении трех некомпланарных векторов удобно пользоваться правилом «параллелепипеда» (рис. 4).
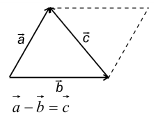
10. Действие вычитания двух векторов связано с действием сложения (рис.5).
Разностью двух векторов называется вектор, проведенный из конца вычитаемого в конец уменьшаемого. Заметим, что разностью является вектор, служащий второй диагональю параллелограмма.
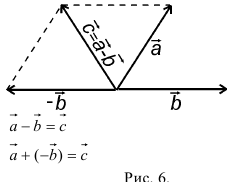
Разность можно также представить в виде сложения с противоположным вектором (рис. 6).
11. Произведением вектора 
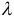
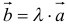
- модуль, равный
;
- направление, одинаковое с
, если
.
- направление, противоположное с
, если
.
12. Для решения задач полезно знать также следующие законы и свойства:
- переместительный:
- сочетательный:
- распределительный:
- Примеры задач решаемых с применением векторной алгебры
- Векторная алгебра — решение заданий и задач по всем темам с вычислением
- Понятие вектора. Линейные операции над векторами
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Основные понятия векторной алгебры
- Прямоугольные декартовы координаты
- Координатная ось
- Прямоугольные декартовы координаты на плоскости
- Прямоугольные декартовы координаты в пространстве
- Полярные координаты
- Определители 2-го и 3-го порядков
- Понятия связанного и свободного векторов
- Линейные операции над векторами
- Сложение векторов
- Умножение вектора на число
- Координаты и компоненты вектора
- Линейные операции над векторами в координатах
- Проекция вектора на ось
- Основные свойства проекций
- Скалярное произведение векторов
- Свойства скалярного произведения
- Скалярное произведение векторов, заданных координатами
- Косинус угла между векторами. Направляющие косинусы
- Векторное произведение векторов
- Свойства векторного произведения
- Векторное произведение векторов, заданных координатами
- Смешанное произведение векторов
- Геометрический смысл смешанного произведения
- Смешанное произведение в координатах
- Двойное векторное произведение
- Векторное произведение векторов
- Определение векторного произведения
- Координаты векторного произведения
- Свойства векторного произведения
- Примеры решения задач
- Пример 1
- Пример 2
- Пример 3
- Геометрический смысл векторного произведения
- Физический смысл векторного произведения
- Векторный метод в курсе геометрии основной школы
- 🎬 Видео
Видео:Урок 320. Производная функции и ее геометрический смыслСкачать

Примеры задач решаемых с применением векторной алгебры
Задача:
Пусть даны точки
1) Найти координаты векторов
2) Написать разложение этих векторов по базису
3) Найти длины этих векторов
4) Найти скалярное произведение
5) Найти угол между векторами 

6) Найти разложение вектора 

Решение:
1) Вычислим координаты векторов 
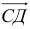
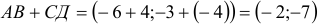
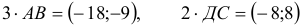
2)
4) Для вычисления угла между векторами воспользуемся формулой:
5) Разложить вектор 

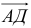


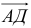
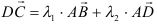
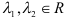
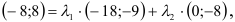
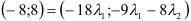
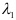
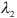
Задача:
а). Даны векторы 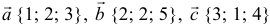
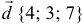
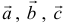
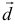
Решение:
Три вектора образуют базис, если 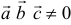
Найдем координаты вектора 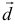
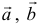
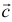
Два вектора равны, если их соответствующие координаты равны.
Решим систему методом Крамера:
Ответ: 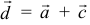
Задача:
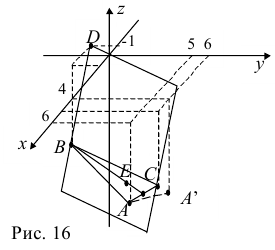
Даны координаты вершин тетраэдра 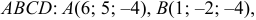
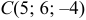
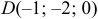
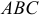

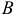
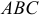


Решение:
1) Найдем координаты т. 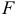
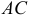
Точка 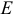
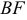
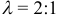
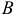
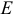
2) Найдем направляющий вектор прямой 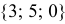

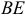
3) Найдем уравнение плоскости 
Найдем каноническое уравнение прямой, перпендикулярной плоскости 

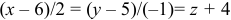
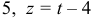
Найдем координаты точки 

Координаты точки 


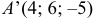
Ответ: 1) координаты точки пересечения медиан 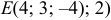
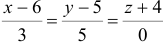
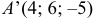
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Возможно вам будут полезны эти страницы:
Видео:Аналит. Экстренный выпуск #02 Векторные уравненияСкачать

Векторная алгебра — решение заданий и задач по всем темам с вычислением
Понятие вектора. Линейные операции над векторами
1°. Любые две точки 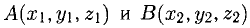
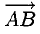
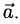
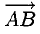
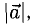
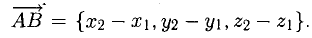
Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными.
Два вектора 
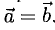
Векторы 
Вектор называется нулевым, если его модуль равен нулю, и обозначается
2°. Линейными называются действия сложения, вычитания векторов и умножения вектора на число.
1.Если начало 

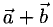


2.Если начала векторов 




3.При умножении вектора 
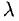
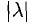
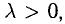
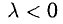
Вектор 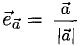

3°. Запись ci — 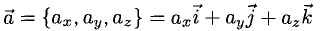

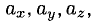

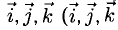
4°. Числа 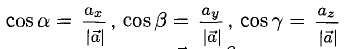
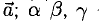

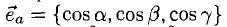

5°. Линейные операции над векторами, которые заданы своими координатами, определяются так: пусть 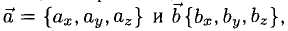
Следовательно, при сложении векторов складываются их соответствующие координаты, а при умножении вектора на число умножаются на число все координаты вектора.
6°. Необходимое и достаточное условие коллинеарности векторов 
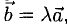
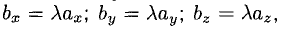
Если один из членов какого-нибудь из этих отношений равен нулю, то и второй член того же отношения должен быть нулем. Геометрически это значит, что в этом случае оба вектора перпендикулярны соответствующей координатной оси (например, если 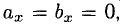
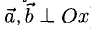
7°. Система векторов 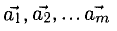
( 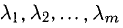

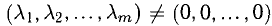
Примеры с решениями
Пример:
Доказать, что треугольник с вершинами в точках A(1,2), B(2,5), С(3,4) прямоугольный.
Решение:
Построим векторы, совпадающие со сторонами треугольника (см. п. 1°): 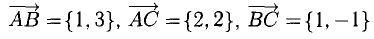
Найдем длины сторон: 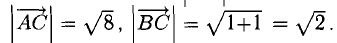
Нетрудно видеть, что 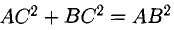
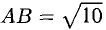
Пример:
Проверить, что точки А( 2,-4,3), В(5, —2,9), С( 7,4,6) и D(6,8, -3) являются вершинами трапеции.
Решение:
Составим векторы-стороны с целью обнаружения коллинеарности векторов (в трапеции ВС || AD) (рис. 3.5):
Имеем 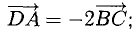
Пример:
Найти орт и направляющие косинусы вектора
Решение:
Имеем 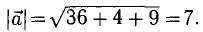
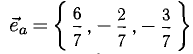
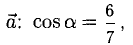
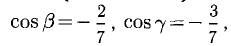
Пример:
Определить точку В, которая является концом вектора 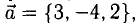
Решение:
Пусть точка В имеет координаты B(x,y,z) (рис. 3.6). Тогда координа- ^ ты вектора (п. 1°)
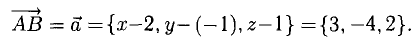
Следовательно, 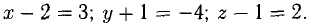
Пример:
Вектор 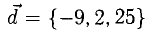
Решение:
Необходимо найти такие числа х, у, z, что 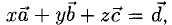
Имея в виду, что при сложении векторов складываются их координаты и равные векторы имеют равные координаты, приходим к системе уравнений
Ответ.
Пример:
Показать, что система векторов 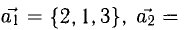
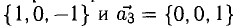
Решение:
В данном случае равенство (1) имеет вид 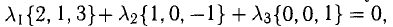
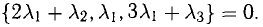
из которой следует, что 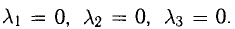
Пример:
Показать, что система векторов 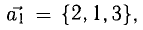
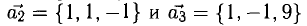
Решение:
Равенство (1) равносильно системе уравнений
Она имеет ненулевое решение, например, 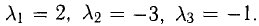
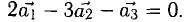
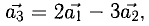
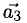
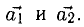
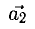
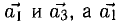
Скалярное произведение векторов
1°. Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению их длин на косинус угла 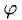
Из 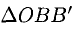
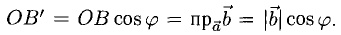
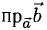


Итак,
т.е. скалярное произведение векторов равно сумме произведений одноименных координат этих векторов.
При этом 
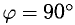
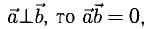
3°. Из определения скалярного произведения следует формула для вычисления угла между двумя векторами:
Примеры с решениями
Пример:
Перпендикулярны ли векторы 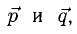
Решение:
Условие перпендикулярности векторов (п. 2°) 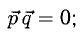
Пример:
Найти проекцию вектора 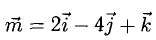
Решение:
Имеем 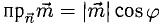
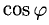
Ответ
Пример:
Зная векторы, совпадающие с двумя сторонами: 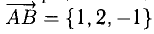
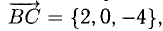
Решение:
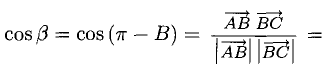
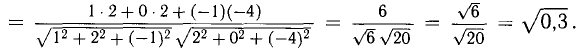
При помощи таблиц находим 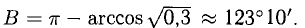
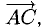
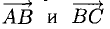
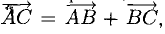
Ответ. 123° 10′, 19°29′, 37°21′.
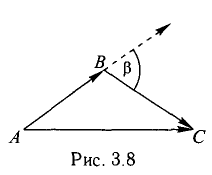
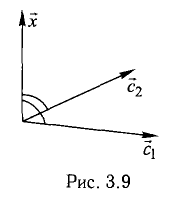
Пример:
Найти координаты вектора 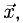
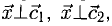
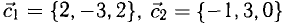
Решение:
На рис. 3.9 имеем 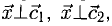
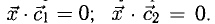
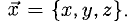
Векторное произведение векторов
1°. Векторы 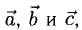

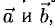
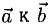
2°. Векторным произведением ненулевых векторов 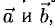

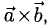
1) 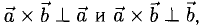
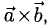
2) Вектор 
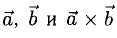
3) 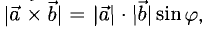
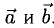
Если векторы 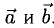

3°. Если известны координаты векторов-сомножителей 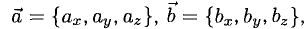
в которой определитель следует разложить по элементам первой строки.
Примеры с решениями
Пример:
Найти площадь треугольника, вершины которого находятся в точках А(1,2,3), В<3,2,1), С(1,0,1).
Решение:
Найдем координаты векторов 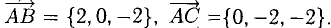
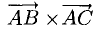
Найдем длину этого вектора, которая равна численно площади параллелограмма S (п. 2°): 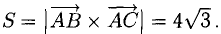
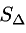
Пример:
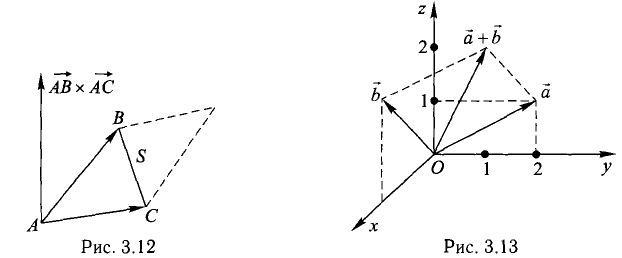
Построить параллелограмм на векторах 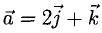
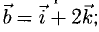

Сделаем чертеж (рис. 3.13). Имеем 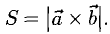
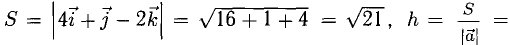
Смешанное произведение векторов
1°. Смешанным произведением трех ненулевых векторов 


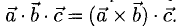

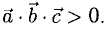

Модуль смешанного произведения векторов 
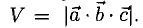
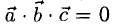

Объем тетраэдра с вершинами в точках 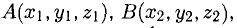
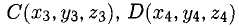
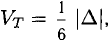
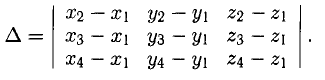
2°. Условие 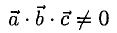

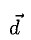
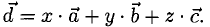
Примеры с решениями
Пример:
Найти объем параллелепипеда, построенного на векторах
Решение:
Искомый объем 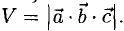
Пример:
В точках 0(0,0,0), А(5,2,0), В(2,5,0) и С(1,2,4) находятся вершины пирамиды. Вычислить ее объем, площадь грани ABC и высоту пирамиды, опущенную на эту грань.
Решение:
1) Сделаем схематический чертеж (рис. 3.15).
2) Введем векторы 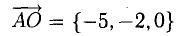
3) Площадь грани ABC
4) Объем пирамиды 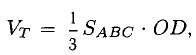
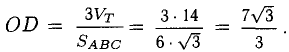
Ответ.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Основные понятия векторной алгебры




Видео:Геометрический смысл производной. Уравнение касательнойСкачать

Прямоугольные декартовы координаты
Координатная ось
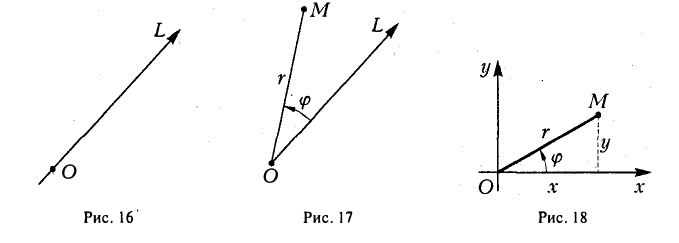
Пусть на плоскости или в пространстве задана произвольная прямая L: Ясно, что по этой прямой L сы можем перемещаться в oднoм из двух противоположных направлений. Выбор любого (одного) из этих направлений будем называть ориентацией прямой L.
Оnределение:
Прямая с заданной на ней ориентацией называется осью. На чертеже ориентация оси указывается стрелкой (рис. 1 ) . Фиксируем на оси 
Пусть М — произвольная точка оси 
Оnределение:
Ось 
Прямоугольные декартовы координаты на плоскости
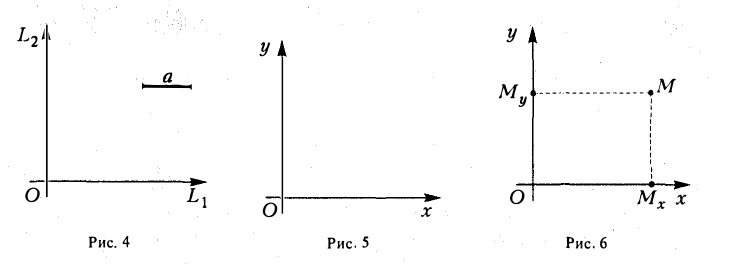
Пусть П — произвольная плоскость. Возьмем на ней некоторую точку О и проведем через эту точку взаимно перпендикулярные прямые L 1 и L 2. Зададим на каждой из nрямых L 1 и L 2 ориентацию и выберем единый масштабный отрезок а. Тогда эти прямые nревратятся в координатные оси с общей точкой отсчета О (рис. 4).
Назовем одну из координатных осей осью абсцисс (осью Ох), друrую —осью ординат (осью Оу) (рис. 5). Точка О называется началом координат. Пусть М — произвольная точка плоскости П (рис. 6). Проведем через точку М прямые, перпендикулярные координатным осям, и поставим ей в соответствие упорядоченную пару чисел (х, у) по следующему nравилу:
Числа х и у называются прямоугольными декартовыми при этом х называется ее абсциссой, а у — ординатой. координатами точки М; Обозначение: М(х, у). Чтобы кратко охарактеризовать описанную конструкцию, говорят, что на плоскости П задана прямоугольная декартова система координат Ох у. Координатные оси разбивают плоскость на четыре части, называемые четвертями или квадрантами. На рисунке и в таблице показано, как эти квадранты нумеруются (рис. 7).
Замечание:
Масштабные от резки на координатных осях могут быть и разной длины. В этом случае координатная система называется просто прямоугольной.
Прямоугольные декартовы координаты в пространстве
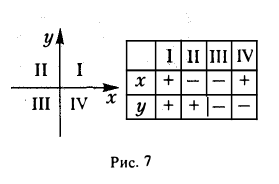
Возьмем в пространстве некоторую точку О и проведем через нее три взаимно перпендикулярные прямые L 1 , L 2 и L 3 . Выберем на каждой из nрямых ориентацию и единый масштаб. Прямые L 1 , L 2 и L 3 превратятся в координатные оси с общей точкой отсчета О (рис. 8).
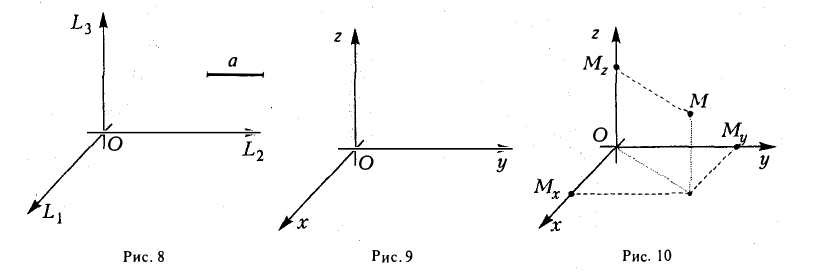
Назовем одну из этих осей осью абсцисс (осью Ох), вторую — осью ординат (осью Оу) и третью — осью аппликат (осью Oz) (рис. 9). Точка О называется началом координат. Пусть М — nроизвольная точка (рис. 10). Проведем через точку М nлоскости, перпендикулярные координатным осям, и поставим ей в соответстnие упорядоченную тройку чисел (х, у, z) по следующему правилу:
Числа х, у и z называются прямоугольными декартовыми координатами точки М; при этом х называется абсциссой точки М, у — ее ординатой, а z —аппликатой. Обозначение: М(х, у, z). Таким образом, в пространстве введена прямоугольная декартова система координат.
Оnределение:
Плоскость, проходящая через любую пару координатных осей, называется координатной плоскостью.
Координатных плоскостей три: Оху, Oyz и Oxz. Эти плоскости разбивают пространство на восемь частей — октантов. 1 .4. Простейшие задачи аналитической геометрии А. Расстояние между точками Пусть М 1 (х 1 ) и М 2 (х 2 )- две точки на координатной оси. Тогда расстояние d между ними вычисляется по формуле
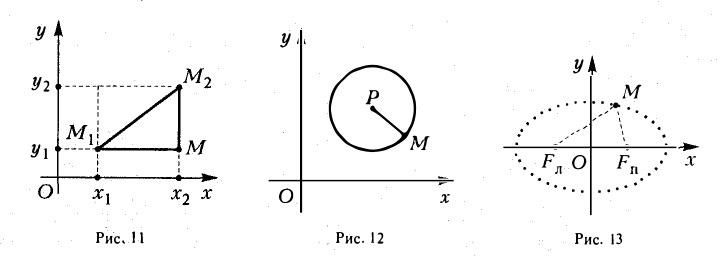
Если на плоскости задана прямоугольная декартова система координат Оху, то расстояние d между любыми двумя точками М 1 (х 1 , у1 и М2 (х2 , y2) вычисляется по следующей формуле
Рассмотрим прямоугольный треугольник ∆MM1M2 (pиc. l l). По теореме Пифагора
,и извлекая из обеих частей равенства квадратный корень, приходим к требуемой формуле .
Замечание:
Расстояние между точками 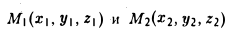
Задача:
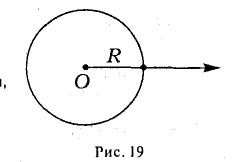
Написать уравнение окружности радиуса т с центром в точке Р(а, b).
Пусть М(х, у) — точка окружности (рис. 12). Это означает, что |M P| = r. Заменим |M P|его выражением
и возведем обе части полученного равенства в квадрат:
Это есть каноническое уравнение окружности радиуса r с центром в точке Р(а, b) .
Задача:
Пусть F л (-с, 0) и F n (c, 0) -фиксированные точки плоскости, а -заданное число (а > с ≥ 0). Найти условие, которому удовлетворяют координаты х и у точки М, обладающей следующим свойством: сумма расстояний от точки М до Fл и до F n равна 2а.
Вычислим расстояния между точками М и F л и между точками М и F n . Имеем
Перенесем второй корень в правую часть
Возводя обе части в квадрат, после простых преобразований получим
С целью дальнейших упрощений вновь возводим обе части в квадрат. В результате nриходим к равенству
Полагая b 2 = а 2 — с 2 и деля обе части nоследнего соотноwения на а 2 b 2 , nолучаем уравнение эллипса
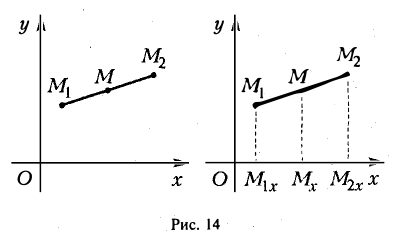
Деление отрезка в данном отношении:
Требуется выразить координаты х и у этой точки через координаты концов отрезка М1М2 и числа λ 1 и λ 2 . Предположим сначала, что отрезок М1М2 не параллелен оси ординат Оу (рис. 14). Тогда
то из последних двух соотношений получаем, что
Точка М лежит между точками М1 и М2 , поэтому либо х 1 х > х 2 . В любом из этих случаев разности х1 — х и х — х 2 имеют одинаковые знаки. Это позволяет переписать последнее равенство в следующей форме
В случае, когда отрезок М1М2 параллелен оси Оу, х 1 = х 2 = х. Заметим, что тот же результат дает формула (*), если nоложить в ней х 1 = х 2 . Справедливость формулы
доказывается аналогичным рассуждением .
Задача:
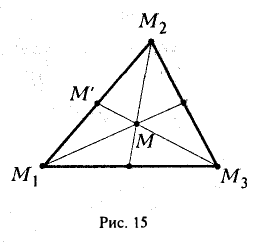
Найти координаты центра тяжести М треугольника с вершинами в точках . М1 ( х 1 , у 1 ), М2 ( х 2 , у 2 ) и М3 ( х 3 , у 3 ). Восnользуемся тем, что центр тяжести треугольника совпадает с точкой пересечения его медиан. Точка М делит каждую медиану в отношении 2 : 1, считая от вершины (рис. 15). Тем самым, ее координаты х и у можно найти по формулам
где х’ и у’ — координаты второго конца М’ медианы М3 М’. Так как М’ — середина отрезка М1М2, то
Полученные соотношения позволяют выразить координаты z и у центра тяжести М треугольника ∆М1М2М3 через координаты его вершин:
Замечание:
Полярные координаты
Предположим, что задана точка О, ось 
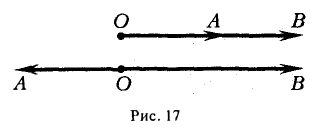
Пусть М — произвольная точка плоскости, отличная от точки О (рис.17). Ее положение на плоскости однозначно определяется двумя числами: расстоянием г между точками О и М и отсчитываемым против часовой стрелки углом φ между положительным лучом оси 
Точка О называется полюсом, 
Ясно, что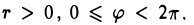
Таким образом, на плоскости можно задать еще одну координатную систему — полярную.
Прямоугольную декартову систему координат Оху будем называть согласованной с заданной полярной, если начало координат 0(0, 0) — полюс, ось Ох — полярная ось, а ось Оу составляете осью Ох угол, равный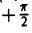
(рис.18). В свою очередь
Пример:
Пусть R > О — заданное число. Множество точек плоскости, полярные координаты (г,
Видео:Лекция 23. Виды уравнений прямой на плоскости.Скачать

Определители 2-го и 3-го порядков
Определителем второго порядка называется число
Обозначение:
Тем самым, для вычисления определителя второго порядка нужно из произведения а11, а22 элементов главной диагонали вычесть произведение а12, а21 элементов его побочной диагонали (рис. 20).
Пример:
По правилу (1) имеем
С определителями второго порядка мы встречаемся уже при отыскании решения системы двух линейных алгебраических уравнений с двумя неизвестными
Решая эту систему методом исключения неизвестных при условии, что
Пусгь теперь даны девять чисел aij (i = I, 2, 3; j = I, 2, 3).
Определителем третьего порядка называется число, обозначаемое символом
и вычисляемое по следующему правилу:
Первый индекс i элемента aij указывает номер строки, в которой он расположен, а второй индекс j — номер столбца.
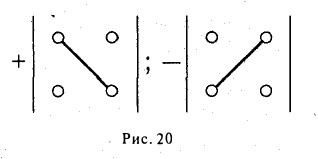
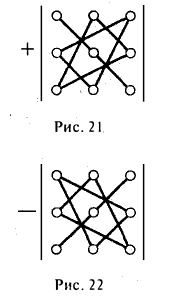
Чтобы разобраться с распределением знаков в правой части формулы (2), обратим внимание на следующее: произведение элементов а11, а22, а33 главной диагонали входит в формулу со своим знаком, также как и произведение а11, а22, а33 и а11, а22, а33 элементов, расположенных в вершинах треугольников, основания которых параллельны главной диагонали (рис. 21); с другой стороны, произведение а13, а22, а31 элементов побочной диагонали, а также произведения а12, а21, а33 и а11, а23, а32 — с противоположным знаком (рис.22). Такой подход к вычислению определителя третьего порядка называется правилом треугольника.
Пример:
Применяя правило треугольника, находим
Установим некоторые свойства определителей 3-го порядка, легко проверяемые при помощи разложений (1) и (2).
Свойство:
Величина определителя не изменится, если все его строки заменить его столбцами с теми же номерами
Свойство:
При перестановке любых двух строк (или любых двух столбцов) определителя он изменяет свой знак на противоположный.
Свойство:
Общий множитель всех элементов одной строки (или одного столбца) определителя можно вынести за знак определителя
Следующие три свойства определителя вытекают из свойств 1-3. Впрочем, в их справедливости можно убедиться и непосредственно, пользуясь формулами (1) и (2).
Свойство:
Если определитель имеет две равные строки (или дна равных столбца), то он равен нулю.
Свойство:
Если все элементы некоторой строки (или некоторого столбца) равны нулю, то и сам определитель равен нулю.
Свойство:
Если соответствующие элементы двух строк (или двух столбцов) пропорциональны, то определитель равен нулю.
Укажем еще один способ вычисления определителя 3-го порядка
Минором Mij элемента aij определителя ∆ называется определитель, получаемый изданного путем вычеркивания элементов i-й строки и j-ro столбца, на пересечении которых находится этот элемент. Например, минором элемента a23 будет определитель
Алгебраическим дополнением элемента Aij называется минор Mij — этого элемента, взятый со своим знаком, если сумма i + j номеров строки и столбца, на пересечении которых расположен элемент aij, есть число четное, и с противоположным знаком, если это число нечетное:
Теорема:
Определитель равен сумме произведений элементов любой его строки (любого его столбца) на их алгебраические дополнения, так что имеют место следующие равенства
Покажем, например, что
Пользуясь формулой (2), получаем, что
Правило (3) называется разложением определителя по элементам i-й строки, а правило (4) — разложением определителя по элементам j -го столбца.
Пример:
Раскладывая определитель по элементам 1-ой строки, получим
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Понятия связанного и свободного векторов
Рассмотрим две точки А и В. По соединяющему их отрезку можно перемещаться в любом из двух противоположных направлений. Если считать, например, точку А начальной, а точку В конечной, то тогда получаем направленный отрезок АВ, в другом случае — направленный отрезок В А. Направленные отрезки часто называют связанными или закрепленными векторами. На чертеже заданное направление указывается стрелкой (рис. 1).
В случае, когда начальная и конечная точки совпадают, А = В, связанный вектор называется нулевым.
Определение:
Будем говорить, что связанные векторы АВ и CD равны, если середины отрезков AD и ВС совпадают (рис. 2).
Обозначение:
Заметим, что в случае, когда точки А, В, С и D не лежат на одной прямой, это равносильно тому, что четырехугольник ABCD — параллелограмм. Ясно, что равные связанные векторы имеют равные длины.
Пример:
Рассмотрим квадрат и выберем векторы, как указано на рис.3. Векторы АВ и DC равны, а векторы ВС и DA не равны.
Укажем некоторые свойства равных связанных векторов:
- Каждый связанный вектор равен самому себе: АВ = АВ.
- Если АВ = CD, той CD = АВ.
- Если АВ = CD и CD = EF,то АВ = EF (рис.4).
Пусть АВ — заданный связанный вектор и С — произвольная точка. Ясно, что, опираясь на определение, всегда можно построить точку D так, чтобы
CD = АВ.
Тем самым, от каждой точки можно отложить связанный вектор, равный исходному (рис. 5).
Мы будем рассматривать свободные векторы, т. е. такие векторы, начальную точку которых можно выбирать произвольно, или, что то же самое, которые можно произвольно переносить параллельно самим себе. Ясно, что свободный вектор 
Если в качестве начальных выбирать лишь те точки, которые лежат на прямой, определяемой заданным (ненулевым) связанным вектором, то мы приходим к понятию скользящего вектора (рис. 6).
Связанные и скользящие векторы широко используются в теоретической механике.
Для обозначен ия свободных векторов будем пользоваться полужирными строчными латинскими буквами — а, b, с,… ; нулевой вектор обозначается через 0.
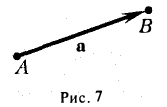
Пусть заданы вектор а и точка А. Существует ровно одна точка В, для которой

(рис.7). Операция построения связанного вектора АВ, для которого выполняется это равенство, называется откладыванием свободного вектора а от точки А.
Заметим, что связанные векторы, получаемые в результате описанной операции откладывания, равны между собой и, значит, имеют одинаковую дли ну. Это позволяет ввести длину свободного вектора а, которую мы будем обозначать символом |а. Длина нулевого вектора равна нулю. Если а = b, то |а| = |b; обратное неверно.
Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Линейные операции над векторами
Сложение векторов
Пусть заданы два вектора а и b. Возьмем какую-нибудь точку О и отложим от нее вектор a: 


Нетрудно заметить, что сложение векторов коммутативно, т. е. для любых векторов а и b справедливо равенство
а + b = b + а
Если отложить векторы а и 1» от обшей точки О и построить на них как на сторонах параллелограмм, то вектор 
Пусть заданы три вектора, например, a, b и с. Отложим от произвольной точки О вектор a: 

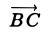

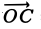
(а +b) + с = а + (b + с),
т. е. сложение векторов ассоциативно. Опуская скобки, можно говорить о сумме трех векторов и записывать ее так:
а + b + с.
Аналогично определяется сумма любого числа векторов: это есть вектор, который замыкает ломаную, построенную из заданных векторов. На рис. 14 показан», как построить сумму семи векторов:
Приведенный способ сложения произвольного числа векторов называется правилом замыкающего ломаную.
Пример:
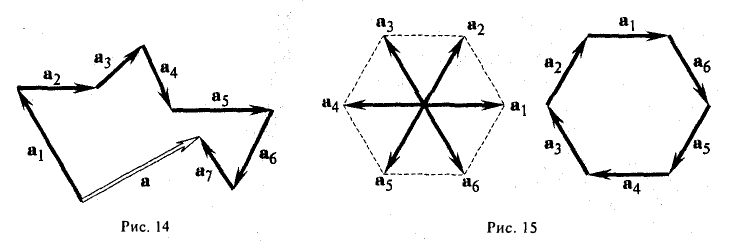
Найти сумму векторов, идущих из центра правильного шестиугольника в его вершины.
По правилу замыкающего ломаную получаем
Умножение вектора на число
Определение:
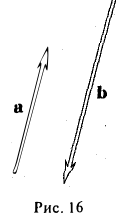
Свободные векторы а и b называются коллинеарными, если определяющие их связанные векторы лежат на параллельных или на совпадающих прямых (рис. 16).
Обозначение: а||b.
Замечание:
Из определения следует, что если хотя бы один из векторов a и b нулевой, то они коллинеарны.
Если отложить коллинеарные векторы а и b от обшей точки О, 

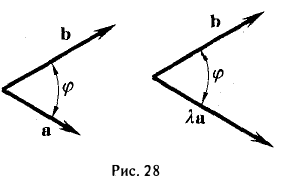
Если векторы имеют равные длины и одинаково направлены, то они равны. Пусть а — вектор, λ — вещественное число.
Определение:
Произведением вектора а на число λ называется вектор b такой, что
2) векторы а и b одинаково (соответственно, противоположно) направлены, если λ > 0 (соответственно, λ
(здесь λ и μ — любые действительные числа, а и Ь — произвольные векторы).
Определение:
Вектор, длина которого равна единице, называется единичным вектором, или ортом, и обозначается а° (читается: а с нуликом), |а°| = 1.
Если а ≠ 0, то вектор
есть единичный вектор (орт) направления вектора а (рис. 18).
Координаты и компоненты вектора
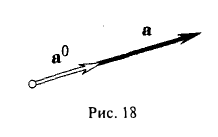
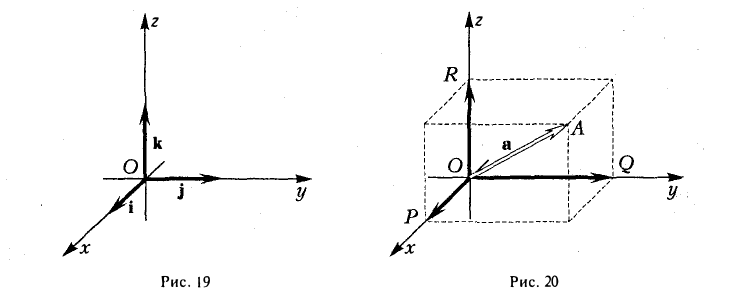
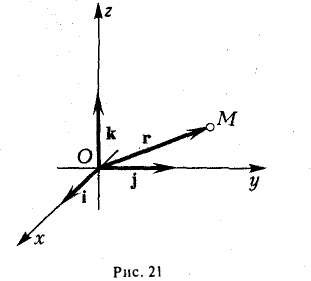
Выберем в пространстве прямоугольную декартову систему координат. Обозначим через i, j, к единичные векторы (орты) положительных направлений осей Ox, Оу, Oz (рис. 19). Рассмотрим произвольный вектор п, начало которого лежит в начале координат О, а конец — в точке А. Проведем через точку А плоскости, перпендикулярные осям Ох, Оу и Oz. Эти плоскости пересекут координатные оси в точках Р, Q и R соответственно. Из рис. 20 видно, что
Векторы 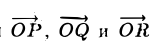
поэтому найдутся числа х, у, z такие, что
а = xi + yj + zk. (2)
Формула (2) называется разложением вектора а по векторам i, j, к. Указанным способом всякий вектор может быть разложен по векторам i, j, k.
Векторы i, j, к попарно ортогональны, и их длины равны единице. Тройку i, j, k называют ортонормированным (координатным) базисом (ортобазисом).
Можно показать, что для каждого вектора а разложение (2) по базису i, j, к единственно, т. е. коэффициенты х, у, z в разложении вектора а по векторам i, j, к определены однозначно. Эти коэффициенты называются координатами вектора а. Они совпадают с координатами х, у, z точки А — конца вектора а. Мы пишем в этом случае
а = .
Эта запись означает, что свободный вектор а однозначно задастся упорядоченной тройкой своих координат. Векторы xi, yj, zk, сумма которых равна вектору а, называются компонентами вектора а.
Из вышеизложенного следует, что два вектора а = < х1, у1, z1 > и b = <х2, у2, z2> равны тогда и только тогда, когда соответственно равны их координаты, т. е.
Радиус-вектором точки М(х,у, z) называется вектор г = xi + yj + zk, идущий из начала координат О в точку М (рис. 21).
Линейные операции над векторами в координатах
— при сложении векторов их координаты попарно складываются. Аналогично получаем
— при умножении вектора на число все его координаты умножаются на это число.
Пусть а = < х1, у1, z1>, b = < х2, у2, z2 > — коллинеарные векторы, причем b ≠ 0. Тогда а = μb, т.е.
Обратно, если выполняются соотношения (3), то а = μb, т. е. векторы a и b коллинеарны.
Таким образом, векторы а и b коллинеарны тогда и только тогда, когда их координаты пропорциональны.
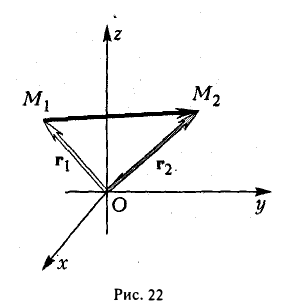
Пример:
Найти координаты вектора 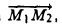
Из рис. 22 видно, что 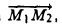
— координаты вектора ММг равны разностям одноименных координат конечной М2 и начальной М точек этого вектора.
Проекция вектора на ось
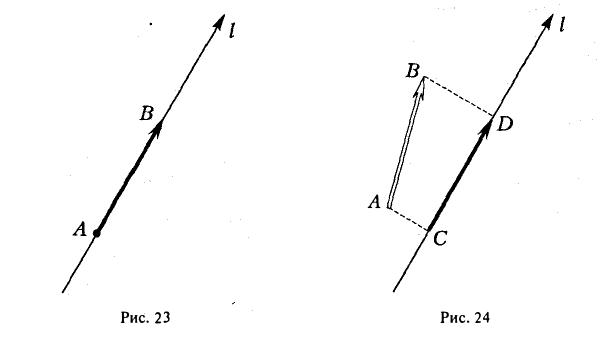
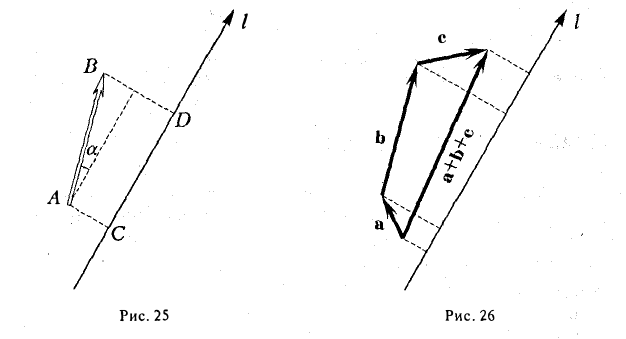
Рассмотрим на оси l ненулевой направленный отрезок АВ (рис.23). Величиной направленного отрезка АВ на оси l называется число, равное длине отрезка АВ, взятой со знаком «+», если направление отрезка АВ совпадаете направлением оси l, и со знаком «-», если эти направления противоположны.
Рассмотрим теперь произвольный вектор 
Определение:
Проекцией вектора 
Обозначение:
Основные свойства проекций
- Проекция вектора АВ на какую-либо ось l равна произведению длины вектора на косинус угла между осью и этим вектором (рис. 25)
- Проекция суммы векторов на какую-либо ось l равна сумме проекций векторов на ту же ось.
Видео:Геометрический смысл дифференциального уравненияСкачать

Скалярное произведение векторов
Пусть имеем два вектора a и b.
Определение:
Скалярным произведением вектора а на вектор b называется число, обозначаемое символом (а, b) и определяемое равенством
(1)
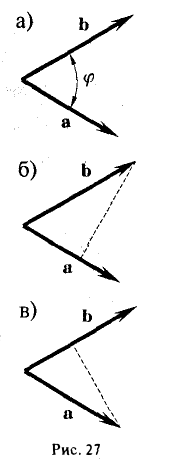
где φ, или в иной записи (
Заметив, что |b| cos φ есть проекция вектора b на направление вектора а, можем написать
(рис. 27 б) и, аналогично,’ (2)
(рис. 27 в), т.е. скалярное произведение двух векторов равно длине одного из них, помноженной на проекцию на него другого вектора. В случае, если один из векторов а или b — нулевой, будем считать, что
(a, b) = 0.
Свойства скалярного произведения
- Скалярное произведение обращается в нуль в том и только в том случае, когда по крайней мере один из перемножаемых векторов является нулевым или когда векторы а и b ортогональны, a ⊥ b.
Это следует из формулы (1), определяющей скалярное произведение.
Поскольку направление нулевого вектора не определено, мы можем его считать ортогональным любому вектору. Поэтому указанное свойство скалярного произведения можно сформулировать так:
2. Скалярное произведение коммутативно:
(а, b) = (b, а).
Справедливость утверждения вытекает из формулы (I), если учесть четность функции cos φ: cos(- φ) = cos φ.
3. Скалярное произведение обладает распределительным свойством относительно сложения:
(а + b, с) = (а, с) + (b, c).
4. Числовой множитель А можно выносить за знак скалярного произведения
(λа, b) = (а, λb) = λ (а, b).
- Действительно, пусть λ > 0. Тогда
поскольку при λ > 0 углы (

Аналогично рассматривается случай λ
Замечание:
В общeм случае (а, b)c ≠ a(b, c).
Скалярное произведение векторов, заданных координатами
Пусть векторы а и b заданы своими координатами в ортонормированном базисе i, j, k:
Рассмотрим скалярное произведение векторов а и b:
Пользуясь распределительным свойством скалярного произведения, находим
То есть, если векторы а и b заданы своими координатами в ортонормированном базисе, то их скалярное произведение равно сумме произведений одноименных координат.
Пример:
Найти скалярное произведение векторов n = 4i — 2j + k и b = 6i + 3j + 2k.
(a, b) = 4 • 6 + (-2) • 3 + 1 • 2 = 20.
Скалярное произведение вектора на себя называется скалярным квадратом:
(а, а) = а 2 .
Применяя формулу (4) при b = а, найдем (5)
С другой стороны,
так что из (5) следует, что (6)
— в ортонормированном базисе длина вектора равна квадратному корню из суммы квадратов его координат.
Косинус угла между векторами. Направляющие косинусы
Согласно определению
(а, b) = |а| • |b| • cos φ,
где φ — у гол между векторами а и b. Из этой формулы получаем
(7)
(предполагается, что векторы а и b — ненулевые).
Пример:
Найти угол между векторами a = и d = . Пользуясь формулой (8), находим
или, в координатной записи, (9)
где а есть угол, образованный вектором я с осью Ох. Аналогично получаем формулы
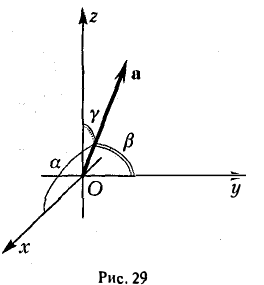
Формулы (9)-(11) определяют направляющие косинусы вектора а, т. е. косинусы углов, образуемых вектором n с осями координат (рис. 29).
Пример:
Найти координаты единичного вектора n°. По условию | n°| = 1. Пусть n° = zi+ yj+ zk. Тогда
Таким образом, координатами единичного вектора являются косинусы углов, образованных этим вектором с осями координат:
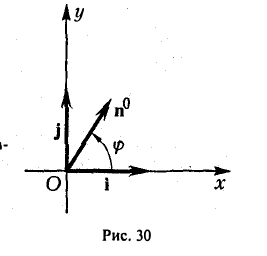
Пример:
Пусть единичный вектор n° ортогонален оси z:
(рис. 30). Тогда его координаты г и у соответственно равны
x=cos φ, y = sin φ.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Векторное произведение векторов
Определение:
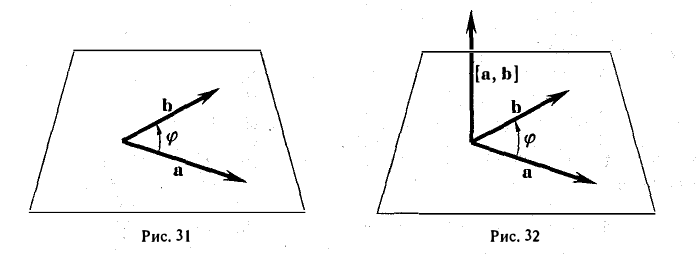
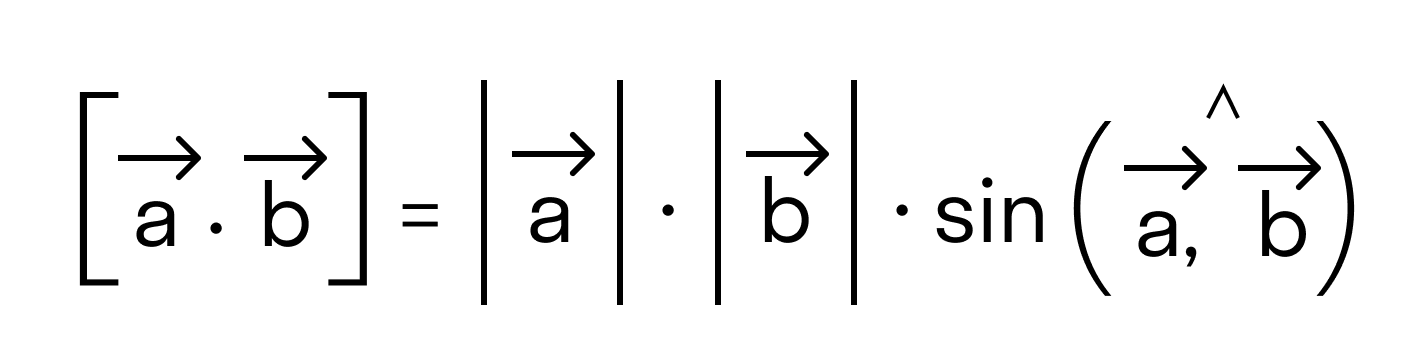
Векторным произведением вектора а на вектор b называется вектор, обозначаемый символом [a, b] (или a х b), такой, что
1) длина вектора [а, b] равна |а| • |Ь| • sin φ, где φ — угол между векторами а и b (рис.31);
2) вектор [а, b] перпендикулярен векторам а и b, т.е. перпендикулярен плоскости этих векторов;
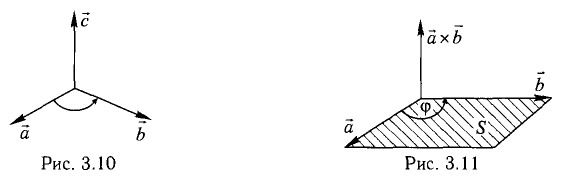
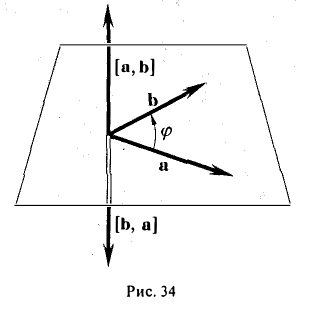
3) вектор [а, Ь] направлен так, что из конца этого вектора кратчайший поворот от л к Ь виден происходящим против часовой стрелки (рис. 32).
Иными словами, векторы я, b и [a, b] образуют правую тройку векторов, т.е. расположены так, как большой, указательный и средний пальцы правой руки. В случае, если векторы a и b коллинеарны, будем считать, что [a, b] = 0.
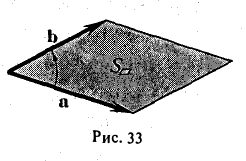
По определению длина векторного произведения (1)
численно равна площади 
|[a, b]| = 
Свойства векторного произведения
- Векторное произведение равно нулевому вектору тогда и только тогда, когда по крайней мере один из перемножаемых векторов является нулевым или когда эти векторы коллинеарны (если векторы я и b коллинеарны, то угол между ними равен либо 0, либо тг).
Это легко получить из того, что |[a, b]| = |a| • |b| • sin φ.
Если считать нулевой вектор коллинеарным любому вектору, то условие коллинеарности векторов a и b можно выразить так
2. Векторное произведение антикоммутативно, т. е. всегда (2)
В самом деле, векторы [а, b] и [b, а] имеют одинаковую длину и коллинеарны. Направления же этих векторов противоположны, так как из конца вектора [a, b] кратчайший поворот от a к b будет виден происходящим против часовой стрелки, а из конца вектора [b, a] — почасовой стрелке (рис. 34).
3. Векторное произведение обладает распределительным свойством по отношению к сложению
4. Числовой множитель λ можно выносить за знак векторного произведения
Векторное произведение векторов, заданных координатами
Пусть векторы a и b заданы своими координатами в базисе i,j, k: а = < х1, у1, z1>, b = < х2, у2, z2 >. Пользуясь распределительным свойством векторного произведения, находим (3)
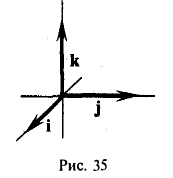
Выпишем векторные произведения координатных ортов (рис. 35):
Поэтому для векторного произведения векторов a и b получаем из формулы (3) следующее выражение (4)
Формулу (4) можно записать в символической, легко запоминающейся форме, если воспользоваться определителем 3-го порядка: (5)
Разлагая этот определитель по элементам 1-й строки, получим (4). Примеры:
- Найти площадь параллелограмма, построенного на векторах а = i + j- k, b = 2i + j- k.
Искомая площадь 
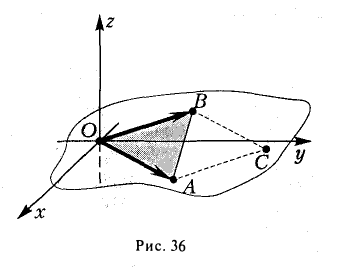
2. Найти площадь треугольника ОАВ (рис.36).
Ясно, что площадь S∆ треугольника ОАВ равна половине площади S параллелограмма О АС В. Вычисляя векторное произведение [a, b] векторов a= 

Замечание:
Векторное произведение не ассоциативно, т.е. равенство [[а, b], с] = [а, b,с]] в общем случае неверно. Например, при а = i, b = j. c= j имеем
Видео:Аналитическая геометрия, 3 урок, Векторное произведениеСкачать

Смешанное произведение векторов
Пусть имеем три вектора а, b и с. Перемножим векторы а и b векторно. В результате получим вектор [а, b). Умножим его скалярно на вектор с:
([a, b], с).
Число ([а, b], с) называется смешанным произведением векторов а, b, с и обозначается символом (а, b, с).
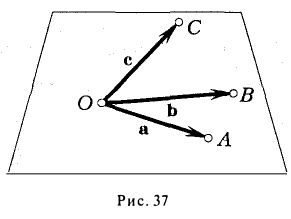
Геометрический смысл смешанного произведения
Отложим векторы а, b и с от общей точки О (рис. 37). Если все четыре точки О, А, В, С лежат в одной плоскости (векторы a, b и с называются в этом случае компланарными), то смешанное произведение ([а, b], с) = 0. Это следует из того, что вектор [а, b] перпендикулярен плоскости, в которой лежат векторы а и b, а значит, и вектору с.
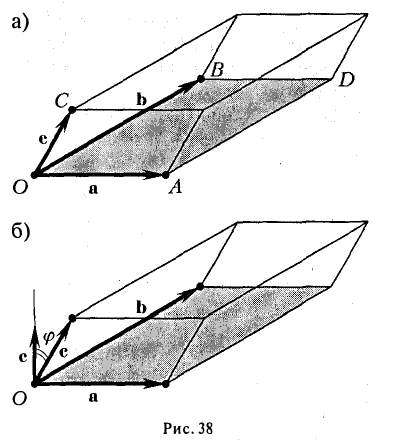
Если же точки О, А, В, С не лежат в одной плоскости (векторы a, b и с некомпланарны), построим на ребрах OA, OB и ОС параллелепипед (рис. 38 а). По определению векторного произведения имеем
где 
Умножая обе части последнего равенства справа скалярно на вектор с, получаем, что
Число ргe с равно высоте h построенного параллелепипеда, взятого со знаком « + », если угол ip между векторами с и с острый (тройка а, b, с — правая), и со знаком «-», если угол — тупой (тройка а, b, с — левая), так что
Тем самым, смешанное произведение векторов a, b и с равно объему V параллелепипеда, построенного на этих векторах как на ребрах, если тройка а, b, с — правая, и -V, если тройка а, b, с — левая.
Исходя из геометрического смысла смешанного произведения, можно заключить, что, перемножая те же векторы a, b и с в любом другом порядке, мы всегда будем О получать либо +V, либо -V. Знак произведения будет зависеть лишь от того, какую тройку образуют перемножаемые векторы — правую или левую. Если векторы а, b, с образуют правую тройку, то правыми будут также тройки b, с, а и с, а, b. В то же время все три тройки b, а, с; а, с, b и с, b, а — левые. Тем самым,
(а, b, с) = (b, с, а) = (с, a,b) = -(b, а, с) = -(а, с, b) = -(с, b, а).
Еще раз подчеркнем, что смешанное произведение векторов равно нулю тогда и только тогда, когда перемножаемые векторы а, b, с компланарны:
Смешанное произведение в координатах
Пусть векторы а, b, с заданы своими координатами в базисе i, j, k:
Найдем выражение для их смешанного произведения (а, b, с). Имеем
— смешанное произведение векторов, заданных своими координатами в базисе i, j, k, равно определителю третьего порядка, строки которого составлены соответственно из координат первого, второго и третьего из перемножаемых векторов.
Пример:
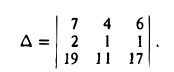
Проверить, компланарны ли векторы
Рассматриваемые векторы будут компланарны или некомпланарны в зависимости от того, будет равен нулю или нет определитель
Разлагая его по элементам первой строки, получим
Двойное векторное произведение
Двойное векторное произведение [а, [b, с]] представляет собой вектор, перпендикулярный к векторам а и [b, с]. Поэтому он лежит в плоскости векторов b и с и может быть разложен по этим векторам. Можно показать, что справедлива формула
[а, [b, с]] = b(а, с) — с(а, b).
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Математика это не ИсламСкачать

Векторное произведение векторов
О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Видео:18+ Математика без Ху!ни. Векторное произведение.Скачать

Определение векторного произведения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.
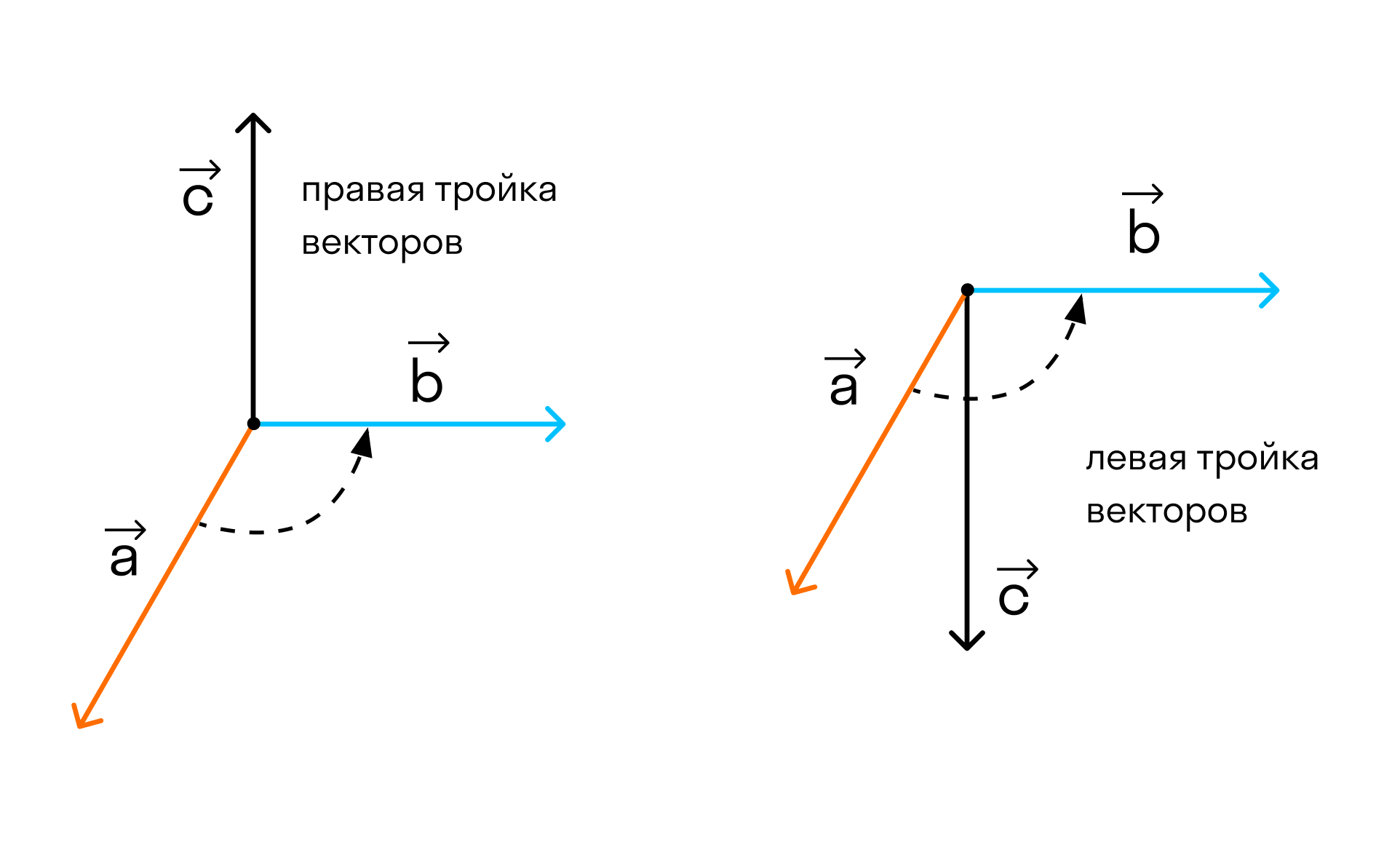
Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.
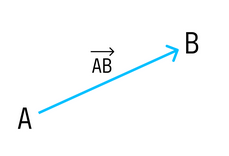
Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.
Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.
Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.
Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.
В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.
И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.
Еще не устали от теории? Онлайн-школа Skysmart предлагает обучение на курсах по математике — много практики и поддержка внимательных преподавателей!
Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:
- он является нулевым, если векторы →a и →b коллинеарны;
- он перпендикулярен и вектору →a и вектору →b;
- длина векторного произведения равна произведению длин векторов →a и →b на синус угла между ними
- тройка векторов →a, →b, →c ориентирована так же, как и заданная система координат.
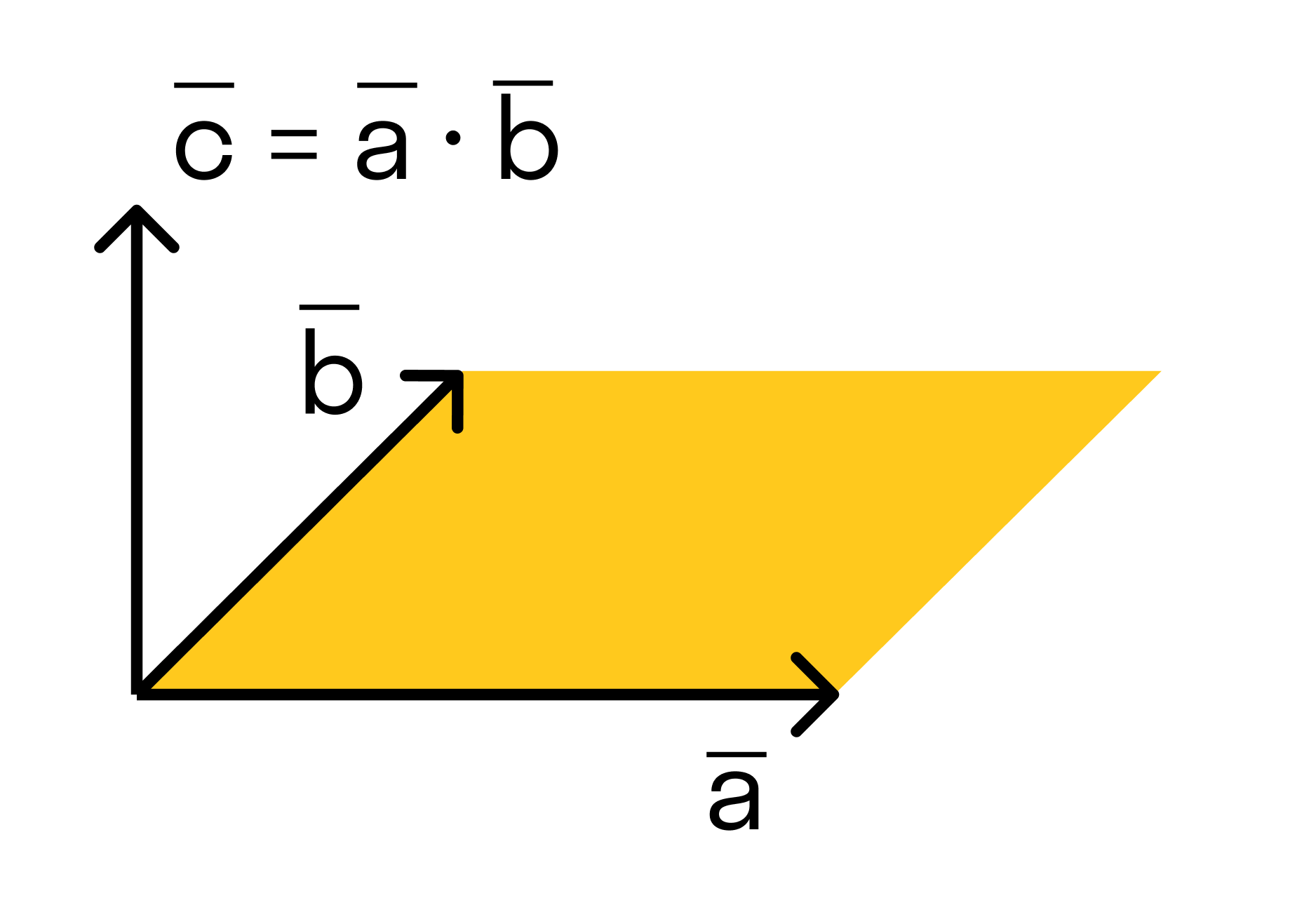
Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.
Векторное произведение двух векторов a = и b = в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов:
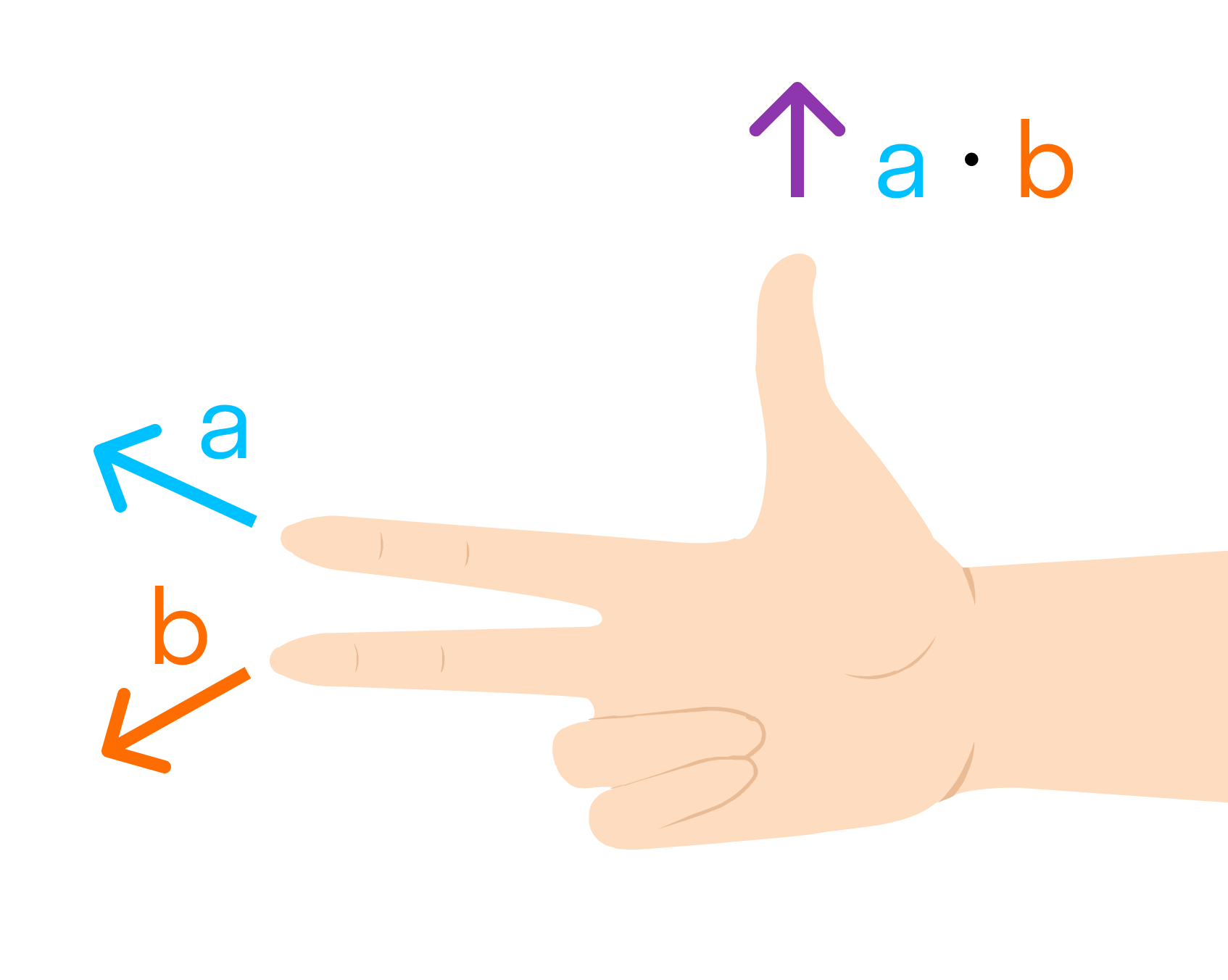
Векторное произведение векторов →a и →b обозначается как [→a • →b].
Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.
Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.
Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:
- Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
- Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
- Если определитель равен нулю, то векторы компланарны (линейно зависимы).
Видео:Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

Координаты векторного произведения
Рассмотрим векторное произведение векторов в координатах.
Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.
В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор
→i, →j, →k — координатные векторы.
Это определение показывает нам векторное произведение в координатной форме.
Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:
Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:
Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.
Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Свойства векторного произведения
Векторное произведение в координатах представляется в виде определителя матрицы:
На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:
- Антикоммутативность
- Свойство дистрибутивности
Сочетательное свойство
, где λ произвольное действительное число.
Для большей ясности докажем свойство антикоммутативности векторного произведения.
Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому
что доказывает свойство антикоммутативности векторного произведения.
Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.
Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).
Видео:Математика без Ху!ни. Свойства скалярного и векторного произведений.Скачать

Примеры решения задач
Пример 1
а) Найти длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
б) Найти площадь параллелограмма, построенного на векторах →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
а) По условию требуется найти длину векторного произведения. Подставляем данные в формулу:
Так как в задаче речь идет о длине, то в ответе указываем размерность — единицы.
б) По условию требуется найти площадь параллелограмма, который построен на векторах →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:
Пример 2
Найти |[-3→a x 2→b]|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.
По условию снова нужно найти длину векторного произведения. Используем нашу формулу:
Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
Выносим константу за пределы модуля, при этом модуль позволяет убрать знак минус. Длина же не может быть отрицательной.
Пример 3
Даны вершины треугольника A (0, 2, 0), B (-2, 5,0), C (-2, 2, 6). Найти его площадь.
Сначала найдём векторы:
Затем векторное произведение:
Вычислим его длину:
Подставим данные в формулы площадей параллелограмма и треугольника:
Видео:Геометрический смысл скалярного произведения. ТемаСкачать

Геометрический смысл векторного произведения
По определению длина векторного произведения векторов равна
А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.
Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.
Видео:Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Физический смысл векторного произведения
В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.
Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F].
Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.
Видео:11. Прямая в пространстве и ее уравненияСкачать

Векторный метод в курсе геометрии основной школы
ВЕКТОРНЫЙ МЕТОД В КУРСЕ ГЕОМЕТРИИ ОСНОВНОЙ ШКОЛЫ
Традиционно одной из самых сложных тем школьного курса геометрии является тема “Применение векторов к решению задач”. В то же время понятие вектора является одним из фундаментальных понятий современной математики, а векторный метод является одним из широко употребляемых, красивых и современных методов решения задач.
Вектор – одно из фундаментальных понятий современной математики и широко используется в различных её областях. В работах Г. Бесселя, Ж. Аргана и К. Гаусса по теории комплексных чисел установлена связь между арифметическими операциями над векторами в двумерном пространстве. В работах В. Гамильтона, Г. Грассмана, Ф. Мёбиуса понятие вектора нашло широкое применение при изучении свойств трёхмерного пространства. В настоящее время на векторной основе излагаются линейная алгебра, аналитическая и дифференциальная геометрия, функциональный анализ.
К понятию вектора как направленного отрезка приводят многие задачи механики и других областей физики: теории упругости, теории электромагнитных полей.
Векторный аппарат используется при доказательстве некоторых теорем и решении многих задач. Сила векторного метода заключается в том, что он позволяет легко делать обобщения, роль которых в математике трудно переоценить
Цели изучения векторного метода в средней школе:
§ дать эффективный метод решения различных геометрических задач (как аффинных, так и метрических) и доказательства теорем;
§ показать широкое применение векторного аппарата в других областях знаний: технике, физике, химии, лингвистике – и на базе этого расширять их кругозор и формировать мировозрение;
§ использовать векторный метод при решении задач с целью форматирования у учащихся выполнять обобщение и конкретизацию;
§ формировать у учащихся такие качества мышления, как гибкость (нешаблонность), целенаправленность, рациональность, критичность и др.
В своей статье я рассматриваю векторы в школьном курсе геометрии на основе учебника геометрии для общеобразовательных учреждений следующего коллектива авторов: , , и др.
Понятие вектора и действия над векторами вводятся в 9 классе( в 8 классе – 2-ой вариант программы), так, как это принято в физике. Величины, которые характеризуются не только числовым значением, но и направлением, называются в физике векторными и изображаются отрезками со стрелкой. Поэтому геометрический вектор вводится как направленный отрезок, т. е. отрезок на котором дано направление от одного конца к другому.
На изучение главы «Векторы», в которой рассматриваются 3 учебные темы, отводится 8 часов(12 часов – 2 вариант программы).
Основная цель изучения темы «Векторы» в 8-9 классах — научить обучающихся выполнять действия над векторами как направленными отрезками, что важно для применения векторов в физике; познакомить с использованием векторов при решении геометрических задач.
Основное внимание уделяется выработке умений выполнять операции над векторами (складывать векторы по правилам треугольника и параллелограмма, строить вектор, равный разности двух данных векторов, а также вектор, равный произведению данного вектора на данное число):
На примерах показывается, как векторы могут применяться к решению геометрических задач.
В результате изучения данной главы в основной школе учащиеся приобретают следующие знания и умения, соответствующие требованиям стандарта основного общего образования (Таблица 1).
Требования стандарта образования
· Понятия вектора, его начала и конца, нулевого вектора, длины вектора, коллинеарных, сонаправленных, противоположно направленных и равных векторов
· Изображать и обозначать векторы
· откладывать от данной точки вектор, равный данному
· решать типовые задачи
Сложение и вычитание векторов
· определение суммы двух векторов
· законы сложения векторов (правило треугольника и параллелограмма)
· понятие суммы трёх и более векторов
· определение разности двух векторов
· какой вектор называется противоположным данному
· объяснить, как определяется сумма двух или более векторов
· строить сумму двух или более данных векторов, пользуясь правилами треугольника, параллелограмма, многоугольника
· строить вектор, равный разности двух векторов
· решать типовые задачи
Умножение вектора на число. Применение векторов к решению задач
· понятие умножения вектора на число
· свойства умножения вектора на число
· понятие средней линией трапеции и её свойства
· формулировать свойства умножения вектора на число
· формулировать и доказывать теорему о средней линии трапеции
· применять векторы к решению задач
Для решения задач учащиеся должны владеть следующими умениями, которые и являются компонентами векторного метода:
1) перевод условия задачи на язык векторов, в том числе:
§ введение в рассмотрение векторов;
§ выбор базисных векторов;
§ разложение всех введенных векторов
2) составление системы векторных равенств (или одного равенства).
3) упрощение векторных равенств
4) замена векторных равенств алгебраическими уравнениями и их решения
5) объяснение геометрического смысла полученного решения этой системы (или одного уравнения).
Понятийный аппарат и умения, которыми должен овладеть ученик, чтобы научиться решать геометрические задачи векторным методом в основной школе:
§ основные понятия: вектор, начало вектора, конец вектора, одинаково направленные векторы, противоположно направленные векторы, абсолютная величина вектора (модуль вектора), равные векторы, нулевой вектор, неколлинеарные векторы;
§ 
§ действия для овладения компонентами метода: перевод геометрических терминов на язык векторов и решение обратной задачи; перевод условия задачи на язык векторов, т. е. составление системы векторных равенств по условию задачи; выбор базисных векторов, разложение всех введенных в рассмотрение векторов по базисным векторам; упрощение системы векторных равенств; замена векторных равенств алгебраическими.
С целью систематизации и обобщения знаний учащихся по теме «Векторы», для повторения основных понятий темы уместно использовать опорные таблицы (Рисунок 2).
В курсе геометрии основной школы выделяется три типа задач, которые целесообразно решать с помощью векторов.
Первый тип: задачи, связанные с доказательством параллельности прямых и отрезков
Второй тип: задачи, в которых доказывается, что некоторая точка делит отрезок в заданном отношении.
Третий тип: задачи на доказательство принадлежности трех и более точек одной прямой.
Выделение таких типов полезно по следующим соображениям:
1. Эти виды наиболее многочисленны и, в силу простого перевода на векторный язык, могут служить образцами для учащихся.
2. Навык, приобретенный при решении этих задач, можно переносить на более сложные (где данные задачи могут встречаться в виде части задач).
Указанные выше типы задач охватывают довольно большую часть тех задач, которые приходиться решать учащимся. В задачах такого рода традиционные методы решения связаны обычно со значительными трудностями: или с необходимостью тонких дополнительных геометрических построений, или с довольно громоздкими тригонометрическими преобразованиями.
Решение геометрических задач векторным методом позволяет отработать у учащихся навыки перевода условия с геометрического языка на векторный и формировать навыки, необходимые для перевода с векторного языка на геометрический.
Для овладения умением переходить от геометрического языка к векторному и обратно необходимо знать, как то или иное векторное соотношение выражается на геометрическом языке. (Таблица 3)
Рисунок
Что необходимо доказать или определить на геометрическом языке.
Что достаточно определить или доказать на векторном языке.

( 
C

C






C 

Многообразие возможностей применения векторного аппарата и его роль в повышении и развитии математической культуры учащихся трудно переоценить. Векторное решение задач аффинной геометрии зачастую проще их решения средствами элементарной геометрии. При этом можно обойтись без тех дополнительных построений, которые иногда затрудняют поиск решения задачи.
1. Атанасян геометрии в 7-9 классах. Пособие для учителей/, , и др.. — 7-е изд. — М., Издательство «Просвещение», 2009,. -255 с.
2. Геометрия.7-11 класс [Электронный ресурс].-Демонстрационные таблицы(258 Мб).-Волгоград: Издательство «Учитель», 2011-1 электрон. опт. диск (CD — ROM)
3. Кушнир методы решения задач/ . — Киев: Издательство «Обериг», 1994 – 207с.
🎬 Видео
Физика | Ликбез по векторамСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

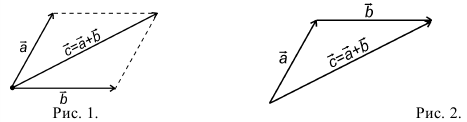
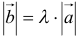 ;
;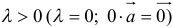 .
.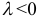 .
.