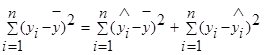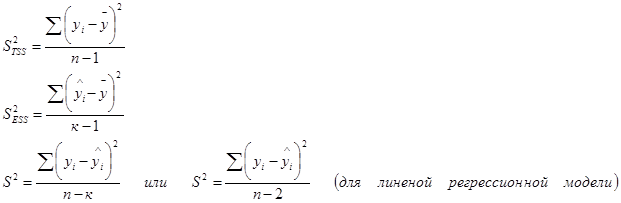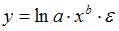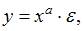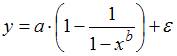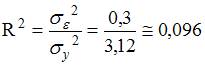Цель регрессионного анализа состоит в том, чтобы объяснить поведение переменной Ув зависимости от изменения выбранных факторов X1, Х2,…, Хn. В парном регрессионном анализе мы пытаемся объяснить поведение Упутем определения регрессионной зависимости У от фактораX. Для этой цели используется метод дисперсионного анализа.
Замечание: В математической статистике дисперсионный анализ рассматривается как самостоятельный метод статистического анализа. Мы же будем применять его как вспомогательное средство для изучения качества регрессионной модели.
Согласно основной идеи дисперсионного анализа общую сумму квадратов отклонений переменной у от среднего значения ӯ можно разложить на 2 части: объясненную и необъясненную:
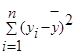
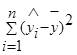
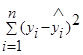
— общая сумма квадратов отклонений (TSS ),
— объясненная или регрессионная сумма квадратов (ESS ),
— необъясненная или остаточная сумма квадратов (RSS ).
Общая сумма квадратов отклонений значения результативного показателя от среднего значения вызвано множеством причин. Условно разделим всю совокупность на 2 группы: влияние изучаемого фактораX и влияние прочих факторов. Если фактор X не влияет наУ, то линия регрессии параллельна оси ОХ (ŷ=ӯ), тогда вся дисперсия результативного показателя обусловлена воздействием прочих факторов. TSS= RSS.
Если же прочие факторы не влияют на результат, тоУ связан с X функционально и остаточная сумма квадратов отклонений отсутствует. TSS=ESS.
Поскольку не все точки корреляционного поля лежат на линии регрессии, то всегда имеется их разброс, обусловленный влиянием как фактора X, так и воздействием прочих причин. Пригодность линии регрессии для прогноза зависит от того какая часть общего отклонения показывается У приходится на объясненную часть. Очевидно, что если ESS>RSS, то уравнение регрессии статистически значимо и фактор X оказывает существенное влияние на результативный показательУ.
Любая сумма квадратов отклонений связана с числом степеней свободы. Число степеней свободы fзависит от объема выборки n и от числа определенных по этой выборке параметров к (для линейной модели к=2, т.к. ŷ =а+bх) можно показать, что для общей TSS число степеней свободы f1=n-1, для объясненной ESS — f2=к-1, для необъясненной RSS – f3=n-к.
Разделив по членено каждое слагаемое равенства (4.1) на соответствующую ей степень свободы, получим средний квадрат отклонений или дисперсию на одну степень свободы.
и 
является несмещенными оценками дисперсии результирующего показателя обусловленных соответственно объясненной переменной х и под воздействием неучтенных случайных факторов.
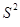
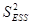
Определение дисперсии на одну степень свободы приводит их к сравнимому виду и это используется в дальнейшем для проверки значимости влияния фактора х на результирующий показатель. (проверка фактора регрессии): для этого определяют:
(4.2)
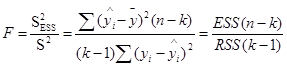
Величина F называется F-критерием (отношение) Фишера.
Проверка статистических гипотез.
Статистической гипотезой H называется предположение относительно параметров или виды распределения случайной величины.
Нулевой (основной) называют выдвинутую гипотезу H0, альтернативной гипотезе H1, которая противоречит основной.
Проверку статистической гипотезы выполняют на основе результатов выборки. Поскольку выборка имеет ограниченный объем, то применяется возможность того, что будет отвергнута правильная нулевая гипотеза называемая уровнем значимости.
a = 5% (0,05) – это означает, что в 5 случаях из 100 верная гипотеза будет отвергнута.
Статистическим критерием (F или t) называется случайная величина, которая служит для проверки нулевой гипотезы. В качестве статистического критерия выбирается такая случайная величина точная или приближенная распределение, которой известно.
Наблюдаемым значением (Fнабл или tнабл) называется значение критерия вычисленного по данным выборки.
Множество значений критерия разбивают на 2 непересекающихся области: критическая и область принятия решений.
Критической областью называется совокупность значений критерии, при которой гипотеза H0 отвергается.
Область принятия решений – это совокупность значений критерия, при которых гипотеза H0 принимается.
Критическими точками называются точки отделяющие критическую область от области принятия решений, и обозначается (Fкр, tкр).
Критические точки определяются по таблицам известного распределения выборочного критерия при заданном уровне значимости a и числе степеней свободы f.
Сравнивая наблюдаемые значения критерия с критическими точками можно принять или отвергнуть нулевую гипотезу.
Пусть нулевая гипотеза состоит в том, что утверждается отсутствие связи между переменными.
Английский статистик Снедекор разработал статистические таблицы значений F – критерия при различных уровнях значимости a и различных степенях свободы f2 и f3.
если Fрас>Fтаб, то H0 отклоняется связь между Х и У существенна;
если Fрас tкр, то H0 отклоняется, т.е. коэффициент данный значим.
Замечание: В эконометрических исследования проверку гипотез осуществляют при 5% и 1% уровне значимости.
Если H0 отклоняется при 1% уровне значимости, то она автоматически отклоняется и при 5% уровне; если H0 принимается при 5% уровне, то она принимается и при 1% уровне; если при 5% уровне гипотезы отклоняются, а при 1% принимается, то результаты проверки гипотез проводятся при обеих уровнях значимости.
В ряде прикладных задач требуется оценить значимость коэффициента корреляции r; для этого проверяется H0 о равенстве нулю теоретического коэффициента корреляции ρ=0. При этом исходят из того, что при отсутствии корреляционной связи статистика: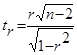 
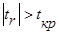
(5.2) имеет t-распределение Стьюдента с n-2 степенями свободы. Коэффициента корреляции r значим на уровне a, если 
, где tкр – это табличное значение t-критерия при уровне значимости a и числе степеней свободы f=n-2.
§ 1.2. Коэффициент корреляции.
Для оценки тесноты корреляционной зависимости используют выборочный коэффициент корреляции r или r(х,у).
где 
В этом уравнении (2.1) величина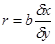 
показывает насколько величин dу изменится в среднем у, когда х увеличится dх. Величина r является показателем тесноты линейной связи между х и уи называется выборочным коэффициентом корреляции.
 |
 |
У
 |
| |
 |
 |
 |
 |
Если r>0 (b>0), то корреляционная связь между переменными называются прямой, т.е. при увеличении значения переменной Х увеличивается значение условной средней переменной У.
| | | следующая лекция ==> | |
| Ценообразование на рынке земли | | | Понятие и история формирования экономики общественного сектора |
Дата добавления: 2016-01-16 ; просмотров: 6689 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Множественная степенная регрессияСкачать
Тема 10: Оценка качества подбора уравнения
1. Известно, что доля остаточной регрессии в общей составила 0,19. Тогда значение коэффициента корреляции равно …
Решение:
Известно, что доля остаточной регрессии в общей составила 0,19. Значит, 
Найдем коэффициент детерминации: 
Вычислим коэффициент корреляции: 
2. Известно, что общая сумма квадратов отклонений 
, а остаточная сумма квадратов отклонений, 
. Тогда значение коэффициента детерминации равно …
Решение:
Для расчета коэффициента детерминации можно пользоваться следующей формулой: 
. Значит, в нашем случае коэффициент детерминации равен: 
3. Для регрессионной модели вида 
, где 
рассчитаны дисперсии: 
; 
; 
. Тогда величина 
характеризует долю …
Решение:
Значение коэффициента детерминации 
характеризует долю дисперсии зависимой переменной, объясненную построенным уравнением регрессии, в общей дисперсии зависимой переменной. Разность 
характеризует долю остаточной дисперсии, которая может быть рассчитана также по формуле . Поэтому отношение характеризует долю остаточной дисперсии.
4. Если общая сумма квадратов отклонений 
, и остаточная сумма квадратов отклонений , то сумма квадратов отклонений, объясненная регрессией, равна …
Решение:
Общая сумма квадратов отклонений складывается из суммы квадратов отклонений, объясненных регрессией, и остаточной сумма квадратов отклонений.
Значит, сумма квадратов отклонений, объясненная регрессией, равна разности общей сумме квадратов отклонений и остаточной суммы квадратов отклонений.
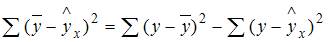
Получается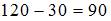 
.
Тема 11: Проверка статистической значимости эконометрической модели
1. При расчете скорректированного коэффициента множественной детерминации пользуются формулой 
, где …
n – число наблюдений; m – число факторов, включенных в модель множественной регрессии
m – число наблюдений; n – число факторов, включенных в модель множественной регрессии
n – число параметров при независимых переменных; m – число факторов, включенных в модель множественной регрессии
n – число параметров при независимых переменных; m – число наблюдений
Решение:
Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и имеет вид , где n – число наблюдений, m – число факторов, включенных в модель множественной регрессии.
2. Если известно уравнение множественной регрессии 
построенное по результатам 50 наблюдений, для которого общая сумма квадратов отклонений равна 153, и остаточная сумма квадратов отклонений равна 3, то значение F-статистики равно …
Решение:
Расчет F-статистики начинается с разложения общей суммы квадратов отклонений на сумму квадратов отклонений, объясненную регрессией, и остаточную сумму квадратов отклонений:
, где
– общая сумма квадратов отклонений
– сумма квадратов отклонений, объясненная регрессией
– остаточная сумма квадратов отклонений
В нашем случае дано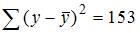 
, 
. Следовательно, 
Существует равенство между числом степеней свободы общей, факторной и остаточной сумм квадратов отклонений:
n – 1 = m + (n – m – 1), где n –число наблюдений, m – число параметров перед переменными в уравнений регрессии.
Число степеней свободы для общей суммы квадратов отклонений равно n – 1. В нашем случае n – 1 = 49.
Число степеней свободы для остаточной суммы квадратов отклонений равно n – m – 1 = 46.
Число степеней свободы для факторной суммы квадратов отклонений равно m = 3.
Рассчитаем факторную и остаточную дисперсии на одну степень свободы по формулам 
F-статистика вычисляется по формуле 
3. Для регрессионной модели известны следующие величины дисперсий:
где y – значение зависимой переменной по исходным данным; 
– значение зависимой переменной, вычисленное по регрессионной модели; 
– среднее значение зависимой переменной, определенное по исходным статистическим данным. Для указанных дисперсий справедливо равенство …
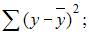
Решение:
Назовем приведенные дисперсии: 
– общая дисперсия; 
– объясненная дисперсия; 
– остаточная дисперсия. При анализе статистической модели величину общей дисперсии рассматривают как сумму объясненной и остаточной дисперсий, поэтому справедливо равенство: 
Тема 12: Оценка значимости параметров эконометрической модели
1. Для уравнения множественной регрессии вида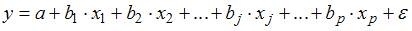 
на основании 14 наблюдений рассчитаны оценки параметров и записана модель: 
(в скобках указаны значения t-статистики, соответствующие параметрам регрессии). Известны критические значения Стьюдента для различных уровней значимости
При уровне значимости 0,1 значимыми являются параметры …
Решение:
Чтобы оценить значимость параметров регрессии используется t-критерий Стьюдента. Для каждого коэффициента регрессии 
формулируется нулевая гипотеза 
при альтернативной гипотезе 
Затем рассчитывается фактическое значение t-статистики, которое сравнивается с критическим значением Стьюдента 
для требуемого числа степеней свободы и уровня значимости. Если 
, коэффициент 
значим; если 
коэффициент незначим. В нашем случае при уровне значимости 0,1 значимым является параметры 
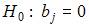
2. Если для среднеквадратической ошибки 
параметра и значения оценки этого параметра 
линейной эконометрической модели выполняется соотношение 
, то это свидетельствует о статистической ______ параметра.
ненадежности среднеквадратической ошибки
надежности среднеквадратической ошибки
Решение:
Превышение среднеквадратической ошибки параметра над значением его оценки свидетельствует о статистической ненадежности параметра.
3. Для уравнения множественной регрессии вида 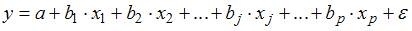на основании 14 наблюдений рассчитаны оценки параметров и записана модель: 
(в скобках указаны значения t-статистики соответствующие параметрам регрессии). Известны критические значения Стьюдента для различных уровней значимости
Для данного уравнения при уровне значимости α=0,05 значимыми являются параметры …
Решение:
Чтобы оценить значимость параметров регрессии используется t-критерий Стьюдента. Для каждого коэффициента регрессии формулируется нулевая гипотеза при альтернативной гипотезе 
. Затем рассчитывается фактическое значение t-статистики, которое сравнивается с критическим значением Стьюдента 
для требуемого числа степеней свободы и уровня значимости. Если , коэффициент значим; если коэффициент незначим. В нашем случае при уровне значимости 0,05 значимыми является параметры 
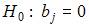
4. Проверка статистически значимого отличия от нуля оценок коэффициентов 
линейной модели
осуществляется путем последовательного сравнения отношений 
( 
–среднеквадратическая ошибка параметра ) с точкой, имеющей распределение …
Решение:
При проверке статистически значимого отличия от нуля оценок коэффициентов линейной регрессионной модели выдвигается гипотеза о нулевом значении оценки параметра. Для каждого коэффициента регрессии 
модели рассчитывают отношение его среднеквадратической ошибки к значению оценки . Полученное значение отношения последовательно сравнивается с точкой, имеющей распределение Стьюдента.
Тема 13: Нелинейные зависимости в экономике
1. Если зависимость объема спроса от цены характеризуется постоянной эластичностью, то моделирование целесообразно проводить на основе …
параболы второй степени
Решение:
Из перечисленных функций только степенная функция характеризуется постоянной эластичностью, следовательно, ее и нужно применить для отражения данной зависимости.
2. Если по результатам анализа поля корреляции замечено, что на интервале изменения фактора меняется характер связи рассматриваемых признаков, прямая связь изменяется на обратную, то моделирование целесообразно проводить на основе …
параболы второй степени
параболы третьей степени
Решение:
Параболу второй степени целесообразно применять в случае, когда на интервале изменения фактора меняется характер связи рассматриваемых признаков, прямая связь изменяется на обратную или обратная на прямую.
3. Нелинейное уравнение регрессии вида 
является _____ моделью ________ регрессии.
Решение:
Нелинейное уравнение регрессии вида является полиномиальной моделью парной регрессии. Теоретическое значение зависимой переменной рассчитывается в данном случае по формуле полинома третьей степени 
, а количество независимых переменных х равно единице.
4. Если с увеличением масштабов производства удельный расход сырья сокращается, то моделирование целесообразно проводить на основе …
параболы второй степени
Решение:
Равносторонняя гипербола обычно используется в эконометрике для характеристики связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции, поскольку она позволяет учесть эффект масштаба, что с увеличением объемов выпускаемой продукции удельные показатели расходов сырья, материалов или топлива обычно падают.
Тема 14: Виды нелинейных уравнений регрессии
1. Степенной моделью не является регрессионная модель …
Решение:
Степенной моделью регрессии является такая модель, в которой независимая переменная х стоит в основании степени, а параметр – в показателе. Такими моделями из приведенных в ответах являются уравнения: 
В уравнении независимая переменная х стоит в показателе степени, а параметр b – в основании, это не степенное уравнение, такая модель является примером показательной зависимости.
2. Среди предложенных нелинейных зависимостей нелинейной по параметрам является …
Решение:
Среди предложенных нелинейных зависимостей зависимость является нелинейной по параметрам, но внутренне линейной, поскольку с помощью логарифмирования ее можно привести к линейному виду. Остальные функции линейны по параметрам, но нелинейны относительно переменных и к линейному виду могут быть приведены с помощью замены переменных.
3. Среди предложенных нелинейных зависимостей нелинейной существенно (внутренне нелинейной) является …
Решение:
Среди предложенных нелинейных зависимостей зависимость является внутренне нелинейной, поскольку с помощью элементарных преобразований или замены переменных ее нельзя привести к линейному виду.
4. Среди предложенных нелинейных зависимостей внутренне линейной является …
Решение:
Среди предложенных нелинейных зависимостей зависимость является внутренне линейной, хотя она и нелинейна по переменным, поскольку с помощью логарифмирования ее можно привести к линейному виду. Остальные функции внутренне нелинейны: они не могут быть приведены к линейному виду.
Тема 15: Линеаризация нелинейных моделей регрессии
1. Для линеаризации нелинейной регрессионной модели используется …
приведение уравнения к виду 1/y
Решение:
Линеаризация – это процедура приведения нелинейной регрессионной модели к линейному виду путем различных математических преобразований. Нелинейная модель является степенной. Приведение ее к линейному виду возможно логарифмированием уравнения. Получаем 
Остальные виды линеаризации не позволяют линеаризовать исходную нелинейную модель.
2. Для преобразования внутренне нелинейной функции может быть применен метод …
разложения функции в ряд Тейлора
Решение:
Функция является внутренне нелинейной, и для нее отсутствует прямое преобразование, которое превратит ее в линейную функцию. Только разложением функции в ряд Тейлора, то есть заменой данной функции суммой полиномов, можно привести данную функцию к линейному виду.
3. Для линеаризации нелинейной функции может быть применен метод …
логарифмирования и замены переменных
разложения функции в ряд Тейлора
потенцирования и замены переменных
обращения и замены переменных
Решение:
Функция 
является внутренне линейной и с помощью логарифмирования может быть преобразована к виду 
, которая является линейной относительно логарифмов переменных. Сделав замену переменных 
, 
, 
, 
, получим линейную функцию 
. Поэтому для линеаризации используется сначала логарифмирование, затем замена переменных.
Тема 16: Оценка качества нелинейных уравнений регрессии
1. При расчете уравнения нелинейной регрессии 
, где y – спрос на продукцию, ед.; x – цена продукции, руб., выяснилось, что доля остаточной дисперсии в общей меньше 20%. Коэффициент детерминации для данной модели попадает в отрезок минимальной длины …
Решение:
Доля остаточной дисперсии в общей меньше 20%, значит, доля объясненной регрессии в общей больше 80%, другими словами, коэффициент детерминации больше 0,8. Поскольку коэффициент детерминации может принимать значения только в интервале [0, 1], то отрезком минимальной длины, в который попадает коэффициент детерминации для данной модели, будет отрезок [0,8; 1].
2. По 20 регионам страны изучалась зависимость уровня безработицы y (%) от индекса потребительских цен x (% к предыдущему году) и построено уравнение в логарифмах исходных показателей: 
. Коэффициент корреляции между логарифмами исходных показателей составил 
. Коэффициент детерминации для модели в исходных показателях равен …
Решение:
Коэффициент детерминации для модели в исходных показателях в данном случае будет равен коэффициенту детерминации для модели в логарифмах исходных показателей, который вычисляется как квадрат коэффициента корреляции, то есть 0,64.
3. Для регрессионной модели 
, где 
– нелинейная функция, 
– рассчитанное по модели значение переменной 
, получены значения дисперсий: 
. Не объяснена моделью часть дисперсии переменной , равная …
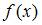
Решение:
Значение индекса детерминации R 2 характеризует долю дисперсии зависимой переменной, объясненную независимой переменной (построенным нелинейным уравнением регрессии). Разность (1-R 2 ) характеризует долю дисперсии зависимой переменной, необъясненную уравнением, эту величину и необходимо определить в задании. Воспользуемся формулой для расчета R 2 : 
. Следовательно, разность 
. Таким образом, часть дисперсии переменной , необъясненная моделью, равна 0,096. Можно также рассчитать это значение через отношение 
4. Для регрессионной модели , где – нелинейная функция, – рассчитанное по модели значение переменной , получено значение индекса корреляции R = 0,64. Моделью объяснена часть дисперсии переменной , равная …
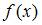
Решение:
Величина, характеризующая долю дисперсии зависимой переменной, объясненную независимой переменной (построенным нелинейным уравнением регрессии), называется индексом (коэффициентом) детерминации – R 2 . Значения индекса детерминации R 2 и индекса корреляции R для нелинейных регрессионных моделей связаны соотношением 
. Следовательно, значение 
.
5. По результатам проведения исследования торговых точек было построено уравнение нелинейной регрессии , где y – спрос на продукцию, ед.; x – цена продукции, руб. Если фактическое значение t-критерия Стьюдента составляет –2,05, а критические значения для данного количества степеней свободы равны 
, 
, 
, то …
при уровне значимости 
можно считать, что эластичность спроса по цене составляет –0,8
при уровне значимости 
можно считать, что эластичность спроса по цене составляет –0,8
эластичность спроса по цене составляет –0,8
при уровне значимости 
можно считать, что эластичность спроса по цене составляет –0,8
Решение:
Для проверки значимости коэффициентов нелинейной регрессии, после линеаризации, как и для уравнения парной линейной регрессии, применяется стандартный алгоритм критерия Стьюдента. Для b формулируется нулевая гипотеза 
при альтернативной гипотезе 
. Затем рассчитывается фактическое значение t-статистики, которое сравнивается с критическим значением Стьюдента для требуемого числа степеней свободы и уровня значимости. Если , коэффициент 
значим; если 
, коэффициент незначим. В нашем случае при уровне значимости коэффициент значим, а при уровнях значимости и незначим.
Тема 17: Временные ряды данных: характеристики и общие понятия
1. В состав любого временного ряда, построенного по реальным данным, обязательно входит _____ компонента.
Решение:
Ряд, построенный по реальным данным, может не содержать тренда, сезонной (циклической) компоненты, однако, он обязательно содержит случайную компоненту.
2. Ряд, уровни которого образуются как сумма среднего уровня ряда и некоторой случайной компоненты, изображен на графике …
Решение:
График ряда, уровни которого образуются как сумма среднего уровня ряда и некоторой случайной компоненты, будет колебаться относительно своего среднего значения.
3. Совокупность значений экономического показателя за несколько последовательных моментов (периодов) времени называется …
Решение:
Совокупность значений экономического показателя за несколько последовательных моментов (периодов) времени называется временным рядом.
4. Выраженную положительную тенденцию содержит ряд …
—
Решение:
Ряд имеет выраженную положительную тенденцию, если уровни ряда увеличиваются с увеличением периода времени t.
Тема 18: Структура временного ряда
1. Значение коэффициента автокорреляции первого порядка характеризует …
тесноту линейной связи
качество модели временного ряда
тесноту нелинейной связи
Решение:
Структура временного ряда определяется по значениям коэффициента автокорреляции, рассчитанным для разных порядков коэффициента автокорреляции. Коэффициент автокорреляции характеризует тесноту связи между уровнями исходного ряда и уровнями этого же ряда, сдвинутыми на значение порядка, а само значение коэффициента корреляции рассчитывается по аналогии с парным коэффициентом линейной корреляции и характеризует тесноту линейной связи между двумя переменными. Поэтому варианты «качество модели временного ряда», «тесноту нелинейной связи» и «значимость тренда» являются неверными.
Видео:Эконометрика. Множественная регрессия и корреляция.Скачать
Тема 2. Классическая и обобщенная модели множественной регрессии
Экономические явления определяются, как правило, большим числом совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимости одной переменной Y от нескольких объясняющих переменных X1, X2, Xn. Эта задача решается с помощью множественного регрессионного анализа.
Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели, включающего отбор факторов и выбор вида уравнения регрессии. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:
— они должны быть количественно измеримыми (качественным факторам необходимо придать количественную определенность);
— между факторами не должно быть высокой корреляционной, а тем более функциональной зависимости, т.е. наличия мультиколлинеарности.
Включение в модель мультиколлинеарных факторов может привести к следующим последствиям:
∙ затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом виде», поскольку факторы связаны между собой; параметры линейной регрессии теряют экономический смысл;
∙ оценки параметров ненадежны, имеют большие стандартные ошибки и меняются с изменением объема наблюдений.
Пусть 
— матрица-столбец значений зависимости переменной размера п,
— матрица значений объясняющих переменных;
— матрица-столбец (вектор) параметров размера т+1;
— матрица-столбец (вектор) остатков размера п;
Тогда в матричной форме модель множественной линейной регрессии запишется следующим образом:
(1)
При оценке параметров уравнения регрессии (вектора b) применяется метод наименьших квадратов (МНК). При этом делаются определенные предпосылки.
1. В модели (1) ε – случайный вектор, Х – неслучайная (детерминированная) матрица.
2. Математическое ожидание величины остатков равно нулю: М(ε) = 0п.
3. Дисперсия остатков εi постоянна для любого i (условие гомоскедастичности), остатки εi и εj при i ≠ j не коррелированны: 
4. ε – нормальное распределенный случайный вектор, т.е. ε
5. r (X) = m+1 
Согласно методу наименьших квадратов неизвестные параметры выбираются таким образом, чтобы сумма квадратов отклонений фактических значений от значений, найденных по уравнению регрессии, была минимальной:
Решением этой задачи является вектор 
Одной из наиболее эффективных оценок адекватности модели является коэффициент детерминации R 2 , определяемый формулой:
Коэффициент детерминации характеризует долю вариации зависимой переменной, обусловленной регрессией или изменчивостью объясняющих переменных. Чем ближе R 2 к единице, тем лучше построенная регрессионная модель описывает зависимость между объясняющими и зависимой переменной.
Следует иметь в виду, что при включении в модель новой объясняющей переменной, коэффициент детерминации увеличивается, хотя это и не обязательно означает улучшение качества регрессионной модели. В этой связи лучше использовать скорректированный (поправленный) коэффициент детерминации 
, рассчитываемый по формуле:
,
п – число наблюдений;
т – число параметров при переменных х.
Из формулы следует, что с включением в модель дополнительных переменных разница между значениями и R 2 увеличивается. Таким образом, скорректированный коэффициент детерминации может уменьшаться при добавлении в модель новой объясняющей переменной, не оказывающей существенного влияния на результативный признак.
Но использование только коэффициента детерминации для выбора наилучшего уравнения регрессии может оказаться недостаточным.
Средняя относительная ошибка аппроксимации рассчитывается по формуле:
Значимость уравнения регрессии в целом сводится к проверке гипотезы об одновременном равенстве нулю всех коэффициентов регрессии при факторных признаках, т.е. гипотезы:
Если данная гипотеза не отклоняется, то делается вывод о том, что совокупное влияние всех факторных признаков 
, включенных в модель, не зависимую переменную у можно считать статистически несущественным. Проверка данной гипотезы осуществляется на основе дисперсионного анализа.
Основной идеей дисперсионного анализа является разложение общей суммы квадратов отклонений результативной переменной 
от среднего значения 
на «объясненную» и «остаточную»:
 | = |  | + |  |
| Общая сумма квадратов отклонений | Сумма квадратов отклонений, объясненная регрессией | Остаточная сумма квадратов отклонений |
Для приведения дисперсий к сопоставимому виду, определяют дисперсии на одну степень свободы. Результаты вычислений заносят в специальную таблицу дисперсионного анализа:
| Компоненты дисперсии | Сумма квадратов | Число степеней свободы | Оценка дисперсии на одну степень свободы |
| Общая | |  | ——- |
| Объясненная | |  |  |
| Остаточная | |  |  |
В данной таблице п – число наблюдений, т – число параметров при переменных х.
Сравнивая полученные оценки объясненной и остаточной дисперсии на одну степень свободы, определяют значение F-критерия Фишера, используемого для оценки значимости уравнения регрессии:
С помощью F-критерия проверяется нулевая гипотеза о равенстве дисперсий Н0: SR 2 = S 2 .
Если нулевая гипотеза справедлива, то объясненная и остаточная дисперсии не отличаются друг от друга. Для того, чтобы уравнение регрессии было значимо в целом (гипотеза Н0 была отвергнута) необходимо, чтобы объясненная дисперсия превышала остаточную в несколько раз. Критическое значение F-критерия определяется по таблице Фишера — Снедекора.
Расчетное значение сравнивается с табличным, и если оно превышает табличное (Fрасч > Fтабл), то гипотеза Н0 отвергается, и уравнение регрессии признается значимым.
Если Fрасч 2 следующим соотношением:
т – число параметров при переменных х;
п – число наблюдений.
Оценка значимости коэффициентов регрессии сводится к проверке гипотезы о равенстве нулю коэффициента регрессии при соответствующем факторном признаке, т.е. гипотезы:
Проверка гипотезы проводится с помощью t-критерия Стьюдента. Для этого расчетное значение t-критерия:
,
— коэффициент регрессии при 
;
— средняя квадратическая ошибка коэффициента регрессии .
сравнивается с табличным tтабл при заданном уровне значимости α и числе степеней свободы
Если расчетное значение превышает табличное, то гипотезу о несущественности коэффициента регрессии можно отклонить.
Рассмотрим интерпретацию параметров модели линейной множественной регрессии. В линейной модели множественной регрессии 
коэффициенты регрессии характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизменном значении других факторов, закрепленных на среднем уровне.
На практике часто бывает необходимо сравнить влияние на зависимую переменную различных объясняющих переменных, когда последние выражаются разными едиными измерениями. В этом случае используют стандартизованные коэффициенты регрессии 
и коэффициенты эластичности 
.
Уравнение регрессии в стандартизованной форме:
где: 
. – стандартизованные переменные.
В результате такого нормирования средние значения всех стандартизованных переменных равны нулю, а дисперсии равны единице, т.е. 
.
Коэффициенты «чистой» регрессии связаны со стандартизованными коэффициентами следующим соотношением: 
Стандартизованные коэффициенты показывают, на сколько стандартных отклонение (сигм) изменится в среднем результат, если соответствующий фактор изменится на одно стандартное отклонение (одну сигму) при неизменном среднем уровне других факторов. Сравнивая стандартизованные коэффициенты друг с другом, можно ранжировать факторы по силе их воздействия на результат.
Средние коэффициенты эластичности вычисляются по формуле:
Коэффициент эластичности показывает, на сколько процентов (от средней) изменится в среднем Y при увеличении только фактора Xi на 1%.
Рассмотрим пример построения модели множественной регрессии с помощью средств приложения Microsoft Excel.
Пример 1. По данным, представленным в таблице 2, изучается зависимость балансовой прибыли предприятия торговли Y (тыс. руб.) от следующих факторов:
Х1 – объем товарных запасов, тыс. руб.;
Х2 – фонд оплаты труда, тыс. руб.;
Х3 – издержки обращения, тыс. руб.;
Х4 – объем продаж по безналичному расчету, тыс. руб.
| Месяц | Y | Х1 | Х2 | Х3 | Х4 |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1. | 41321,57 | 300284,10 | 19321,80 | 42344,92 | 100340,02 |
| 2. | 40404,27 | 494107,21 | 20577,92 | 49000,43 | 90001,35 |
| 3. | 37222,12 | 928388,75 | 24824,91 | 50314,52 | 29301,98 |
| 4. | 37000,80 | 724949,11 | 28324,87 | 48216,41 | 11577,42 |
| 5. | 29424,84 | 730855,33 | 21984,07 | 3301,30 | 34209,84 |
| 6. | 20348,19 | 2799881,13 | 11000,02 | 21284,21 | 29300,00 |
| 7. | 11847,11 | 1824351,20 | 4328,94 | 28407,82 | 19513,92 |
| 8. | 14320,64 | 1624500,80 | 7779,41 | 40116,00 | 17343,20 |
| 9. | 18239,46 | 1115300,93 | 18344,11 | 32204,98 | 4391,00 |
| 10. | 22901,52 | 1200947,52 | 20937,31 | 30105,29 | 14993,25 |
| 11. | 27391,92 | 1117850,93 | 27344,30 | 40294,40 | 104300,00 |
| 12. | 44808,37 | 1379590,02 | 31939,52 | 42239,79 | 119804,33 |
| 13. | 40629,28 | 588365,77 | 29428,60 | 55584,35 | 155515,15 |
| 14. | 31324,80 | 434281,91 | 30375,82 | 49888,17 | 60763,19 |
| 15. | 34847,92 | 1428243,59 | 33000,94 | 59866,55 | 8763,25 |
| 16. | 33241,32 | 1412181,59 | 31322,60 | 49975,79 | 4345,42 |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 17. | 29971,34 | 1448274,10 | 20971,82 | 3669,92 | 48382,15 |
| 18. | 17114,90 | 4074616,71 | 11324,93 | 26032,95 | 10168,00 |
| 19. | 8944,94 | 1874298,99 | 8341,52 | 29327,21 | 22874,40 |
| 20. | 17499,58 | 1525436,47 | 10481,14 | 40510,01 | 29603,05 |
| 21. | 19244,80 | 1212238,89 | 18329,90 | 37444,69 | 16605,16 |
| 22. | 34958,32 | 1154327,22 | 29881,52 | 36427,22 | 32124,63 |
| 23. | 44900,83 | 1173125,03 | 34928,60 | 51485,62 | 200485,00 |
| 24. | 57300,25 | 1435664,93 | 41824,92 | 49959,92 | 88558,62 |
1. Для заданного набора данных постройте линейную модель множественной регрессии.
2. Оцените точность и адекватность построенного уравнения регрессии.
3. Выделите значимые и незначимые факторы в модели.
4. Постройте уравнение регрессии со статистически значимыми факторами. Дайте экономическую интерпретацию параметров модели.
Для получения отчета по построению модели в среде EXCEL необходимо выполнить следующие действия:
1. В меню Сервис вбираем строку Анализ данных. На экране появится окно
2. В появившемся окне выбираем пункт Регрессия. Появляется диалоговое окно, в котором задаем необходимые параметры (рис. 2).
3. Диалоговое окно рис. 2 заполняется следующим образом:
Входной интервал Y – диапазон (столбец), содержащий данные со значениями объясняемой переменной;
Входной интервал X – диапазон (столбцы), содержащий данные со значениями, объясняющих переменных.
Метки – флажок, который указывает, содержат ли первые элементы отмеченных диапазонов названия переменных (столбцов) или нет;
Константа-ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении регрессии (β0);
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона, в котором будет сохранен отчет по построению модели;
Новый рабочий лист – можно задать произвольное имя нового листа, в котором будет сохранен отчет.
Если необходимо получить значения и графики остатков (ei), установите соответствующие флажки в диалоговом окне. Нажмите кнопку ОК.
Вид отчета о результатах регрессионного анализа представлен на рис. 3.
Рассмотрим таблицу «Регрессионная статистика».
Множественный R – это 
R—квадрат – это R 2 . В нашем примере значение R 2 = 0,8178 свидетельствует о том, сто изменения зависимой переменной Y (балансовой прибыли) в основном (на 81,78%) можно объяснить изменениями включенных в модель объясняющих переменных – X1, X2, X3, X4. такое значение свидетельствует об адекватности модели.
Нормированный R—квадрат – поправленный (скорректированный по числу степеней свободы) коэффициент детерминации.
Стандартная ошибка регрессии 
— необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии); п – число наблюдений (в нашем примере равно 24), т – число объясняющих переменных (в нашем примере равно 4).
Наблюдения – число наблюдений п.
Рассмотрим таблицу с результатами дисперсионного анализа.
df – degrees of freedom – число степеней свободы связано с числом единиц совокупности п и с числом определяемых по ней констант (т +1).
SS – sum of squares – сумма квадратов (регрессионная (RSS – regression sum of squares), остаточная (ESS – error sum of squares) и общая (TSS – total sum of squares), соответственно).
MS – mean sum – сумма квадратов на одну степень свободы.
F – расчетное значение F–критерия Фишера. Если нет табличного значения, то для проверки значимости уравнения регрессии в целом можно посмотреть Значимость F. На уровне значимости α = 0.05 уравнение регрессии признается значимым в целом, если Значимость F 2 = 0,8144 свидетельствует о том, что вариация зависимой переменной Y (балансовой прибыли) по-прежнему в основном (на 81,44%) можно объяснить вариацией включенных в модель объясняющих – X2, и X4. это свидетельствует об адекватности модели.
Значение поправленного коэффициента детерминации (0,7967) возросло по сравнению с первой моделью, в которую были включены все объясняющие переменные (0,7794).
Стандартная ошибка регрессии во втором случае меньше, чем в первом (5515 Fα;m-p;m-p, где р – число регрессоров.
Мощность теста (вероятность отвергнуть гипотезу об отсутствии гетероскедастичности, когда гетероскедастичность действительно нет) максимальна, если выбирать т порядка п/3.
Тест Голдфельда-Квандта позволяет выявить факт наличия гетероскедастичности, но не позволяет описать характер зависимостей дисперсий ошибок регрессии количественно.
Если прослеживается влияние результатов предыдущих наблюдений на результаты последующих, случайные величины (ошибки) εi в регрессионной модели не оказываются независимыми. Такие модели называются моделями с наличием автокорреляции.
Как правило, если автокорреляция присутствует, то наибольшее влияние на последующее наблюдение оказывает результат предыдущего наблюдения. Наличие автокорреляции между соседними уровнями ряда можно определить с помощью теста Дарбина-Уотсона. Расчетное значение определяется по следующей формуле:
.
Затем по таблицам находятся пороговые значения dв и dн. если расчетное значение:
— dв ЕSS1). Для нашего примера получаем: F = 3,987Е+08 / 6,04Е+07 = 6,58.
Для того, чтобы узнать табличное значение, воспользуемся встроенной в EXCEL функцией FРАСПОБР(0,05;6;6) с параметрами 0,05 – заданная вероятность ошибки гипотезы Н0; т-р = 8-2 = 6; т-р = 6 – параметры распределения Фишера. Данная функция находится в категории «статистических» функций.
Статистика Fрасч больше табличного значения FРАСПОБР(0,05;6;6) = 4,28. Следовательно, модель гетороскедастична.
Пример 3. Рассмотрим полученную в примере 1 модель зависимости балансовой прибыли предприятия Y (тыс. руб.) от следующих переменных:
Х2 – фонд оплаты труда, тыс. руб.; Х4 – объем продаж по безналичному расчету, тыс. руб.
Задание: проверить полученную модель на наличие автокорреляции остатков с помощью теста Дарбина-Уотсона.
Прежде всего, по эмпирическим данным необходимо методом наименьших квадратов построить уравнение регрессии и определить значения отклонений 
для каждого наблюдения i (i = 1, 2, …, п).
Для этого в диалоговом окне Регрессия в группе Остатки следует установить одноименный флажок Остатки.
Зачем рассчитываем статистику Дарбина-Уотсона по формуле:
.
Результаты расчетов представлены в таблице 6.
 |  |  ^2 |  ^2 |
| 11211,00896 | 1,3Е+08 | ||
| 9809,816986 | 11211,01 | 1963338,9 | 9,6Е+07 |
| 6652,565001 | 9809,817 | 9968240,1 | 4,4Е+07 |
| 4367,949639 | 6652,565 | 5219467,4 | 1,9Е+07 |
| 1141,570741 | 4367,95 | ||
| 2445,881613 | 1141,571 | 1701226,8 | |
| 687,4294812 | 2445,882 | 3092153,9 | |
| 140,6630821 | 687,4295 | 298953,5 | 19786,1 |
| -4784,81741 | 140,6631 | 2,3Е+07 | |
| -3182,828283 | -4784,82 | 2566369,2 | 1Е+07 |
| -10324,78476 | -3182,83 | 1,1Е+0,8 | |
| 1880,960336 | -10324,8 | ||
| -2301,490224 | 1880,96 | ||
| -6360,626521 | -2301,49 | 4Е+07 | |
| -1887,83539 | -6360,63 | ||
| -1671,617647 | -1887,84 | 46750,112 | |
| 1701,17565 | -1671,62 | ||
| 149,2560547 | 1701,176 | 2408454,4 | 22277,4 |
| -6106,936579 | 149,2561 | 3,7Е+07 | |
| 53,14551195 | -6106,94 | 2824,45 | |
| -4554,494657 | 53,14551 | 2,1Е+07 | |
| -426,4897698 | -4554,49 | ||
| -5970,720141 | -426,49 | 3,6Е+07 | |
| 7331,218328 | -5970,72 | 5,4Е+07 | |
| СУММА: | 6,5Е+08 | 6,4Е+08 |
Таким образом, расчетное значение равно d = 6,5Е+08 / 6,4Е+08 = 1,02.
По таблице критических точек распределение Дарбина-Уотсона для заданного уровня значимости α, числа наблюдений п и количества объясняющих переменных т определить два значения: dн – нижняя граница и dв – верхняя граница (таблица 7).
🎥 Видео
Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать
Интерпретация коэффициента при логарифмировании в уравнениях регрессииСкачать
Эконометрика. Нелинейная регрессия. Степенная функция.Скачать
09 02 Основы множественной регрессииСкачать
Парная и множественная линейная регрессияСкачать
Эконометрика. Линейная парная регрессияСкачать
Математика #1 | Корреляция и регрессияСкачать
Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать
Эконометрика. Построение модели множественной регрессии в Excel.Скачать
9. Дисперсионный анализ. Корреляционный анализ. Линейная регрессияСкачать
Математическое Ожидание, Дисперсия, Стандартное Отклонение за 5 минутСкачать
Однофакторная регрессионная модель. Коэффициенты детерминации, корреляции. Критерий ФишераСкачать
Регрессия в ExcelСкачать
Математика| СтепениСкачать
ММХ. Модуль 6. Часть 1. Регрессионный анализСкачать
Метод наименьших квадратов. Линейная аппроксимацияСкачать
РЕГРЕССИОННЫЙ АНАЛИЗ STATISTICA #12Скачать
08 06 Корреляция и регрессияСкачать
