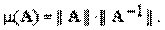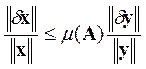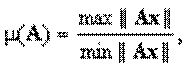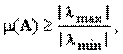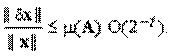Обусловленность задачи решения систем линейных алгебраических уравнений

(или обусловленность задач и вычислений)

Рассмотрим систему линейных алгебраических уравнений

,

Будем считать, что det A ¹ 0, .

Матрица А и вектор правой части во многих случаях задаются приближенно. Они получены либо в процессе эксперимента, либо в процессе каких-то промежуточных расчетов, содержащих соответственно погрешности эксперимента либо погрешности округления.

Естественно встает вопрос, как эти погрешности (возмущения) исходных данных влияют на точность решения. Чтобы на него ответить, надо познакомиться с особой характеристикой матриц, которую называют обусловленностью [3].

Таким образом, обусловленность характеризует устойчивость решения системы относительно исходных данных

Введем еще одно определение: задача решения СЛАУ является корректной, если решение существует, единственно (detA¹0) и непрерывно зависит от исходных данных (матриц А и В), т.е. малым изменениям исходных данных соответствуют малые изменения решения задачи.

Прежде всего, оговорим различие между плохо обусловленной задачей и плохо обусловленными вычислениями.

Если задача плохо обусловлена, то никакие усилия, потраченные на организацию изощренных вычислений, не могут дать правильный ответ, исключая случайность. С плохо обусловленными задачами можно столкнуться при расчетах стержневых систем методами строительной механики, например,

• при расчете рам методом перемещений, если два узла соединены очень жесткой частью конструкции;
• или при расчете конструкции методом сил, если выбрать основную систему так, что перемещение в устраняемой связи, соответствующее приложенной в ней паре нагрузок, равно или меньше перемещений в других устраненных связях от этой же нагрузки.

Все плохо обусловленные вычисления являются результатом применения численно неустойчивых алгоритмов. Например, метод исключения Гаусса без выбора главного элемента может обладать таким недостатком.

У плохо обусловленной матрицы обратная матрица является неустойчивой, т.е. элементы обратной матрицы значительно изменяются при малом изменении элементов исходной матрицы.

n Пример 3.7.Рассмотримплохо обусловленнуюсистему, записанную в матричном виде:

Если изменить правые части на 0,1 и принять их равными

то получим решение .

Если принять величину 1-го коэффициента в 1-ом уравнении равной 4,99 вместо 5, то получим решение .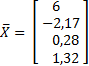

Существенно изменится при этом и обратная матрица.

Следует отметить, что чем больше порядок системы, тем сильнее сказывается влияние небольших возмущений коэффициентов системы на ее решение.

Обусловленность матрицы (системы) является качественной характеристикой, хотя мы будем стараться оценить ее количественно. Существует несколько способов оценки обусловленности.

Например, обусловленность матрицы (системы) можно оценить с помощью величины, называемой мерой обусловленности m(A):

где – норма матрицы А; – норма обратной матрицы.

Число m(A), часто обозначаемое cond A (от английского слова conditioned — «обусловленный»), служит также коэффициентом роста относительных погрешностей при неточном задании элементов матрицы А.

Чем больше m(A) ,тем сильнее сказываются возмущения в исходных данных на решении системы линейных уравнений. Если число m(A) велико, то система считается плохо обусловленной. Говорить о том, «что такое хорошо, а что такое плохо» в отрыве от контекста решаемой задачи почти бессмысленно, так как здесь могут играть роль размерность задачи, точность, с которой должно быть найдено ее решение, точность представления чисел в ЭВМ и т.п. Однако можно дать оценку снизу меры обусловленности. Число обусловленности m(A) не может быть меньше 1. Матрица, а соответственно и система, будет хорошо обусловленной, если m(A) стремится к единице.

n Пример 3.8. Оценим обусловленность матриц А и В:

A =

Решение:

Обратные матрицы равны:

=

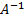
Вычислим меры обусловленности. Для этого найдем нормы матрицы А:

Мера обусловленности m(A) = 12´0,292=4,506 невелика и матрица А хорошо обусловлена.

Нормы матрицы В:

Мера обусловленности m(B) = 21´8421=176841 очень большая и матрица Вплохо обусловлена.

Примеры решения СЛАУ с использованием электронных таблиц MS Excel

Реализация метода Гаусса

Рассмотрим решение системы линейных алгебраических уравнений (пример 3.1) методом Гаусса, используя таблицы Excel.

Последовательность действий

Введем расширенную матрицу системы, как показано на рис.3.3, в ячейки А3:D5.

Рис.3.3. Реализация метода Гаусса в MS Excel

Прямой ход метода Гаусса.

1. Поделим элементы 1-ой строки на а_{11 .}Для этого в ячейку А7 введем формулу

и скопируем ее вправо до конца строки.

2. Умножим элементы 1-ой строки на (–а₂₁ ) и прибавим ко 2-й строке. Для этого введем формулу

и скопируем ее вправо до конца строки.

3. Умножим элементы 1-ой строки на (–а₃₁ ) и прибавим к 3-й строке. Для этого введем формулу

и скопируем ее вправо до конца строки.

Таким образом исключили неизвестное х₁ из 2-го и 3-го уравнений системы (смотри 1-й шаг рис.3.3).

Осталось исключить неизвестное х₂ из 3-го уравнения системы. Для этого реализуем описанный выше алгоритм для 2-й и 3-й строк (смотри 2-й шаг рис.3.3).

На этом прямой ход метода Гаусс закончен, матрица системы приведена к треугольному виду.

Обратный ход метода Гаусса.

Найдем последовательно неизвестные, начиная с последней строки. Для этого в ячейки G12:G14 запишем формулы:

G3=D12-C12*G4 (для вычисления x₂);

G2=D11-C11*G4-B11*G3 (для вычисления x₁).

Видео:Решение систем линейных алгебраических уравнений методом Крамера.Скачать

Обусловленность систем линейных уравнений

Две на первый взгляд похожие системы линейных уравнений могут обладать различной чувствительностью к погрешностям задания входных данных. Это свойство связано с понятием обусловленности системы уравнений.

Числом обусловленности линейного оператора A, действующего в нормированном пространстве а также числом обусловленности системы линейных уравнений Ax = у назовем величину

Таким образом, появляется связь числа обусловленности с выбором нормы.

Предположим, что матрица и правая часть системы заданы неточно. При этом погрешность матрицы составляет dA, а правой части — dу. Можно показать, что для погрешности dx имеет место следующая оценка ( ):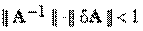

В частности, если dA = 0, то

При этом решение уравнения Ax = у не при всех у одинаково чувствительно к возмущению dу правой части.

Свойства числа обусловленности линейного оператора:

1.

причем максимум и минимум берутся для всех таких x, что Как следствие,

2.

3

где и — соответственно минимальное и максимальное по модулю собственные значения матрицы A. Равенство достигается для самосопряженных матриц в случае использования евклидовой нормы в пространстве

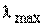
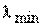
4.

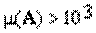
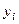
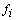
Матрицы с большим числом обусловленности (ориентировочно ) называются плохо обусловленными матрицами. При численном решении систем с плохо обусловленными матрицами возможно сильное накопление погрешностей, что следует из оценки для погрешности dx. Исследуем вопрос о погрешности решения, вызванной ошибками округления в ЭВМ при вычислении правой части. Пусть t — двоичная разрядность чисел в ЭВМ. Каждая компонента вектора правой части округляется с относительной погрешностью Следовательно,

Таким образом, погрешность решения, вызванная погрешностями округления, может быть недопустимо большой в случае плохо обусловленных систем.

Итак – принципиально остаются две проблемы –

1.не обеспечивается обоснованная сходимость алгоритма к единственной (в случае модельного примера- истинной) структуре и

2. Не разрешено противоречие о неадекватности моделей шаговой регрессии на новых точках, не участвовавших при оценке параметров модели. Возможно ли, если не обеспечить такую адекватность при других способах синтеза моделей, то хотя бы найти путь к решению такой задачи (возможно и адекватность определить другим способом )

Для АШР даже в случае применения для МНК оценки процедуры Грамма-Шмидта не разрешается вопрос о единственности модели – просто оценки параметров становятся наиболее точными и несмещенными

Т.о. гарантированное нахождение всего множества подходящих решений в реальных задачах (при 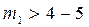— количество линейных входных аргументов и степени ПП p >3) получим только после полного

перебора всех подструктур полной структуры как в методе всех регрессий (у Дрейпера и Смита). Тогда мы найдем всете модели, в которых все аргументы входят с уровнем значимости не менее чем заданный. Со всеми выше описанными проблемами – а какая же из них, из этого множества та, которая действительно наша.

Можно еще добавить камень в огород АШР о неиспользуемой возможности вариации уровнем значимости для учета уровня шума в данных

Именно эту проблему предлагает решать МГУА с помощью введения понятия внешних критериев.

Необходимое примечание.

при 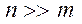все типы АШР МВИ, МГУА, другие целесообразные подходы, дают практически одинаково эффективные (или неэффективные) решения. Кривые критериев одинаково асимптотически стремятся к некоторому ненулевому уровню, при подходе к которому и определяется единственная модель.

Каждый из них это делает по своему, и определить адекватность метода по сходимости к нужной модели можно только построив соответствующий вашей задаче модельный пример.

Однако наиболее распространенный случай – это когда число точек невелико , тогда мы здесь решаем не переопределенную задачу (здесь точного решения нет и мы ищем среди плохих решений наилучшие), а близкую к определенной — вернее даже когда неизвестно, задача переопределена – определена или недоопределена.То есть включается сюда и совсем, казалось бы некорректная задача.

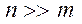
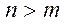
И наиболее эффективный подход к решению структурно-параметрического синтеза при данных условиях демонстрирует МГУА

Как видим нарушение уже первого условия порождаетнеобходимомость разрешения проблемы множественности моделей не прибегая к процедуре полного перебора –надо предложить какой-то принцип, позволяющий найти путь к истинной или квазиистинной модели без полного перебора претендентов моделей.

Следующая проблема не менее реальна и еще более запутывает задачу поиска структуры. – проблема шума в данных –мы помним что при это нарушаются свойства проекционности аппарата МНК – нарушаются свойства оценок, но проблема в том что на зашумленных данных найти истинную структуру вообще может бытььпроблематично – если неизвестны х-ки шума и точки их приложения алгоритм будет тупо подстраиваться под шум.

Основная проблема– проблема необоснованности выбора структуры модели классическими АШГ многократно обостряется в связи с тем что порог используемый критерием Фишера в виде уровня значимости

на самом деле регулирует не только риск ошибки

– его выбор должен учитывать уровень шума и точки его приложения.

Ведь увеличение уровня шума например на выходе неизбено требует загрубить модель (не подстраивать ее под шум) а значит изменить уровень увеличить значимости с тем чтобы более жестко фильтровать апгументы в модель и ее упрощать .

Гораздо сложнее учесть шумы на входе тем более если они проходят нелинейное преобразование модели.

Однако методологически механизмов учета данных коррекций в агоритмах нет что делает выбор структур в условиях шума необоснованным.

Видео:Решение системы уравнений методом ГауссаСкачать

Численные методы решения СЛАУ

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Постановка задачи

Прикладные задачи, характерные для проектирования современных объектов новой техники, часто сводятся к многомерным в общем случае нелинейным уравнениям, которые решаются методом линеаризации, т.е. сведением нелинейных уравнений к линейным. В общем случае система [math]n[/math] уравнений с [math]n[/math] неизвестными записывается в виде

где [math]f_1,f_2,ldots,f_n[/math] — функции [math]n[/math] переменных, нелинейные или линейные ( [math]x_i[/math] в функции [math]f_i[/math] входят в первых или частично в нулевых степенях). Здесь рассматривается частный случай задачи (1.1) — линейная неоднородная задача для систем линейных алгебраических уравнений (СЛАУ), которая сокращенно записывается в виде

где [math]A=(a_in mathbb^[/math] — действительная матрица размера [math](ntimes n),

i,,j[/math] — переменные, соответствующие номерам строк и столбцов (целые числа); [math]b=(b_1,ldots,b_n)^Tin mathbb^n[/math] — вектор-столбец размера [math](ntimes1),

x=(x_1,ldots,x_n)^Tin mathbb^n[/math] — вектор-столбец неизвестных, [math]mathbb^n[/math] — n-мерное евклидово пространство, верхний индекс [math]T[/math] здесь и далее обозначает операцию транспонирования. Требуется найти решение [math]x_= (x_,ldots, x_)^Tin mathbb^n[/math] системы (1.2), подстановка которого в (1.2) приводит к верному равенству [math]Ax_=b[/math] .

1. Из линейной алгебры известно, что решение задачи (1.2) существует и единственно, если детерминант матрицы [math]A[/math] отличен от нуля, т.е. [math]det A equiv |A|ne0[/math] ( [math]A[/math] — невырожденная матрица, называемая также неособенной).

2. Поставленная задача часто именуется первой задачей линейной алгебры. Подчеркнем, что в ней входными (исходными) данными являются матрица [math]A[/math] и вектор [math]b[/math] , а выходными — вектор [math]x[/math] .

3. Задача (1.2) имеет следующие особенности:

а) задача линейная (все переменные [math]x_[/math] , входящие в систему, имеют степени не выше первой) и неоднородная [math](bne0)[/math] ;

б) количество уравнений равно количеству неизвестных (система замкнута);

в) количество уравнений для некоторых практических задач велико: kcdot10^3

г) при больших [math]n[/math] использовать формулу [math]x=A^b[/math] не рекомендуется в силу трудностей нахождения обратной матрицы.

4. Важнейшим признаком любой математической задачи, который надо в первую очередь принимать во внимание при ее анализе и выборе метода решения, является ее линейность или нелинейность. Это связано с тем, что нелинейные задачи с вычислительной точки зрения являются наиболее трудными. Так, нелинейная задача (1.1) является достаточно сложной при числе уравнений [math]n[/math] , пропорциональном [math]10^2[/math] , а линейная задача — при [math]n[/math] , пропорциональном [math]10^6[/math] .

Видео:Матричный метод решения систем уравненийСкачать

Число обусловленности

Характер задачи и точность получаемого решения в большой степени зависят от ее обусловленности, являющейся важнейшим математическим понятием, влияющим на выбор метода ее решения. Поясним это понятие на примере двумерной задачи: [math]begina_x_1+ a_x_2=b_1,\ a_x_1+ a_x_2=b_2.end[/math] . Точным решением этой задачи является вектор [math]x_= (x_, x_)^T[/math] , компоненты которого определяются координатами точки пересечения двух прямых, соответствующих уравнениям [math]a_x_1+ a_x_2=b_1,[/math] [math]a_x_1+ a_x_2=b_2[/math] (рис. 1.1,а).

На рис. 1.1,б применительно к трем наборам входных данных, заданных с некоторыми погрешностями и соответствующих различным системам линейных уравнений, иллюстрируется характер обусловленности системы. Если [math]det A[/math] существенно отличен от нуля, то точка пересечения пунктирных прямых, смещенных относительно сплошных прямых из-за погрешностей задания [math]A[/math] и [math]b[/math] , сдвигается несильно. Это свидетельствует о хорошей обусловленности системы. При [math]det Aapprox0[/math] небольшие погрешности в коэффициентах могут привести к большим погрешностям в решении (плохо обусловленная задача), поскольку прямые близки к параллельным. При [math]det A=0[/math] прямые параллельны или они совпадают, и тогда решение задачи не существует или оно не единственно.

Более строго обусловленность задачи характеризуется числом обусловленности [math]nu(A)= |A|cdot |A^|[/math] , где [math]|A|[/math] — норма матрицы [math]A[/math] , а [math]|A^|[/math] — норма обратной матрицы. Чем больше это число, тем хуже обусловленность системы (при [math]nu(A)approx 10^3div 10^4[/math] система линейных алгебраических уравнений плохо обусловлена). В качестве нормы матрицы может быть принято число, являющееся максимальным из сумм (по модулю) элементов всех строк этой матрицы. Подчеркнем, что реализация хорошей или плохой обусловленности в корректной и некорректной задачах напрямую связана с вытекающей отсюда численной устойчивостью или неустойчивостью. При этом для решения некорректных задач обычно применяются специальные методы или математические преобразования этих задач к корректным.

В численном анализе используются два класса численных методов решения систем линейных алгебраических уравнений:

1. Прямые методы , позволяющие найти решение за определенное число операций. К прямым методам относятся: метод Гаусса и его модификации (в том числе метод прогонки), метод [math]LU[/math] — разложения и др.

2. Итерационные методы , основанные на использовании повторяющегося (циклического) процесса и позволяющие получить решение в результате последовательных приближений. Операции, входящие в повторяющийся процесс, составляют итерацию. К итерационным методам относятся: метод простых итераций, метод Зейделя и др.

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Численные схемы реализации метода Гаусса

Рассмотрим частный случай решения СЛАУ — задачу нахождения решения системы линейных алгебраических уравнений

b=beginb_1\vdots\b_nend[/math] столбцы размеров [math]ntimes 1[/math] . Это означает, что число уравнений совпадает с числом неизвестных, т.е. [math]m=n[/math] . Предполагается, что выполняется условие [math]detequiv|A|ne0[/math] . Тогда по теореме 5.1 решение системы (10.1) существует и единственно.

Согласно изложенному ранее, метод Гаусса содержит две совокупности операций, которые условно названы прямым ходом и обратным ходом.

Прямой ход состоит в исключении элементов, расположенных ниже элементов, соответствующих главной диагонали матрицы [math]A[/math] . При этом матрица [math]A[/math] с помощью элементарных преобразований преобразуется к верхней треугольной, а расширенная матрица [math](Amid b)[/math] — к трапециевидной:

Заметим, что в отличие от общего подхода здесь не требуется приводить расширенную матрицу к упрощенному виду. Считается, что для реализации эффективных численных процедур достаточно свести проблему к решению системы с треугольной матрицей коэффициентов.

Обратный ход состоит в решении системы [math]widetildex= widetilde[/math] .

Видео:Базисные решения систем линейных уравнений (03)Скачать

Алгоритм численного метода Гаусса

а) Положить номер шага [math]k=1[/math] . Переобозначить все элементы расширенной матрицы [math](Amid b)[/math] через [math]a_^,[/math] [math]i=1,ldots,n;[/math] [math]j=1,ldots,n+1[/math] ;

б) Выбрать ведущий элемент одним из двух способов.

Первый способ (схема единственного деления). Выбрать в качестве ведущего элемента [math]a_^ne0[/math] .

Второй способ (схема с выбором ведущего элемента). На k-м шаге сначала переставить [math](n-k+1)[/math] оставшихся уравнений так, чтобы наибольший по модулю коэффициент при переменной [math]x_k[/math] попал на главную диагональ, а затем выбрать в качестве ведущего элемента [math]a_^[/math] .

в) каждый элемент строки, в которой находится ведущий элемент, поделить на него:

г) элементы строк, находящихся ниже строки с ведущим элементом, подсчитать по правилу прямоугольника, схематически показанного на рис. 10.1 (исключить элементы, стоящие ниже ведущего элемента).

Поясним алгоритм исключения на рис. 10.1. Пусть рассчитывается значение [math]a_^[/math] на k-м шаге. Следует соединить элемент [math]a_^[/math] с ведущим элементом [math]a_^[/math] . Получена одна из диагоналей прямоугольника. Вторую диагональ образует соединение элементов [math]a_^[/math] и [math]a_^[/math] . Для нахождения значения [math]a_^[/math] из его текущего значения [math]a_^[/math] вычитается произведение элементов [math]a_^[/math] и [math]a_^[/math] , деленное на ведущий элемент;

д) если [math]kne n[/math] , то перейти к пункту «б», где вместо [math]k[/math] положить [math]k+1[/math] .

Если [math]k=n[/math] , завершить прямой ход. Получена расширенная трапециевидная матрица из элементов [math]a_^[/math] , соответствующая [math]bigl(widetildemid widetildebigr)[/math] .

1. Схема единственного деления имеет ограничение, связанное с тем, что ведущие элементы должны быть отличны от нуля. Одновременно желательно, чтобы они не были малыми по модулю, поскольку тогда погрешности при соответствующем делении будут большими. С этой точки зрения схема с выбором ведущего элемента является более предпочтительной.

2. По окончании прямого хода может быть вычислен определитель матрицы [math]A[/math] путем перемножения ведущих элементов.

3. В расчетных формулах все элементы расширенной матрицы обозначаются одним символом [math]a[/math] , так как они преобразуются по единым правилам.

4. Понятие нормы квадратной невырожденной матрицы позволяет исследовать влияние малых изменений правой части и элементов матрицы на решение систем линейных уравнений. Положительное число [math]A=|A|cdot|A^|[/math] называется числом обусловленности матрицы . Существует и более общее определение числа обусловленности, применимое к вырожденным матрицам: [math]operatornameA= sup_frac: inf_frac[/math] . Чем больше число обусловленности, тем сильнее ошибка в исходных данных сказывается на решении линейной системы. Если число [math]operatornameA[/math] велико, система считается плохо обусловленной, т.е. решение системы может существенно изменяться даже при малых изменениях элементов матрицы [math]A[/math] и столбца свободных членов [math]b[/math] .

Пример 10.3. Найти число обусловленности матрицы системы [math]beginx_1+10x_2=b_1,\ 100x_1+1001x_2=1101. end[/math] Решить систему при [math]b_1=11[/math] и [math]b_1=11,!01[/math] , сравнить близость полученных решений.

По формуле (4.2) для матрицы [math]A=begin 1&10\ 100&1001 end[/math] получаем [math]A^=begin 1001&-10\ -1000&1 end[/math] . Тогда

В результате [math]operatornameA= |A|cdot|A^|=1101cdot1011= 1’113’111[/math] . Очевидно, число обусловленности матрицы системы достаточно велико, поэтому система является плохо обусловленной.

При [math]b_1=11[/math] система имеет единственное решение [math]x_1=1,

x_2=1[/math] , а при [math]b_1=11,!01[/math] , единственное решение [math]x_1=11,!01,

x_2=0[/math] . Несмотря на малое различие в исходных данных: [math]Delta b_1=|11-11,!01|=0,!01[/math] , полученные решения отличаются существенно: [math]Delta x=left| begin1\1 end- begin 11,!01\0 end right|_1=10,!01[/math] , т.е. погрешность [math]Delta x[/math] решения в 1001 раз больше погрешности [math]Delta b_1[/math] правой части системы.

Таким образом, решение плохо обусловленной системы может существенно изменяться даже при малых изменениях исходных данных.

Пример 10.4. Решить систему линейных алгебраических уравнений методом Гаусса (схема единственного деления)

1. Прямой ход. Запишем расширенную матрицу и реализуем прямой ход с помощью описанных преобразований:

Согласно пункту 2 замечаний 10.2 определитель матрицы системы равен произведению ведущих элементов: [math]det=2cdotfraccdot26=26[/math] .

Решая эту систему, начиная с последнего уравнения, находим: [math]x_3=3,

Пример 10.5. Методом Гаусса с выбором ведущего элемента по столбцам решить систему:

1. Прямой ход. Реализуем поиск ведущего элемента по правилу: на k-м шаге переставляются [math](n-k+1)[/math] оставшихся уравнений так, чтобы наибольший по модулю коэффициент при [math]x_k[/math] попал на главную диагональ:

Согласно пункту 2 замечаний 10.2 определитель матрицы системы равен произведению ведущих элементов:

Решая ее, последовательно получаем: [math]x_3=1,

Пример 10.6. Решить систему уравнений методом Гаусса единственного деления

В результате получено решение: [math]x_= begin 1&-1&0&1end^T[/math] .

Видео:Базисные решения систем линейных уравнений (01)Скачать

Метод прогонки для решения СЛАУ

Метод применяется в случае, когда матрица [math]A[/math] — трехдиагональная. Сформулируем общую постановку задачи.

Дана система линейных алгебраических уравнений с трехдиагональной матрицей [math]A[/math] . Развернутая запись этой системы имеет вид

которому соответствует расширенная матрица

Здесь первое и последнее уравнения, содержащие по два слагаемых, знак минус (–) при коэффициенте [math]beta_i[/math] взят для более удобного представления расчетных формул метода.

Если к (10.2) применить алгоритм прямого хода метода Гаусса, то вместо исходной расширенной матрицы получится трапециевидная:

Учитывая, что последний столбец в этой матрице соответствует правой части, и переходя к системе, включающей неизвестные, получаем рекуррентную формулу:

Соотношение (10.3) есть формула для обратного хода, а формулы для коэффициентов [math]P_i,,Q_i[/math] которые называются прогоночными , определяются из (10.2), (10.3). Запишем (10.3) для индекса [math]i-1colon[/math] [math]x_=P_x_i+Q_[/math] и подставим в (10.2). Получим

Приводя эту формулу к виду (10.3) и сравнивая, получаем рекуррентные соотношения для [math]P_i,,Q_icolon[/math]

Определение прогоночных коэффициентов по формулам (10.4) соответствует прямому ходу метода прогонки.

Обратный ход метода прогонки начинается с вычисления [math]x_n[/math] . Для этого используется последнее уравнение, коэффициенты которого определены в прямом ходе, и последнее уравнение исходной системы:

Тогда определяется [math]x_n:[/math]

Остальные значения неизвестных находятся по рекуррентной формуле (10.3).

Видео:Метод Гаусса решения систем линейных уравненийСкачать

Алгоритм решения систем уравнений методом прогонки

Q_1=-frac[/math] (в (10.4) подставить [math]alpha_1=0[/math] ).

2. Вычислить прогоночные коэффициенты: [math]P_2,Q_2;,P_3,Q_3;,ldots;,P_Q_[/math] по формулам (10.4).

2. Значения [math]x_,x_,ldots,x_1[/math] определить по формуле (10.3):

1. Аналогичный подход используется для решения систем линейных алгебраических уравнений с пятидиагональными матрицами.

2. Алгоритм метода прогонки называется корректным, если для всех [math]i=1,ldots,n,

beta_i-alpha_iP_ne0[/math] , и устойчивым, если [math]|P_i| .

3. Достаточным условием корректности и устойчивости прогонки является условие преобладания диагональных элементов в матрице [math]A[/math] , в которой [math]alpha_ine0[/math] и [math]gamma_ine0[/math] [math](i=2,3,ldots,n-1)colon[/math]

и в (10.6) имеет место строгое неравенство хотя бы при одном [math]i[/math] .

4. Алгоритм метода прогонки является экономичным и требует для своей реализации количество операций, пропорциональное [math]n[/math] .

Пример 10.7. Дана система линейных алгебраических уравнений с трехдиагональной матрицей [math]A

gamma_4=0)[/math] . Решить эту систему методом прогонки.

Данная система удовлетворяет условию преобладания диагональных элементов (10.3): в первом уравнении 3″>[math]5>3[/math] , во втором уравнении 3+1″>[math]6>3+1[/math] ; в третьем уравнении 1+2″>[math]4>1+2[/math] , в четвертом уравнении 1″>[math]3>1[/math] . Далее выполняем прямой и обратный ход, учитывая, что расширенная матрица имеет вид

1. Прямой ход. Вычислим прогоночные коэффициенты:

Подчеркнем, что [math]beta_1=-5;

beta_4=3[/math] , так как в (10.2) во втором слагаемом взят знак «минус»:

Подстановкой решения [math]x_=begin 1&1&1&1 end^T[/math] в исходную систему убеждаемся, что задача решена верно. Для данного примера [math]beta_i-alpha_iP_ne0,

i=1,2,3,4;[/math] [math]|P_i| , т.е. метод прогонки оказался корректным и устойчивым (см. пункт 3 замечаний 10.3).

Для наглядности представления информации исходные данные и результаты расчетов поместим в табл. 10.1, где в первых четырех колонках содержатся исходные данные, а в последних трех — полученные результаты.

Пример 10.8. Дана система линейных алгебраических уравнений с трехдиагональной матрицей [math]A[/math] , решить систему методом прогонки:

Результаты расчетов в прямом и обратном ходе занесены в табл. 10.2.

В результате получено решение: [math]x_=begin 1&2&3&4 end^T[/math] . Заметим, что условие преобладания диагональных элементов в данном примере не выполнено, но алгоритм метода прогонки позволил получить точное решение. При этом обратим внимание на небольшой порядок системы и отсутствие погрешностей вычислений.

Пример 10.9. Решить методом прогонки систему уравнений

Расширенная матрица системы имеет вид [math]begin2&1&0&0!!&vline!!&4\ 2&3&-1&-1!!&vline!!&9\ 0&1&-1&3!!&vline!!&12\ 0&0&1&-1!!&vline!!&-4 end[/math] .

1. Прямой ход. Вычислим прогоночные коэффициенты:

Получено решение системы: [math]x_=begin 1&2&-1&3 end^T[/math] . Результаты расчетов приведены в табл. 10.3

Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Метод LU-разложения для решения СЛАУ

Рассмотрим ещё один метод решения задачи (10.1). Метод опирается на возможность представления квадратной матрицы [math]A[/math] системы в виде произведения двух треугольных матриц:

где [math]L[/math] — нижняя, a [math]U[/math] — верхняя треугольные матрицы,

С учётом (10.7) система [math]Ax=b[/math] представляется в форме

Решение системы (10.8) сводится к последовательному решению двух простых систем с треугольными матрицами. В итоге процедура решения состоит из двух этапов.

Прямой ход. Произведение [math]Ux[/math] обозначим через [math]y[/math] . В результате решения системы [math]Ly=b[/math] находится вектор [math]y[/math] .

Обратный ход. В результате решения системы [math]Ux=y[/math] находится решение задачи — столбец [math]x[/math] .

В силу треугольности матриц [math]L[/math] и [math]U[/math] решения обеих систем находятся рекуррентно (как в обратном ходе метода Гаусса).

Из общего вида элемента произведения [math]A=LU[/math] , а также структуры матриц [math]L[/math] и [math]U[/math] следуют формулы для определения элементов этих матриц:

Результат представления матрицы [math]A[/math] в виде произведения двух треугольных матриц (операции факторизации) удобно хранить в одной матрице следующей структуры:

Вычисления на k-м шаге метода LU-разложения удобно производить, пользуясь двумя схемами, изображенными на рис. 10.2.

1. Всякую квадратную матрицу [math]A[/math] , имеющую отличные от нуля угловые миноры

можно представить в виде LU-разложения, причем это разложение будет единственным. Это условие выполняется для матриц с преобладанием диагональных элементов, у которых

2. В результате прямого хода может быть вычислен определитель матрицы [math]A[/math] по свойствам определителя произведения матриц (теорема 2.2) и определителя треугольных матриц:

Видео:Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Алгоритм метода LU-разложение

1. Выполнить операцию факторизации исходной матрицы [math]A[/math] , применяя схемы (рис. 10.2) или формулы (10.9), и получить матрицы [math]L[/math] и [math]U[/math] .

2. Решить систему [math]Lcdot y=b[/math] .

3. Решить систему [math]Ucdot x=b[/math] .

Пример 10.10. Решить систему линейных алгебраических уравнений методом LU-разложения

1. Выполним операцию факторизации:

В результате получены две треугольные матрицы:

Согласно пункту 2 замечаний 10.4, определитель матрицы [math]A[/math] находится в результате перемножения диагональных элементов матрицы [math]Lcolon,det=2cdot0,!5cdot26=26[/math] .

2. Решим систему [math]Lcdot y=b[/math] :

begin2y_1=16,\ 3y_1+0,!5y_2=10,\ y_1+2,!5y_2+26y_3=16. end[/math] . Отсюда [math]beginy_1=8,\ y_2=(10-3cdot8)cdot2=-28,\[4pt] y_3=dfrac=3.end[/math]

3. Решим систему [math]Ucdot x=y:[/math]

beginx_1+0,!5x_2+2x_3=8,\ x_2-10x_3=-28,\ x_3=3.end[/math] . Отсюда [math]begin x_3=3,\ x_2=-28+10cdot3=2,\ x_1=8-2cdot3-0,!5cdot2=1. end[/math]

Пример 10.11. Решить систему линейных алгебраических уравнений методом LU-разложения.

1. Выполним операцию факторизации:

2. Решим систему линейных уравнений [math]Lcdot y=b[/math] :

begin3y_1=5,\ -2y_1+y_2/3=0,\ 2y_1-y_2/3+5y_3=15. end[/math] . Отсюда [math]beginy_1=5/3,\ y_2=10,\ y_3=3.end[/math]

3. Решим систему [math]Ucdot x=y[/math] :

begin x_1-x_2/3=5/3,\ x_2+3x_3=10,\ x_3=3;end Rightarrow

Пример 10.12. Решить систему линейных алгебраических уравнений методом LU-разложения

1. Выполним процедуру факторизации:

В результате получаем матрицы LU-разложения:

2. Решим систему уравнений [math]Lcdot y=b:[/math]

begin2y_1=4,\ 2y_1+2y_2=9,\ y_2-y_3/3=12,\ y_3+5y_4=-4,end!!! Rightarrow

3. Решим систему уравнений [math]Ucdot x=y:[/math]

Отсюда записываем решение исходной системы уравнений: [math]x_= begin1&2&-1&3end^T[/math] .

Видео:Решение системы линейных уравнений методом ГауссаСкачать

Метод квадратных корней для решения СЛАУ

При решении систем линейных алгебраических уравнений с симметрическими матрицами можно сократить объем вычислений почти вдвое.

Пусть [math]A[/math] — симметрическая квадратная матрица системы [math]Ax=b[/math] порядка [math]n[/math] . Решим задачу ее представления в виде

Находя произведение [math]U^Tcdot U[/math] , составим систему уравнении относительно неизвестных элементов матрицы [math]U:[/math]

Система имеет следующий вид:

Из первой строки системы находим

Из второй строки определяем

Из последней строки имеем [math]textstyle<u_=sqrt<a_-sumlimits_^u_^2>>[/math] .

Таким образом, элементы матрицы [math]U[/math] находятся из соотношений

При осуществлении [math]U^TU[/math] -разложения симметрической матрицы могут возникать ситуации, когда [math]u_=0[/math] при некотором [math]i[/math] или подкоренное выражение отрицательно. Для симметрических положительно определенных матриц разложение выполнимо.

Если матрица [math]A[/math] представима в форме [math]U^TU[/math] , то система [math]Ax=b[/math] имеет вид [math]U^TUx=b[/math] . Решение этой системы сводится к последовательному решению двух систем с треугольными матрицами. В итоге процедура решения состоит их двух этапов.

1. Прямой ход. Произведение [math]Ux[/math] обозначается через [math]y[/math] . В результате решения системы [math]U^Ty=b[/math] находится столбец [math]y[/math] .

2. Обратный ход. В результате решения системы [math]Ux=y[/math] находится решение задачи — столбец [math]x[/math] .

Видео:12. Решение систем линейных уравнений методом ГауссаСкачать

Алгоритм метода квадратных корней

1. Представить матрицу [math]A[/math] в форме [math]A=U^Tcdot U[/math] , используя (10.10).

2. Составить систему уравнений [math]U^Tcdot y=b[/math] и найти [math]y[/math] .

3. Составить систему уравнений [math]Ucdot x=y[/math] и найти [math]x[/math] .

Найти решение системы уравнений методом квадратных корней

Решение. 1. Представим матрицу [math]A[/math] в форме [math]A=U^Tcdot U[/math] , используя (10.10):

при [math]i=1[/math] получаем [math]u_= sqrt<a_>= sqrt,,

при [math]i=2[/math] имеем

Таким образом, получили

2. Решим систему [math]U^Tcdot y=b[/math] :

3. Решим систему [math]Ucdot x=y[/math] :

В результате получили решение исходной системы [math]x_1=1,

Видео:Решение системы уравнений методом Крамера 2x2Скачать

Метод простых итераций для решения СЛАУ

Альтернативой прямым методам решения СЛАУ являются итерационные методы, основанные на многократном уточнении [math]x^[/math] , заданного приближенного решения системы [math]Acdot x=b[/math] . Верхним индексом в скобках здесь и далее по тексту обозначается номер итерации (совокупности повторяющихся действий).

Реализация простейшего итерационного метода — метода простых итераций — состоит в выполнении следующих процедур.

1. Исходная задача [math]Acdot x=b[/math] преобразуется к равносильному виду:

где [math]alpha[/math] — квадратная матрица порядка [math]n[/math] ; [math]beta[/math] — столбец. Это преобразование может быть выполнено различными путями, но для обеспечения сходимости итераций (см. процедуру 2) нужно добиться выполнения условия [math]|alpha| .

2. Столбец [math]beta[/math] принимается в качестве начального приближения [math]x^= beta[/math] и далее многократно выполняются действия по уточнению решения, согласно рекуррентному соотношению

или в развернутом виде

3. Итерации прерываются при выполнении условия (где 0″>[math]varepsilon>0[/math] — заданная точность, которую необходимо достигнуть при решении задачи)

1. Процесс (10.12) называется параллельным итерированием , так как для вычисления (k+1)-го приближения всех неизвестных учитываются вычисленные ранее их k-е приближения.

2. Начальное приближение [math]x^[/math] может выбираться произвольно или из некоторых соображений. При этом может использоваться априорная информация о решении или просто «грубая» прикидка. При выполнении итераций (любых) возникают следующие вопросы:

а) сходится ли процесс (10.12), т.е. имеет ли место [math]x^to x_[/math] , при [math]ktoinfty[/math] , где [math]x_[/math] — точное решение?

б) если сходимость есть, то какова ее скорость?

в) какова погрешность найденного решения [math]x^[/math] , т.е. чему равна норма разности [math]bigl|x^-x_bigr|[/math] ?

Ответ на вопросы о сходимости дают следующие две теоремы.

Теорема (10.1) о достаточном условии сходимости метода простых итераций. Метод простых итераций, реализующийся в процессе последовательных приближений (10.12), сходится к единственному решению исходной системы [math]Ax=b[/math] при любом начальном приближении [math]x^[/math] со скоростью не медленнее геометрической прогрессии, если какая-либо норма матрицы [math]alpha[/math] меньше единицы, т.е. [math]|alpha|_s .

1. Условие теоремы 10.1, как достаточное, предъявляет завышенные требования к матрице [math]alpha[/math] , и потому иногда сходимость будет, если даже [math]|alpha|geqslant1[/math] .

2. Сходящийся процесс обладает свойством «самоисправляемости», т.е. отдельная ошибка в вычислениях не отразится на окончательном результате, так как ошибочное приближение можно рассматривать, как новое начальное.

3. Условия сходимости выполняются, если в матрице [math]A[/math] диагональные элементы преобладают, т.е.

и хотя бы для одного [math]i[/math] неравенство строгое. Другими словами, модули диагональных коэффициентов в каждом уравнении системы больше суммы модулей недиагональных коэффициентов (свободные члены не рассматриваются).

4. Чем меньше величина нормы [math]|alpha|[/math] , тем быстрее сходимость метода.

Теорема (10.2) о необходимом и достаточном условии сходимости метода простых итераций. Для сходимости метода простых итераций (10.12) при любых [math]x^[/math] и [math]beta[/math] необходимо и достаточно, чтобы собственные значения матрицы [math]alpha[/math] были по модулю меньше единицы, т.е. [math]bigl|lambda_i(alpha)bigr| .

Замечание 10.7. Хотя теорема 10.2 дает более общие условия сходимости метода простых итераций, чем теорема 10.1, однако ею воспользоваться сложнее, так как нужно предварительно вычислить границы собственных значений матрицы [math]alpha[/math] или сами собственные значения.

Преобразование системы [math]Ax=b[/math] к виду [math]x=alpha x+beta[/math] с матрицей [math]alpha[/math] , удовлетворяющей условиям сходимости, может быть выполнено несколькими способами. Приведем способы, используемые наиболее часто.

1. Уравнения, входящие в систему [math]Ax=b[/math] , переставляются так, чтобы выполнялось условие (10.14) преобладания диагональных элементов (для той же цели можно использовать другие элементарные преобразования). Затем первое уравнение разрешается относительно [math]x_1[/math] , второе — относительно [math]x_2[/math] и т.д. При этом получается матрица [math]alpha[/math] с нулевыми диагональными элементами.

Например, система [math]begin-2,!8x_1+x_2+4x_3=60,\ 10x_1-x_2+8x_3=10,\ -x_1+2x_2-0,!6x_3=20end[/math] с помощью перестановки уравнений приводится к виду [math]begin10x_1-x_2+8x_3=10,\ -x_1+2x_2-0,!6x_3=20,\-2,!8x_1+x_2+4x_3=60, end[/math] где

|4|>|-2,!8|+|1|[/math] , т.е. диагональные элементы преобладают.

Выражая [math]x_1[/math] из первого уравнения, [math]x_2[/math] — из второго, а [math]x_3[/math] — из третьего, получаем систему вида [math]x=alpha x+beta:[/math]

Заметим, что [math]|alpha|_1=max=0,!95 , т.е. условие теоремы 10.1 выполнено.

Проиллюстрируем применение других элементарных преобразований. Так, система [math]begin4x_1+x_2+9x_3=-7,\ 3x_1+8x_2-7x_3=-6,\ x_1+x_2-8x_3=7end[/math] путем сложения первого и третьего уравнений и вычитания из второго уравнения третьего уравнения преобразуется к виду с преобладанием диагональных элементов: [math]begin 5x_1+2x_1+x_3=0,\ 2x_1+7x_2+x_3=-13,\ x_1+x_2-8x_3=7. end[/math]

2. Уравнения преобразуются так, чтобы выполнялось условие преобладания диагональных элементов, но при этом коэффициенты [math]alpha_[/math] не обязательно равнялись нулю.

Например, систему [math]begin1,!02x_1-0,!15x_2=2,!7,\ 0,!8x_1+1,!05x_2=4 end[/math] можно записать в форме [math]beginx_1=-0,!02x_1+0,!15x_2+2,!7,\ x_2=-0,!8x_1-0,!05x_2+4,end[/math] для которой [math]|alpha|_1= max= 0,!85 .

i,j=1,ldots,n[/math] достаточно малы, условие сходимости выполняется.

Видео:Решение системы уравнений методом Крамера.Скачать

Алгоритм метода простых итераций

1. Преобразовать систему [math]Ax=b[/math] к виду [math]x=alpha x+beta[/math] одним из описанных способов.

2. Задать начальное приближение решения [math]x^[/math] произвольно или положить [math]x^=beta[/math] , а также малое положительное число [math]varepsilon[/math] (точность). Положить [math]k=0[/math] .

3. Вычислить следующее приближение [math]x^[/math] по формуле [math]x^= alpha x^+beta[/math] .

4. Если выполнено условие [math]bigl|x^-x^bigr| , процесс завершить и в качестве приближенного решения задачи принять [math]x_cong x^[/math] . Иначе положить [math]k=k+1[/math] и перейти к пункту 3 алгоритма.

Методом простых итераций с точностью [math]varepsilon=0,!01[/math] решить систему линейных алгебраических уравнений:

Решение. 1. Так как [math]|2| , то условие (5.41) не выполняется. Переставим уравнения так, чтобы выполнялось условие преобладания диагональных элементов:

|10|>|2|+|2|[/math] . Выразим из первого уравнения [math]x_1[/math] , из второго [math]x_2[/math] , из третьего [math]x_3:[/math]

Заметим, что [math]|alpha|_1= ma=0,!4 , следовательно, условие сходимости (теорема 10.1) выполнено.

2. Зададим [math]x^=beta= begin 1,!2\1,!3\1,!4 end[/math] . В поставленной задаче [math]varepsilon= 0,!01[/math] .

3. Выполним расчеты по формуле (10.12):

до выполнения условия окончания и результаты занесем в табл. 10.4.

4. Расчет закончен, поскольку выполнено условие окончания [math]bigl|x^-x^ bigr|=0,!0027 .

Приближенное решение задачи: [math]x_cong begin0,!9996& 0,!9995& 0,!9993 end^T[/math] . Очевидно, точное решение: [math]x_=begin 1&1&1 end^T[/math] .

Приведем результаты расчетов для другого начального приближения [math]x^=begin 1,!2&0&0 end^T[/math] и [math]varepsilon=0,!001[/math] (табл. 10.5).

Приближенное решение задачи: [math]x_cong begin 1,!0001& 1,!0001& 1,!0001 end^T[/math] .

Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Метод Зейделя для решения СЛАУ

Этот метод является модификацией метода простых итераций и в некоторых случаях приводит к более быстрой сходимости.

Итерации по методу Зейделя отличаются от простых итераций (10.12) тем, что при нахождении i-й компоненты (k+1)-го приближения сразу используются уже найденные компоненты (к +1) -го приближения с меньшими номерами [math]1,2,ldots,i-1[/math] . При рассмотрении развернутой формы системы итерационный процесс записывается в виде

В каждое последующее уравнение подставляются значения неизвестных, полученных из предыдущих уравнений.

Теорема (10.3) о достаточном условии сходимости метода Зейделя. Если для системы [math]x=alpha x+beta[/math] какая-либо норма матрицы [math]alpha[/math] меньше единицы, т.е. [math]|alpha|_s , то процесс последовательных приближений (10.15) сходится к единственному решению исходной системы [math]Ax=b[/math] при любом начальном приближении [math]x^[/math] .

Записывая (10.15) в матричной форме, получаем

где [math]L,,U[/math] являются разложениями матрицы [math]alpha:[/math]

Преобразуя (10.16) к виду [math]x=alpha x+beta[/math] , получаем матричную форму итерационного процесса метода Зейделя:

Тогда достаточное, а также необходимое и достаточное условия сходимости будут соответственно такими (см. теоремы 10.1 и 10.2):

1. Для обеспечения сходимости метода Зейделя требуется преобразовать систему [math]Ax=b[/math] к виду [math]x=alpha x+beta[/math] с преобладанием диагональных элементов в матрице а (см. метод простых итераций).

2. Процесс (10.15) называется последовательным итерированием , так как на каждой итерации полученные из предыдущих уравнений значения подставляются в последующие. Как правило, метод Зейделя обеспечивает лучшую сходимость, чем метод простых итераций (за счет накопления информации, полученной при решении предыдущих уравнений). Метод Зейделя может сходиться, если расходится метод простых итераций, и наоборот.

3. При расчетах на ЭВМ удобнее пользоваться формулой (10.16).

4. Преимуществом метода Зейделя, как и метода простых итераций, является его «самоисправляемость».

5. Метод Зейделя имеет преимущества перед методом простых итераций, так как он всегда сходится для нормальных систем линейных алгебраических уравнений, т.е. таких систем, в которых матрица [math]A[/math] является симметрической и положительно определенной. Систему линейных алгебраических уравнений с невырожденной матрицей [math]A[/math] всегда можно преобразовать к нормальной, если ее умножить слева на матрицу [math]A^T[/math] (матрица [math]A^TA[/math] — симметрическая). Система [math]A^TAx= A^Tb[/math] является нормальной.

Видео:Решение системы уравнений методом обратной матрицы.Скачать

Алгоритм метода Зейделя

1. Преобразовать систему [math]Ax=b[/math] к виду [math]x=alpha x+beta[/math] одним из описанных способов.

2. Задать начальное приближение решения [math]x^[/math] произвольно или положить [math]x^=beta[/math] , а также малое положительное число [math]varepsilon[/math] (точность). Положить [math]k=0[/math] .

3. Произвести расчеты по формуле (10.15) или (10.16) и найти [math]x^[/math] .

4. Если выполнено условие окончания [math]bigl|x^-x^bigr| , процесс завершить и в качестве приближенного решения задачи принять [math]x_cong x^[/math] . Иначе положить [math]k=k+1[/math] и перейти к пункту 3.

Пример 10.15. Методом Зейделя с точностью [math]varepsilon=0,!001[/math] решить систему линейных алгебраических уравнений:

1. Приведем систему [math]Ax=b[/math] к виду [math]x=alpha x+beta[/math] (см. пример 10.14):

Так как [math]|alpha|_1=max=0,!4 , условие сходимости выполняется.

2. Зададим [math]x^= begin 1,!2&0&0 end^T[/math] . В поставленной задаче [math]varepsilon=0,!001[/math] .

Выполним расчеты по формуле (10.15): [math]begin x_1^=-0,!1cdot x_2^-0,!1cdot x_3^+1,!2,,\[4pt] x_2^=-0,!2cdot x_1^-0,!1cdot x_3^+1,!3,,\[4pt] x_3^=-0,!2cdot x_1^-0,!2cdot x_2^+1,!4,,end!!!!! (k=0,1,ldots)[/math] и результаты занесем в табл. 10.6.

Очевидно, найденное решение [math]x_= begin 1&1&1 end^T[/math] является точным.

4. Расчет завершен, поскольку выполнено условие окончания [math]bigl|x^-x^bigr|= 0,!0004 .

Пример 10.16. Методом Зейделя с точностью [math]varepsilon=0,!005[/math] решить систему линейных алгебраических уравнений:

|5|>|-1|+|-2|[/math] , в данной системе диагональные элементы преобладают. Выразим из первого уравнения [math]x_1[/math] , из второго [math]x_2[/math] , из третьего [math]x_3:[/math]

2. Зададим [math]x^= begin 0&0&0 end^T[/math] . В поставленной задаче [math]varepsilon= 0,!005[/math] .

k=0,1,ldots[/math] и результаты занесем в табл. 10.7.

Очевидно, найденное решение [math]x_= begin 1&1&1 end^T[/math] является точным.

4. Расчет завершен, поскольку выполнено условие окончания [math]bigl|x^-x^bigr|= 0,!001 .

📹 Видео

Метод Жордана-Гаусса решения систем линейных уравнений.Скачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Математика без Ху!ни. Комплексные числа, часть 1. Введение.Скачать