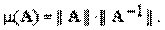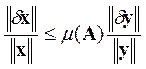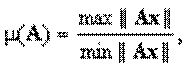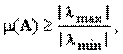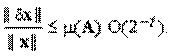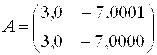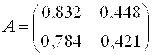Две на первый взгляд похожие системы линейных уравнений могут обладать различной чувствительностью к погрешностям задания входных данных. Это свойство связано с понятием обусловленности системы уравнений.
Числом обусловленности линейного оператора A, действующего в нормированном пространстве 
Таким образом, появляется связь числа обусловленности с выбором нормы.
Предположим, что матрица и правая часть системы заданы неточно. При этом погрешность матрицы составляет dA, а правой части — dу. Можно показать, что для погрешности dx имеет место следующая оценка ( 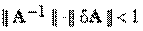

В частности, если dA = 0, то
При этом решение уравнения Ax = у не при всех у одинаково чувствительно к возмущению dу правой части.
Свойства числа обусловленности линейного оператора:
1.
причем максимум и минимум берутся для всех таких x, что 
2.
3
где 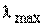
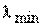
4.
Матрицы с большим числом обусловленности (ориентировочно 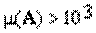
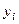
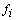
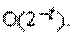
Таким образом, погрешность решения, вызванная погрешностями округления, может быть недопустимо большой в случае плохо обусловленных систем.
Итак – принципиально остаются две проблемы –
1.не обеспечивается обоснованная сходимость алгоритма к единственной (в случае модельного примера- истинной) структуре и
2. Не разрешено противоречие о неадекватности моделей шаговой регрессии на новых точках, не участвовавших при оценке параметров модели. Возможно ли, если не обеспечить такую адекватность при других способах синтеза моделей, то хотя бы найти путь к решению такой задачи (возможно и адекватность определить другим способом )
Для АШР даже в случае применения для МНК оценки процедуры Грамма-Шмидта не разрешается вопрос о единственности модели – просто оценки параметров становятся наиболее точными и несмещенными
Т.о. гарантированное нахождение всего множества подходящих решений в реальных задачах (при 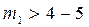
перебора всех подструктур полной структуры как в методе всех регрессий (у Дрейпера и Смита). Тогда мы найдем всете модели, в которых все аргументы входят с уровнем значимости не менее чем заданный. Со всеми выше описанными проблемами – а какая же из них, из этого множества та, которая действительно наша.
Можно еще добавить камень в огород АШР о неиспользуемой возможности вариации уровнем значимости для учета уровня шума в данных
Именно эту проблему предлагает решать МГУА с помощью введения понятия внешних критериев.
Необходимое примечание.
при 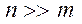
Каждый из них это делает по своему, и определить адекватность метода по сходимости к нужной модели можно только построив соответствующий вашей задаче модельный пример.
Однако наиболее распространенный случай – это когда число точек невелико 
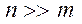
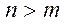


И наиболее эффективный подход к решению структурно-параметрического синтеза при данных условиях демонстрирует МГУА
Как видим нарушение уже первого условия порождаетнеобходимомость разрешения проблемы множественности моделей не прибегая к процедуре полного перебора –надо предложить какой-то принцип, позволяющий найти путь к истинной или квазиистинной модели без полного перебора претендентов моделей.
Следующая проблема не менее реальна и еще более запутывает задачу поиска структуры. – проблема шума в данных –мы помним что при это нарушаются свойства проекционности аппарата МНК – нарушаются свойства оценок, но проблема в том что на зашумленных данных найти истинную структуру вообще может бытььпроблематично – если неизвестны х-ки шума и точки их приложения алгоритм будет тупо подстраиваться под шум.
Основная проблема– проблема необоснованности выбора структуры модели классическими АШГ многократно обостряется в связи с тем что порог используемый критерием Фишера в виде уровня значимости
на самом деле регулирует не только риск ошибки
– его выбор должен учитывать уровень шума и точки его приложения.
Ведь увеличение уровня шума например на выходе неизбено требует загрубить модель (не подстраивать ее под шум) а значит изменить уровень увеличить значимости с тем чтобы более жестко фильтровать апгументы в модель и ее упрощать .
Гораздо сложнее учесть шумы на входе тем более если они проходят нелинейное преобразование модели.
Однако методологически механизмов учета данных коррекций в агоритмах нет что делает выбор структур в условиях шума необоснованным.
Видео:Решение системы уравнений методом ГауссаСкачать

Устойчивость решения СЛАУ относительно исходных данных
(или обусловленность задач и вычислений)
Рассмотрим систему линейных алгебраических уравнений

Будем считать, что det A ¹ 0, 
Матрица А и вектор правой части 
Естественно встает вопрос, как эти погрешности (возмущения) исходных данных влияют на точность решения. Чтобы на него ответить, надо познакомиться с особой характеристикой матриц, которую называют обусловленностью [3].
| G Говорят, что задача, модель или вычисление плохо обусловлены, если они чувствительны к малым изменениям (возмущениям) входящих в нее величин, т.е. исходных данных. В противном случае – хорошо обусловлена. |
Таким образом, обусловленность характеризует устойчивость решения системы относительно исходных данных
Введем еще одно определение: задача решения СЛАУ является корректной, если решение существует, единственно (detA¹0) и непрерывно зависит от исходных данных (матриц А и В), т.е. малым изменениям исходных данных соответствуют малые изменения решения задачи.
Прежде всего, оговорим различие между плохо обусловленной задачей и плохо обусловленными вычислениями.
Если задача плохо обусловлена, то никакие усилия, потраченные на организацию изощренных вычислений, не могут дать правильный ответ, исключая случайность. С плохо обусловленными задачами можно столкнуться при расчетах стержневых систем методами строительной механики, например,
- при расчете рам методом перемещений, если два узла соединены очень жесткой частью конструкции;
- или при расчете конструкции методом сил, если выбрать основную систему так, что перемещение в устраняемой связи, соответствующее приложенной в ней паре нагрузок, равно или меньше перемещений в других устраненных связях от этой же нагрузки.
Все плохо обусловленные вычисления являются результатом применения численно неустойчивых алгоритмов. Например, метод исключения Гаусса без выбора главного элемента может обладать таким недостатком.
У плохо обусловленной матрицы обратная матрица является неустойчивой, т.е. элементы обратной матрицы значительно изменяются при малом изменении элементов исходной матрицы.
n Пример 3.7.Рассмотримплохо обусловленнуюсистему, записанную в матричном виде:
Если изменить правые части на 0,1 и принять их равными


Если принять величину 1-го коэффициента в 1-ом уравнении равной 4,99 вместо 5, то получим решение 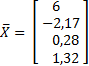
Существенно изменится при этом и обратная матрица.
Следует отметить, что чем больше порядок системы, тем сильнее сказывается влияние небольших возмущений коэффициентов системы на ее решение.
Обусловленность матрицы (системы) является качественной характеристикой, хотя мы будем стараться оценить ее количественно. Существует несколько способов оценки обусловленности.
Например, обусловленность матрицы (системы) можно оценить с помощью величины, называемой мерой обусловленности m(A):
где 

Число m(A), часто обозначаемое cond A (от английского слова conditioned — «обусловленный»), служит также коэффициентом роста относительных погрешностей при неточном задании элементов матрицы А.
Чем больше m(A) ,тем сильнее сказываются возмущения в исходных данных на решении системы линейных уравнений. Если число m(A) велико, то система считается плохо обусловленной. Говорить о том, «что такое хорошо, а что такое плохо» в отрыве от контекста решаемой задачи почти бессмысленно, так как здесь могут играть роль размерность задачи, точность, с которой должно быть найдено ее решение, точность представления чисел в ЭВМ и т.п. Однако можно дать оценку снизу меры обусловленности. Число обусловленности m(A) не может быть меньше 1. Матрица, а соответственно и система, будет хорошо обусловленной, если m(A) стремится к единице.
n Пример 3.8. Оценим обусловленность матриц А и В:
A =
Решение:
Обратные матрицы равны:
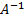
Вычислим меры обусловленности. Для этого найдем нормы матрицы А:
Мера обусловленности m(A) = 12´0,292=4,506 невелика и матрица А хорошо обусловлена.
Нормы матрицы В:
Мера обусловленности m(B) = 21´8421=176841 очень большая и матрица Вплохо обусловлена.
Примеры решения СЛАУ с использованием электронных таблиц MS Excel
Реализация метода Гаусса
Рассмотрим решение системы линейных алгебраических уравнений (пример 3.1) методом Гаусса, используя таблицы Excel.
Последовательность действий
Введем расширенную матрицу системы, как показано на рис.3.3, в ячейки А3:D5.

Прямой ход метода Гаусса.
1. Поделим элементы 1-ой строки на а11 .Для этого в ячейку А7 введем формулу
и скопируем ее вправо до конца строки.
2. Умножим элементы 1-ой строки на (–а21 ) и прибавим ко 2-й строке. Для этого введем формулу
и скопируем ее вправо до конца строки.
3. Умножим элементы 1-ой строки на (–а31 ) и прибавим к 3-й строке. Для этого введем формулу
и скопируем ее вправо до конца строки.
Таким образом исключили неизвестное х1 из 2-го и 3-го уравнений системы (смотри 1-й шаг рис.3.3).
Осталось исключить неизвестное х2 из 3-го уравнения системы. Для этого реализуем описанный выше алгоритм для 2-й и 3-й строк (смотри 2-й шаг рис.3.3).
На этом прямой ход метода Гаусс закончен, матрица системы приведена к треугольному виду.
Обратный ход метода Гаусса.
Найдем последовательно неизвестные, начиная с последней строки. Для этого в ячейки G12:G14 запишем формулы:
G3=D12-C12*G4 (для вычисления x2);
G2=D11-C11*G4-B11*G3 (для вычисления x1).
Видео:Решение систем линейных алгебраических уравнений методом Крамера.Скачать

6.1. Решение систем линейных алгебраических уравнений. Обусловленность матрицы
При исследовании численных методов для решения математических задач необходимо различать свойства самой задачи и свойства вычислительного алгоритма. Для каждой математической задачи принято рассматривать вопрос о ее корректности.
Определение. Говорят, что задача поставлена корректно, если ее решение существует, единственно и непрерывно зависит от входных данных.
Где А — квадратная, неособенная матрица размерности N, и, следовательно, det(A) ≠ 0, тогда существует единственное решение системы. Чтобы убедиться в корректности задачи (6.1) необходимо еще установить непрерывную зависимость решения от входных данных. Входными данными являются правая часть F и элементы матрицы А.
Соответственно, различают устойчивость по правой части, когда возмущается только правая часть F , а матрица А остается неизменной, и коэффициентную устойчивость, когда возмущается только матрица А .
Будем считать, что решение и правая часть задачи (6.1) принадлежат линейному пространству H, состоящему из N-мерных векторов. Введем в H норму, для которой выполнено:
||X||>0, для всех Х≠0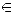
||α X||=| α| ||X||, для любого числа А и Х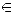
||X+Y||≤||X||+||Y||, для любых X и Y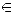
Определение. Нормой матрицы А, подчиненной данной норме векторов, называется число 
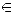
Наряду с системой (6.1) рассмотрим «возмущенную» систему A Xε = Fδ , которая отличается от (6.1) правой частью. Насколько сильно может измениться решение Х В результате изменения правой части?
Определение. Говорят, что система (6.1) устойчива по правой части, если при любых F и Fδ Справедлива оценка || δx||≤ M || δf ||, где M — постоянная, M >0.
Эта оценка выражает факт непрерывной зависимости решения от правой части, то есть показывает, что || δx|| Стремится к нулю при || δf ||Стремящемся к нулю. Наличие устойчивости очень важно при численном решении систем уравнений, так как никогда нельзя задать правую часть F точно. Погрешность δf возникает в результате округления.
Получим оценку для относительной погрешности решения 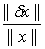
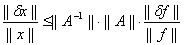
Определение. Число ρ(A)= 
ρ(A)=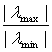
Где λMax , λmin – максимальное и минимальное по модулю собственные значения матрицы A.
Матрицы с большим числом обусловленности называются плохо обусловленными. При численном решении систем с такими матрицами возможно сильное накопление погрешности. При небольших изменениях правой части погрешность решения может оказаться значительной.
Например, для матрицы
Число обусловленности ρ(A)=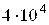
Если взять матрицу
И за правую часть системы вектор F= (1,0000, 0)T, то получим решение 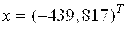
📹 Видео
Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

Решение системы уравнений методом Крамера.Скачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Матричный метод решения систем уравненийСкачать

Решение системы уравнений методом обратной матрицы.Скачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Линейная алгебра, 7 урок, СЛАУ. Матричный методСкачать

Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

Решение системы уравнений методом Гаусса 4x4Скачать

Решение систем линейных уравнений с помощью матрицСкачать

Линейная алгебра, Матрицы: Метод Гаусса. Высшая математикаСкачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Метод Крамера для решения систем линейных алгебраических уравнений (СЛАУ) в ExcelСкачать