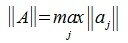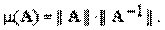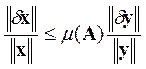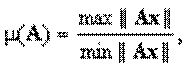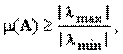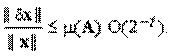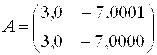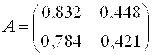Число обусловленности матрицы показывает насколько матрица близка к матрице неполного ранга (для квадратных матриц — к вырожденности).
Рассмотрим систему линейных уравнений
Если матрица A вырожденная, то для некоторых b решение x не существует, а для других b оно будет неединственным. Следовательно, если A почти вырожденная, то можно ожидать, что малые изменения в A и b вызовут очень большие изменения в x. Если же взять в качестве A единичную матрицу, то решение системы (1) будет x=b. Следовательно, если A близка к единичной матрице, то малые изменения в A и b должны влеч за собой малые изменения в x.
Рассмотрим это на численном примере
Как видно из Рис. 1, векторы строки матрицы A — 










Для оченки обусловленности матрицы вычисляют число обусловленности матрицы (обозначается символом «cond»). Для вычисления числа обусловленности введем понятия нормы для векторов x. В качестве нормы возмем l-норму вектора:
Умножая вектор х на матрицу A приводит к новому вектору Ax, норма которого может слишком отличаться от нормы вектора x. Эта чувствительность матрицы A мы хотим измерять. Максимальное и минимальное изменение Ax при изменении можно задать следующими числами:
Отношение Q/q называется числом обусловленности матрицы A:
В системе (1) изменим b на Δb. Тогда имеем:
Из (1) и (7) следует A·Δx=Δb. Тогда, учитывая (4) и (5) получим следующие неравенства:
Следовательно при q≠0 имеем:
При относительном изменении правой части 


Если q=0, то cond(A)=+∞, т.е. матрица неполного ранга (вырожденная). Чем больше cond(A), тем ближе матрица A к неполному рангу (к вырожденности). Чем ближе матрица к единичной матрице, тем больше cond(A) близка к 1 и , следовательно, матрица далека от неполного ранга (далека от вырожденности).
Свойства числа обусловленности матрицы:
- cond(A)>=1 (т.к. Q>=q).
- cond(P)=1, где P-матрица перестановок или единичная матрица.
- cond(λA)=cond(A), где λ скаляр.
, где D диагональная матрица.
Свойства 3 и 4 показывают, что cond(A) является лучшей критерией оценки вырожденности квадратных матриц, чем определитель. Действительно, если взять в качестве матрицы A квадратную диагональную матрицу 100×100 с элементами 0.1 на главной диагонали, то det(A)=(0.1) 100 =10 -100 , что очень малое число и показывает близость к вырожденности в то время, как строки и столбцы матрицы ортогональны и, в действительности матрица далека от вырожденности. Если же применять cond, то получим cond(A)=1.
Следующий пример иллюстрирует понятие числа обусловленности матрицы. Рассмотрим систему линейных уравнений (1), где
Тогда решением системы линейных уравнений будет 


Из (13) видно, что очень малое изменение в b, совершенно изменил решение x. Так как
Неравенство (15) показывает что матрица A плохо обусловлена, т.е. близка к вырожденности. С помощью экспериментальных вычислений мы обнаружили плохую обусловленность матрицы A. А как, на самом деле, вычислить число обусловленности матрицы. В выражении (4) Q называется нормой матрицы и ее можно вычислить с помощью следующего вырaжения:
где aj — j-ый столбец матрицы A. Оказывается, что 1/q является нормой обратной к A (если существует) матрицы A -1 : 
Вы можете вычислить обусловленность матрицы используя матричный онлайн калькулятор. Для этого вычислите обратную к матрице A, вычислите нормы для матриц A и A -1 и, используя выражение (17), вычислите cond(A).
Видео:Решение системы уравнений методом ГауссаСкачать

Обусловленность систем линейных уравнений
Две на первый взгляд похожие системы линейных уравнений могут обладать различной чувствительностью к погрешностям задания входных данных. Это свойство связано с понятием обусловленности системы уравнений.
Числом обусловленности линейного оператора A, действующего в нормированном пространстве 
Таким образом, появляется связь числа обусловленности с выбором нормы.
Предположим, что матрица и правая часть системы заданы неточно. При этом погрешность матрицы составляет dA, а правой части — dу. Можно показать, что для погрешности dx имеет место следующая оценка ( 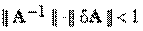

В частности, если dA = 0, то
При этом решение уравнения Ax = у не при всех у одинаково чувствительно к возмущению dу правой части.
Свойства числа обусловленности линейного оператора:
1.
причем максимум и минимум берутся для всех таких x, что 
2.
3
где 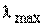
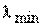
4.
Матрицы с большим числом обусловленности (ориентировочно 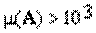
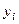
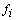
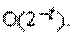
Таким образом, погрешность решения, вызванная погрешностями округления, может быть недопустимо большой в случае плохо обусловленных систем.
Итак – принципиально остаются две проблемы –
1.не обеспечивается обоснованная сходимость алгоритма к единственной (в случае модельного примера- истинной) структуре и
2. Не разрешено противоречие о неадекватности моделей шаговой регрессии на новых точках, не участвовавших при оценке параметров модели. Возможно ли, если не обеспечить такую адекватность при других способах синтеза моделей, то хотя бы найти путь к решению такой задачи (возможно и адекватность определить другим способом )
Для АШР даже в случае применения для МНК оценки процедуры Грамма-Шмидта не разрешается вопрос о единственности модели – просто оценки параметров становятся наиболее точными и несмещенными
Т.о. гарантированное нахождение всего множества подходящих решений в реальных задачах (при 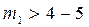
перебора всех подструктур полной структуры как в методе всех регрессий (у Дрейпера и Смита). Тогда мы найдем всете модели, в которых все аргументы входят с уровнем значимости не менее чем заданный. Со всеми выше описанными проблемами – а какая же из них, из этого множества та, которая действительно наша.
Можно еще добавить камень в огород АШР о неиспользуемой возможности вариации уровнем значимости для учета уровня шума в данных
Именно эту проблему предлагает решать МГУА с помощью введения понятия внешних критериев.
Необходимое примечание.
при 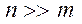
Каждый из них это делает по своему, и определить адекватность метода по сходимости к нужной модели можно только построив соответствующий вашей задаче модельный пример.
Однако наиболее распространенный случай – это когда число точек невелико 
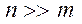
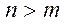


И наиболее эффективный подход к решению структурно-параметрического синтеза при данных условиях демонстрирует МГУА
Как видим нарушение уже первого условия порождаетнеобходимомость разрешения проблемы множественности моделей не прибегая к процедуре полного перебора –надо предложить какой-то принцип, позволяющий найти путь к истинной или квазиистинной модели без полного перебора претендентов моделей.
Следующая проблема не менее реальна и еще более запутывает задачу поиска структуры. – проблема шума в данных –мы помним что при это нарушаются свойства проекционности аппарата МНК – нарушаются свойства оценок, но проблема в том что на зашумленных данных найти истинную структуру вообще может бытььпроблематично – если неизвестны х-ки шума и точки их приложения алгоритм будет тупо подстраиваться под шум.
Основная проблема– проблема необоснованности выбора структуры модели классическими АШГ многократно обостряется в связи с тем что порог используемый критерием Фишера в виде уровня значимости
на самом деле регулирует не только риск ошибки
– его выбор должен учитывать уровень шума и точки его приложения.
Ведь увеличение уровня шума например на выходе неизбено требует загрубить модель (не подстраивать ее под шум) а значит изменить уровень увеличить значимости с тем чтобы более жестко фильтровать апгументы в модель и ее упрощать .
Гораздо сложнее учесть шумы на входе тем более если они проходят нелинейное преобразование модели.
Однако методологически механизмов учета данных коррекций в агоритмах нет что делает выбор структур в условиях шума необоснованным.
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

6.1. Решение систем линейных алгебраических уравнений. Обусловленность матрицы
При исследовании численных методов для решения математических задач необходимо различать свойства самой задачи и свойства вычислительного алгоритма. Для каждой математической задачи принято рассматривать вопрос о ее корректности.
Определение. Говорят, что задача поставлена корректно, если ее решение существует, единственно и непрерывно зависит от входных данных.
Где А — квадратная, неособенная матрица размерности N, и, следовательно, det(A) ≠ 0, тогда существует единственное решение системы. Чтобы убедиться в корректности задачи (6.1) необходимо еще установить непрерывную зависимость решения от входных данных. Входными данными являются правая часть F и элементы матрицы А.
Соответственно, различают устойчивость по правой части, когда возмущается только правая часть F , а матрица А остается неизменной, и коэффициентную устойчивость, когда возмущается только матрица А .
Будем считать, что решение и правая часть задачи (6.1) принадлежат линейному пространству H, состоящему из N-мерных векторов. Введем в H норму, для которой выполнено:
||X||>0, для всех Х≠0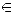
||α X||=| α| ||X||, для любого числа А и Х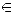
||X+Y||≤||X||+||Y||, для любых X и Y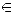
Определение. Нормой матрицы А, подчиненной данной норме векторов, называется число 
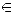
Наряду с системой (6.1) рассмотрим «возмущенную» систему A Xε = Fδ , которая отличается от (6.1) правой частью. Насколько сильно может измениться решение Х В результате изменения правой части?
Определение. Говорят, что система (6.1) устойчива по правой части, если при любых F и Fδ Справедлива оценка || δx||≤ M || δf ||, где M — постоянная, M >0.
Эта оценка выражает факт непрерывной зависимости решения от правой части, то есть показывает, что || δx|| Стремится к нулю при || δf ||Стремящемся к нулю. Наличие устойчивости очень важно при численном решении систем уравнений, так как никогда нельзя задать правую часть F точно. Погрешность δf возникает в результате округления.
Получим оценку для относительной погрешности решения 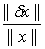
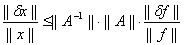
Определение. Число ρ(A)= 
ρ(A)=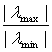
Где λMax , λmin – максимальное и минимальное по модулю собственные значения матрицы A.
Матрицы с большим числом обусловленности называются плохо обусловленными. При численном решении систем с такими матрицами возможно сильное накопление погрешности. При небольших изменениях правой части погрешность решения может оказаться значительной.
Например, для матрицы
Число обусловленности ρ(A)=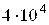
Если взять матрицу
И за правую часть системы вектор F= (1,0000, 0)T, то получим решение 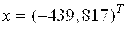
📺 Видео
Матричный метод решения систем уравненийСкачать

Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Линейная алгебра, 7 урок, СЛАУ. Матричный методСкачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

12 Обусловленность и устойчивостьСкачать

Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

Ефимов В.А. "Что за перевалом СВО. Смыслы будущего"Скачать

"Неудобные вопросы" Девятов А.П. 2024-01-24Скачать

Лекция 3, Число обусловленности, диагональное преобладаниеСкачать

Метод Гаусса решения систем линейных уравненийСкачать

Линейная алгебра, Матрицы: Метод Гаусса. Высшая математикаСкачать

Линейная алгебра: матрицы, определители, метод Крамера. Высшая математикаСкачать

Матрица интенсивностей. Система уравнений КолмогороваСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Решение систем линейных уравнений с помощью матрицСкачать

Решение системы линейных уравнений методом ГауссаСкачать













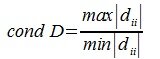 , где D диагональная матрица.
, где D диагональная матрица.