Общий перпендикуляр к двум скрещивающимся прямым уравнение

Видео:Построение общего перпендикуляра к двум скрещивающимся прямым | Стереометрия #33 | ИнфоурокСкачать

Общий перпендикуляр к двум скрещивающимся прямым. Расстояние между скрещивающимися прямыми

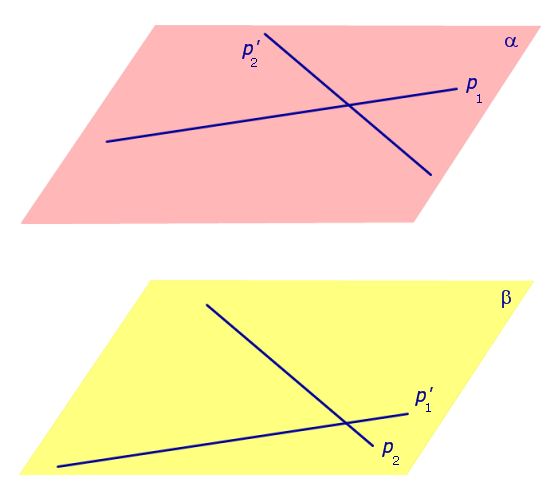
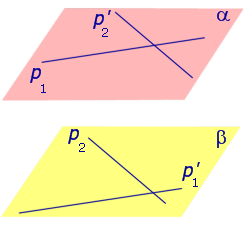
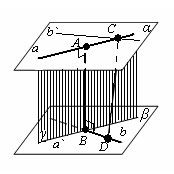
Теорема. Пусть p₁ и p₂ – две произвольные скрещивающиеся прямые скрещивающиеся прямые . Если рассмотреть всевозможные прямые A₁A₂, такие, что точка A₁ лежит на прямой p₁, а точка A₂ лежит на прямой p₂, то будут выполнены следующие два утверждения:

1. Среди всех прямых A₁A₂ существует единственная прямая, перпендикулярная к прямой p₁ и к прямой p₂ ( общий перпендикуляр к двум скрещивающимся прямым ).
2. Среди всех отрезков A₁A₂наименьшую длину имеет отрезок общего перпендикуляра к двум скрещивающимся прямым.

Доказательство. Докажем сначала существование общего перпендикуляра к двум скрещивающимся прямым.

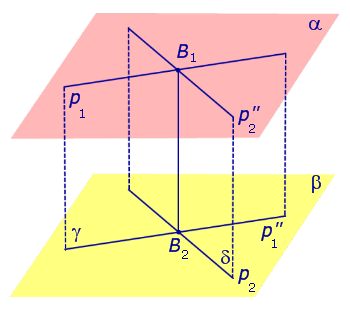
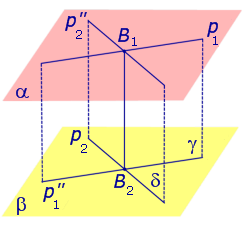
Через произвольную точку прямой p₁ проведем прямую , параллельную прямой параллельную прямой p₂ , а через произвольную точку прямой p₂ проведем прямую , параллельную прямой параллельную прямой p₁ . Обозначим буквой α плоскость, проходящую через прямые p₁ и , а буквой β плоскость, проходящую через прямые p₂ и (рис 1).

Поскольку прямая p₁ параллельна прямой , лежащей на плоскости β , то по признаку параллельности прямой и плоскости прямая p₁ параллельна плоскости β. Точно так же, поскольку прямая параллельна прямой p₂ , лежащей на плоскости β , то прямая по признаку параллельности прямой и плоскости параллельна плоскости β. Таким образом, плоскость α содержит две пересекающиеся прямые p₁ и , паралельные плоскости β. В силу признака параллельности плоскостей заключаем, что плоскости α и β параллельны.

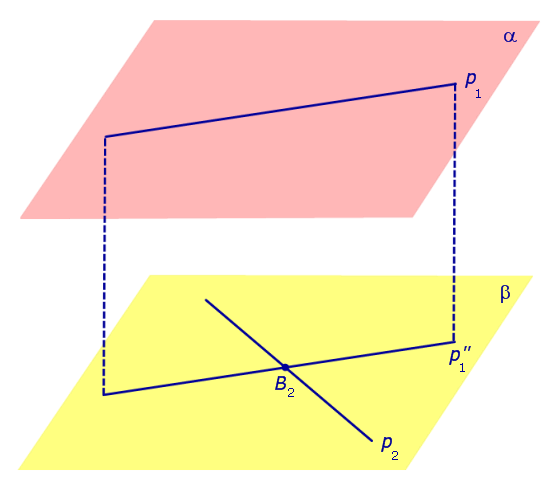
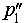
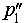
Спроектируем прямую p₁ на плоскость β. Получим прямую , являющуюся проекцией прямой проекцией прямой p₁, и обозначим точку пересечения прямых p₂ и буквой B₂ (рис. 2).

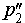
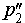
Спроектируем теперь прямую p₂ на плоскость α . Получим прямую , являющуюся проекцией прямой проекцией прямой p₂ , и обозначим точку пересечения прямых p₁ и буквой B₁ (рис. 3).

Доказательство существования общего перпендикуляра к двум скрещивающимся прямым завершено.

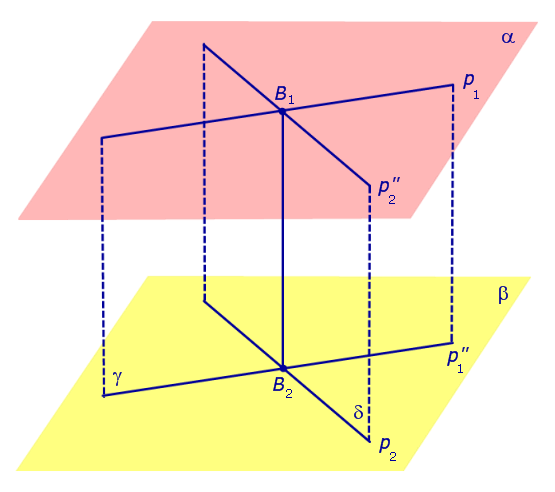
Докажем, что построенная прямая B₁B₂ является единственным общим перпендикуляром к прямым p₁ и p₂ .

Таким образом, общий перпендикуляр к прямым p₁ и p₂ является линией пересечения плоскостей γ и δ, то есть прямой B₁B₂ .

Доказательство единственности общего перпендикуляра к двум скрещивающимся прямым завершено. Утверждение 1 доказано.

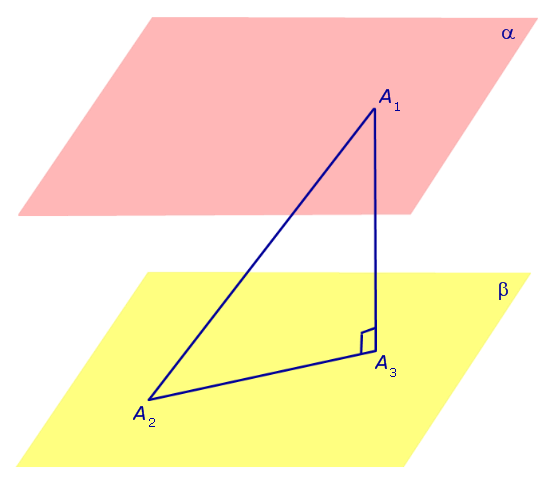
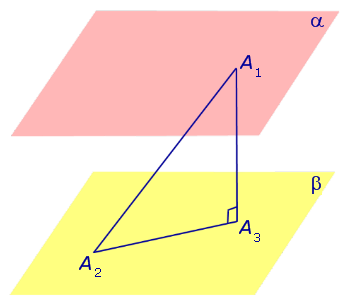
Перейдем к доказательству утверждения 2. Для этого рассмотрим произвольный отрезок A₁A₂ , у которого конец A₁ лежит на плоскости α , а конец A₂ лежит на плоскости β . Опустим перпендикуляр из точки A₁ на плоскость β и обозначим основание этого перпендикуляра символом A₃ (рис. 4).

Если отрезок A₁A₂ не является перпендикуляром к плоскостям α и β, то точка A₃ не совпадет с точкой A₂ , и треугольник A₁A₂A₃ будет прямоугольным треугольником с гипотенузой A₁A₂ и катетом A₁A₃. Поскольку в прямоугольном треугольнике длина катета меньше длины гипотенузы, то

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

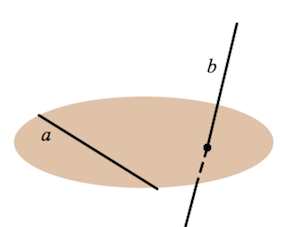
Скрещивающиеся прямые

Скрещивающиеся прямые – прямые, которые невозможно поместить в одну плоскость, то есть они не параллельны и не пересекаются.

Видео:Расстояние между скрещивающимися прямыми и уравнение их общего перпендикуляра.Скачать

Признак скрещивающихся прямых

Если одна из прямых лежит в плоскости, а вторая пересекает эту плоскость в точке, отличной от точек первой прямой, то такие прямые – скрещивающиеся .

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

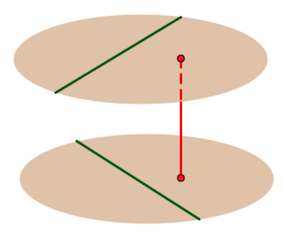
Расстояние между скрещивающимися прямыми

Через две скрещивающиеся прямые можно провести две параллельные плоскости (единственным образом).

Расстояние между скрещивающимися прямыми – есть расстояние между этими плоскостями.

Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

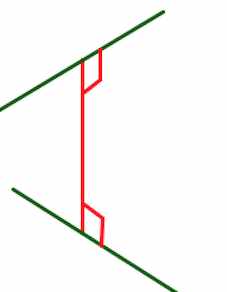
Общий перпендикуляр к двум скрещивающимся прямым

Общим перпендикуляром к двум скрещивающимся прямым называется отрезок, перпендикулярный каждой из двух скрещивающихся прямых, концы которого лежат на этих прямых.

Длина общего перпендикуляра равна расстоянию между скрещивающимися прямыми.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Угол между скрещивающимися прямыми

Углом между двумя скрещивающимися прямыми называется угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.

(Одну из прямых можно вполне и не переносить параллельно самой себе, а ограничиться только параллельным переносом одной из прямых до пересечения со второй).

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

Общий перпендикуляр к двум скрещивающимся прямым уравнение

Признак

a α, b α = A , A a (чертеж 2.1.2). Допустим, что прямые a и b не скрещивающиеся, то есть они пересекаются. Тогда существует плоскость β, которой принадлежат прямые a и b . В этой плоскости β лежат прямая a и точка A . Поскольку прямая a и точка A вне ее определяют единственную плоскость, то β = α. Но b β и b α, следовательно, равенство β = α невозможно.

Теорема

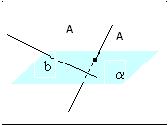
Две скрещивающиеся прямые имеют общий перпендикуляр, и при том только один. Он является общим перпендикуляром параллельных плоскостей, проходящих через эти прямые.

Доказательство

Пусть a и b – данные скрещивающиеся прямые. Проведем через них параллельные плоскости α и β. Прямые, пересекающие прямую a и перпендикулярные плоскости α, лежат в одной плоскости (γ). Эта плоскость пересекает плоскость β по прямой a`, параллельной a. Пусть B – точка пересечения прямых a` и b. Тогда прямая AB, перпендикулярная плоскости α, перпендикулярна и плоскости β, так как β параллельна α. Отрезок AB – общий перпендикуляр плоскостей α и β, а значит, и прямых a и b.
Докажем, что этот общий перпендикуляр единственный. Допустим, что у прямых a и b есть другой общий перпендикуляр CD. Проведем через точку С прямую b`, параллельную b. Прямая CD перпендикулярна прямой b, а значит, и b`. Так как она перпендикулярна прямой a, то она перпендикулярна плоскости α, а значит, параллельна прямой AB. Выходит, что через прямые AB и CD, как через параллельные, можно провести плоскость. В этой плоскости будут лежать наши скрещивающиеся прямые AC и BD, а это невозможно, что и требовалось доказать.

Расстоянием между двумя скрещивающимися прямыми называется длина их общего перпендикуляра.

📽️ Видео

✓ Расстояние между скрещивающимися прямыми | ЕГЭ-2018. Задание 13. Математика | Борис ТрушинСкачать

Расстояние между скрещивающимися прямыми #2Скачать

10 класс, 7 урок, Скрещивающиеся прямыеСкачать

Расстояние между скрещивающимися прямымиСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

#31. Как найти расстояние между скрещивающимися прямыми?Скачать

11. Прямая в пространстве и ее уравненияСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

найти уравнения биссектрис углов между прямымиСкачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Общий перпендикуляр к двум прямымСкачать

Теорема о трёх перпендикулярах | Ботай со мной #032 | Борис Трушин |Скачать