Общий перпендикуляр двух скрещивающихся прямых уравнение

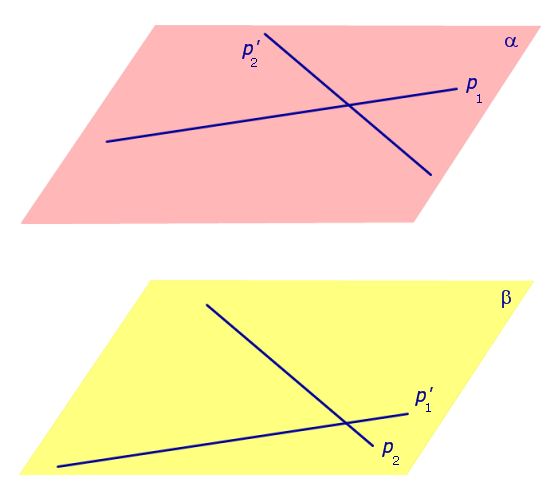
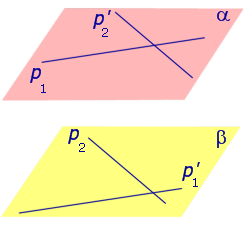
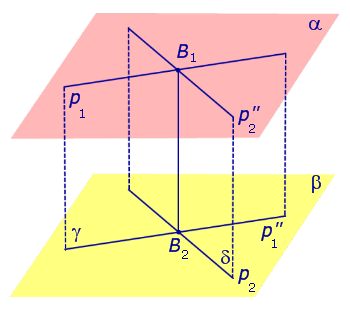
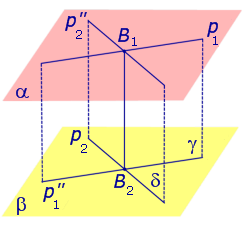
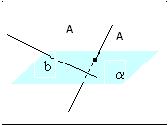
Теорема. Пусть p₁ и p₂ – две произвольные скрещивающиеся прямые скрещивающиеся прямые . Если рассмотреть всевозможные прямые A₁A₂, такие, что точка A₁ лежит на прямой p₁, а точка A₂ лежит на прямой p₂, то будут выполнены следующие два утверждения:

1. Среди всех прямых A₁A₂ существует единственная прямая, перпендикулярная к прямой p₁ и к прямой p₂ ( общий перпендикуляр к двум скрещивающимся прямым ).
2. Среди всех отрезков A₁A₂наименьшую длину имеет отрезок общего перпендикуляра к двум скрещивающимся прямым.

Доказательство. Докажем сначала существование общего перпендикуляра к двум скрещивающимся прямым.

Через произвольную точку прямой p₁ проведем прямую , параллельную прямой параллельную прямой p₂ , а через произвольную точку прямой p₂ проведем прямую , параллельную прямой параллельную прямой p₁ . Обозначим буквой α плоскость, проходящую через прямые p₁ и , а буквой β плоскость, проходящую через прямые p₂ и (рис 1).

Поскольку прямая p₁ параллельна прямой , лежащей на плоскости β , то по признаку параллельности прямой и плоскости прямая p₁ параллельна плоскости β. Точно так же, поскольку прямая параллельна прямой p₂ , лежащей на плоскости β , то прямая по признаку параллельности прямой и плоскости параллельна плоскости β. Таким образом, плоскость α содержит две пересекающиеся прямые p₁ и , паралельные плоскости β. В силу признака параллельности плоскостей заключаем, что плоскости α и β параллельны.

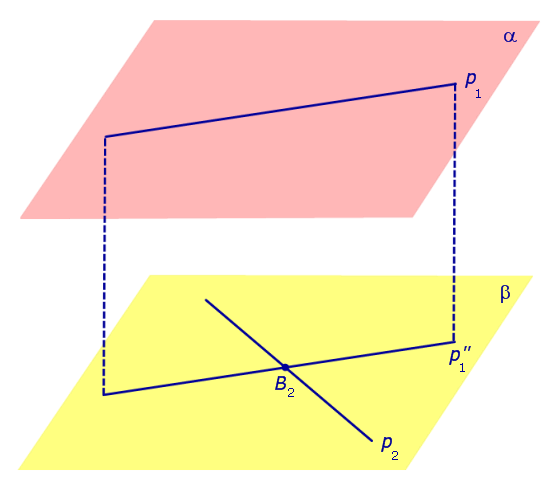
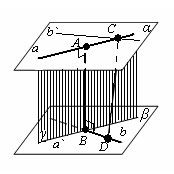
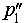
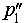
Спроектируем прямую p₁ на плоскость β. Получим прямую , являющуюся проекцией прямой проекцией прямой p₁, и обозначим точку пересечения прямых p₂ и буквой B₂ (рис. 2).

Спроектируем теперь прямую p₂ на плоскость α . Получим прямую 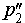, являющуюся проекцией прямой проекцией прямой p₂ , и обозначим точку пересечения прямых p₁ и буквой B₁ (рис. 3).

Доказательство существования общего перпендикуляра к двум скрещивающимся прямым завершено.

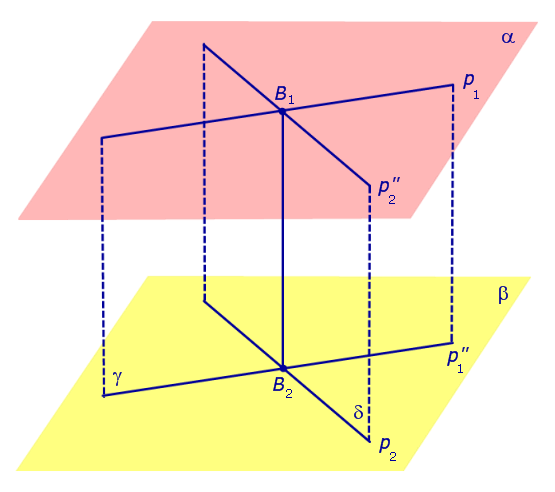
Докажем, что построенная прямая B₁B₂ является единственным общим перпендикуляром к прямым p₁ и p₂ .

Таким образом, общий перпендикуляр к прямым p₁ и p₂ является линией пересечения плоскостей γ и δ, то есть прямой B₁B₂ .

Доказательство единственности общего перпендикуляра к двум скрещивающимся прямым завершено. Утверждение 1 доказано.

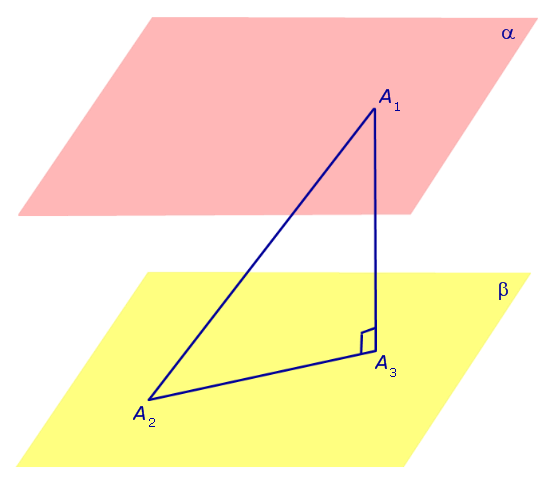
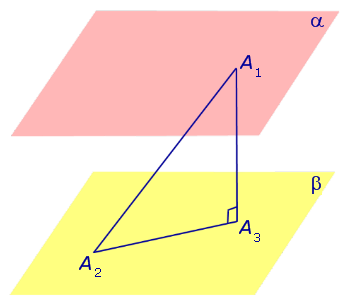
Перейдем к доказательству утверждения 2. Для этого рассмотрим произвольный отрезок A₁A₂ , у которого конец A₁ лежит на плоскости α , а конец A₂ лежит на плоскости β . Опустим перпендикуляр из точки A₁ на плоскость β и обозначим основание этого перпендикуляра символом A₃ (рис. 4).

Если отрезок A₁A₂ не является перпендикуляром к плоскостям α и β, то точка A₃ не совпадет с точкой A₂ , и треугольник A₁A₂A₃ будет прямоугольным треугольником с гипотенузой A₁A₂ и катетом A₁A₃. Поскольку в прямоугольном треугольнике длина катета меньше длины гипотенузы, то

Видео:Построение общего перпендикуляра к двум скрещивающимся прямым | Стереометрия #33 | ИнфоурокСкачать

Четыре способа решения задач на нахождение расстояния между скрещивающимися прямыми

Разделы: Математика

Среди огромного количества стереометрических задач в учебниках геометрии, в различных сборниках задач, пособиях по подготовке в ВУЗы крайне редко встречаются задачи на нахождение расстояния между скрещивающимися прямыми. Возможно, это обусловлено как узостью их практического применения (относительно школьной программы, в отличие от «выигрышных» задач на вычисление площадей и объемов), так и сложностью данной темы.

Практика проведения ЕГЭ показывает, что многие учащиеся вообще не приступают к выполнению заданий по геометрии, входящих в экзаменационную работу. Для обеспечения успешного выполнения геометрических заданий повышенного уровня сложности необходимо развивать гибкость мышления, способность анализировать предполагаемую конфигурацию и вычленять в ней части, рассмотрение которых позволяет найти путь решения задачи.

Школьный курс предполагает изучение четырех способов решения задач на нахождение расстояния между скрещивающимися прямыми. Выбор способа обусловлен, в первую очередь, особенностями конкретной задачи, предоставленными ею возможностями для выбора, и, во вторую очередь, способностями и особенностями «пространственного мышления» конкретного учащегося. Каждый из этих способов позволяет решить самую главную часть задачи — построение отрезка, перпендикулярного обеим скрещивающимся прямым (для вычислительной же части задач деление на способы не требуется).

Основные способы решения задач на нахождение расстояния между скрещивающимися прямыми

Нахождение длины общего перпендикуляра двух скрещивающихся прямых, т.е. отрезка с концами на этих прямых и перпендикулярного каждой из этих прямых.

Нахождение расстояния от одной из скрещивающихся прямых до параллельной ей плоскости, проходящей через другую прямую.

Нахождение расстояния между двумя параллельными плоскостями, проходящими через заданные скрещивающиеся прямые.

Нахождение расстояния от точки, являющейся проекцией одной из скрещивающихся прямых, на перпендикулярную ей плоскость (так называемый «экран») до проекции другой прямой на ту же самую плоскость.

Проведем демонстрацию всех четырех способов на следующей простейшей задаче: «В кубе с ребром а найти расстояние между любым ребром и диагональю не пересекающей его грани». Ответ: .

h_скр перпендикулярна плоскости боковой грани, содержащей диагональ d и перпендикулярна ребру, следовательно, h_скр и является расстоянием между ребром а и диагональю d.

Плоскость A параллельна ребру и проходит через данную диагональ, следовательно, данная h_скр является не только расстоянием от ребра до плоскости A, но и расстоянием от ребра до данной диагонали.

Плоскости A и B параллельны и проходят через две данные скрещивающиеся прямые, следовательно, расстояние между этими плоскостями равно расстоянию между двумя скрещивающимися прямыми.

Плоскость A перпендикулярна ребру куба. При проекции на A диагонали d данная диагональ обращается в одну из сторон основания куба. Данная h_скр является расстоянием между прямой, содержащей ребро, и проекцией диагонали на плоскость C, а значит и между прямой, содержащей ребро, и диагональю.

Остановимся подробнее на применении каждого способа для изучаемых в школе многогранников.

Применение первого способа достаточно ограничено: он хорошо применяется лишь в некоторых задачах, так как достаточно сложно определить и обосновать в простейших задачах точное, а в сложных — ориентировочное местоположение общего перпендикуляра двух скрещивающихся прямых. Кроме того, при нахождении длины этого перпендикуляра в сложных задачах можно столкнуться с непреодолимыми трудностями.

Задача 1. В прямоугольном параллелепипеде с размерами a, b, h найти расстояние между боковым ребром и не пересекающейся с ним диагональю основания.

Пусть AHBD. Так как А₁А перпендикулярна плоскости АВСD , то А₁А AH.

AH перпендикулярна обеим из двух скрещивающихся прямых, следовательно AH?- расстояние между прямыми А₁А и BD. В прямоугольном треугольнике ABD, зная длины катетов AB и AD, находим высоту AH, используя формулы для вычисления площади прямоугольного треугольника. Ответ:

Задача 2. В правильной 4-угольной пирамиде с боковым ребром L и стороной основания a найти расстояние между апофемой и стороной основания, пересекающей боковую грань, содержащую эту апофему.

SHCD как апофема, ADCD, так как ABCD — квадрат. Следовательно, DH — расстояние между прямыми SH и AD. DH равно половине стороны CD. Ответ:

Применение этого способа также ограничено в связи с тем, что если можно быстро построить (или найти уже готовую) проходящую через одну из скрещивающихся прямых плоскость, параллельную другой прямой, то затем построение перпендикуляра из любой точки второй прямой к этой плоскости (внутри многогранника) вызывает трудности. Однако в несложных задачах, где построение (или отыскивание) указанного перпендикуляра трудностей не вызывает, данный способ является самым быстрым и легким, и поэтому доступен.

Задача 2. Решение уже указанной выше задачи данным способом особых трудностей не вызывает.

Плоскость EFM параллельна прямой AD, т. к AD || EF. Прямая MF лежит в этой плоскости, следовательно, расстояние между прямой AD и плоскостью EFM равно расстоянию между прямой AD и прямой MF. Проведем OHAD. OHEF, OHMO, следовательно, OH(EFM), следовательно, OH — расстояние между прямой AD и плоскостью EFM, а значит, и расстояние между прямой AD и прямой MF. Находим OH из треугольника AOD.

Ответ:

Задача 3. В прямоугольном параллелепипеде с размерами a,b и h найти расстояние между боковым ребром и не пересекающейся с ним диагональю параллелепипеда.

Прямая AA₁ параллельна плоскости BB₁D₁D, B₁D принадлежит этой плоскости, следовательно расстояние от AA₁ до плоскости BB₁D₁D равно расстоянию между прямыми AA₁ и B₁D. Проведем AHBD. Также, AH B₁B, следовательно AH(BB₁D₁D), следовательно AHB₁D, т. е. AH — искомое расстояние. Находим AH из прямоугольного треугольника ABD.

Ответ:

Задача 4. В правильной шестиугольной призме A:F₁ c высотой h и стороной основания a найти расстояние между прямыми:

Рассмотрим плоскость E₁EDD₁. A₁E₁EE₁, A₁E₁E₁D₁, следовательно

A₁E₁ (E₁EDD₁). Также A₁E₁ AA₁. Следовательно, A₁E₁ является расстоянием от прямой AA₁ до плоскости E₁EDD₁. ED₁(E₁EDD₁)., следовательно AE₁ — расстояние от прямой AA₁ до прямой ED₁. Находим A₁E₁ из треугольника F₁A₁E₁ по теореме косинусов. Ответ:

б) AF и диагональю BE₁.

Проведем из точки F прямую FH перпендикулярно BE. EE₁FH, FHBE, следовательно FH(BEE₁B₁), следовательно FH является расстоянием между прямой AF и (BEE₁B₁), а значит и расстоянием между прямой AF и диагональю BE₁. Ответ:

Применение этого способа крайне ограничено, так как плоскость, параллельную одной из прямых (способ II) строить легче, чем две параллельные плоскости, однако способ III можно использовать в призмах, если скрещивающиеся прямые принадлежат параллельным граням, а также в тех случаях, когда в многограннике несложно построить параллельные сечения, содержащие заданные прямые.

а) Плоскости BAA₁B₁ и DEE₁D₁ параллельны, так как AB || ED и AA₁ || EE₁. ED₁DEE₁D₁, AA₁(BAA₁B₁), следовательно, расстояние между прямыми AA₁ и ED₁ равно расстоянию между плоскостями BAA₁B₁ и DEE₁D₁. A₁E₁AA₁, A₁E₁A₁B₁, следовательно, A₁E₁BAA₁B₁. Аналогично доказываем, что A₁E₁(DEE₁D₁). Т.о., A₁E₁ является расстоянием между плоскостями BAA₁B₁ и DEE₁D₁, а значит, и между прямыми AA₁ и ED₁. Находим A₁E₁ из треугольника A₁F₁E₁, который является равнобедренным с углом A₁F₁E₁, равным . Ответ:

б) Расстояние между AF и диагональю BE₁ находится аналогично.

Ответ:.

Задача 5. В кубе с ребром а найти расстояние между двумя непересекающимися диагоналями двух смежных граней.

Данная задача рассматривается как классическая в некоторых пособиях, но, как правило, ее решение дается способом IV, однако является вполне доступной для решения с помощью способа III.

Некоторую трудность в данной задаче вызывает доказательство перпендикулярности диагонали A₁C обеим параллельным плоскостям (AB₁D₁ || BC₁D). B₁CBC₁ и BC₁A₁B₁, следовательно, прямая BC₁ перпендикулярна плоскости A₁B₁C, и следовательно, BC₁A₁C. Также, A₁CBD. Следовательно, прямая A₁C перпендикулярна плоскости BC₁D. Вычислительная же часть задачи особых трудностей не вызывает, так как h_скр = EF находится как разность между диагональю куба и высотами двух одинаковых правильных пирамид A₁AB₁D₁ и CC₁BD.

Ответ:

Данный способ имеет достаточно широкое применение. Для задач средней и повышенной трудности его можно считать основным. Нет необходимости применять его только тогда, когда один из трех предыдущих способов работает проще и быстрее, так как в таких случаях способ IV может только усложнить решение задачи, или сделать его труднодоступным. Данный способ очень выгодно использовать в случае перпендикулярности скрещивающихся прямых, так как нет необходимости построения проекции одной из прямых на «экран»

Задача 5. Все та же «классическая» задача (с непересекающимися диагоналями двух смежных граней куба) перестает казаться сложной, как только находится «экран» — диагональное сечение куба.

Рассмотрим плоскость A₁B₁CD. C₁F (A₁B₁CD), т. к. C₁FB₁C и C₁FA₁B₁. Тогда проекцией C₁D на «экран» будет являться отрезок DF. Проведем EMDF. Отрезок EM и будет являться расстоянием между двумя непересекающимися диагоналями двух смежных граней. Находим EM из прямоугольного треугольника EDF. Ответ:.

Задача 6. В правильной треугольной пирамиде найти расстояние и угол между скрещивающимися прямыми: боковым ребром l и стороной основания a.

В данной и аналогичных ей задачах способ IV быстрее других способов приводит к решению, так как построив сечение, играющее роль «экрана», перпендикулярно AC (треугольник BDM), видно, что далее нет необходимости строить проекцию другой прямой (BM) на этот экран. DH — искомое расстояние. DH находим из треугольника MDB, используя формулы площади. Ответ: .

Видео:Расстояние между скрещивающимися прямыми и уравнение их общего перпендикуляра.Скачать

Общий перпендикуляр двух скрещивающихся прямых уравнение

Признак

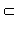
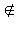
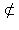
a α, b α = A , A a (чертеж 2.1.2). Допустим, что прямые a и b не скрещивающиеся, то есть они пересекаются. Тогда существует плоскость β, которой принадлежат прямые a и b . В этой плоскости β лежат прямая a и точка A . Поскольку прямая a и точка A вне ее определяют единственную плоскость, то β = α. Но b β и b α, следовательно, равенство β = α невозможно.

Теорема

Две скрещивающиеся прямые имеют общий перпендикуляр, и при том только один. Он является общим перпендикуляром параллельных плоскостей, проходящих через эти прямые.

Доказательство

Пусть a и b – данные скрещивающиеся прямые. Проведем через них параллельные плоскости α и β. Прямые, пересекающие прямую a и перпендикулярные плоскости α, лежат в одной плоскости (γ). Эта плоскость пересекает плоскость β по прямой a`, параллельной a. Пусть B – точка пересечения прямых a` и b. Тогда прямая AB, перпендикулярная плоскости α, перпендикулярна и плоскости β, так как β параллельна α. Отрезок AB – общий перпендикуляр плоскостей α и β, а значит, и прямых a и b.
Докажем, что этот общий перпендикуляр единственный. Допустим, что у прямых a и b есть другой общий перпендикуляр CD. Проведем через точку С прямую b`, параллельную b. Прямая CD перпендикулярна прямой b, а значит, и b`. Так как она перпендикулярна прямой a, то она перпендикулярна плоскости α, а значит, параллельна прямой AB. Выходит, что через прямые AB и CD, как через параллельные, можно провести плоскость. В этой плоскости будут лежать наши скрещивающиеся прямые AC и BD, а это невозможно, что и требовалось доказать.

Расстоянием между двумя скрещивающимися прямыми называется длина их общего перпендикуляра.

🎬 Видео

10 класс, 7 урок, Скрещивающиеся прямыеСкачать

19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

Взаимное расположение прямых в пространстве. 10 класс.Скачать

✓ Расстояние между скрещивающимися прямыми | ЕГЭ-2018. Задание 13. Математика | Борис ТрушинСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Расстояние между скрещивающимися прямымиСкачать

10 класс - Геометрия - Скрещивающиеся прямыеСкачать

Параллельные прямые | Математика | TutorOnlineСкачать

Угол между прямыми в пространстве. 10 класс.Скачать

Расстояние между скрещивающимися прямыми #2Скачать

7. Скрещивающиеся прямыеСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Скрещивающиеся прямыеСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

ЕГЭ задание 13 Расстояние между скрещивающимися прямымиСкачать

Урок 15. Все способы расстояние между скрещивающимися прямыми. Стереометрия с нуля.Скачать

Определение кратчайшего расстояние между скрещивающимися прямыми методом замены плоскостей проекцииСкачать