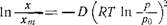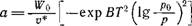Общий алгоритм построения распределения пор по размерам на основе уравнения кельвина (4 видео)

Лако-красочные материалы — производство

Содержание

Технологии и оборудование для изготовления красок, ЛКМ
Теория капиллярной конденсации. Распределение пор по размерам
Адсорбция и адсобционные равновесия
Размер пор и распределение пор по размерам
📸 Видео

Видео:Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

Технологии и оборудование для изготовления красок, ЛКМ

Видео:Математика. Линейные диофантовы уравнения с двумя неизвестными. Центр онлайн-обучения «Фоксфорд»Скачать

Теория капиллярной конденсации. Распределение пор по размерам

Удерживание газов и паров пористыми телами, т. е. их адсорбционная способность, зависят как от природы взаимодействующих тел, так и от структуры пористого тела. Если структурный фактор для макропористых адсорбентов имеет малое значение, то уже для переходнопористых тел его роль резко возрастает. Это обусловлено в первую очередь проявлением капиллярных сил, действие которых с ростом дисперсности тела непосредственно связано со сродством адсорбата к адсорбенту. Основываясь на закономерностях капиллярных явлений, можно утверждать, что такое сродство должно быть достаточ
ным, чтобы поверхность пористого тела смачивалась жидкостью, появляющейся в результате конденсации пара в порах. Только при условии смачивания капиллярные силы будут втягивать адсорбат в поры и обеспечивать адсорбционную способность пористого тела. Чем меньше размер пор, тем сильнее капиллярное удерживание адсорбата. В противном случае (если поверхность не смачивается) наблюдается капиллярное выталкивание вещества из пор, адсорбция на несмачиваемы. ч телах минимальна и возможна только на ровной поверхности н в крупных порах.

Адсорбция на переходнопористых телах происходит в основном по механизму капиллярной конденсации. Капиллярная конденсация начинает проявляться при определенной степени заполнения адсорбента или при определенном значении давления пара, характерном для данной системы. К этому моменту поверхностная энергия адсорбента практически полностью скомпенсирована в результате полимолекулярной адсорбции, а микропоры заполнены адсорбатом. С увеличением давления газа или пара конденсация происходит и в более крупных порах, радиус мениска жидкости г в которых находится в соответствии с уравнением капиллярной конденсации Кельвина (отрицательная кривизна):

Из этого уравнения следует, что при смачивании, обеспечивающем отрицательную кривизну мениска конденсата (вогнутый мениск), конденсация в порах наступает при давлении, меньшем давления насыщенного пара, т. е. при Plps

Из которого следует, что адсорбционный потенциал в теории капиллярной конденсации принимается равным капиллярному потенциалу. В уравнении (III.73) связь адсорбционного потенциала со структурой и природой адсорбента выражается в виде простой (обратно пропорциональной) зависимости от радиуса мениска конденсата в порах. Остальные параметры, определяющие адсорбционный потенциал, относятся только к конденсату. Очевидно, что только при полном смачивании радиус мениска можно приравнять радиусу поры; в общем же случае тп = г cos В, где В — угол смачивания.

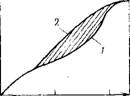
Для адсорбентов с переходными порами характерна изотерма адсорбции с петлей капиллярно-конденсационного гистерезиса (рис. III.11). Адсорбции соответствует нижняя кривая, а десорбции — верхняя. При малых давлениях, когда не происходит капиллярная конденсация, гистерезиса не наблюда-
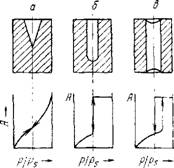
етс-я. Начало появления гистерезиса зависит от природы адсорбента и адсорбата. Пористая структура адсорбента разнообразна, однако считается, что ее можно смоделировать следующими тремя видами пор: конусообразными, цилиндрическими с одним открытым концом, и цилиндрическими с двумя открытыми концами (рис. III.12). Конденсация в конусообразных порах начинается со дна пор, где кривизна наибольшая. По мере заполнения поры радиус мениска увеличивается (уменьшается кривизна), поэтому дли дальнейшего заполнения поры необходимо увеличивать давление (рис. III.12 о). Процесс чесорбшш идет в обратном направлении и описывается той же кривой. В цилиндрических норах с одним открытым концом конденсация начинается также со дна пор, где кривизна сферическая и поэтому наибольшая (рис. 111.126). Так как пора цилиндрическая, то она заполняется целиком при определенном постоянном радиусе мениска, что отвечает и определенному постоянному давлению пара. Капиллярная конденсация в этих порах» также происходит обратимо. Йсли у цилиндрической поры тех же размеров оба конца открытые (рис. 1П.12в), то конденсация начнется на стенках цилиндра, имеющего кривизну в два раза меньше, чем у сферы того же радиуса. Поэтому заполнение поры происходит при большом давлении пара в соответствии с соотношением

Конденсация па стенках цилиндрической поры приводит к уменьшению диаметра поры, что вызывает ее мгновенное заполнение при давлении, отвечающем началу конденсации. На концах поры образуются сферические мениски жидкости. Десорбция может начаться только при давлении, соответствующем радиусам кривизны этих менисков, т. е. определяемых уравнением (III.72). Таким образом, опорожнение капилляра происходит при меньшем давлении, чем его заполнение. Этим объясняется появление петли капиллярно-конденсационного гистерезиса. Так как реальные адсорбенты имеют поры различных форм и размеров, которые заполняются и опорожня-

Ются при разных давлениях, то реальные изотермы адсорбции имеют вид, показанный на рис. III.11. После рассмотренного примера легко представить появление гистерезиса в бутылочных порах (порах с узким выходом).

Рис. II 1.11. Изотерма адсорбции при капиллярной конденсации:

1 — кривая адсорбции: 2— кривая десорбции

Рис. 111.12. Виды пор и соответствующие им изотермы адсорбции:

А ■— конусообразная нора: 6—цилиндрическая мора с одним открытым концом; в цилиндрическая пора с двумя открытыми концами

Капиллярно-конденсационный гистерезис часто обусловлен и кинетическими причинами. Например, он может быть связан с проявлением гистерезиса смачивания. Сухая поверхность с адсорбированным воздухом хуже смачивается водой (потенциальный барьер), поэтому для заполнения пор требуется давление водяного пара несколько больше равновесного. При десорбции испарение пронсходіп из пор, полностью смоченных водой. Б отсутствие адсорбирп ванного воздуха угол смачивания меньше и сответственно ниже давление пара при той же степени заполнения пор (пли величине адсорбции).

Капиллярная конденсация описывается уравнением Кельви на, в которое входит радиус кривизны мениска, и это позволя ет использовать его для расчета функции распределения пор по размерам. В принципе количественная характеристика дисперсных систем по дисперсности может быть представлена рас пределепием массы, объема, числа >іастиц и других параметров по радиусу, поверхности, объему, массе и др. Перейти от одного вида распределения к другому сравнительно просто, особенно если поры или частицы имеют правильную форму. Метол расчета функций распределения частиц (пор) по размерам за ключается в построении интегральных и дифференциальных кривых распределения.

Для пористых тел принято характеризовать распределение пор по их радиусам, поэтому интегральная кривая распределения выражает зависимость общего объема пор от их радиуса:

Дифференциал от общего объема пор, или объем пор, имеющих радиус в пределах от г„ до R„—DrH, равен

Интегрированием этой функции в пределах or г„ = 0 до г„

оо находят общий объем пор У0 в данной пробе или в единице массы пористого тела; при построении кривых распределения часто этот объем пор принимают за единицу или за 100%:

Если же интегрирование проводят в пределах от гп1 до г„2, то получают объем пор данной функции, или долю от общего объема, приходящуюся на эту фракцию: R—Z га

Очевидно, что чем меньше различаются пределы интегрирования, тем ближе к истинным значениям функции распределения. Как следует из соотношений (III.76) — (III.78), другой функцией распределения для данного пористого тела является зависимость /'(гп) или DV„/Dr„ от гп, которая называется дифференциальной кривой распределения. Она более четко и наглядно характеризует полидисперсность системы.

Для получения кривых распределения по методу капиллярной конденсации используют десорбционную ветвь изотермы адсорбции (см. рис. III.11), так как для всех без исключения пор она соответствует сферическим менискам, радиусы которых принимают за радиусы пор. Каждой точке кривой соответствуют определенные величины адсорбции А и относительного давления пара P/Ps. Зная величину адсорбции А, можно вычислить объем заполненных пор при данном давлении по уравнению, аналогичному (III.67):

Эффективный радиус сферического мениска г, соответствующий данному относительному давлению Pips, находят по уравнению Кельвина (III.72). Так как поры заполняются в Результате капиллярной конденсации после полимолекулярной адсорбции на стенках пор, то истинное значение радиуса пор гп равно сумме радиуса мениска г при полном см-ачивании и толщины адсорбционного слоя t2дс:

Гп = Г-Иадс (III.801

Величину ^адс определяют при том же давлении в отдельном эксперименте по адсорбции на непористых или макропористых адсорбентах той же природы (необходимо отсутствие капиллярной конденсации) и рассчитывают по формуле

Где Лнп — величина адсорбции на непористом адсорбенте при соответствующем давлении; 5уд— удельная поверхность непорнстого адсорбента.

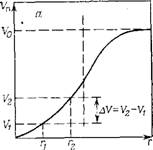
Зная Vn (III.79) и соответствующие значения Rn (III.80), строят интегральную кривую распределения (III.75), типичный вид которой представлен на рис. 111.13а. Чтобы избежать случайных погрешностей, интегральную кривую «выравнивают» (т. е. усредняют) и после этого с помощью графического диф-

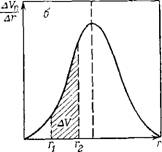
Рис. III. ІЗ. І Інтегральная (а) и дифференциальная (б) кривые распределения объема нор по их радиусам

Ференцирования строят дифференциальную кривую распределения (рис. III.136). Каждая точка на интегральной кривой распределе ния, например, V< при Гі дает объем пор с радиусами от минимального до Г]. По этой кривой можно определить объем пор Al/=l/2—Vi с радиусами от г, до г2 и общий объем пор V0 (рис. 111.13а).

По дифференциальной кривой распределения объем пор (или долю от общего объема пор), размеры которых лежат в пределах от г, до г2 (т. е. объем данной фракции пор) определяется площадью, заключенной между осью абсцисс, дифференциальной кривой и ординатами л и г2 (рис. 111.136). Чем резче выражен максимум н уже дифференциальная кривая, тем меньше различаются поры по размерам.

Из кривых распределения видно, что общий объем малых пор относительно небольшой. Однако доля поверхности, приводящаяся на эти поры, существенно большая. С увеличением размера пор объем растет быстрее, чем поверхность, и в связи с этим максимум дифференциальной кривой распределения поверхности по размерам пор сдвинут в сторону меньших радиусов. Построение разных кривых распределения позволяет более правильно представить структуру пористого тела, например, судить о степени полидисперсности.

Существует метод исследования и построения кривых распределения, не требующий предположений относительно формы пор. Этот «безмодельный» метод основан на общем термодинамическом соотношении, полученном А. В. Киселевым:

Где Ар. — изменение химического потенциала адсорбата (адсорбционный потенциал с обратным знаком), dn — число молей жидкости, сконденсированное в порах; ds — уменьшение поверхности адсорбента в результате заполнения пор адсорбатом.

Соотношение (111.82) показывает эквивалентность превращения поверхностной энергии в химическую (энергию адсорбции) .

Чтобы найти удельную поверхность адсорбента, необходимо проинтегрировать уравнение (III.82) во всей области капиллярной конденсации: от максимальной поверхности (начало капиллярной конденсации) до минимальной (максимальное заполнение пор). Так как при максимальной степени заполнения пор свободной поверхностью можно пренебречь, то поверхность s адсорбента равна:

Где пк — число молей адсорбированной жидкости, отвечающее началу гисто — резисной петли.

Для построения кривых распределения пор по размерам всю область капиллярной конденсации от пк до пх разбивают на отдельные участки, которым соответствуют определенные приращения поверхности. Зная изменения An и соответствующие им As, можно рассчитать размеры пор и построить кривые распределения. Необходимо обратить внимание на то, что данный метод не учитывает изменения поверхности, которое происходит до гистерезисной петли. Однако эти изменения слабо влияют на удельную поверхность и размер пор.

Видео:Линейные диофантовы уравненияСкачать

Адсорбция и адсобционные равновесия

Адсорбция на границе раздела «твердое тело-газ». Классификация пористых тел по Дубинину. Капиллярная конденсация. Уравнение Томсона (Кельвина). Капиллярно-конденсационный гистерезис. Теория объемного заполнения пор. Теория Поляни

Адсорбция — процесс самопроизвольного перераспределения компонентов системы между поверхностным слоем и объемом фазы.

Адсорбция может наблюдаться в многокомпонентных системах и при перераспределении в поверхностный слой уходит тот компонент, который сильнее понижает поверхностное натяжение. В однокомпонентной системе при формировании поверхностного слоя происходит изменение его структуры — уплотнение, которое называется автоадсорбцией.

В общем случае адсорбция может происходить не только благодаря стремлению поверхностной энергии к уменьшению, но и за счет химической реакции компонентов с поверхностью вещества. В этом случае поверхностная энергия может даже увеличиваться на фоне снижения энергии всей системы.

Вещество, на поверхности которого происходит адсорбция, называется адсорбентом, а вещество, которое перераспределяется — адсорбатом.

Обратный процесс перехода вещества с поверхности в объем фазы — десорбция.

В зависимости от агрегатного состояния фаз различают адсорбцию газа на твердых адсорбентах, твердое тело — жидкость, жидкость — жидкость, жидкость — газ. Для количественного описания адсорбции применяют две величины: первая измеряется числом молей или граммами, приходящимися на единицу поверхности или массы адсорбента:

Величина, определяемая избытком вещества в поверхностном слое, также отнесенным к единице площади поверхности или массы адсорбента, называется Гиббсовской или относительной адсорбцией (Г).

Рис. 1. Серия изотерм, полученных при различных температурах

Адсорбция зависит от концентрации компонентов и температуры.

Различают следующие виды зависимостей:

1. Изотерма (рис. 8)

Поскольку в качестве твердых адсорбентов используют пористые тела, рассмотрим некоторые методы получения твердых тел. Основных методов два.

Первый метод заключается в синтезе гидрозоля, который затем подвергают коагуляции до получения геля. Гель высушивают, частицы в результате этих операций срастаются с образованием твердого каркаса. Так как частицы золя высокодисперсны, то пористый материал получается с большой удельной поверхностью. Для удобства использования комки дробят, таблетируют, гранулируют. Обычно размер зерен адсорбента имеет предел от 0.1 до 7 микрон. Таким образом получают силикагель и другие адсорбенты.

Второй метод заключается в обработке крупнопористых материалов агрессивными газами или жидкостями. При такой обработке образуется губчатая структура. Этим методом получают активированный уголь из природных материалов, из которых сначала удаляют летучие вещества при нагревании без доступа воздуха. В результате образуется крупнопористая структура. Затем активируют уголь путем окисления газом кислорода или СО₂, или водяным паром. Таким же образом получают никель Рэнея, т.е. берут сплав никеля и алюминия и его высушивают.

По классификации М.М. Дубинина за основу принят размер пор и механизм протекающих на них процессов.

Макропористые тела. Радиус пор от 100 — 200 нм, S_уд= 0.5 — 2 м 2 /г — Для этих же адсорбентов пригодна теория адсорбции Ленгмюра. В адсорбентах и катализаторах макропоры выступают в качестве транспортных каналов и адсорбцией в них можно пренебречь.

Переходно-пористые тела. Радиус пор более 2 — 100 нм, S_уд= 100 — 500 м 2 /г. Для них характерна полимолекулярная адсорбция, которая с увеличением давления заканчивается капиллярной конденсацией.

3. Микропористые тела. Радиус пор 0.5 — 2 нм, Sуд = 500 — 1000 м2/г. Отличительной особенностью этих тел является чрезвычайно близкое расположение противоположных стенок в порах. При этом их поля поверхностных сил перекрываются и они действуют во всем объеме микропор. К ним применима теория объемного заполнения микропор.

Реальные и промышленные адсорбенты имеют набор всех пор, но соотношение пор с разными радиусами различно. Каких пор больше, к такому классу их и относят.

Как уже отмечалось, влияние структуры пористого тела на адсорбцию заметно проявляется уже на переходно-пористых телах. Это обусловлено проявлением капиллярных сил. Появление этого связано со сродством адсорбата к адсорбенту. Основываясь на закономерностях капиллярных явлений, можно утверждать, что сродство должно быть достаточно для смачивания поверхности твердого тела жидкостью, появляющейся в результате конденсации в порах. Только в случае смачивания адсорбент будет втягивать в поры адсорбат, увеличивая тем самым адсорбцию. Чем меньше размер пор, тем сильнее капиллярное удерживание адсорбата. Если поверхность не смачивается, то наблюдается явление капиллярного выталкивания, адсорбция в этом случае минимальна и возможна только в крупных порах. Адсорбция в переходно-пористых телах происходит по механизму капиллярной конденсации. Капиллярная конденсация начинает проявляться при определенной степени заполнения адсорбента или при определенном давлении пара, характерном для данной системы. К этому моменту поверхностная энергия адсорбции практически полностью скомпенсирована в результате полимолекулярной адсорбции, а макропоры заполнены адсорбатом. В результате повышения давления пара заполняются конденсатом все крупные поры. Размеры радиусов менисков подчиняются уравнению капиллярной конденсации Томсона (Кельвина).

где р — давление пара над искривленным мениском;

р_s— давление насыщенного пара над плоской поверхностью;

— поверхностное натяжение конденсированной жидкости;

r — радиус кривизны мениска.

Рис. 2. Изотерма адсорбции при капиллярной конденсации: 1 — адсорбционная кривая; 2 — десорбционная кривая

Из уравнения видно, что при смачивании обеспечивается отрицательная кривизна мениска конденсата (вогнутый мениск), конденсация в порах наступает при давлении, которое меньше давления насыщенного пара, т.е. р/р_s n ]

— общие уравнения теории объемного заполнения микропор.

В логарифмическом виде они имеют линейную форму:

адсорбция равновесие мономолекулярный

Адсорбционное равновесие в системе «газ — жидкость». Закон Генри. Мономолекулярная адсорбция в системах «газ — жидкость», «жидкость — жидкость», «газ — твердое». Изотерма адсорбции Ленгмюра. Уравнение Фрейндлиха. Теория полимолекулярной адсорбции БЭТ. Уравнение БЭТ

Предположим, что имеются компоненты-неэлектролиты. Будем считать, что адсорбат образует на поверхности адсорбента мономолекулярный слой. Мономолекулярная адсорбция с точки зрения термодинамики процесса выражается химическим потенциалом в адсорбционном слое и объемной фазе:

где — химический потенциал вещества в адсорбционном слое;

— химический потенциал вещества в объемной фазе.

При равновесии потенциалы равны: .

, где D — коэффициент распределения.

Выражение — константа Генри. Она не зависит от концентрации, определяется при постоянной температуре, A/a=Kг,

А=аК_г — закон Генри, т.е. при разбавлении системы коэффициент распределения стремится к постоянному значению, равному константе Генри. Если концентрация в сорбционном слое стремится к нулю, то а с; а = ?с; ? 1. Поэтому на практике закон Генри используют в следующем виде: а=К_гс_i. Если одна из фаз — газ, то имеем следующий вид: a = К_гР_i,

Рис. 7. Изотерма адсорбции Генри (отрицательные и положительные отклонения от закона Генри)

Эти уравнения представляют собой уравнения изотермы адсорбции при малых концентрациях. В соответствии с этими уравнениями можно по другому сформулировать закон Генри: величина адсорбции при малых давлениях газа (малых концентрациях вещества в растворе) прямо пропорциональна давлению (концентрации). Эти зависимости показаны на рисунке 7. При адсорбции на твердых телах область действия закона мала из-за неоднородности поверхности, но даже на однородной поверхности при увеличении концентрации обнаруживается отклонение от закона. При малых концентрациях распределенного вещества отклонения обусловлены в основном соотношением между взаимодействием молекул друг с другом и с поверхностью адсорбента. Если когезионные взаимодействия адсорбата больше, то отклонение от закона отрицательно и ? в уравнении характеризуют энергию взаимодействия адсорбента с адсорбатом. Адсорбционное уравнение часто представляют относительно степени заполнения поверхности, т.е. как отношение А/А:

Экспериментальные результаты по определению изотермы адсорбции обычно обрабатывают с помощью уравнения, записанного в линейной форме;

, т.е. уравнение типа y = b + ax.

Такая линейная зависимость позволяет графически определить А и К. Зная А, можно определить удельную поверхность адсорбента (поверхность единицы массы адсорбента):

где А — предельная адсорбция, выражаемая числом молей адсорбата на единицу массы адсорбента;

0 — площадь, занимаемая одной молекулой адсорбата.
1. Если с 0, тогда уравнение примет вид:

т.е. при с 0 уравнение Ленгмюра переходит в уравнение Генри.

2. Если с, тогда А = А, А/А = 1. Это случай предельной адсорбции.
3. Пусть адсорбция идет из смеси компонентов, в этом случае уравнение Ленгмюра записывается следующим образом:

Все рассмотренные выше уравнения справедливы для мономолекулярной адсорбции на адсорбенте с энергетически эквивалентными адсорбционными центрами. Однако реальные поверхности этим свойством не обладают. Приближенной к реальности является возможность распределения адсорбционных центров по энергии. Приняв линейное распределение, Темкин использовал формулу уравнения Ленгмюра и получил уравнение для средних степеней заполнения адсорбента.

где ? — константа, характеризующая линейное распределение;

К₀ — константа уравнения Ленгмюра, отвечающая максимальной теплоте адсорбции.

Из уравнения следует, что увеличение парциального давления (из-за увеличения концентрации) одного компонента подавляет адсорбцию другого и тем сильнее, чем больше его адсорбционная константа равновесия. Уравнение часто называют логарифмической изотермой адсорбции. Если принять экспоненциальное распределение центров по поверхности, то в области средних заполнений получается ранее найденное эмпирическим путем уравнение Фрейндлиха:

где K, n — постоянные.

Использование уравнения Фрейндлиха в логарифмической форме позволяет определить константу уравнения.

Уравнение Ленгмюра можно использовать только при адсорбции в мономолекулярном слое. Это условие выполняется при хемосорбции, физической адсорбции газов при меньшем давлении и температуре выше критической.

Рис. 8. Изотерма полимолекулярной адсорбции

Рис. 9. Схема полимолекулярной адсорбции по теории БЭТ

Однако в большинстве случаев мономолекулярный адсорбционный слой не компенсирует полностью избыточную поверхностную энергию и поэтому остается возможность влияния поверхностных сил на второй и т.д. адсорбционные слои. Это реализуется в том случае, когда газы и пары адсорбируются при температуре ниже критической, т.е. образуются полимолекулярные слои на поверхности адсорбента, что можно представить как вынужденную конденсацию (рис. 8 и 9).

В результате этих представлений была выведена следующая формула:

— уравнение полимолекулярной адсорбции БЭТ,

а_ж— активность вещества в жидкости;

а_п— активность вещества в состоянии насыщенного пара;

Физический смысл С: характеризует разность энергии Гиббса в процессах чистой адсорбции и конденсации. Это уравнение получило название БЭТ (Бранауэр-Эммет-Теллер).

Видео:9 класс, 26 урок, Комбинаторные задачиСкачать

Размер пор и распределение пор по размерам

Такие характеристики могут оцениваться несколькими способами из изотерм десорбции. Брокхофф и Линеен [149] представили по этому вопросу достаточно подробный обзор. В дополнение к трудоемкому приему точного измерения изотерм адсорбции в большинстве методов предусматривается проведение отдельно расчетов для большого числа интервалов рассматриваемой изотермы. Однако при значительно усовершенствованном способе измерения и выдачи получаемых результатов, возможности для обработки получаемых данных и составления программ для обсчета размеров пор на ЭВМ подобная работа значительно упрощается,

В настоящее время доступны два типа коммерческих приборов для проведения подобного рода измерений. В одном используется вакуумная система, как и в оригинальном методе

БЭТ (прибор Micromeritics), а в другом — система потока газа (прибор Quantachrome). Изотерма с 10—15 равновесными точками может быть измерена в течение нескольких часов, и значения удельной поверхности и распределение пор по размерам могут быть получены довольно быстро [150, 151].

За прошедший век были разработаны различные математические приближения для расчета распределения пор по размерам.

В большинстве методов предусматривается построение t* кривой, поскольку необходимо учитывать то, что на относительно гладкой поверхности в отсутствие пор происходит адсорбция и адсорбционная пленка оказывается толщиной в несколько молекулярных слоев, прежде чехМ давление пара достигает значения р/ро=1Д соответствующего образованию жидкости. Очевидно, в такой толстой пленке, состоящей из нескольких слоев, свойства азота не будут теми же самыми, что и для нормальной жидкости. Как уже отмечалось, определение пор по размерам требует не только использования уравнения Кельвина для подсчета размеров пор, которые заполняются жидким азотом, имеющим свойства нормальной жидкости, но также и знания толщины адсорбционной пленки на внутренней поверхности пор, еще не заполненных азотом.

Чтобы получить экспериментальные данные, учитывающие толщину пленки, исследуемый кремнезем не должен содержать микропор. Харрис и Синг [152] изучили ряд таких образцов кремнезема (с удельной поверхностью менее 12 м2/г) и показали возможность проведения усредненной по рассмотренным ими образцам изотермы в виде зависимости величины vjvm от pipe. Однако с тех пор были проведены многочисленные исследования на соответствующих непористых кремнеземах с целью точного определения t-значений. Бебрис, Киселев и Никитин [153] ‘приготовили очень однородный широкопористый кремнезем, не содержащий микропор, посредством термообработки пирогенного кремнезема (аэросила) в парах воды при 750°С, получив указанный кремнезем с удельной поверхностью около 70—80 м2/г и порами диаметром около 400 А. Обычно принимаемые значения толщины пленки t для различных значений р! ро при использовании азота основаны на данных Липпенса, Линсена и де Бура [154] и де Бура, Линсена и Осинда [155].

В табл. 5.4 представлены типичные ^-значения в зависимости от р/р0. Приводимое ниже уравнение дает возможность подсчитывать толщину пленки с учетом большей части опубликованных данных по усредненным значениям t при относительном давлении р/ро выше 0,3:

Парциальное давление азота и толщина пленки азота, адсорбированного на непористой поверхности при температуре — 195°С (по данным [154])

Как описано Брокхоффом и Линсеном [156], многие исследователи сделали вклад в развитие методов расчета распределения пор по размерам из изотерм адсорбции. Первоначальный подход и общее уравнение, разработанные Барретом, Джойне — ром и Халендой [157], были доведены до конца Пирсом [158] и позднее Кранстоном и Инкли. Последующее развитие этой проблемы было подробно описано Грегом и Сингом [7].

Метод Крэнстона и Инкли. Крэнстон и Инкли (39), используя известную толщину пленки t адсорбированного азота на внутренних стенках пор наряду с заполнением пор азотом по механизму, описываемому уравнением Кельвина, разработали метод расчета объема и размеров пор из десорбционной или адсорбционной ветвей изотермы. Расчет ведется на участке изотермы выше р/ро>0,3, где уже имеется адсорбированный по крайней мере мономолекулярный слой азота.

Метод представляет собой ступенчатую процедуру подсчета, которая, хотя и проста, но предусматривает такие подсчеты на каждом очередном этапе. Изотерма десорбции состоит из серии экспериментальных точек, в каждой из которых имеются данные по измеренному объему адсорбированного газа при определенном давлении. Начиная от точки р/ро =1,0 при полностью заполненных порах, ступенчато понижают давление и при этом на каждом этапе замеряют адсорбированный объем (это относится к изотерме десорбции, но процедура расчетов будет той же самой и при рассмотрении изотермы адсорбции). По мере того как давление понижается от значения рі/р0 до Рг/Роі справедливыми оказываются следующие положения:

1. Объем жидкого азота AVuq испаряется из пор, образуя при этом газ объемом AVg, который обычно выражается в кубических сантиметрах при нормальных условиях в расчете на 1 г адсорбента.

2. Объем AVnq жидкого азота, который был удален из пор в интервале размеров их радиусов между г і и г2, оставляет на стенках этих пор пленку азота толщиной t2.

3. В порах, опорожненных на предыдущих этапах, толщина пленки азота на стенках понижается от t до t2.

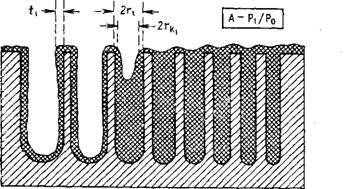
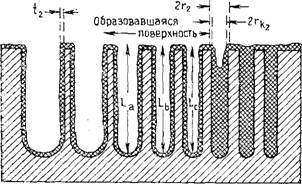
Читателю, незнакомому с этим вопросом, может помочь схематическое изображение процесса, представленное на рис. 5.11. На рисунке показано поперечное сечение образца с идеализированными порами цилиндрической формы, которые различаются по своим диаметрам. Видно, что когда давление в системе понижается от рі (положение А) до р2 (положение В), толщина пленки азота на стенках опорожненных капилляров уменьшается от tx до t2, количество жидкого азота уменьшается в результате десорбции и при этом увеличивается число пустых пор.

В положении А (рис. 5.11) имеется одна частично заполненная пора диаметром 2гь в которой жидкий азот находится в данный момент в равновесии с паром при давлении рх. Аналогично имеем в положении В одну пору диаметром 2г2, в которой содержится жидкий азот, находящийся в равновесии при давлении р2. В указанных порах радиус определяется как fp = t + rk, где гь — радиус, подсчитываемый из уравнения Кельвина при данном давлении. Расчеты основаны на использовании следующих уравнений. Пусть L — длина, равная суммарной длине всех опорожненных пор с радиусами в интервале от г, до г2, а гр — среднее значение радиуса. Тогда суммарный объем испаренного жидкого азота Vuq на данном этапе равен

Vuq = 3,14 (rp — t2f L + (t2- tx) Z Л

Где А — поверхность адсорбционной пленки, оставшейся в указанных опорожненных порах.

Средний объем пор радиусом гр составляет

А V р = nfpL Исключив величину L, получим

Так как rv — t = ru, где Гк находится из уравнения Кельвина, то

Объем выделившегося газа, измеряемого при давлении р и температуре ТК, соответствует объему жидкости

Рис. 5.11. Схема воображаемого адсорбента с набором цилиндрических пор, показанных в разрезе, когда азот адсорбируется при двух давлениях и рг — Л—давление pi. Все поры, имеющие радиус менее п, заполнены жидким адсорбированным веществом. Адсорбционная пленка имеет толщину tu а раднус Кельвина в поре,

Заполненной под воздействием поверхностного натяжения, равен г, .

В— давление Рг (P2

Рожненных по мере того, как давление понизилось от рt до рэ (см. текст).

Площадь А внутренней поверхности рассматриваемых пор при допущении, что они являются цилиндрическими, оказывается равной

Где Vp выражается в сантиметрах кубических, а радиус гр — в ангстремах.

Используя данные по десорбции, расчеты начинают при р/р0 вблизи 1,0, когда поры фактически заполнены жидким азотом. Крэнстон и Инкли описали поэтапные подсчеты объема пор и поверхностей опорожненных пор. Тем не менее детализация такого рассмотрения будет полезна.

Расчеты выполняются на каждом этапе при фиксированном давлении, начиная с заполненных пор и относительного давления р/ро, близкого к 1,0. Для каждого этапа подсчиты — ваются следующие значения:

1. Среднее значение? ь. из двух кельвиновских радиусов Гк, и Гьг при соответствующих давлениях рі и р2, выражаемое в ангстремах. Каждое значение подсчитывается из уравнения Кельвина

2. Толщины пленок 11 и t2 при давлениях рх и р2, выражаемых в ангстремах. Каждая толщина t берется из таблиц или определяется из уравнения

3. Средний радиус пор гр в данном интервале:

Гр = 0,5 [г + г к, + t2)

4. Значение t=t — t2, выраженное в ангстремах.

5. Объем десорбированного жидкого азота AVnq в расчете на единицу массы адсорбента, AVuq = 1,55-Ю-3 AVg, см3/г, где AVg — объем выделившегося газообразного азота, приведенный к нормальным условиям, см3.

6. Объем жидкого азота, теряемый на данном этапе за счет утоньшения пленок на стенках пор и равный (A0″(Z^)> где 2 А — поверхность стенок всех пор, опорожненных в процессе десорбции на всех предыдущих этапах (или АЛ для первого этапа). Указанный объем равен (At) • (£ А) • 10

4 и имеет размерность см3, поскольку At выражено в ангстремах, а

В квадратных метрах.

7. AA — 2(AVnq) • Рр• 104.

8. Значение £ А находится посредством суммирования всех значений ДА из предыдущих этапов.

Указанный процесс расчета является необходимым на каждом этапе такого ступенчатого метода. Серия расчетов выполняется для каждого этапа поочередно по мере понижения давлений, и полученные результаты сводятся в таблицы.

Совокупный объем пор Vc, начиная от р/ро = 0,3 и вплоть до наибольшего значения р/ро, представляет собой просто сумму значений AViiq, получаемых на каждом этапе. Как правило, вычерчивается графическая зависимость Vc от lg гр.

Совокупная поверхность Лс— это общая сумма значений АЛ, получаемых на каждом этапе. Если микропоры отсутствуют, то Ас обычно составляет значения, достигающие 85—100 % величины поверхности, определяемой методом БЭТ. Так как последняя получается при измерениях в области более низких значений р/р о от 0 до 0,3, то такое согласие указывает на отсутствие микропор в образце.

Крэнстон и Инкли пришли к заключению, что для многих силикагелей рассмотренный метод целесообразно использовать и в обратном направлении, начиная от значения р/р0 = 0,3 и проводя измерения и расчеты на последующих этапах по мере получения изотермы адсорбции.

Хоуген [159] представил дальнейшее обсуждение метода Крэнстона и Инкли и дал некоторые полезные номограммы. Однако оказалось не так просто перевести систему уравнений в способ практических расчетов, именно поэтому обсчет рассмотренных выше этапов был показан столь детально.

Распределение пор по размерам может оцениваться из ^-диаграммы в соответствии с данными Брокхоффа и де Бура [160].

Микропоры. Особого рода проблемы возникают при измерении и описании пор чрезвычайно малых размеров. В данной книге невозможно дать обзор всего имеющегося огромного литературного материала, появившегося за последнее десятилетие, но будет предпринята попытка дать описание некоторых аспектов по этой проблеме, сопроводив их примерами.

Согласно Брунауэру, в основном принято считать, что «механизм адсорбции молекул в микропорах не достаточно хорошо понят» [35]. Синг [161] в 1976 г. констатировал, что «не разработано ни одного заслуживающего доверия метода для определения распределения микропор по размерам». Однако совершенно ясно, что адсорбция в микропорах отличается коренным образом от адсорбции на поверхности стенок широких пор и на открытых поверхностях и что молекулы в таких тонких порах подвергаются действию притяжения со стороны окружающего твердого тела и находятся в состоянии сильного сжатия. Дубинин [124] обсудил теорию адсорбции в подобных условиях, которая включает понятие «объема микропор», более точно описывающее процесс, чем понятие поверхности таких пор.

Согласно Оккерсу [162], удельная поверхность в микропористых материалах не может быть определена, если радиус микропоры оказывается менее 12 А. Этот автор использовал термин «субмикропора», подразумевая под этим понятием
то же самое, что и другие исследователи, в том числе Айлер, который применял термин «микропора». Оккерс обобщил возможное применение ряда уравнений, которые были предложены для пор наименьших размеров.

О 2 4 6 8 10 12 14

Толщина пленки t, A

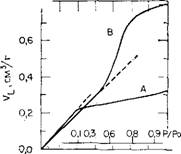
Рис. 5.12. Типичные t-диаграммы

Для двух кремнеземных порошков, имеющих примерно одинаковое значение удельной поверхности.

А — микропористый образец; В — макропористый образец. VL — объем адсорбированного жидкого азота, см;!/г; / — толщина адсорбционной пленки азота.

Рис. 5.13. Типичные Gts-диаграммы.

А — широкопористый силикагель оез наложения ограничений на мономолекулярную н полимолекулярную адсорбцию, но в отсутствие адсорбции в капиллярах; В — конденсация в мезопо — рах„ вследствие чего данная кривая отклоняется от прямой Л; С — адсорбция в микропорах; заполненный объем микропор составляет Vp, as=x/xl, где xs — количество адсорбированного вещества при р/ро—0,40 их — количество адсорбированного вещества при других относительных давлениях.

Как четко было продемонстрировано Брокхоффом и Линсе — ном [163], микропоры могут быть обнаружены путем изучения изотерм адсорбции, изображенных в виде /-кривых. Если на графике линия, изображающая зависимость Va от /, отклоняется вниз в сторону /-оси, то это является указанием на присутствие в образце микропор. Аналогичные графики, полученные Михаилом [164], представлены на рис. 5.12 для двух силикагелей. Поскольку значения удельных поверхностей образцов близки, то линии на /-диаграммах имеют примерно одинаковый наклон. Для силикагеля А, который является микропористым и плотным, /-кривая начинает отклоняться вниз в сторону /-оси при относительном давлении р/ро= 0,1. Для мезопористого силикагеля В, имеющего низкую плотность, /-кривая отклоняется вверх примерно при р/ро = 0,5, т. е. когда начинают заполняться широкие поры. В подобных гелях, имеющих однородные по размеру поры, легко показать наличие микропор. Однако для мно
гих силикагелей большая доля поверхности принадлежит мезо — порам и только небольшая часть — микропорам. В таком случае отклонение от линейности на /-кривой трудно определять. Миевилл [165а] исследовал твердые материалы смешанной структуры, обладавшие мезопорами и микропорами. Он применил метод /-диаграммы и показал, что в таком образце со смешанной структурой 10 % составляют микропоры.

Используя as-диаграмму, Синг [8] показал наличие мезо — пор по отклонению от линейности по отношению к ав-оси при более высоких значениях as. Наличие микропор доказывается отклонением кривой в сторону as-оси при более низких значениях cc. s. Экстраполяция линейного участка к оси х позволяет определить объем микропор (рис. 5.13). Авторы работы [50] провели дальнейшие исследования в этом направлении с большим набором кремнеземов и дали объяснение отклонениям на основе представлений о микропорах и мезопорах.

Рамзай и Эвери [1656] получили данные по адсорбции азота в плотных спрессованных микропористых кремнеземах. Они строили по своим данным графики, используя уравнение[10]

Пирогенный кремнеземный порошок с размером частиц 3—4 нм прессовался до получения значений объемов пор 0,22—0,11 см3/г (плотности упаковки кремнезема составляли 67—80 %), что соответствовало образованию пор диаметром 22—12 А. На графиках, представленных в координатах указанного уравнения, видно уменьшение наклонов линий для серии образцов, что свидетельствует о происходящих в них изменениях в области от полного заполнения объема пор до монослойного покрытия (когда монослой адсорбата заполняет и наиболее тонкие поры). В этой работе константа С на графике, построенном в координатах БЭТ, имела значение 73 для исходного, непрессованного порошка и увеличивалась от 184 до более чем 1000 по мере. того, как диаметр пор уменьшался от 22 до 12 А.

Метод «модельных пор» (МП). Брунауэр, Михаил и Бо — дор [166] разработали метод для определения характеристического распределения пор по размерам, включая даже часть области, занимаемой микропорами.

По методу Крэнстона—Инкли, включающему также /-кривую и уравнение Кельвина, кривые, характеризующие пористую структуру образца, могут рассчитываться для пор радиусами от 10 до 150 А. Однако полученные результаты’ зависят от принятого допущения о цилиндрической форме пор. Так как на самом деле поры не являются цилиндрическими, то расчет распределения пор по размерам не отражает реального положения дел, особенно при наличии небольших по размеру пор.

В методе «модельных пор» вводится понятие гидравлический радиус» rh, определяемый как rh = V/S, где V — объем пористой системы и 5 ■—• поверхность стенок пор. Соотношение применимо к порам любой формы. Значения V и S подсчиты- ваются из изотерм адсорбции или десорбции. Когда происходит десорбция и какая-то группа пор оказывается опорожненной,, то монослой молекул азота остается на их стенках при давлении р. Опорожненное пространство поры называется «сердцевиной». Эта величина представляет собой десорбированный объем ■ по мере того, как давление понизилось от р0 до р.

Данный метод отличается от метода Крэнстона и Инкли еще и тем, что в нем вместо уравнения Кельвина используется уравнение Киселева

Где у — поверхностное натяжение; ds — поверхность, которая исчезает по мере заполнения поры; — изменение химического потенциала, da — число молекул жидкости, находящихся в поре. (Уравнение Кельвина представляет собой частный случай приведенного выше уравнения Киселева, если рассматриваются поры цилиндрической формы.) Изменение химического потенциала рассчитывается по уравнению —Лр = = —RT In (р/р0). Интегрирование дает

Где ah — число адсорбированных молекул в начале гистере — зисной петли — и as — число адсорбированных молекул при насыщении.

Последнее уравнение интегрируется графически по этапам:

1. При десорбции ai молей вещества относительное давление р/ро понижается от 1,0 до 0,95.

2. Образующийся объем всех сердцевин будет равен произведению а на мольный объем адсорбата; для случая азота он составляет 34,6 а см3.

3. Si—площадь поверхности образующихся сердцевин определяется по уравнению

Интегрирование проводится графически.

4. rh — гидравлический радиус, равный образующемуся объему сердцевин (этап 2), деленному на площадь поверхности таких сердцевин (этап 3).

Затем на n-м этапе, когда десорбируется ап молей, наблюдается следующее:

1. Понижение относительного давления р/ро от рп/ро до pn-l/po-

2. Образующийся объем сердцевин равен 34,6 ап см3. Однако когда вещество десорбируется, то добавляется некоторый объем

Адсорбата v„ со стенок пор, образовавшихся на предыдущих

Этапах. Этот объем vn подсчитывается на основании построения /-кривой, что позволяет определить значение At, т. е. уменьшение толщины жидкой пленки по всей суммарной поверхности сердцевин, образовашихся до этого момента. Объем, таким образом, равен произведению At на суммарную поверхность сердцевин. Введение такой поправки является ключевым моментом расчета.

3. Разность а„ — vn дает значение объема вновь образуемых сердцевин на n-м этапе.

4. Площадь поверхности новых сердцевин Sn определяется графическим интегрированием, как и „на предыдущих этапах.

Указанного объяснения достаточно, чтобы показать различие между таким «скорректированным методом модельных пор» и методом Крэнстона—-Инкли. Для более подробного ознакомления с описанием метода и примерами расчетов необходимо обратиться к первоисточнику [166].

В большинстве случаев метод» «модельных пор» дает меньшее значение радиуса пор в максимуме кривой распределения, чем то, которое получается по методу Крэнстона и Инкли. Например, для образцов с радиусами пор в интервале 5—10 А при использовании изотермы десорбции по данному методу получено значение радиуса в максимуме кривой распределения около 6 А, а по методу Крэнстона—Инкли 10 А. Ханна и др.

[167] для широкого набора различных силикагелей получили хорошее согласие в значениях размеров пор, используя азот или кислород в качестве адсорбата при двух различных температурах эксперимента. В некоторых случаях, отмеченных в данной работе, образцы кремнезема содержали как микро-, так и мезопоры.

Стандарт для определения размеров пор. Гавард и Уилсон

[168] описали применение метода «модельных пор» на образце мезопористого кремнезема Gasil(I), состоящего из сфер со средним радиусом 4,38 нм, упакованных с координационным числом 4. Такой кремнезем является одним из стандартов

SCI/IUPAC/NPL для определения удельной поверхности и может также использоваться в качестве стандарта для определений размеров пор и для калибрования аппаратуры, работающей на принципе метода БЭТ во всей области давлений.

МП-метод был продемонстрирован Михаилом, Брунауэром и Бодо [164]. Они показали применимость этого метода к изучению микропор, а «скорректированного метода модельных пор» — к исследованию пор большого размера. При применении этого метода к силикагелю, имеющему как микро-, так и мезопоры, МП-метод дает совокупное значение поверхности пор, согласующееся со значением, найденным методам БЭТ. Этот факт указывает, что, несмотря на возражения, выдвигаемые против применения метода БЭТ для изучения микропористых образцов, данный метод, как можно надеяться, способен давать надежные данные по удельным поверхностям даже и в этих случаях.

Подробное рассмотрение структуры пор для пяти силикагелей, выполненное Хагемасси и Брунауэром [169], может считаться типичным для работ подобного рода, в которых оценивалась структура пор с применением МП-метода. В этой статье проводилось сравнение паров воды и азота в качестве адсорбатов, и полученные данные находились в достаточно хорошем согласии, давав значения диаметров пор в максимумах кривых распределения, равные 4,1 и 4,6 А соответственно. Однако для адсорбентов, имеющих какие-либо гидрофобные участки поверхности, должен использоваться азот.

Супермикропоры, Этот термин был предложен Дубининым [170] для пор с диаметрами 1,3—30,0 нм. Таким образом, классификация пор по размерам будет следующей:

Основанием для подобной предлагаемой классификации является то, что детальному исследованию могут быть подвергнуты супермикропоры и мезопоры, но не микропоры.

МП-метод подвергался критике [171], после чего последовало опровержение критических замечаний [47].

Ультрамикропоры или субмикропоры. Такие поры имеют радиус менее 3 А. Механизм, благодаря которому подобные поры заполняются, оставался главной темой обсуждений. Очевидно, что если наименьшая по размеру из известных молекула газа (гелия) не способна проникать в пору, то значит поры просто не существует, поскольку это подтверждается

Экспериментом. Таким образом, нижний предел размеров пор, при котором эти поры могут обнаруживаться, зависит от размера используемой молекулы адсорбата.

Основным вопросом является рассмотрение ситуации, когда молекула входит в пору, диаметр которой менее чем в два раза превышает размер молекулы. В этом случае вандервааль — сово взаимодействие очень сильно, и теплота адсорбции заметно выше, чем на плоской поверхности. Следовательно, подобная ситуация отличается от той, когда может происходить образование единичного полимолекулярного? лоя или капиллярное заполнение пор.

Согласно Доллиморе и Хилу [136], поры, диаметр которых, вероятно, равен 7—10 А, если они определяются на основании изотерм адсорбции азота, на самом деле имеют диаметр только лишь 4—5 А. Субмикропоры в силикагеле, приготовленном из частиц золя размером всего

10 А, оказываются настолько малыми, что даже в них не могут войти молекулы криптона. Известно, что монокремневая кислота быстро полимеризуется при низких значениях рН с образованием частиц примерно такого же размера. Доллиморе и Хил [172] приготовили такой гель по способу высушивания вымораживанием 1 %-ного раствора монокремневой кислоты при температуре ниже 0°С. Поскольку при испарении и вымораживании удалялось большое количество’ воды, то значение рН системы составляло в процессе гелеобразования 1—2, т. е. именно то значение, когда наблюдается наиболее медленный рост частиц. Такой кремнезем можно было бы назвать «пористым», так как в такие «поры» проникали молекулы гелия (и только лишь эти молекулы). Отметим, что молекулы гелия также проникают в плавленый кварц. Так что при общепринятом подходе такой кремнезем считается непористым.

Изостерическая теплота адсорбции. Значение теплоты адсорбции в микропорах оказывается аномально высоким. Синг и Рамакришна [173] обнаружили, что посредством тщательного выбора адсорбатов и применения а5-метода исследования можно различать капиллярную адсорбцию и адсорбцию на высокоэнергетических поверхностных центрах. Показано, что в интервале р/ро 0,01—0,2 изостерическая теплота адсорбции азота на силикагеле, не содержащем мезопоры, остается по существу постоянной на уровне 2,0 ккал/моль. На силикагеле, содержащем мезопоры, наблюдается падение теплоты от 2,3 до 2,0 ккал/моль, а на микропористом силикагеле изостерическая теплота падает от 2,7 до 2,0. Изостерическая теплота qst под — считывается из изотерм адсорбции по уравнению Клаузиуса— Клайперона.

Микропористость может просто характеризоваться построением графика зависимости изостерической теплоты от р/р0, получаемого по изотермам адсорбции азота.

Были проведены [174] калориметрические исследования микропористости, в которых измерили теплоту, выделяемую в процессе адсорбции бензола на силикагеле. Они подтвердили, что энергия адсорбции оказывается наивысшей в микропорах, и измерили поверхность, которая была еще доступна для адсорбции молекул азота при разных стадиях адсорбции бензола.

Дубищін [10] охарактеризовал микропористость, используя уравнение

Где а — количество адсорбированного вещества; Т — абсолютная температура; Wo — предельный объем микропор; v* — мольный объем адсорбата; В — параметр, являющийся характеристикой размеров микропор.

В том случае, когда в образце присутствуют поры двух размеров, то а выражается как сумма двух подобных членов, различающихся величинами Wо и В.

При постоянной температуре уравнение принимает вид

Где С в О могут быть рассчитаны из изотерм адсорбции и превращены в величины Wо и В. Дубинин использовал этот метод для получения характеристик образца силикагеля, содержащего микропоры с диаметрами в интервале 20—40 А. Указанный метод еще дорабатывается [7].

Адсорбаты, различающиеся по размеру молекул. Такие адсорбаты можно использовать при исследовании путем построения /-кривых для того, чтобы получить распределение микропор по размерам. Михаил и Шебл [175] использовали такие вещества, как вода, метанол, пропанол, бензол, гексан и тетрахлорид углерода. Различия в получаемых данных связывались с размером пор образца кремнезема, а также со степенью гидроксилирования его поверхности. Молекулы большей части перечисленных адсорбатов не подходят для измерения поверхностей кремнеземов, содержащих тонкие поры [176].

Бартелл и Бауэр [177] еще раньше выполнили исследования с этими парами при температурах 25, 40 и 45°С. Фу и Бартелл [178], применяя метод свободной поверхностной энергии, определяли величину поверхности с использованием в качестве адсорбатов различных паров. Они нашли, что значения поверхностей в этом случае в общем согласовывались со значениями, определенными по адсорбции азота.

Для измерения поверхности в твердых материалах, содержащих микропоры такого размера, который затруднял проникновение в них относительно больших молекул азота, может быть использована вода. МП-метод, или «скорректированный метод модельных пор», был применен авторами работы [179] при изучении гидратированного силиката кальция.

Другим способом определения микропористых характеристик является проведение измерений при относительных давлениях вблизи насыщения [180]. Различия в адсорбционных объемах показывают, что такой объем и размер пор не позволяют большим выбранным молекулам адсорбата проникать в них, в то время как наименьшие используемые молекулы, такие, например, как молекулы воды, обнаруживают «полное» проникновение в эти поры, определяемое адсорбционным объемом.

Когда микропоры оказываются слишком малыми, чтобы в них могли войти молекулы метанола или бензола, тогда они еще в состоянии поглощать воду. Высоцкий и Поляков [181] описали такой тип силикагеля, который приготовлялся из кремневой кислоты и дегидратировался при низкой температуре.

Грег и Лангфорд [182] разработали новый подход, так называемый метод предадсорбции, для определения микропор в углях в присутствии мезопор. Сначала проводили ‘адсорбцию нонана, который проникал в микропоры при 77 К, затем откачивали его при обычной температуре, однако микропоры оставались заполненными. После этого методом БЭТ по азоту обычным образом измеряли поверхность образца, причем результаты такого определения согласовывались с геометрически измеренной поверхностью, которую находили методом электронной микроскопии. Подобный метод предадсорбции для исследования микропор, без сомнения, может быть использован применительно к кремнезему, но в таком случае, вероятно, должен использоваться значительно более полярный адсорбат с целью блокирования микропор, такой, например, как деканол.

Рентгеновское рассеяние под малыми углами. Риттер и Эрих [183] использовали данный метод и сравнили полученные результаты с данными адсорбционных измерений. Лонгмен и др. [184] сравнили метод рассеяния с методом вдавливания ртути. Еще раньше возможности этого метода были описаны Порай-Кошицем и др. [185], Породой [186а] и Имеликом, Тейчнером и Картеретом [1866].

Метод вдавливания ртути. Ртуть не смачивает поверхность кремнезема, и требуется приложить высокое давление, чтобы заставить жидкую ртуть войти в поры небольших размеров. Вашбурн [187] вывел уравнение

Где р — равновесное давление; а — поверхностное натяжение ртути (480 дин/см); 0 — краевой угол смачивания между ртутью и стенкой поры (140°); гр — радиус поры.

Из этого уравнения следует, что произведение ргр = 70 ООО в случае, если р выражено в атмосферах, а гР — в ангстремах. В поры радиусом 100 А ртуть способна проникать при давлении выше 700 атм. Следовательно, для проникновения ртути в микропоры необходимо применять очень высокие давления.

Одна из проблем заключается в том, что если силикагель не очень прочен, то структура образца разрушается под воздействием внешнего давления ртути еще до того, как ртуть сможет проникнуть в тонкие поры. Именно по этой причине для исследовательских целей метод измерения адсорбционных изотерм азота предпочтителен. Тем не менее для прочных твердых тел, подобных промышленным кремнеземным катализаторам, метод ртутной порометрии является гораздо более быстрым не только с точки зрения проведения самого эксперимента, но и для обработки данных с целью построения кривых распределения пор по размерам.

Коммерческие ртутные порозиметры широко доступны, а усовершенствованные варианты данного метода описаны в работах [188, 189]. Де Уит и Шолтен [190] сравнили результаты, полученные методом ртутной порометрии, с результатами методов, основанных на адсорбции азота. Они пришли к заключению, что метод вдавливания ртути вряд ли может использоваться при исследовании пор, диаметр которых меньше 10 нм (т. е. радиус меньше 50 А). В случае прессованного порошка аэросила радиус пор, определенный по вдавливанию ртути, в максимуме кривой распределения оказался равным около 70 А, тогда как метод адсорбции азота давал значения 75 и 90 А при расчете кривой распределения разными методами. Расхождение может быть обусловлено искривленным мениском ртути радиусом около 40 А, имеющим более низкое (почти на 50 %) поверхностное натяжение, чем в случае контакта ртути с плоской поверхностью. Согласно Цвейтерингу [191], наблюдается превосходное согласие между указанными методами, когда диаметр пор имеет величину около 30 нм. Подробное описание работы на коммерческом ртутном порозиметре (или пенетрометре), введение необходимых поправок и собственно метод расчета размеров пор представили Фревел и Крессли [192]. Авторы дали также теоретические порозиметрические кривые для случаев разных упаковок однородных по размеру сфер.