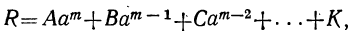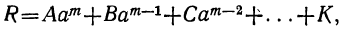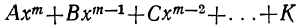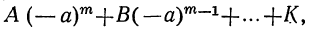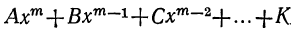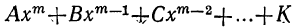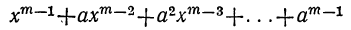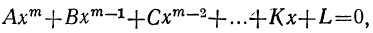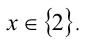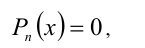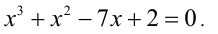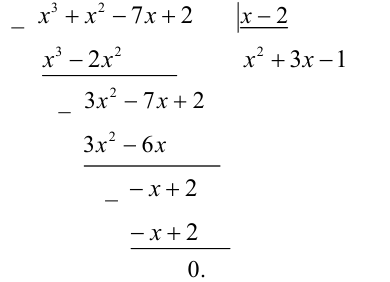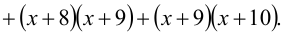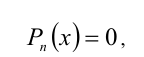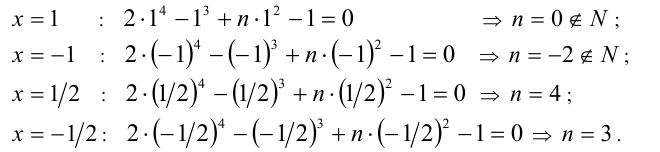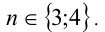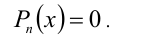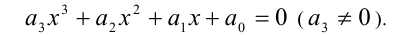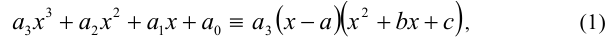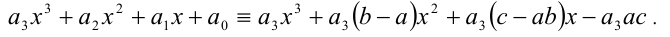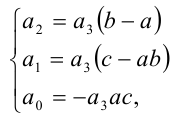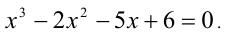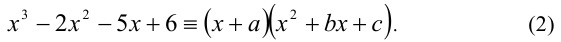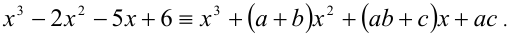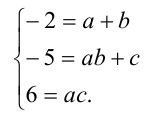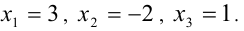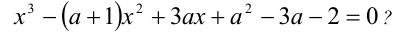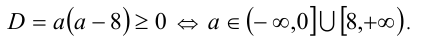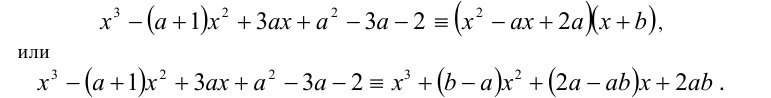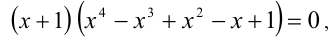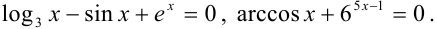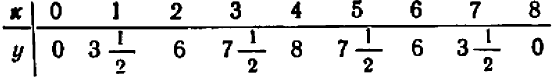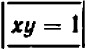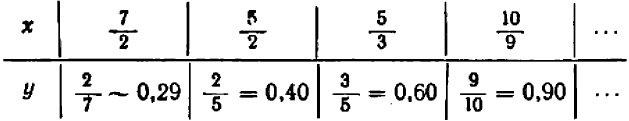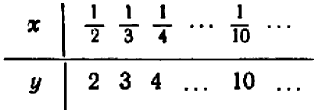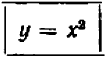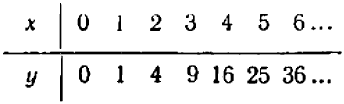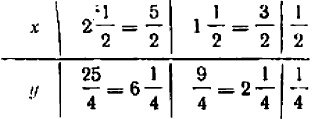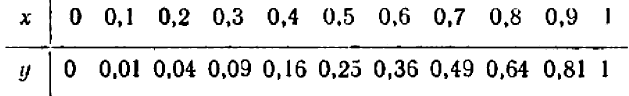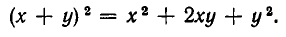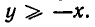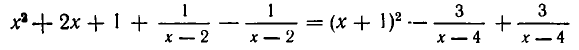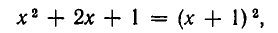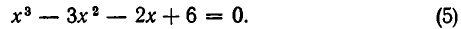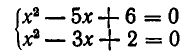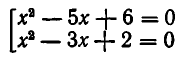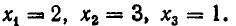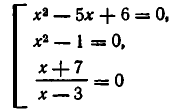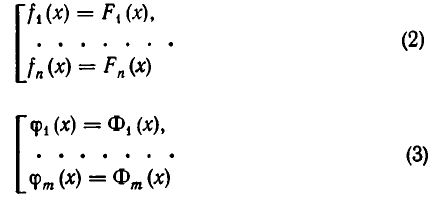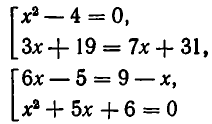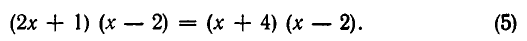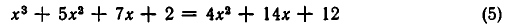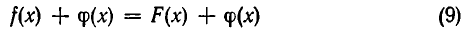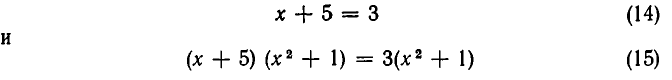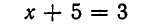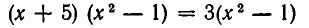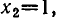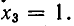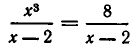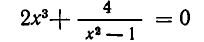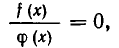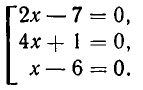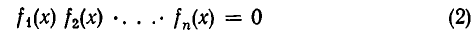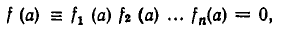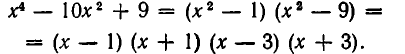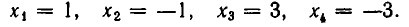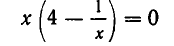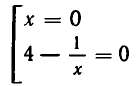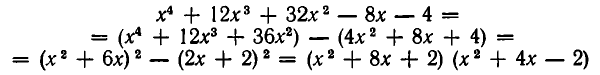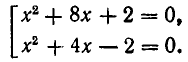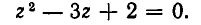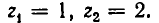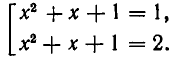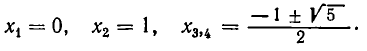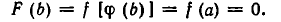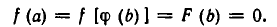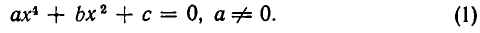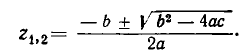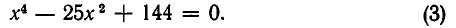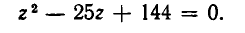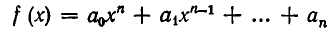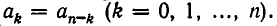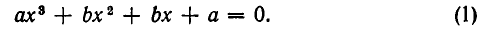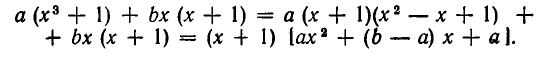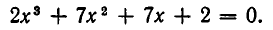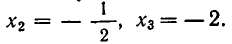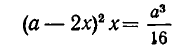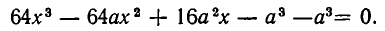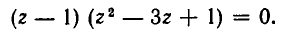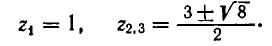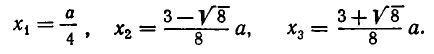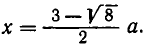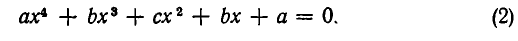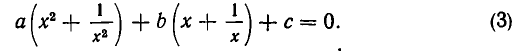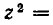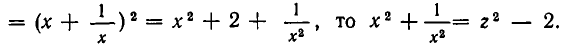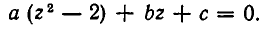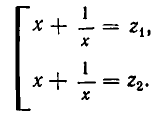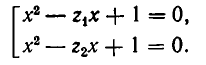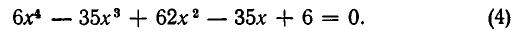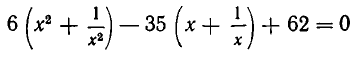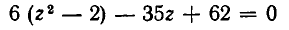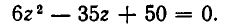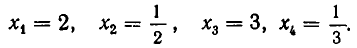Общие методы решения алгебраических уравнений

Разделы: Математика

Уравнения занимают значительное место в курсе математики средней школы. Остановимся лишь на алгебраических уравнениях, которые разобьем на три группы:

1. полиномиальные уравнения вида P_n(x) = 0, где P_n(x) — многочлен n-й степени относительно x;
2. дробно-рациональные уравнения, т.е. содержащие в качестве двух компонент частные двух многочленов;
3. иррациональные уравнения.

Для ряда приемов даны небольшие теоретические обоснования. Приведено 30 приемов, иллюстрированных более чем 36 примерами. Не надо думать, что приведенный в конкретном примере прием является наиболее рациональным для решения данного примера. Просто надо принять к сведению существование такого подхода к решению уравнений.

Одни и те же подходы (применение тригонометрии, использование однородности, разложение на множители и др.) находят применение не только при решении рациональных, дробно-рациональных, иррациональных уравнений, но и при решении трансцендентных уравнений, неравенств, систем.

При написании использовалась литература:

1. Рывкин А. А. «Справочник по математике» – М.: Высшая школа, 1987.
2. Цыпкин А. Г. «Справочник по методам решения задач по математике» – М.: Наука, 1989.
3. Шарыгин И. Ф. Факультативный курс по математике – М.: Просвещение, 1989.
4. Сборник задач по математике для поступающих во ВТУЗы / Под ред. Сканави М. И. – Мн.: Вышэйшая школы, 1990.

В этих пособиях можно найти достаточное количество нужных уравнений, конечно, не пренебрегая другими источниками.

1. Докажем теорему: Если уравнение a_nx n + a_n–1x n–1 + … + a₁x + a₀ = 0 (*) с целыми коэффициентами имеет рациональный корень, где p и q взаимно просты, то a₀ делится на p, а a_n делится на q.

Доказательство: Заменим в (*) x на , получим верное числовое равенство умножим обе части равенства на q n :

Правая часть делится на q, значит, и левая должна делиться на q, но т.к. p и q взаимно просты, то p n не делится на q, но тогда a_n должно делиться на q, иначе левая часть не будет кратна q.

Правая часть кратна p, значит, и левая кратна p, но q n взаимно просты с p, значит a₀ кратно p. Теорема доказана.

Доказательство: Делимое равно делителю, умноженному на частное, плюс остаток. Так как делитель — многочлен первой степени, то остаток будет многочленом, степень которого меньше степени делителя, значит, остаток – const. Частное будет многочленом степени n – 1. Тогда

При x = a это равенство имеет вид

из которого следует P(a) = R. Теорема доказана.

Следствие: Если x = a — корень многочлена, то многочлен делится на x – a без остатка.

Доказательство: При x = a равенство (***) примет вид 0 = 0 + R, из которого следует, что R = 0. А так как остаток от деления равен нулю, то утверждение доказано.

Пример 1. Решить уравнение 30x 4 + x 3 – 30x 2 + 3x + 4 = 0.

Составим различные несократимые дроби, числители которых — делители свободного члена, т.е. 4, а знаменатели — делители старшего коэффициента, т.е. 30.

В левом столбике в знаменателях участвуют все делители числа 30. Видно, что – 1 — корень многочлена. По следствию из теоремы Безу делим многочлен на x + 1

Для поиска корней многочлена 30x 3 – 29x 2 – x + 4 воспользуемся таблицей дробей. При многочлен примет вид Значит, — корень многочлена.

2. При решении алгебраических уравнений может быть полезен метод неопределенных коэффициентов.

Пример 2. Решить уравнение x 4 + 2x 3 – 16x 2 + 11x – 2 = 0.

Пусть многочлен представим в виде произведения

где a , b , g , a, b, c коэффициенты, которые желательно подобрать так, чтобы после раскрытия скобок и приведения подобных слагаемых получился исходный многочлен. Раскроем скобки, полагая, что a = a = 1.

Положим c = 1, g = – 2 или c = 2, g = – 1 (подбираем коэффициенты).

b = – 3, тогда b = 5.

Убедимся, что b = 5, g = – 2, b = – 3, c = 1. Такой набор удовлетворяет всем четырем уравнениям, поэтому можем записать

Решив квадратные уравнения, получим корни исходного уравнения.

Ответ:

3. Решение возвратных уравнений

После почленного деления на x k , они решаются подстановкой

Пример 3. Решить уравнение 2x 4 – 3x 3 – 7x 2 –15x + 50 = 0.

Разделим на x 2 , получим

Уравнение примет вид:

Если l = 1, то уравнение вида ax 2k + bx 2k–1 + cx 2k–2 + dx 2k–3 + … + dx 3 + cx 2 + bx + a = 0 называется возвратным (или симметрическим) уравнением степени 2k первого рода.

Пример 4. Решить уравнение 5x 4 + 3x 3 – 16x 2 + 3x + 5 = 0.

Разделим почленно на x 2 . Имеем .

Ответ:

Если l = – 1, то получим уравнение вида

ax 2k + bx 2k–1 + cx 2k–2 + dx 2k–3 + … + dx 3 + cx 2 – bx + a = 0, которое называется возвратным (или симметрическим) уравнением степени 2k второго рода. Решается подстановкой

Пример 5. Решить уравнение 8x 4 – 42x 3 + 29x 2 + 42x + 8 = 0.

Ответ:

Возвратное уравнение нечетной степени имеет корень – 1. Это объясняется тем, что уравнение имеет четное число членов, которые при замене x на – 1 попарно уничтожаются. Поэтому в начале делят многочлен на x + 1, а частное приведет к возвратному уравнению четной степени, решение которого уже рассмотрено.

Пример 6. Решить уравнение 24x 5 + 74x 4 – 123x 3 – 123x 2 + 74x + 24 = 0.

Имеем возвратное уравнение 5-й степени. Один из его корней – 1. После деления на x + 1, получим

24x 4 + 50x 3 – 173x 2 + 50x + 24 = 0

Ответ:

если , то

По биному Ньютона

Замечание 2. Определить по внешнему виду, что уравнение является возвратным не всегда просто, особенно, если . Поэтому в уравнении степени 2n производим почленное деление на x n и, если при этом получается сумма выражений вида , где n = 0, 1, 2 … m, то дальнейшее решение ясно.

Видео:Решение алгебраических уравненийСкачать

Алгебраические уравнения в математике с примерами решения и образцами выполнения

Алгебраическое уравнение — это уравнение вида. где. — многочлен от переменных. , которые называются неизвестными.

Видео:Общие методы решения уравнений | Алгебра 11 класс #26 | ИнфоурокСкачать

Делимость многочлена

Делимость многочлена, целого относительно х, на разность x— а.

Теорема Безу:

Многочлен, целый относительно х: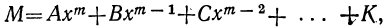
,
при делении на разность х — а (где а есть произвольное число, положительное или отрицательное) даёт остаток

равный тому значению делимого, которое оно получает при х=а.

Доказательство:

Из процесса деления многочлена, расположенного по убывающим степеням буквы х, видно, что деление такого многочлена на х — а можно продолжать до тех пор, пока высший член остатка R не будет содержать в себе буквы х. Пусть при этом частное будет некоторый многочлен Q. Тогда мы можем написать равенство:
M=(x- a)Q+R.

Равенство это есть тождество, т. е. оно верно при всевозможных значениях буквы х, а потому оно должно быть верно и при х-а. Но при x=а оно даёт
M’ = (α — α) Q’ + R
если буквами М‘ и Q‘ обозначим те значения M и Q, которые эти многочлены принимают при х=а (остаток R, как не содержащий вовсе x, не изменится от подстановки а на место х). Так как a — α=0, то и произведение (а — a) Q‘ равно 0; значит, последнее равенство даёт M‘= R, т. е.

что и требовалось доказать.

Следствие:

Так как x+α=x— (—а), то, применяя доказанную теорему к сумме х+а, найдём:
многочлен

при делении на сумму x+α даёт в остатке число, равное

т. е. число, равное тому значению делимого, которое оно получает при x= —а.

Примеры:
1) Многочлен x⁵—3x²+5x—1 при делении на х—2 даёт остаток, равный
2⁵-3 ∙ 2²+5 ∙ 2—1=29.

2) Многочлен x⁵—3x²+5x—1 при делении на x+2 даёт остаток
(-2)⁵-3 (- 2)²+5 (-2)—1=-55.

Следствие:

Для того чтобы многочлен

делился на разность х—а, необходимо и достаточно, чтобы при х=а он обращался в нуль.

Это необходимо, так как если указанный многочлен делится на x—а, то остаток от деления должен быть нуль, а этот остаток, по доказанному выше, есть то значение делимого, которое оно принимает при x=а. Это и достаточно, так как если многочлен обращается в нуль при x=a, то это значит, что остаток от деления этого многочлена на х—а равен нулю.

Следствие:

Для того чтобы многочлен

делился на сумму х+а, необходимо и достаточно, чтобы при х = —а он обращался в нуль, так как сумма х+а есть разность x—(— а).

Примеры:
1) Многочлен x³-4x²+9 делится на х—3, потому что
З³ — 4∙3²+9=0.
2) Многочлен 2x²+x-45 делится на x+5, так как
2 (-5)²+(-5)—45=0.

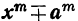
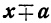
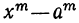
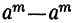
Делимость двучлена на . 1) Разность одинаковых степеней двух чисел делится на разность тех же чисел, так как при делении на х—а даёт остаток , т. е. 0.

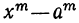
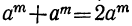
2) Сумма одинаковых степеней двух чисел не делится на разность этих чисел, так как при делении на х—а даёт остаток , а не 0.

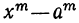
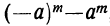
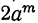
3) Разность одинаковых чётных степеней двух чисел делится, а нечётных не делится на сумму этих чисел, так как при делении разности , на х+а остаток равен , что при m чётном равно нулю, а при tn нечётном составляет — .

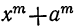
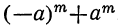
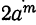
4) Сумма одинаковых нечётных степеней двух чисел делится, а чётных не делится на сумму этих чисел, так как. при делении суммы на x+α остаток равен что при m нечётном равно 0, а при m чётном составляет .

Примеры:
1) x¹+α¹ делится на x+α, но не делится на х—а.
2) x²- α² делится и на х—а, и на x+a.
3) x²+α² не делится ни на х—а, ни на x+a.
4) x³- α³ делится на х—а, но не делится на x+α.
5) x³+α³ делится на x+a, но не делится на х—а.

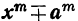
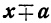
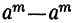
Частные, получаемые при делении на . Если произведём деление двучлена на двучлен х—а, то в частном получим многочлен:

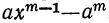
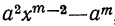
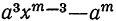
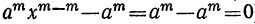
(остатки при этом делении идут в такой последовательности: 1-й остаток , 2-й остаток , 3-й остаток ,…, m-й остаток ).

Очевидно, что многочлен, получившийся в частном, содержит m членов; сумма показателей в каждом члене при а и х одна и та же, именно: m—1; показатели х идут, уменьшаясь на 1,от m—1 до 0, показатели же а идут, увеличиваясь на 1, от 0 до m—1; коэффициенты у всех членов равны 1; знаки все +; число членов в частном m.

Заметив это, можем прямо писать:
x³- α³=(x-a) (x²+αx+α²);
x⁴- α⁴=(x-α) (x³+αx²+α²x+ α³);
x⁵ — α⁵=(x-a) (x⁴+αx3+α²x²+α³x+α⁴) и т. п.

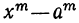
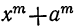
Чтобы получить частное от деления на x + a при m чётном или при делении на x+a при m нечётном, достаточно в полученном выше частном заменить а на —а. Таким образом:
x³+α³=(x+α) (x²-αx+α²);
x⁴—α⁴=(x+α) (х³-αx²+α²x-α³);
x⁵+a⁵=(x+α) (х⁴ — αx³+α²x² — a³x+a⁴) и т.п.

Видео:11 класс, 27 урок, Общие методы решения уравненийСкачать

Общий вид алгебраического уравнения

Мы ранее видели, что уравнение, содержащее неизвестное в знаменателях, может быть приведено к целому виду. Далее мы знаем, что уравнение, содержащее неизвестное под знаком радикала, может быть приведено к рациональному виду. Вследствие этого можем сказать, что всякое уравнение, в котором неизвестное связано с данными числами посредством конечного числа шести алгебраических действий (сложения, вычитания, умножения, деления, возвышения в степень и извлечения корня), может быть приведено к такому целому и рациональному виду:

где коэффициенты А, В, С, … , K и L суть постоянные вещественные или комплексные числа, а m есть показатель степени уравнения. Некоторые коэффициенты, кроме первого, в частных случаях могут равняться нулю.

Уравнение такого вида называется алгебраическим. Алгебраические уравнения степени выше второй называются уравнениями высших степеней.

Видео:Решение системы уравнений методом ГауссаСкачать

Некоторые свойства алгебраического уравнения

Уравнения высших степеней составляют предмет высшей алгебры. Элементарная же рассматривает только некоторые частные виды этих уравнений.

Высшая алгебра устанавливает следующую важную теорему:
Всякое алгебраическое уравнение имеет вещественный или комплексный корень (теорема Гаусса 2), 1799 г.).

Допустив эту истину (доказательство которой в элементарной алгебре было бы затруднительно), нетрудно показать, что:
Алгебраическое уравнение имеет столько корней, вещественных или комплексных, сколько единиц в показателе его степени.

Действительно, согласно теореме Гаусса, уравнение
(1)
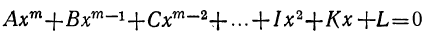
имеет вещественный или комплексный корень; пусть этот корень будет а. Тогда многочлен, стоящий в левой части уравнения (1), должен делиться на х—а. Если произвести это деление, то в частном получим многочлен степени m—1, у которого первый коэффициент будет А. Обозначив другие его коэффициенты соответственно буквами B₁, C₁ ,…, K₁ и приняв во внимание, что делимое равно делителю, умноженному на частное, можем представить уравнение (1) так:
(2)
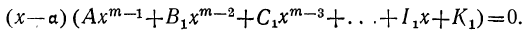
Приравняв нулю многочлен, стоящий во вторых скобках, получим новое уравнение, которое по той же теореме должно иметь некоторый корень β; вследствие этого левая его часть может быть разложена на два множителя: х—β и многочлен степени m—2, у которого первый коэффициент по-прежнему будет А. Поэтому уравнение (1) можно переписать так:
(3)

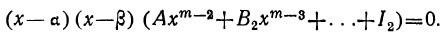
Продолжая эти рассуждения далее, дойдём, наконец, до того, что многочлен, заключённый в последних скобках, будет второй степени, причём первый его коэффициент останется А. Разложив этот трёхчлен на множители, приведём уравнение (1) к виду:
A(x- а) (х—β) (х— γ) . .. (х—λ)=0, (4)
где всех разностей: x-a, х- β,…, будет m. Очевидно, что уравнение (4) обращается в тождество при каждом из значений: x=α, x=β, x=γ, . x=λ и не удовлетворяется никакими иными значениями x (если A≠0); значит, уравнение (1) имеет m корней: a, β, γ ,…, λ. В частных случаях некоторые корни могут оказаться одинаковыми.

Полезно заметить ещё следующие истины, доказываемые в высшей алгебре.

Сумма корней всякого алгебраического уравнения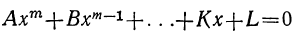
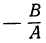
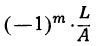
равна , а произведение корней равно (примером может служить квадратное уравнение).

Если алгебраическое уравнение с вещественными коэффициентами имеет комплексные корни, то число этих корней — чётное (примером может служить биквадратное уравнение).

Если алгебраическое уравнение с вещественными коэффициентами имеет n корней вида p+qi, оно имеет ещё n корней вида p—qi (примером может служить биквадратное уравнение, комплексные корни которого всегда сопряжённые), и так как
[х—(p+qi)][x-(р— qi)]=[(x-p)- qi] (x-p)+qi] =
=(х—р)²—q²i²=(x-p)²+q²=x²-2 +(p²+q²),
то левая часть уравнения содержит в этом случае n вещественных множителей вида ax²+bx+c.

Алгебраическое уравнение нечётной степени с вещественными коэффициентами имеет, по крайней мере, один вещественный корень.

Уравнения с произвольными буквенными коэффициентами степени не выше четвёртой разрешены алгебраически, т. е. для корней этих уравнений найдены общие формулы, составленные из коэффициентов уравнения посредством алгебраических действий.

В этом смысле уравнения с произвольными коэффициентами степени выше четвёртой не могут быть разрешены алгебраически (теорема Абеля); однако, если коэффициенты уравнения какой угодно степени выражены числами, всегда есть возможность вычислить с желаемой степенью приближения все его корни как вещественные, так и мнимые. Способы такого вычисления излагаются в высшей алгебре.

Видео:Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать

Методы решения целых алгебраических уравнений

Разложение на множители

Часть целых алгебраических уравнений 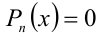(или аналогичных неравенств) степени n выше 2-й могут быть решены путём разложения многочлена в левой части уравнения (неравенства) на множители с помощью таких известных приёмов, как группировка и вынесение общего множителя за скобки. Иногда для достижения цели приходится прибавлять и одновременно вычитать одно и то же выражение. Отметим, что порой разложение на множители этим способом требует определённого искусства.

Если разложение на множители удалось выполнить, то решение алгебраического уравнения сводится к решению совокупности нескольких уравнений, но более низкой степени. Неравенство после разложения на множители можно решать методом интервалов.

Пример:

Решить уравнение

Решение:

Из 1-го уравнения находим корни 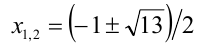, а второе не имеет решений.

Пример:

Найти все положительные корни уравнения

Решение:

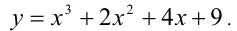
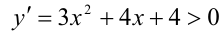
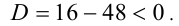
Покажем, что второе уравнение в совокупности не имеет положительных решений. Действительно, рассмотрим функцию Её производная при всех действительных x, так как Следовательно, функция всюду монотонно возрастает, при этом y(0) = 5 . Отсюда следует, что при x > 0 её график не пересекает оси абсцисс.

Ответ:

Подбор корня с последующим понижением степени уравнения

При решении алгебраических уравнений и неравенств степени выше второй можно использовать общий принцип последовательного понижения степени уравнения (неравенства).

Пусть требуется решить уравнение n -й степени

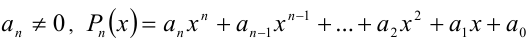
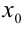
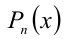
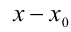
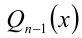
где целый рациональный алгебраический многочлен n -й степени. Если удалось подобрать (любым способом) какой-либо корень данного уравнения, то для нахождения остальных корней уравнения следует поделить многочлен на разность X — Х0 (или целенаправленной группировкой слагаемых, выделяя разность , разложить этот многочлен на множители). В результате деления образуется некоторый многочлен , степень которого на единицу меньше первоначальной. Таким образом, задача свелась к решению алгебраического уравнения степени n — 1 :

Пример:

Решить уравнение

Решение:

Заметим, что x = 2 является корнем данного уравнения. Найдём другие корни этого уравнения:

Решая уравнение 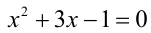, находим ещё два корня

Эта ссылка возможно вам будет полезна:

Пример:

Решить уравнение

Решение:

Легко заметить, проанализировав структуру уравнения, что числа x = 0 и x = -10 являются решениями данного уравнения. С другой стороны, ясно, что это квадратное уравнение, а поэтому может иметь не более двух корней. Так как два корня уравнения уже подобраны, то других корней нет.

В некоторых случаях, для того чтобы не подбирать корень «вслепую», можно воспользоваться следующим методом.

Метод поиска рациональных корней у многочленов с целыми коэффициентами

Для решения такого рода уравнений и неравенств используется метод, в основе которого лежит Теорема 9 из предыдущего пункта. Рассмотрим подробнее суть этого метода. Пусть требуется найти рациональные корни уравнения n -й степени

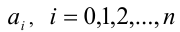
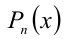
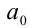
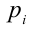
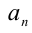
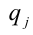
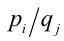
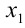
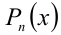
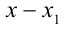
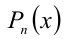
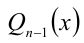
причём все коэффициенты алгебраического многочлена являются целыми числами. Поиск рациона-льных корней можно свести к перебору ограниченного количества вариантов. Для этого необходимо, во-первых, найти все целочислен-ные делители свободного члена (их конечное число, однако если этот коэффициент содержит слишком много делителей, то это затрудняет поиск корней в уравнении). Обозначим, например, эти делители через . Во-вторых, следует найти все натуральные делители старшего коэффициента уравнения . Обозначим эти делители через . В-третьих, надо составить всевозможные дроби вида . Наконец, перебирая по очереди все такие дроби, проверить, является ли в действительности каждая из них корнем данного уравнения. Найдя таким образом первый корень , вы или сразу понижаете степень уравнения делением многочлена на разность , (причём в силу следствия из теоремы Безу обязательно разделится нацело на этот линейный двучлен) и получаете некоторый многочлен степени на единицу меньшей, чем первоначальная. Или, перебирая все дроби, находите все рациональные корни и уже затем понижаете степень уравнения сразу на столько порядков, сколько рациональных корней удалось найти, и ищете оставшиеся иррациональные корни. В любом случае задача сводится к решению уравнения более низкой степени.

Пример:

При каких натуральных n уравнение 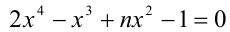имеет рациональные корни?

Решение:

Воспользуемся приведённым выше методом. Свободный член имеет два целочисленных делителя: ± 1, а старший коэффициент — два натуральных делителя: 1,2. Поэтому рациональные корни следует искать среди чисел 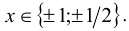Подставим их поочерёдно в уравнение.

Ответ:

Метод неопределённых коэффициентов

Иногда для решения целых алгебраических уравнений (неравенств) с одной или несколькими неизвестными используют метод неопределённых коэффициентов. Пусть, например, решается уравнение

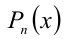
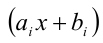
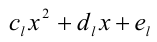
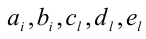
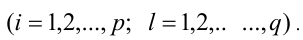
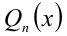
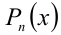
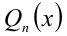
Суть метода состоит в том, что многочлен в левой части уравнения представляется в виде произведения линейных и(или) квадратичных сомножителей с неизвестными (неопределёнными) коэффициентами Чтобы найти эти коэффициенты, раскрывают скобки в указанном произведении и приводят образовавшийся при этом многочлен к стандарт-ному виду. Так как два многочлена и одной степени тождественно равны тогда и только тогда,

когда равны коэффициенты при одинаковых степенях переменной x, то, приравнивая эти коэффициенты, получают систему уравнений относительно неизвестных коэффициентов. Эту систему решают (или подбирают любое решение). Найденные таким способом коэффи-циенты 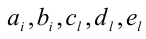становятся определёнными и их значения подставляются в исходное разложение. К недостаткам метода можно отнести то, что получаемая система уравнений для нахождения коэффициентов может оказаться громоздкой и трудной даже в подборе решения.

Рассмотрим применение этого метода на примере решения кубического уравнения. Допустим, требуется решить уравнение

Известно, что многочлен третьей степени всегда можно представить в виде произведения многочленов первой и второй степеней. Таким образом, сразу для всех действительных значений переменной x должно выполняться равенство

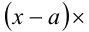
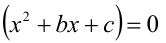
где числа а,b,c являются в данном случае искомыми неопределён-ными коэффициентами. Найдём их значения. После этого останется подставить их в правую часть (1) и, приравняв её к нулю, решить уравнение для нахождения всех корней уравнения.

Чтобы найти коэффициенты а,b,c, раскроем скобки в правой части тождества (1) и приведём образовавшийся при этом многочлен к стандартному виду

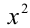
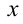
Многочлены третьей степени тождественно равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях x . Приравнивая коэффициенты при , и свободные члены, получаем систему трёх алгебраических уравнений относительно трёх неизвестных а,b,c :

решая которую (можно даже просто подобрать любое решение этой системы) находим коэффициенты.

Пример:

Решить уравнение

Решение:

Воспользуемся для решения методом неопределённых коэффициентов. Будем искать разложение многочлена, стоящего в левой части уравнения, в виде

Раскрыв скобки, приведём многочлен в правой части к стандартному виду

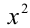
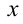
Приравнивая коэффициенты слева и справа при ,и свободные члены, получаем в итоге систему трёх уравнений с тремя неизвестными коэффициентами а,b,c:

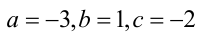
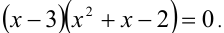
Найдя подбором решение подставим найденные коэффициенты в разложение (2). Таким образом, исходное уравнение приобретает вид Оно имеет три корня

Пример:

При каких значениях а все корни уравнения 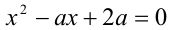являются корнями уравнения

Решение:

Чтобы первое из уравнений имело корни, необходимо, чтобы его дискриминант был неотрицателен, т.е.

Далее, второй многочлен в силу теоремы Безу должен делиться нацело на первый многочлен. Иными словами, должно найтись такое b , что при всех действительных x справедливо тождество

Для нахождения неопределённых коэффициентов (в данном случае в их роли выступают а и b ) воспользуемся известным фактом, что два кубических многочлена, стоящие по разные стороны от знака равенства, тождественно равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях переменной x . Приравнивая эти коэффициенты, получаем систему уравнений

Метод умножения на функцию

Иногда, применяя приём умножения обеих частей уравнения (неравенства) на некоторую функцию, удаётся упростить уравнение (неравенство).

Пример:

Решить уравнение

Решение:

Заметим, что x = — 1 (и вообще никакое отрицательное число) не является корнем данного уравнения. Домножим обе части данного уравнения на выражение (х +1). Получаем уравнение-следствие

множество решений которого состоит из всех решений исходного уравнения и числа x = -1. Это число является посторонним корнем, возникшем как раз в результате умножения уравнения на функцию, имеющую действительный нуль. Применяя известную формулу сокращенного умножения, получаем существенно более простое уравнение 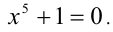Поскольку уравнение не имеет других решений, кроме x = -1, то приходим к ответу.

Ответ: уравнение не имеет решений.

Рассмотрим некоторые виды целых алгебраических уравнений, решаемые в основном при помощи специально подобранных подстановок.

Понятие алгебраического и трансцендентного уравнения и методов их приближенного решения

Введем понятия алгебраического и трансцендентного уравнения.

Алгебраическое уравнение — уравнение, в котором переменная 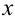находится в основании степени с рациональным показателем.

Примерами алгебраических уравнений могут служить уравнения вида: , .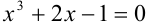

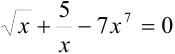
Уравнение, содержащее неизвестную переменную под знаком логарифма, тригонометрических функций, обратных тригонометрических функций или в показателе степени некоторого числа, называется трансцендентным.

Примерами трансцендентных уравнений могут служить уравнения вида:

Решить предложенное уравнение — значит найти все значения переменной 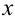, обращающие его в верное тождество (корни уравнения), или доказать, что корней нет.

Из курса алгебры нам известны методы и приемы решения некоторых видов алгебраических и трансцендентных уравнений: например, квадратных уравнений; уравнений, решаемых методом группировки и вынесения за скобки общего множителя. Но даже решение несложного кубического уравнения вызовет у нас определенные сложности. Если нс удастся решить заданное уравнение привычными способами, существуют методы приближенного решения уравнений, состоящие из двух этапов:

1. отделение корней;

2. уточнение корней до заданной степени точности с помощью одного из следующих методов:

Этап отделения корней необходим для того, чтобы определить, какому промежутку принадлежат корни уравнения. На этом этапе обычно используется графический способ.

Пример:

Определить промежуток, которому принадлежат корни уравнения .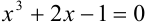

Решение:

Преобразуем данное уравнение к виду: .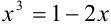

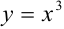
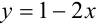
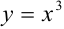
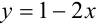
Построим графики функций и (рис. 46.1).

— кубическая парабола, строится по таблице значений:

— прямая, строится по двум точкам:

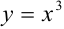
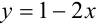
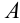
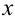
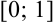
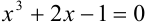
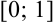
По рисунку видим, что графики функций и пересекаются в единственной точке , координата которой принадлежит отрезку . Следовательно, уравнение имеет ровно один корень на промежутке .

Ответ: .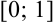

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Другие лекции по высшей математике, возможно вам пригодятся:

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Алгебраические уравнения и их геометрическое истолкование

Уравнение с одной буквой (неизвестным)

Один из основных вопросов, которыми занимается алгебра, заключается в решении уравнений нормального вида. Так называются уравнения, у которых в левой части стоит многочлен, расположенный по степеням неизвестной буквы, а в правой части — нуль.

Степень многочлена в левой части носит название степени уравнения.

Мы встречались не раз с уравнениями, которые не имели нормального вида: таковы, например, уравнения , , .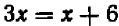

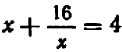
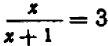
Подобного рода уравнения могут быть приведены к уравнениям нормального вида. Для этого до­ статочно освободиться от дробей, затем перенести на­ лево члены, стоящие в правой части, сделать приведение подобных членов и, наконец, правильно располо­жить члены.

Таким образом, привести заданное уравнение к уравнению нормального вида удается по большей части несложными приемами.

Напротив, нахождение всех корней уравнения представляет собою более трудную задачу, в особенности в том случае, если уравнение высокой степени.

Уравнение первой степени (линейное) имеет вид .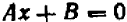

Уравнение второй степени (иначе квадратное) имеет вид .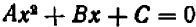

Уравнение третьей степени (иначе кубическое) имеет вид .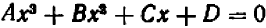

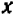
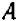
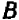
Так можно продолжать и дальше. Ради единообразия неизвестное здесь обозначено буквой ; коэффициенты же , и т. д. — известные числа. В уравнении нормального вида старший коэффициент, конечно, следует считать отличным от нуля.

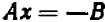
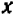
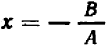
Уравнение первой степени мы решаем (см. гл. 6) следующим образом: свободный член переносим направо , затем делим уравнение на коэффициент при : .

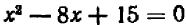
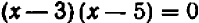
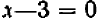
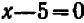
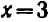
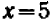
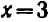
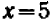
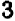
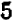
В случае уравнений второй степени или высших степеней решение уравнения тесно связано с разложением левой части на линейные множители. Так, напри­мер, уравнение можно переписать в виде ; далее сошлемся на теорему: если про­изведение двух множителей равно нулю, то непременно один из множителей равен нулю. Поэтому или или ; значит, или или . Обратно, если или , то или первый множитель равен нулю или второй; но в обоих случаях произведение равно нулю, т. е. уравнение удовлетворяется. Итак, уравнение имеет два корня: и .

В отдельных примерах нам удавалось разлагать трехчлен второй степени на линейные множители; более полно общий прием разложения (по ­средствам «выделения квадрата») будет рассмотрен в главе 12.

Что касается уравнений третьей, четвертой и высших степеней, то, не говоря об отдельных частных случаях, разложить их левую часть на множители весь­ма трудно. С другой стороны, очень просто можно составить уравнение, имеющее наперед заданные корни; при этом степень уравнения в точности будет равняться числу корней.

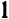
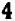
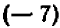
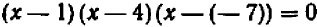
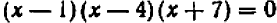
Например, пусть заданы три числа: , и ; тогда уравнение, имеющее эти числа (и только их) своими корнями, таково: , или .

Производя умножение, получаем окончательно: .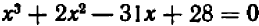

Можно доказать, что число корней уравнения никогда не превышает его степени. Но иногда оно бывает меньше степени уравнения.

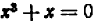
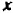
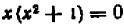
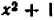
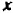
Например, уравнение — третьей степени, но имеет только один корень . Это сразу видно, если в левой части вынести за скобку (здесь второй множитель ни при каком значении не обращается в нуль).

Совокупность точек на числовой оси, являющихся корнями уравнения (иначе, удовлетворяющих этому уравнению), дает нам геометрическое представление этого уравнения.

Уравнение с двумя буквами (переменными)

Нам хорошо известно, что решением (корнем) уравнения с одной неизвестной буквой называется вся­кое значение входящей буквы, удовлетворяющее уравнению.

Если уравнение содержит две неизвестные буквы, понятие решения должно быть обобщено и именно следующим образом: решением уравнения с двумя неизвестными буквами называется пара значений двух неизвестных, удовлетворяющая уравнению.

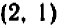
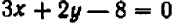
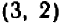
Так, пара чисел есть решение уравнения ; то же можно сказать о паре чисел ; но, например, пара не есть решение.

В случае уравнения с двумя неизвестными найти и перечислить все решения, как правило, невозможно. Уже простейшие примеры, вроде или , показывают, что такое уравнение может иметь бесконечное множество решений.

Поэтому, если в уравнение входят две (или более) неизвестных буквы, их называют обыкновенно не неизвестными, а переменными (переменными величинами).

Алгебраическое уравнение с двумя буквами считается нормальным, если в правой части стоит нуль, а в левой — многочлен, расположенный по обеим бук­вам.

Уравнения с двумя буквами (как и уравнения с од­ной буквой) классифицируются по степеням: степенью уравнения называется степень многочлена, стоящего в его левой части, причем обе буквы считаются главными.

Уравнения первой степени (линейные) имеют вид .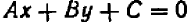

Уравнения второй степени (квадратные) имеют вид .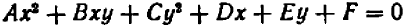

Отдать себе отчет в том, какова совокупность решений данного уравнения, нам помогает геометрическое представление уравнения: оно делает наглядной ту зависимость, которая существует между значениями букв, удовлетворяющими уравнению. Познакомимся ближе с этим геометрическим представлением.

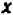
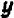
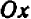
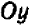
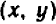
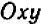
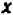
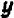
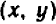
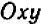
Так как у нас имеется не одна, а две буквы, до­пустим, и из которых каждая может принимать различные значения, то уже нельзя обойтись числовой прямой, а необходимо прибегнуть к числовой (координатной) плоскости. Проведем на листе клетчатой бумаги горизонтальную ось и вертикальную ось масштабы на осях будем брать одинаковые. Каждая пара значений букв изображается, как нам известно, некоторой определенной точкой плоскости , именно — точкой с абсциссой и ординатой . Поэтому совокупность всех пар значений , удовлетворяющих уравнению, изображается также не­ которой совокупностью (геометрическим местом) точек на плоскости . Эта совокупность и дает геометрическое представление решений нашего уравнения; она называется графиком уравнения. Итак, график урав­нения есть совокупность всех тех точек координатной плоскости, координаты которых удовлетворяют уравнению.

Пример:

Рассмотрим уравнение .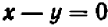
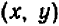
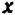
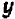
Его графиком является совокупность точек , у ко­торых абсцисса равна ординате легко понять, что все такие точки лежат на биссектрисе первого и треть­ его координатных углов: эта биссектриса и представляет собой график нашего уравнения.

Пример:

Второй пример возьмем более сложный. Пусть нам дано уравнение второй степени: .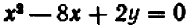

Посмотрим, как можно наметить его график.

Ничего не стоит решить уравнение относительно буквы :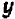

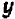
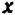
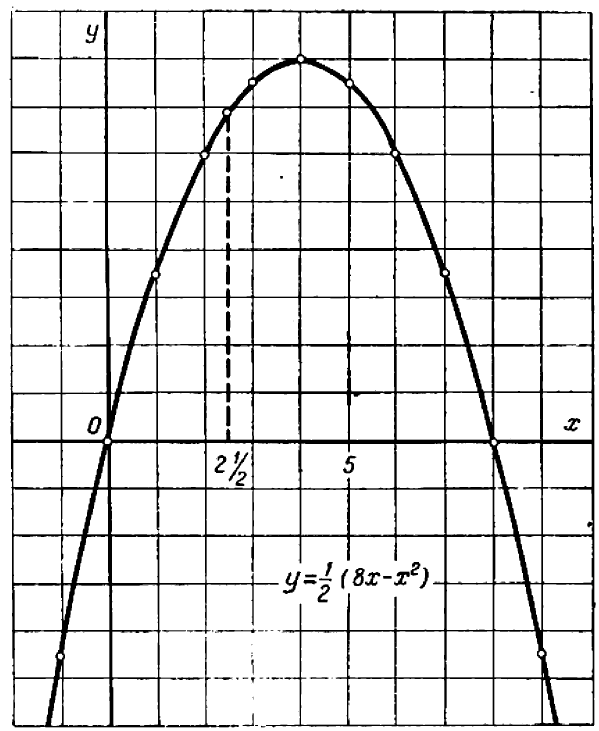
Дальше можно составить табличку числовых значений переменной , соответствующих заранее назначенным значениям переменной :

Черт. 39

Каждую полученную точку сейчас же отмечают на черте­ же. Точки располагаются с известной правильностью.

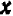
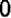
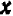
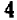
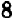
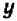
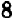
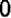
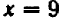
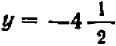
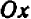
Чертеж 39 показывает, что при возрастании значений от до значения также возрастают от до ; затем при дальнейшем возрастании от до значения убывают от до . При получаем уже отрицательное значение: , придется поставить точку ниже оси .

При получаем ; и еще дальше значения быстро убывают (в алгебраическом смысле).

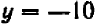
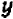
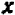
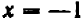
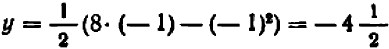
Можно букве давать и отрицательные значения; например, при будем иметь и т. д.

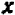
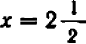
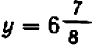
Полезло убедиться, что точки, получающиеся при подстановке дробных значений , не нарушают общей правильности в расположении точек графика (напри­мер, при получаем ).

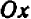
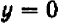
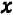
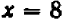
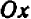
Поставим себе еще и такой вопрос: имеет ли наш график какие-нибудь точки на оси , кроме двух, уже найденных? Чтобы получить ответ, достаточно в уравнении положить и решить полученное уравнение относительно . Мы получаем два корня: и . Иных корней нет. Значит, график пересекается с осью только в двух, уже ранее найденных точках.

Хотя мы отметили на чертеже не свыше десятка точек, положение которых нам известно вполне точно, тем не менее правильность их расположения не оставляет сомнений в том, что все остальные, не отмеченные нами, точки графика лежат на некоторой плавной кривой, проходящей через отмеченные точки.

Эта кривая и есть график нашего уравнения. Провести ее от руки не представит труда.

Правда, полученная таким образом кривая даст возможность лишь приближенно судить о положении тех точек графика, координаты которых не были вычислены.

Использованный нами прием получения графика но­сит название построения графика по точкам.

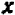
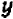
Постараемся дать описание этого приема, не связывая его с каким-либо определенным примером. Пусть дано некоторое уравнение, содержащее буквы и , мы хотим знать, каков его график.

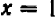
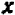
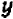
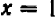
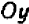
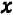
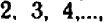
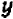
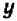
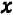
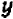
Посмотрим, существуют ли такие точки графика, ко­торые имеют заранее назначенную абсциссу, скажем, . Чтобы ответить на этот вопрос, достаточно под­ставить в уравнение вместо буквы число и решить полученное уравнение (содержащее теперь уже только одну букву) относительно буквы . Корни этого уравнения дают нам ординаты всех точек графика, имеющих абсциссу , т. е. лежащих на одной и той же вертикальной прямой, отстоящей вправо от оси на расстоянии . Продолжая поступать таким же образом, т. е. давая абсциссе другие, заранее назначенные, значения, например, можно найти все точки графика, расположенные на других вертикальных пря­мых. Обыкновенно поступают именно таким образом; при этом стараются облегчить себе работу тем, что предварительно решают данное уравнение относительно буквы , т. е. приводят его к такому виду, чтобы в левой части была одна буква , а правая за­висела только от , но не от , Тогда нахождение то­чек графика сводится к выполнению числовых подста­новок в правой части уравнения.

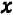
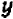
Разумеется, можно было бы также решить данное уравнение относительно буквы и затем придавать ряд значений букве .

Примечание:

Иные уравнения — таковы, что не существует ни одной точки, координаты которой удовлетворяли бы уравнению.
Тогда график отсутствует или представляет собою «пустое место».
Этим свойством обладает, например, уравнение 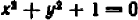которого левая часть всегда положительна.

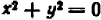
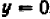
В редких случаях график может оказаться состоящим из одной точки или нескольких точек (в конечном числе). Так, уравнение удовлетворяется только одной парой значений , .

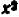
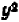
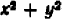
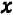
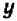
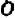
Действительно, каждый из квадратов и может быть или положительным числом, или нулем, но никак не отрицательным числом, сумма же равна нулю только в том случае, если и одновременно равны нулю. Следовательно, весь график сводится к одной точке — началу .

Линейное уравнение с двумя переменными

На чертеже 40 изображен график уравнения 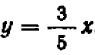(1)

Это — прямая линия, проходящая через начало координат и расположенная в первой и третьей четвертях.

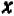
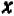
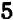
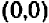
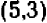
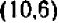
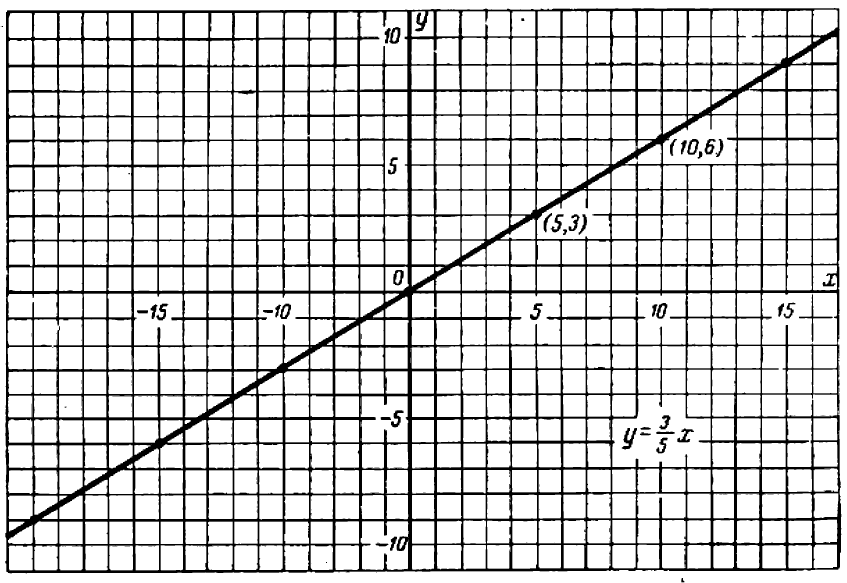
Уравнение показывает, что величина у прямо пропорциональна величине . Желая найти все точки графика с целыми координатами, мы даем букве значения, кратные , и получаем точки: , , и т. д.

Черт. 40

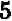
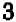
Эти точки отмечены на чертеже. Чтобы перейти от од­ной такой точки к следующей (считая вправо), достаточно отсчитать « клеточек вправо и — вверх».

Коэффициент пропорциональности 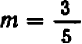позволяет
таким образом, определить направление нашей прямой.

Если бы вместо уравнения (I) было задано, напри­мер, уравнение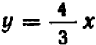
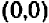
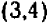
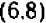
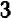
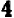
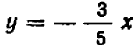
, (2) то мы получили бы точки графика (с целыми координатами): , , и т. д.; отмечая их одну за другой, мы отсчитывали бы « клетки вправо, — вверх», Рассмотрим еще уравнение (3).

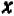
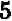
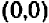
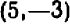
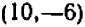
При значениях , кратных , получаем точки: , , и т. д.

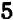
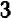
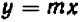
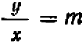
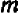
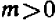
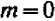
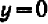
Отсчитывать нужно « клеток вправо и — вниз». Прямая, являющаяся графиком этого уравнения, расположена во второй и в четвертой четвертях. Из наших примеров можно сделать следующие об­щие заключения. Графиком уравнения вида (4) является прямая линия, проходящая через начало . Придавая уравнению вид , мы убеждаемся, что коэффициент пропорциональности представляет собою отношение ординаты любой точки графика к ее абсциссе. Если , то прямая проходит в первой и третьей четвертях; если , то во второй и четвертой. При уравнение принимает вид , и графиком тогда является ось .

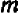
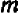
Чем меньше по абсолютному значению, тем более полого расположена прямая (т. е. тем меньше острый угол, образованный ею с горизонтальной осью); напротив, чем больше по абсолютному значению, тем более круто расположена прямая (тем упомянутый острый угол ближе к прямому).

Коэффициент 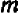в уравнении (4) называется наклоном прямой, являющейся графиком этого уравнения.

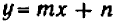
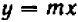
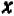
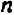
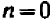
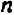
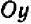
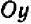
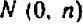
Обратим внимание на то, чем график уравнения отличается от графика уравнения . При каждом данном значении абсциссы соответствующая ордината увеличена на единиц (, или ); значит, получается снова прямая линия, но «сдвинутая» на единиц в направлении оси : она уже не проходит через начало , а пересекает ось в точке .

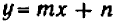
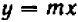
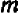
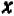
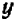
Таким образом, направление прямой то же, что и направление прямой : оно зависит от коэффициента при в уравнении прямой, решенном относительно (называемого и в этом случае наклоном прямой).

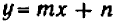
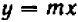
Другими словами, прямые и параллельны.

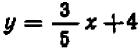
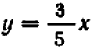
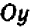
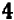
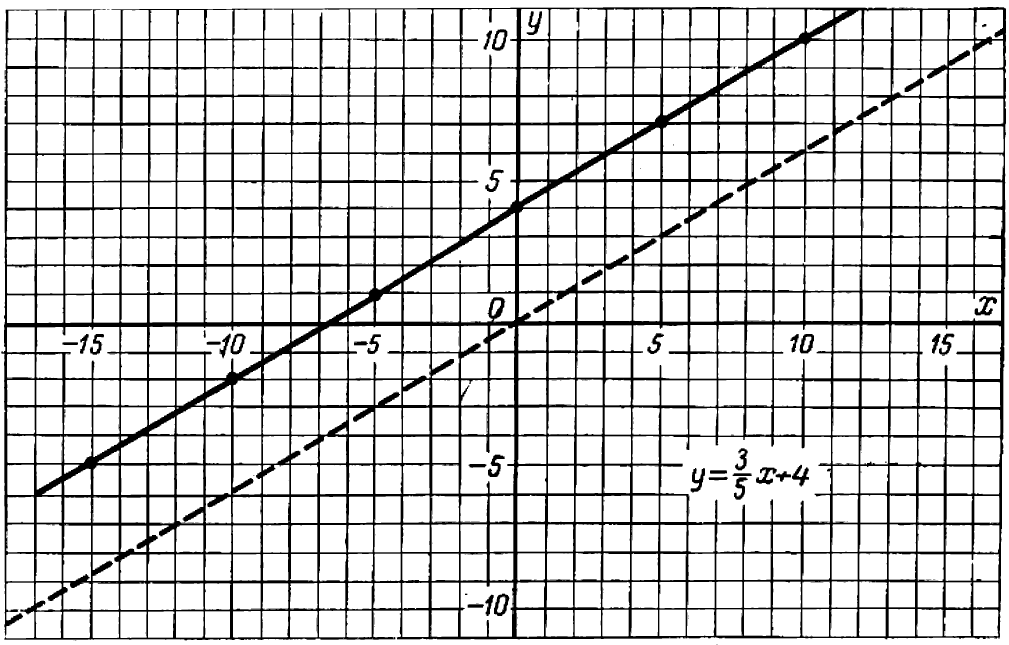
На черт. 41 изображен график уравнения . Это — прямая, параллельная прямой , но образующая на оси отрезок, равный .

Черт. 41

Пусть буква 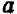обозначает какое угодно число. Постараемся уяснить себе, каков график уравнения .

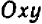
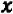
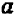
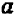
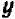
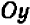
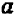
Нам нужно установить, какова совокупность точек на плоскости , координаты которых удовлетворяют уравнению. Уравнение не удовлетворяется, если значение абсциссы не равно ; если же оно равно , то, како­ во бы ни было значение ординаты , уравнение удовлетворяется. Это значит, что уравнению удовлетворяют координаты любой точки на прямой, параллельной оси и отстоящей от этой оси вправо на расстоя­нии .

Итак, уравнение вида имеет графиком прямую, параллельную оси . Точно так же уравнение вида имеет графиком прямую, параллельную оси .

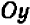
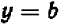
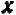
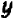
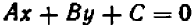
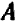
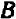
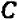
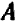
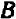
Из предыдущего следует весьма важное заключение: всякое уравнение, линейное относительно буквы и именно, уравнение вида (где , и — постоянные числа, причем и не равны нулю одновременно), имеет своим графиком прямую линию .

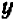
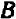
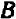
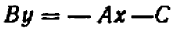
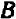
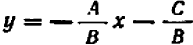
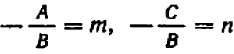
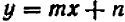
Действительно, если буква на самом деле входит в уравнение (это значит, что не равно нулю), то не представляет труда решить уравнение относительно . Мы получим: и далее, деля все уравнение на , полагая затем
приходим к уравнению вида
, которое, как нам уже известно, изображается прямой линией.

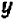
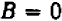
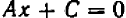
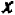
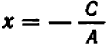
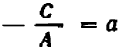
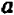
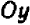
Если же буква отсутствует в уравнении (т. е., если ), то тогда уравнение можно решить относительно буквы (раз , то, по предположе­нию, ), и мы получим: или (где для краткости положено ). Графиком такого уравнения является совокупность точек, имеющих абсциссу ; это также прямая, но уже параллельная оси .

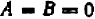
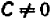
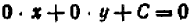
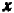
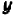
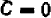
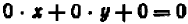
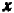
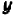
Рассматривать случай, когда не представляет интереса. В этом случае, если , заданное уравнение не удовлетворяется ни при каких значениях и и, значит, гра­фик этого уравнения представляет собою «пустое место»; если же , то напротив, уравнение удовлетворяется при всех значениях и тогда его «график» — вся плоскость.

Раз известно, что линейное уравнение 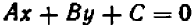изображается прямой линией, то для того, чтобы начертить эту линию на координатной плоскости (на листе клетчатой бумаги), нет необходимости в боль­ших вычислениях.

В самом деле, прямая определяется двумя точками: значит, достаточно сделать две числовые подстановки.

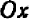
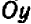
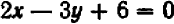
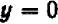
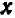
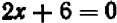
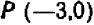
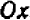
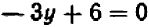
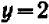
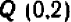
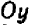
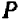
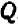
Проще всего установить точки пересечения прямой с осями и . Пусть, например, дано уравнение . Полагая , получим уравнение от­носительно : , из которого следует, что . Таким образом, найде­на точка графика , лежащая на оси . Пола­гая , получим таким же образом: , откуда следует, что . Итак, найдена точка графика , лежащая на оси . Затем остается провести прямую через точки и .

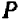
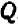
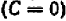
Указанный прием неудобен только в том случае, если точки и находятся очень близко одна от другой, т. е. близки к началу ; он непригоден вовсе, если график проходит через начала . В этих случаях следует делать какие-нибудь другие под­становки.

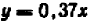
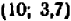
Например, чтобы построить график прямой , заметим прежде всего, что она проходит через начало ; чтобы получить еще одну точку, положим и получим ; итак, прямая проходит через точку .

Нелинейные уравнения с двумя переменными

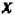
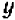
Мы видели, что если заданное уравнение — линейное (т. е. первой степени) относительно букв и , то его график — прямая линия.

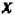
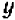
Дальнейшие примеры покажут, что если заданное уравнение — не линейное (т. е. степени второй или выше) относительно букв и , то его графиком являются кривые линии.

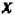
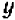
Степень уравнения относительно букв и назы­вается порядком соответствующей кривой.

Мы рассмотрим здесь только несколько наиболее простых и важных примеров кривых, преимущественно второго порядка.

Пример:

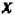
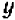
С этим уравнением мы уже встречались. Оно говорит о том, что пе­ременные величины и обратно пропорциональны.

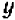
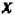
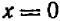
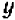
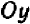
Можно ли решить уравнение относительно ? От­вет — утвердительный, если только имеет значение, не равное нулю. Но легко понять, что при ника­кое значение не может удовлетворить уравнению: это значит геометрически, что на оси нет ни одной точки графика.

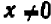
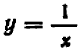
Итак, пусть теперь . Решим уравнение отно­сительно у: .

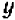
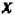
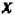
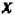
Это равенство свидетельствует, что есть «величи­на, обратная величине ». Посмотрим, как изменится величина, обратная , при изменении самого .

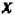
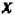
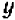
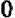
Ограничиваясь пока положительными значениями величины , станем составлять табличку и одновременно отмечать точки на чертеже. Ясно, что с увеличением величина убывает, приближаясь к нулю. Но значения она не принимает.

Попробуем взять и дробные значения :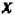

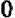
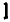
Получающиеся на чертеже точки имеют правильное расположение: через них можно с уверенностью про­ вести плавную кривую. Менее ясно пока, как вести кривую влево, в промежутке от до . Продолжим табличку:

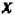
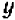
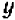
и станем отмечать новые точки. Теперь становится яс­но, что с убыванием положительных значений вели­чина возрастает и притом не ограничено. Имен­но, примет какое угодно большое значение, если только значение будет достаточно малым. Кривая (при движении справа налево) поднимается вверх, примыкая к оси , хотя, как мы видели, с этой осью общих точек не имеет (см. черт. 42).

Черт. 42

Вся полученная кривая расположена в первой четверти. Если бы мы пожелали давать букве 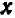отрица­тельные значения, то, составляя соответствующую таблицу и при этом производя деление по известным правилам, получили бы в третьей чет­верти другую «ветвь» кривой.

Обе «ветви». рассматриваемые совместно, обра­зуют кривую, называемую «гиперболой».

Гипербола — кривая второго порядка.

Пример:

Подставляя положительные значения 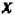, получаем таблицу:

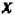
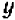
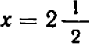
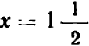
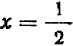
Отметив соответствующие точки на чертеже, мы видим, что при увеличении абсциссы ордината очень быстро возрастает, причем сам график (если попробо­вать его провести) все больше выпрямляется. Напротив, ближе к началу он довольно сильно искривлен. Под­ставляя еще значения , , , мы получим:

В первой клеточке 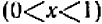сделаем подстановки даже через одну десятую:

Последняя табличка позволяет заключить, что. под­ ходя к началу . график тесно примыкает к оси , касается ее.

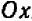
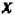
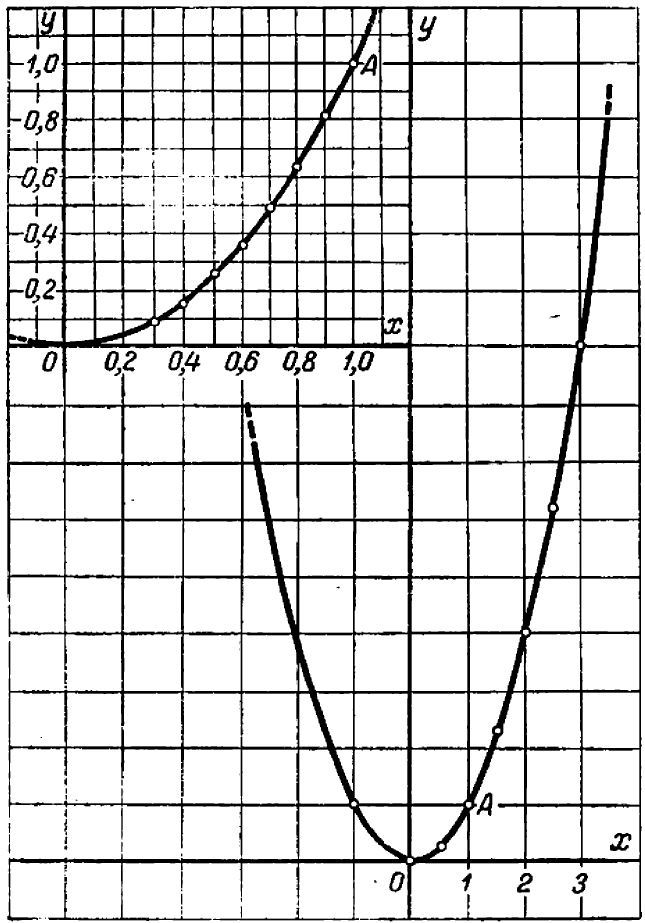
Обращаясь к отрицательным значениям , мы видим, что при возведении в квадрат отрицательного числа знак минус будет уничтожаться. Отсюда ясно, что кри­вая продолжается из первой четверти во вторую симметрично относительно вертикальной оси.

Черт. 43

Полученная кривая носит название параболы(см. черт. 43).

Парабола — кривая также второго порядка.

Пример:

При подстановке больших значений 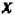, как показы­вает следующая таблица, кубы возрастают гораздо быстрее, чем квадраты:

Напротив, при подстановке значений, близких к нулю, кубы убывают быстрее, чем квадраты:

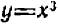
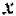
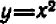
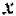
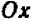
Поэтому кривая с возрастанием подни­мается вверх гораздо круче, чем парабола ; и при убывании до нуля гораздо теснее примыкает к оси .

На параболу 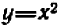эта кривая не похожа еще и в том отношении, что у нее отсутствует вертикальная ось симметрии; но имеется центр симметрии в начале . Это зависит от того, что при возведении в куб отрицательного числа его абсолютное значение возво­дится в куб, но знак остается отрицательный.

Общий вид кривой (кубической параболы) показан на черт. 44.

Черт. 44

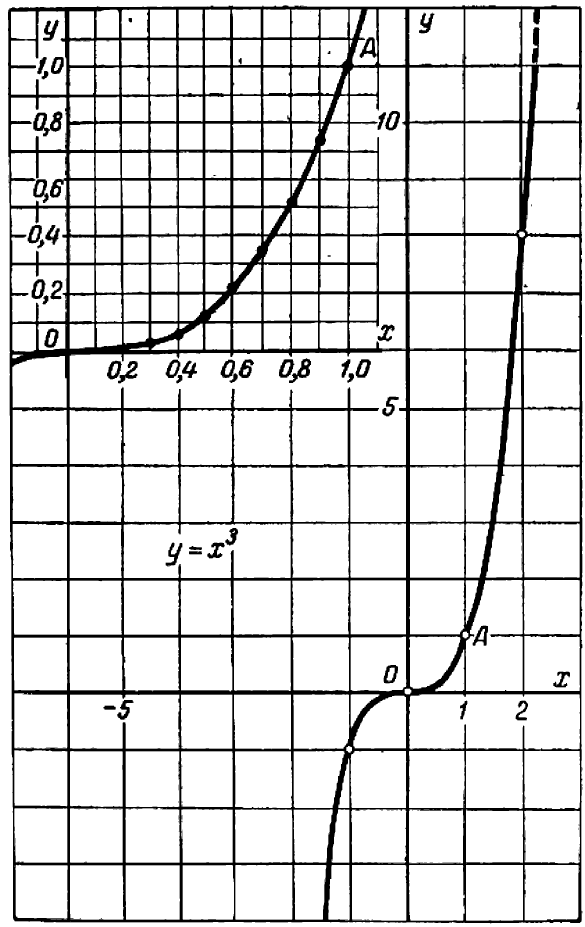
Это — кривая третьего порядка.

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Алгебраические уравнения и алгоритм их решения

Общая теория уравнений

Тождества:

Введем понятие тождественного равенства функ­ций на числовом множестве X.

Пусть функции у = f(х) и у = F(х) имеют области определения А и В соответственно, и X является подмножеством как A, так и В (но не обязательно совпадает с пересечением А и В). Тогда функции у = f(х) и у = F(х) определены на X.

Функции у=f(х) и у=F(х) называются тождественно равны­ми на числовом множестве X, если для любого числа х из X выпол­няется равенство f(х)=F(х). В этом случае говорят, что равенст­во f(х)=F(х) является тождеством на множестве X.

Разумеется, равенство f(х)=F(х) может быть тождеством на некотором множестве X, но не быть тождеством на каком-нибудь другом множестве Y . Рассмотрим, например, функции у=х и у =|x|. На множестве X положительных чисел эти функции тождественно равны: если х — положительное число, то |х|=х. На множестве же Y всех действительных чисел эти функции не явля­ются тождественно равными: при отрицательных значениях х ра­венство

не имеет места, так как при этих значениях |x|= — х.

Совершенно так же определяется понятие тождественного равенства для функций нескольких переменных. Например, функции 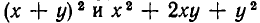переменных х и у тождественно рав­ны на множестве всех значений этих переменных: для любых значе­ний х и у выполняется равенство

Функции же z=х+у и z =|х+у | тождественно равны лишь на множестве пар чисел х, у , для которых 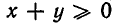или, что то же самое,

Область допустимых значений

Тождественные преобразова­ния многочленов и алгебраических дробей изучались в начальной алгебре, и мы не будем подробно останавливаться на этом вопросе. Разберем лишь вопрос об области допустимых значений функцио­нального равенства. Пусть дано равенство вида

Может случиться, что функции у=f(x) и у=F(x) определены не для всех значений х . Областью допустимых значений аргумента х для равенства (1) мы будем называть множество всех значений х, при которых определены и левая и правая части этого равенства.

Например, для тождества

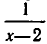
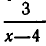
областью допустимых значений является совокупность всех действительных чисел, из которой исключены числа 2 и 4 (при х=2 не определена функция , а при х=4 — функция ).

Следует иметь в виду, что такие преобразования, как приведение подобных членов, могут привести к изменению области допус­тимых значений. Например, тождество (2) справедливо для всех значений х , кроме х=2 и х=4. Если же мы приведем подобные члены, то получим тождество

справедливое для всех без исключения значений х.

Уравнения

Обычно когда даны две функции у=f(х) и у=F(х), то неизвестно, каково множество, на котором эти функ­ции тождественно равны. Поэтому возникает следующая задача: найти все значения х, для которых выпол­няется равенство

При такой постановке задачи (*) называют уравнением с неизвестным х , а все х , при которых функции у=f(х) и у=F(х) принимают одинаковые значения, — корнями или решениями этого уравнения.

Итак, уравнение f(x) =F(х) выражает задачу об отыскании таких значений переменного х, при которых функции f(x) и F(x) имеют оди­наковые значения. Решить уравнение — это значит найти все такие значения х, т. е. все корни (решения) уравнения.

Областью допустимых значений для уравнения (1) называют множество всех х у при которых определены обе функции у=f(х) и у=F(х). Например, для уравнения

область допустимых значений определяется условиями:

Область допустимых значений может заранее ограничиваться некоторыми условиями. Например, могут иметь смысл лишь поло­жительные или лишь целые корни. В этом случае надо рассмат­ривать уравнение лишь для положительных (или целых) значе­ний х.

Тогда мы считаем, что функции f(x) и F(х) заданы на некотором множестве X, и рассматриваем уравнение лишь на этом множестве.

Пусть даны два уравнения

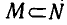
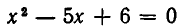
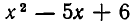
Обозначим множество корней уравнения (1) через M, а множество корней уравнения (2) через N. Если (то есть, если всякий ко­рень уравнения (1) является корнем уравнения (2)), то уравнение (2) называют следствием уравнения (1). Например, уравнение является следствием уравнения 2х—6= 0. В самом деле, корнем уравнения 2х — 6=0 является х=3, а при этом значении многочлен обращается в нуль.

Если множества М и N корней уравнений (1) и (2) совпадают, то эти уравнения называются равносильными. Иными словами, уравнения

равносильны, если всякий корень уравнения (2) является корнем уравнения (3) и, обратно, всякий корень уравнения (3) является корнем уравнения (2).

В частности, уравнения равносильны, если множества М и N — пусты, то есть если каждое из уравнений не имеет решений.

Если уравнения (2) и (3) равносильны, то каждое из них явля­ется следствием другого.

Следует отметить, что понятие равносильности уравнений существенно зависит от того, какие значения корней считаются до­пустимыми. Рассмотрим, например, уравнения:

Корнями первого уравнения является число х=3, а второго — числа 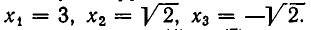Так как эти множества различны, то уравнения (4) и (5) не являются равносильными. Но если рассматривать лишь рациональные значения корней уравнения, то уравнения (4) и (5) оказываются равносильными — ибо они имеют по единственному рациональному корню х = 3. Как правило, мы будем в дальнейшем рассматривать равносильность относительно множества всех действительных чисел. Иными словами, уравнения будут считаться равносильными, если они имеют одни и те же действительные корни.

Совокупности уравнений

Пусть задано несколько уравнений

и требуется найти все значения х, которые удовлетворяют хотя бы одному из этих уравнений. Тогда говорят, что задана совокупность уравнений, а такие значения х называют решениями или корнями этой совокупности. Следует различать совокупность уравнений и систему уравнений — для системы уравнений требуется искать значения неизвестных, которые удовлетворяют всем урав­нениям, а для совокупности — хотя бы одному из уравнений.

Чтобы отличать совокупность уравнений от системы уравнений, мы будем обозначать совокупность квадратными скобками, а систему — фигурными скобками.

имеет одно решение 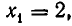, а совокупность тех же уравнений

имеет три решения

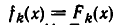
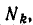
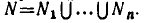
Обозначим множество решений уравнения через а мно­жество решений совокупности уравнений (1) через N. Тогда Например, множество решений совокупности

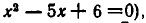
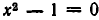
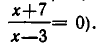
состоит из чисел 2, 3 (решений уравнения 1, —1 (решений уравнения ) и —7 (решения уравнения Число х=3 является решением, хотя при этом значении не определена функция

Две совокупности уравнений

называются равносильными, если они имеют одно и то же множество корней.

Например, совокупности уравнений

равносильны — их корнями являются числа 2, —2 и —3.

Преобразования уравнений

При решении уравнений мы переходим от одного уравнения к другому, пока не придем к уравне­нию вида х = а или совокупности уравнений такого вида. Возьмем, например, уравнение

Прибавляя к обеим частям этого уравнения (—Зх+3) и приводя подобные члены, получаем уравнение

А теперь умножим обе части уравнения (2) на и получим, что

В процессе решения этого уравнения мы прибавляли к обеим частям уравнения некоторое алгебраическое выражение (а именно, —Зх+3), умножали обе части уравнения на одно и то же число (а именно, на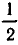). Кроме того, мы выполняли тождественные преоб­разования. Заметим, что уравнения (1), (2) и (3) имели одно и толь­ко одно решение х = 2. Таким образом, все проведенные преобра­зования приводили к уравнениям, равносильным первоначальному уравнению (1), имевшим с ним одно и то же решение.

Однако не всегда одинаковые преобразования обеих частей уравнения приводят к уравнению, равносильному первоначальному. Рассмотрим уравнение:

Его решением является х = 3. Если же мы умножим обе части уравнения на х — 2, то получим уравнение:

Это уравнение, кроме решения х=3, имеет еще решение х= 2— оно имеет лишний корень по сравнению с (4).

С другой стороны, если мы возьмем уравнение (5), имеющее решения х=2, х=3, и «сократим» его на х — 2 (то есть разделим обе части уравнения на х — 2), то получим уравнение 2х+1= =х+4 с единственным решением х=3. Значит, здесь мы в про­цессе решения потеряли корень х=2.

Не является «безобидным» и прибавление к обеим частям уравнения одного и того же алгебраического выражения. Например, уравнение

имеет решение х =2. Но если прибавить к обеим частям этого уравнения выражение 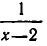, то получим уравнение

для которого х =2 не является решением — обе части этого уравнения не имеют смысла при х=2. Таким образом, произошла по­теря решения.

Эти примеры наглядно показывают, что при преобразовании уравнений необходима осторожносгь — неправильно преобразуя уравнение, мы можем как приобрести лишние решения, так и поте­рять решения данного уравнения. При этом надо иметь в виду, что приобретение лишних решений не столь опасно, как потеря сущест­вующих. Ведь после того, как уравнение решено, можно подставить все найденные решения в заданное уравнение и отобрать те из реше­ний, которые ему удовлетворяют. А потерянные решения восстано­вить уже нельзя.

Из изложенного видно, что, прежде чем решать конкретные ви­ды уравнений, надо познакомиться с общей теорией уравнений, выяснить, какие преобразования приводят к равносильным уравне­ниям, какие дают посторонние решения, а при каких решения мо­гут быть потеряны. Только после этого мы сможем решать урав­нения «с открытыми глазами».

Теоремы о равносильности уравнений

Сформулируем сна­чала условия, при которых одно уравнение является следствием другого уравнения. Потом из этих условий будут получены условия равносильности уравнений.

Теорема:

Если к обеим частям уравнения

прибавить функцию 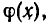имеющую смысл при всех допустимых значениях неизвестного х, то получится новое уравнение

являющееся следствием данного.

Доказательство:

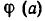
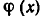
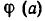
В самом деле, пусть а—корень уравнения (1). Тогда f(а)=F(а). Но является некоторым числом, так как по условию функция определена для всех допустимых значений х и, в частности, при х=а. Прибавим к обеим частям числового равенства f(a)=F(а) число . Получим равенство

которое показывает, что число а является корнем уравнения (2). Таким обра­зом, всякий корень уравнения (1) является корнем уравнения (2), то есть уравнение (2) является следствием уравнения (1).

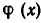
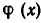
Условие, что функция определена при всех допустимых значениях х, существенно. Если не определено при х=а, где а — решение уравния (1), то уравнение (2) не является следствием уравнения (1) и уравнения (1) и (2) неравносильны: х = а является решением для (1), но не является ре­шением для уравнения (2). Примером могут служить уравнения (6) и (7) из п. 5.

Прибавление к обеим частям уравнения одного и того же выражения не может привести к приобретению посторонних корней, если это прибавление не сопровождается приведением подобных членов или иными преобразованиями, меняющими область определения уравнения (например, сокращением дробей). Рассмотрим, например, уравнение

Если прибавить к обеим частям — 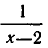и привести подобные члены, то получим уравнение Зх +1= 9 — х, имеющее решение х = 2. Это решение не принадлежит области определения исходного уравнения и потому не удовлетворяет ему.

Перейдем к вопросу об умножении обеих частей уравнения на одно и то же выражение.

Теорема:

Если обе части уравнения

умножить на функцию 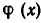, имеющую смысл при всех допустимых значениях х, то получится новое уравнение

являющееся следствием уравнения (3).

Доказательство.

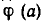
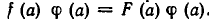
Пусть а — корень уравнения (3). Тогда справедливо равенство f(а)=F(а). Умножим обе части этого равенства на число . Мы получим числовое равенство Оно показывает, что а является корнем и уравнения (4). Таким образом, всякий корень уравнения (3) является корнем уравнения (4), то есть (4) — следст­вие (3).

Из доказанных теорем следует, например, что уравнение

является следствием уравнения

Действительно, уравнение (5) получается из уравнения (6) прибавлением к обеим частям функции Зх+2 и умножением полученного уравнения на х + 2.

Многочлены определены при всех значениях х. Поэтому прибавление к обеим частям уравнения многочлена, равно как и умножение обеих частей

уравнения на многочлен, приводит к уравнению, являющемуся следствием исходного.

Оговорка о том, что 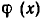должно иметь смысл при всех допустимых зна­чениях х, существенна для справедливости теоремы 2. Рассмотрим, напри­мер, уравнение

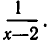
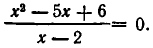
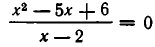
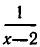
и умножим обе части этого уравнения на Мы получим уравнение Оно уже не является следствием исходного: уравнение (7) имеет корни 2 и 3, а уравнение — лишь корень 3. При­чиной потери корня явилось то, что функция не определена при х = 2, а это значение как раз является корнем заданного уравнения.

Докажем теперь теоремы о равносильности уравнений. Чтобы доказать равносильность двух уравнений, надо показать, что пер­ вое из них является следствием второго, а второе — следствием первого.

Теорема:

Если функция 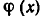определена при всех допустимых значениях неизвестного х, то уравнения

Доказательство:

Мы уже видели, что при условии теоремы уравнение (9) является следствием уравнения (8). Но уравнение (8) в свою очередь получается из уравнения (9) прибавлением к обеим частям функции — 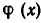и приведением подобных членов.

Так как функция 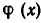определена при всех допустимых значениях х, то уравнение (8) является следствием уравнения (9). Тем самым доказано, что уравнения (8) и (9) равносильны.

Из доказанной теоремы вытекает правило перенесения слагае­мых из одной части уравнения в другую: если некоторое слагаемое данного уравнения перенести из одной части в другую, изменив знак этого слагаемого на противоположный, то получится уравнение, равносильное данному.

В самом деле, в силу теоремы 3 уравнения

равносильны: уравнение (11) получается путем прибавления функции — 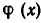к обеим частям уравнения (10) и приведения подобных членов.

Кратко правило перенесения слагаемых формулируют так: всякое слагаемое можно перенести из одной части уравнения в другую, изменив при этом его знак на противоположный.

Из доказанной теоремы вытекает, что всякое уравнение f(х) =F(х) можно заменить равносильным ему уравнением вида Ф(х) = 0. Для этого достаточно перенести F(х) в левую часть уравнения, заменив знак на противоположный, и положить f(х)— F(х) =Ф (х).

Теорема:

Если функция 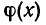определена для всех допустимых значений х и ни при одном допустимом значении х не обращается в нуль, то уравнения

Доказательство:

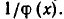
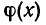
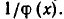
Мы уже видели (теорема 2), что уравнение (13) является следствием уравнения (12). Докажем, что уравнение (12) в свою очередь является следствием уравнения (13). Уравнение (12) получается из уравнения (13) умножением обеих частей на функцию Так как по условию функция определена для всех допустимых значений х и не обращается при этих значениях в нуль, то функция также опре­делена при всех допустимых значениях х. Поэтому уравнение (12) является следствием уравнения (13), а значит, эти уравнения равносильны.

Из доказанной теоремы вытекает, например, что уравнения

равносильны в области действительных чисел. В самом деле, урав­нение (15) получается из уравнения (14) умножением на функцию 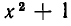, а эта функция всюду определена и не обращается в нуль при действительных значениях х.

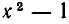
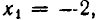
не являются равносильными — второе получается из первого умножением на функцию , а эта функция обращается в нуль при х = ± 1. Поэтому второе уравнение, кроме корня удовлетворяющего и первому уравнению, имеет еще и корни

Уравнения (12) и (13) могут быть неравносильными и в том случае, когда множитель 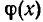теряет смысл при некоторых допустимых значениях неизвестного. Например, уравнения

неравносильны: множитель 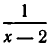теряет смысл при х = 2, а x = 2 как раз является корнем уравнения

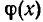
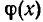
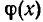
Если в ходе решения уравнения приходилось умножать обе части этого уравнения на выражение , содержащее неизвестное, то надо проверить две вещи: а) Не обращается ли в нуль при допустимых значениях не­ известного? б) Не теряет ли смысл при некоторых допустимых значениях неизвестного?

В первом случае среди найденных корней могут оказаться посторонние корни, и надо проверить все найденные корни, удов­летворяют ли они первоначально заданному уравнению. Во вто­ром же случае возможна потеря корней, и мы должны подставить в заданное уравнение значения неизвестного, при которых теряет смысл 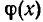— среди этих значений могут оказаться потерянные в ходе решения корни уравнения.

Из теоремы 4 непосредственно вытекает справедливость утверждения: если обе части уравнения умножить на произвольное отлич­ное от нуля число, то получим уравнение, равносильное данному.

Это утверждение кратко формулируют так: обе части уравнения можно умножать на произвольное отличное от нуля число.

Видео:Алгебра 10 класс (Урок№12 - Решение алгебраических уравнений разложением на множители.)Скачать

Уравнения с одним неизвестным

Алгебраические уравнения с одним неизвестным:

Рациональным алгебраическим уравнением с одним неизвестным называют уравнение вида

где R(х) — алгебраическая дробь относительно х. К такому виду можно в силу теорем 3 и 5, привести любое уравнение 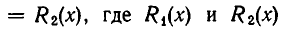— алгебраические дроби. Например, уравнение

является рациональным алгебраическим. В дальнейшем мы будем называть такие уравнения просто алгебраическими.

Применяя теоремы о равносильности уравнений, можно заменить каждое уравнение вида (1) равносильным ему уравнением вида:

где f(x)— многочлен от х. Для этого надо записать дробь R(x) в ви­де отношения двух многочленов. Мы получим уравнение:

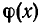
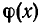
где f(х) и — многочлены от х. Но дробь может равняться нулю лишь в случае, когда равен нулю ее числитель. Поэтому решение уравнения (1) сводится к решению уравнения f(x)=0, где f(х) — многочлен от х. При этом нужно иметь в виду, что решениями уравнения (1) являются лишь те корни уравнения (2), при которых дробь R(x) имеет смысл (то есть отлично от нуля).

Пример:

Перенесем 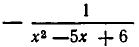в левую часть уравнения и приведем получившуюся сумму к общему знаменателю. Получим уравнение:

Приравнивая нулю числитель этой дроби, получаем уравнение х—2=0, корнем которого является число х=2. Однако при x=2 дробь 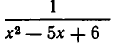не определена. Поэтому заданное уравне­ние корней не имеет.

Метод разложения на множители

Рассмотрим некоторые методы решения алгебраических уравнений, а также отдельные виды таких уравнений.

Выше было сказано, что при решении уравнения его заменяют другими уравнениями или совокупностями уравнений, равносильными заданному, но более простыми

Рассмотрим следующий пример. Пусть надо решить уравнение:

Мы знаем, что произведение может равняться нулю тогда и только тогда, когда хоть один из его сомножителей равен нулю. Поэтому, чтобы решить уравнение (1), надо найти все значения, при кототых хоть один из сомножителей равен нулю. А это все равно, что решить совокупность уравнений

Решая ее, находим для х значения 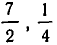и 6. Они и дают корни уравнения (1).

Метод, примененный для решения уравнения (1), в общем виде формулируется так.

Теорема:

Если функции определены на некотором множестве М, то на этом множестве уравнение

равносильно совокупности уравнений

Доказательство:

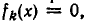
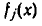
Пусть а — одно из решений совокупности (3). Это означает, что а является корнем одного из уравнений этой совокуп­ности, например, уравнения а все остальные функции опреде­лены при х = а. Но тогда

так как один из сомножителей 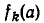равен нулю. Следовательно, любое решение совокупности (3) является корнем уравнения (2).

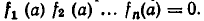
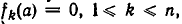
Наоборот, пусть а — корень уравнения (2). Тогда f (а)=0, то есть Но произведение равно нулю лишь в случае, когда хоть один из сомножителей равен нулю. Поэтому хотя бы одно из чисел равно нулю. Это означает, что а является корнем хотя бы одного из уравнений то есть одним из решений совокупно­сти уравнений (3).

Пример:

Левая часть этого уравнения разлагается на множители следующим образом:

Отсюда следует, что уравнение (4) равносильно совокупности уравнений:

Решая уравнения этой совокупности, получаем корни урав­нения (4):

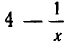
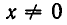
не равносильны, так как при х = 0 функция не определена. На множестве же они равносильны.

В некоторых случаях разложение на множители связано с искусственными преобразованиями. Рассмотрим, например, уравне­ние:

Нетрудно заметить, что

Поэтому уравнение (б) можно записать в виде:

Таким образом, все свелось к решению совокупности двух квадратных уравнений:

Решая их, находим корни уравнения (6):

Метод введения нового неизвестного

Наряду с методом разложения на множители часто применяется другой метод — введе­ние нового неизвестного.

Рассмотрим следующий пример:

Если раскрыть скобки, то получится уравнение четвертой степени, решить которое довольно сложно. Мы поступим иначе. Обозначим 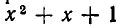через r. Тогда

Поэтому уравнение (1) после введения нового неизвестного z принимает вид

Решая это квадратное уравнение, получаем, что его корни равны:

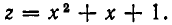
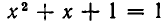
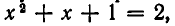
Но Поэтому х удовлетворяет или уравнению или уравнению то есть совокупности уравнений:

Решая ее, получаем:

Метод, примененный для решения уравнения (1), в общем виде заключается в следующем.

Пусть дано уравнение F(х)=0 и пусть функцию F(х) можно представить в виде 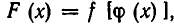так что уравнение F (х)=0 записывается в виде

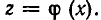
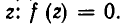
Введем новое неизвестное z, положив Тогда вместо уравнения (1) получаем уравнение относительно Дока­жем следующую теорему.

Теорема:

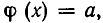
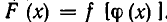
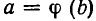
Если а — один из корней уравнения f(z) = 0, а b — один из корней уравнения то b является одним из корней уравнения F(х)=0, где . Обратно, если b — корень уравнения F(х)=0, то — один из корней уравнения f(z)= 0 .

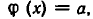
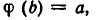
Доказательство. Пусть b — корень уравнения где а — корень уравнения f (z)=0; f(а) =0. Тогда и потому

Таким образом, b удовлетворяет уравнению F (х) = 0.

Обратно, пусть b — корень уравнения F(х)=0 и 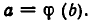Тогда

Следовательно, а — корень уравнения f(z)=0. Теорема доказана.

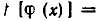
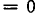
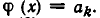
Из доказанной теоремы следует, что решение уравнения вида сводится к следующему: сначала находят корни уравнения f(z) =0; после этого надо решить все уравнения Совокупность корней этих уравнений и дает решение уравнения (2).

Биквадратные уравнения

Метод замены неизвестного при­ меняется для решения уравнений вида

Такие уравнения называют биквадратными. Чтобы решить уравнение (1), положим 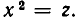Тогда получим квадратное уравнение:

Его корнями являются числа:

Поэтому корни уравнения (1) получаются путем решения уравнений 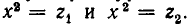Значит, мы получаем четыре корня для уравнения (1)

Четыре корня возникают при различных комбинациях знаков:

При решении биквадратных уравнений (как и при решении квадратных уравнений) иногда приходится извлекать квадратные корни из отрицательных чисел. Это приводит к так называемым комплексным числам, которые будут изучены в главе V.

Пример. Решить уравнение

Полагая 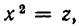получаем квадратное уравнение:

Его корнями являются числа 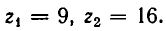Значит, корни урав­нения (8) имеют вид:

Возвратные уравнения 3-й и 4-й степеней

Многочлен n-й степени

называется возвратным, если его коэффициенты, одинаково уда­ ленные от начала и от конца, равны между собой. Иными словами, коэффициенты возвратного многочлена n-й степени удовлетворяют условию

Алгебраическое уравнение вида f(х)=0, где f(х) — возврат­ный многочлен, называют возвратным уравнением. Примерами та­ких уравнений являются:

Рассмотрим решение возвратных уравнений третьей и четвер­той степеней. Возвратное уравнение третьей степени имеет вид:

Группируя члены, разложим выражение в левой части уравнения на множители:

Отсюда видно, что одним из корней уравнения (1) является х=—1 . Два других корня получаются путем решения квадратного уравнения

Пример:

Разлагая левую часть уравнения на множители, получаем:

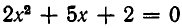
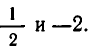
Корни квадратного уравнения равны Поэтому корнями заданного уравнения являются числа

Приведем пример задачи, сводящейся к разобранному типу уравнений.

Задача:

Из квадратного листа жести со стороной а см вы­резают по углам четыре квадратика со стороной х см и делают из получившейся фигуры коробку. При каком значении х объем коробки равен ?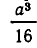

Решение:

Основанием коробки является квадрат со сторо­ной а-2x, а ее высота равна х. Значит, объем коробки равен 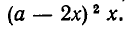По условию имеем уравнение:

Положим 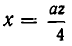. Мы получим для z уравнение

Разлагая на множители, получаем

Поэтому корни нашего уравнения равны

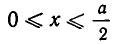
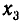
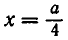
Из условия задачи следует, что Поэтому не удовлетворяет условию. Итак, либо , либо

Теперь рассмотрим возвратное уравнение 4-й степени:

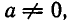
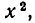
Так как то х=0 не является корнем этого уравнения. Поэтому если разделить обе части уравнения (2) на то получим равносильное уравнение:

Введем новое неизвестное z, положив 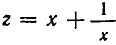. Так как

Следовательно, уравнение (3) превращается в квадратное уравнение отно­сительно z

Решив это уравнение, найдем его корни 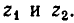Чтобы найти х, остается решить совокупность уравнений:

Она сводится к совокупности квадратных уравнений:

Пример. Решить уравнение

Перепишем это уравнение в виде

и введем новое неизвестное 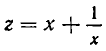. Получим уравнение:

Решая его, находим: 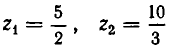. Чтобы найти корни уравнения (4), надо решить уравнения:

Из них получаем:

Наряду с уравнениями вида (1) и (2) рассматривают так называемые кососимметричные уравнения, или, иначе, возвратные уравнения второго рода. При n=4 они имеют вид:

Это уравнение сводится к

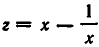
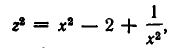
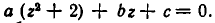
После этого вводят новое неизвестное по формуле . Так как то уравнение (6) сводится к квадратному уравнению Дальнейшее решение ведется так же, как и для обычных возвратных уравнений.

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:Способы решения алгебраических уравненийСкачать

Методы решения уравнений — обзор

В этой статье дан краткий обзор всех основных методов решения уравнений. Здесь также приведены ссылки на материалы с подробной информацией по каждому методу. Это дает возможность познакомиться со всеми методами решения уравнений, а в случае необходимости — изучить методы решения уравнений углубленно.

Видео:Алгебра 11 класс (Урок№49 - Уравнения. Методы решения уравнений.)Скачать

Метод введения новой переменной (замены переменной)

Метод введения новой переменной, он же метод замены переменной, позволяет решать уравнения f(g(x))=0 или f₁(g(x))=f₂(g(x)) , где f , f₁ и f₂ – некоторые функции, а x – неизвестная переменная, а также уравнения, которые могут быть приведены к указанному виду. Состоит метод во введении новой переменной t=g(x) . Введение переменной позволяет от исходного уравнения f(g(x))=0 или f₁(g(x))=f₂(g(x)) перейти к уравнению с новой переменной f(t)=0 или f₁(t)=f₂(t) соответственно. Дальше находятся корни полученного уравнения с новой переменной: t₁, t₂, …, t_n . После этого осуществляется возврат к старой переменной, для чего составляется совокупность уравнений g(x)=t₁, g(x)=t₂, …, g(x)=t_n . Решение этой совокупности дает интересующее нас решение исходного уравнения.

Например, метод введения новой переменной позволяет решить уравнение . Здесь стоит принять . Это позволяет перейти от исходного уравнения к квадратному уравнению t 2 −3·t+2=0 с новой переменной t , которое имеет два корня t₁=1 и t₂=2 . Обратная замена происходит путем составления совокупности двух уравнений и . Это рациональные уравнения. Решением первого является x=2 , а решением второго является x=1,5 . Так методом введения новой переменной получено решение исходного уравнения: 1,5 , 2 .

Подробное описание метода введения новой переменной, включающее обоснование метода, алгоритм решения уравнений этим методом и примеры решения характерных уравнений, дано в этой статье.

Видео:Решение систем уравнений второго порядка. 8 класс.Скачать

Метод разложения на множители

Метод разложения на множители предназначен для решения уравнений f₁(x)·f₂(x)·…·f_n(x)=0 , где f₁(x), f₂(x),…, f_n(x) – некоторые выражения, x – переменная. То есть, методом разложения на множители решаются уравнения, в левой части которых находится произведение нескольких выражений, а в правой – нуль. Суть метода состоит в замене решения уравнения f₁(x)·f₂(x)·…·f_n(x)=0 решением совокупности уравнений f₁(x)=0, f₂(x)=0, …, f_n(x)=0 на области допустимых значений (ОДЗ) для исходного уравнения.

Приведем простой пример. Уравнение может быть решено методом разложения на множители. Переходим от исходного уравнения к совокупности двух уравнений и . Иррациональное уравнение имеет единственное решение x₁=1 . Логарифмическое уравнение тоже имеет единственное решение x₂=4 . Значит, совокупность уравнений имеет два решения x₁=1 , x₂=4 . Но области допустимых значений для исходного уравнения, которой является множество (3, +∞) , принадлежит лишь одно из решений x₁=1 , x₂=4 , а именно, x₂=4 . Оно и является единственным корнем уравнения .

Подробное описание этого метода и решения других характерных примеров смотрите в статье «метод разложения на множители».

Видео:Решение системы уравнений методом Крамера.Скачать

Метод решения уравнений «дробь равна нулю»

Из названия понятно, что этот метод используется при решении уравнений f(x)/g(x)=0 . Например, он позволяет решить уравнение . Метод состоит в переходе от решения уравнения f(x)/g(x)=0 к решению уравнения f(x)=0 на ОДЗ для исходного уравнения. Следовательно, чтобы решить уравнение , надо решить уравнение (x−1)·(x 2 −4)=0 на ОДЗ для исходного уравнения.

Обоснование метода и примеры с решениями смотрите здесь.

Видео:Решение матричных уравненийСкачать

Метод решения уравнений через преобразования

Метод базируется на преобразовании уравнений с целью выстраивания последовательностей равносильных уравнений и уравнений-следствий со сравнительно простыми последними уравнениями, по решениям которых находятся решения исходных уравнений.

Например, для решения уравнения 3·x 4 −48=0 последовательно проводятся два преобразования: переносится слагаемое −48 из левой части уравнения в правую с противоположным знаком, после чего проводится деление обеих частей уравнения на число 3 . В результате получается равносильное уравнение x 4 =16 , причем очень простое в плане решения. Оно имеет два корня x₁=−2 и x₂=2 . Они и составляют решение исходного уравнения.

Вот другой пример. Замена выражения в левой части уравнения тождественно равным выражением (x−1)·(x+2) дает уравнение-следствие (x−1)·(x+2)=0 , имеющее два корня x₁=1 и x₂=−2 . Проверка показывает, что только первый корень является корнем исходного уравнения, а второй корень – посторонний.

Какие преобразования используются при решении уравнений? Когда нужно делать проверку для отсеивания посторонних корней, а когда такую проверку делать необязательно? Ответы на эти и многие другие вопросы по теме есть в этом материале.

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Метод решения уравнений, сводящихся к числовым равенствам

Иногда в результате преобразования уравнений получаются числовые равенства. Например, уравнение сводится к верному числовому равенству 0=0 , а уравнение сводится к неверному числовому равенству 0=5 . Решением уравнений, сводящихся к верным числовым равенствам, является множество, совпадающее с ОДЗ для исходного уравнения. Так, решением уравнения является множество x≥0 . А уравнения, сводящиеся к неверным числовым равенствам, не имеют решений. То есть, уравнение не имеет решений.

Здесь есть один нюанс. Если среди преобразований, приводящих уравнение к верному числовому равенству, есть возведение обеих частей уравнения в одну и ту же четную степень, то нельзя утверждать, что решением уравнения является любое число из ОДЗ. Этот нюанс разобран в статье «решение уравнений, сводящихся к числовым равенствам».

Видео:Решение систем линейных алгебраических уравнений методом Крамера.Скачать

Функционально-графический метод

Обзор методов решения уравнений продолжаем функционально-графическии методом. Этот метод предполагает использование функций, отвечающих частям решаемого уравнения, а точнее, их графиков и свойств. Можно выделить три основных направления функционально-графического метода:

• Графический метод
• Метод, базирующийся на возрастании-убывании функций
• Метод оценки

Давайте рассмотрим их.

Графический метод

Первое направление базируется на использовании графиков функций. Это так называемый графический метод решения уравнений. По этому методу, во-первых, выполняется построение в одной прямоугольной системе координат графиков функций, отвечающих частям уравнения. Во-вторых, по чертежу определяется количество точек пересечения графиков, сколько точек пересечения – столько и корней у решаемого уравнения. В-третьих, определяются абсциссы точек пересечения – это значения корней.

Например, графически можно решить уравнение . Из чертежа, приведенного ниже, видно, что графики имеют единственную точку пересечения с абсциссой 2 . Это единственный корень уравнения.

Метод, базирующийся на возрастании-убывании функций

Второе направление в своей основе имеет использование свойств возрастающих и убывающих функций. Соответствующий метод используется тогда, когда есть возможность подобрать корень уравнения и доказать возрастание функции, отвечающей одной из частей уравнения, и убывание функции, отвечающей другой части уравнения. В этом случае подобранный корень является единственным.
Приведем пример. Для уравнения 3 (1−x) 3 +1=2 x несложно подобрать корень, им является число 1 . Также несложно обосновать убывание функции, соответствующей левой части уравнения, и возрастание функции, отвечающей правой части уравнения. Это доказывает единственность подобранного корня.

За более полной информацией следуйте сюда

Метод оценки

Третье направление основано на использовании свойств ограниченности функций. Это так называемый метод оценки. Согласно этому методу, в первую очередь нужно оценить значения выражений, находящихся в левой и правой части уравнения. Если множества, соответствующие полученным оценкам, не пересекаются, то уравнение не имеет корней. Если множества имеют конечное число общих элементов t₁ , t₂ , …, t_n , то решение уравнения f(x)=g(x) заменяется решением совокупности систем , , …, . Если же множества, соответствующие оценкам имеют бесконечно много общих элементов, то надо либо уточнять оценки, либо искать другой метод решения.

Например, методом оценки можно решить уравнение . Значения левой части этого уравнения не превосходят нуля, а значения правой части не меньше нуля. Это позволяет перейти к системе , решение которой дает искомое решение уравнения.

Видео:Матричный метод решения систем уравненийСкачать

Метод освобождения от внешней функции

Метод освобождения от внешней функции используется для решения уравнений h(f(x))=h(g(x)) , где f , g и h – функции, причем функция y=h(t) принимает каждое свое значение по одному разу, в частности, строго возрастает или строго убывает, а x – независимая переменная. Этот метод состоит в переходе от уравнения h(f(x))=h(g(x)) к уравнению f(x)=g(x) на ОДЗ для исходного уравнения.

Например, методом освобождения от внешней функции можно решить уравнение . Здесь в качестве внешней функции выступает y=h(t) , где . Эта функция возрастающая как сумма двух возрастающих функций и , значит, каждое свое значение она принимает по одному разу. Это позволяет перейти от исходного уравнения к уравнению . Равносильные преобразования позволяют привести последнее уравнение к квадратному уравнению x 2 +x−2=0 , которое имеет два корня x₁=−2 и x₂=1 . Из этих корней только x₁=−2 принадлежит ОДЗ для исходного уравнения. Следовательно, x₁=−2 – единственный корень исходного уравнения.

Рекомендуем детально разобраться с этим методом решения уравнений, обратившись к материалу статьи «метод освобождения от внешней функции».

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Метод решения уравнений через ОДЗ

Через ОДЗ решаются уравнения, области допустимых значений которых являются либо пустыми множествами, либо состоят из конечного количества чисел. Когда ОДЗ есть пустое множество, уравнение не имеет решений. Когда ОДЗ состоит из конечного количества чисел, то следует по очереди проверить эти числа через подстановку. Те из них, которые удовлетворяют решаемому уравнению являются его корнями, остальные – не являются.

Например, уравнение не имеет решений, так как ОДЗ для него есть пустое множество. А для уравнения ОДЗ состоит из двух чисел −1 и 7 . Проверка подстановкой показывает, что −1 является корнем уравнения, а 7 – не является.

Более полная информация по этому методу решения уравнений содержится в этой статье.

Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Метод возведения обеих частей уравнения в одну и ту же степень

Этот метод, в основном, используется для решения иррациональных уравнений. Он заключается в возведении обеих частей уравнения в одну и ту же степень с целью избавления от корней. Например, возведение обеих частей уравнения в квадрат дает уравнение без корня 1−5·x=(x−3) 2 . Возведение в нечетную степень дает равносильное уравнение. Возведение в четную степень в общем случае дает уравнение-следствие, поэтому, при этом необходимо позаботиться об отсеивании посторонних корней. Причем отсеивание следует проводить способом, не связанным с ОДЗ, обычно, через проверку подстановкой, так как возведение частей уравнения в четную степень может приводить к появлению посторонних корней в рамках ОДЗ.

Аналогично разбираемый метод может использоваться и для решения уравнений, в которых фигурируют степени с рациональными и иррациональными показателями. Решения соответствующих примеров смотрите здесь.

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Метод решения уравнений по определению логарифма

По определению логарифма, как правило, решают уравнения следующего вида log_h(x)f(x)=g(x) , например, log₂(x 2 +4·x+3)=3 , log₂(9−2 x )=3−x , log_x(3·x lgx +4)=2·lgx и т.п.

Согласно методу решения уравнений по определению логарифма, решение уравнения log_h(x)f(x)=g(x) заменяется решением уравнения f(x)=(h(x)) g(x) на ОДЗ переменной x для исходного уравнения. Например, от уравнения log_x(3·x lgx +4)=2·lgx можно перейти к уравнению 3·x lgx +4=x 2·lgx на ОДЗ для исходного уравнения.

Более полная информация содержится в основной статье.

Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать

Метод потенцирования

Методом потенцирования решаются логарифмические уравнения, обе части которых являются логарифмами по одному и тому же основанию, например, lgx=lg(3·x+5) , и т.п. Метод заключается в замене решения уравнения log_h(x)f(x)=log_h(x)g(x) решением уравнения f(x)=g(x) на ОДЗ для исходного уравнения. По этому методу от уравнения lgx=lg(3·x+5) следует перейти к уравнению x=3·x+5 на ОДЗ для исходного уравнения, которая определяется двумя условиями: x>0 , 3·x+5>0 .

Обоснование метода и примеры с подробными решениями смотрите в этой статье.

Метод логарифмирования

Метод подразумевает логарифмирование обеих частей уравнения по одному и тому же основанию. К нему следует прибегать тогда, когда логарифмирование позволяет избавиться от степеней с переменной в показателях. В частности, его можно использовать для решения показательных уравнений, обе части которых являются степенями с одинаковыми основаниями, например, 5 1−x =5 2·x+1 . Почленное логарифмирование этого уравнения дает очень простое уравнение 1−x=2·x+1 , решение которого дает решение исходного уравнения.

Также метод подходит для решения показательных уравнений, степени в которых имеют разные основания и отличающиеся показатели, например, . Более того, метод логарифмирования является чуть ли не основным методом решения показательно-степенных уравнений, вроде таких x lgx−1 =100 , .

Более детальная информация и примеры с решениями есть в этом материале.