- 1. Прямые и плоскости в пространстве R n
- 1.1. Расстояние от точки до прямой
- 1.2. Нормированное уравнение прямой
- 2. Общее уравнение плоскости в R 3
- 2.1. Угол между двумя плоскостями
- 2.2. Уравнение плоскости, проходящей через три различные точки, не лежащие на одной прямой
- 2.3. Нормированное уравнение плоскости. Отклонение точки от плоскости
- 3. Прямая линия R 3
- 4. Выпуклые множества точек на плоскости. Неравенства
- 4.1. Неравенства
- 4.2. Выпуклые множества точек на плоскости
- 5. Выпуклые множества в пространстве. Неравенства
- 5.1. Нестрогие линейные неравенства
- Общее уравнение прямой: описание, примеры, решение задач
- Общее уравнение прямой: основные сведения
- Неполное уравнение общей прямой
- Общее уравнение прямой, проходящей через заданную точку плоскости
- Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
- Составление общего уравнения прямой
- Уравнение прямой
- Уравнение прямой на плоскости
- Уравнение прямой с угловым коэффициентом
- Уравнение прямой в отрезках на осях
- Уравнение прямой, проходящей через две различные точки на плоскости
- Параметрическое уравнение прямой на плоскости
- Каноническое уравнение прямой на плоскости
- Уравнение прямой в пространстве
- Уравнение прямой, проходящей через две различные точки в пространстве
- Параметрическое уравнение прямой в пространстве
- Каноническое уравнение прямой в пространстве
- Прямая как линия пересечения двух плоскостей
- 🌟 Видео
Видео:Видеоурок "Общее уравнение прямой"Скачать

1. Прямые и плоскости в пространстве R n
Изучим пространство R n с другой точки зрения. Будем рассматривать его элементы не как векторы, а как точки, то есть А(х1, х2, . хn), где хi — координаты точки А ( i = 1, 2, . n). О(0. 0) — назовем началом координат.
Элементы R, R 2 , R 3 можно интерпретировать как координаты точек соответственно на прямой, на плоскости, в пространстве; поэтому R принято называть числовой прямой, R 2 — числовой плоскостью, R 3 — числовым пространством.
Как мы уже знаем, при n>3 непосредственное обращение к геометрии невозможно, но многие факты, относящиеся к R n , носят общий характер, не зависящий от n. Так свойства решений линейных уравнений и методы их исследования не зависят от числа переменных. Тогда можно сказать, что в этом смысле пространство R n обладает геометрическими свойствами, подобными свойствам пространств R, R 2 , R 3 . Множества точек в R 4 (“фигуры”) будем задавать с помощью уравнений, неравенств с n переменными и их систем как области их решений.
Определение 1. Область решений совместной системы линейных уравнений с n переменными ранга r назовем k-мерной плоскостью в R n , где k = n — r (k — число свободных, а r — базисных переменных.)
Отметим два случая:
1. r = n, k = 0. Система имеет единственное решение, которое представляет собой точку в R n , то есть точку можно считать нуль-мерной плоскостью.
2. r = 0, k = n. Все уравнения являются тождествами (0 = 0), все переменные свободные, область решений системы совпадает со всем пространством R n , то есть само пространство можно считать n-мерной плоскостью.
Если этих два крайних случая исключить из рассмотрения, то очевидно, что k может меняться в пределах 1 £ k £ n — 1.
Определение 2. Плоскость наибольшей возможной в R n размерности, но не совпадающей со всем пространством, то есть (n-1)-мерную плоскость, называют гиперплоскостью, а плоскость наименьшей возможной размерности, но не являющуюся точкой, то есть одномерную плоскость, называют прямой.
R — само одномерно и в нем не может быть плоскостей меньшей размерности.
R 2 — (числовая плоскость) — в нем гиперплоскость совпадает с прямой — это одномерная плоскость.
R 3 — (числовое пространство) — здесь гиперплоскостью является двухмерная плоскость, а прямой — одномерная плоскость; других плоскостей нет.
З а м е ч а н и е. При n > 3 кроме гиперплоскостей и прямой существуют плоскости промежуточных размерностей (n-2)-мерные, . трехмерные, двухмерные.
Гиперплоскость обычно задают одним линейным уравнением
в котором не все коэффициенты равны нулю, то есть

Условие (1.2) равносильно тому, что ранг системы, состоящей из одного уравнения (1.1), равен 1.
Пусть теперь система состоит из двух уравнений

Если ее матрица А имеет ранг 1, то
В этом случае гиперплоскости, определенные уравнениями системы (1.3), называются параллельными и, если

(то есть ранг расширенной матрицы равен 2), то система несовместна:
гиперплоскости, определенные уравнениями системы (1.3), не имеют общих точек (не пересекаются); если же

(то есть ранг расширенной матрицы равен 1), то система сводится к одному уравнению, две гиперплоскости совпадают.
И наконец, если ранг матрицы А равен 2, то система определяет (n-2)-мерную плоскость.
Прямую можно задать совместной системой линейных уравнений с n переменными ранга r = n-1. Если известны две точки А(а1,а2. аn), B(b1,b2. bn) прямой, то эту систему можно записать в виде

где X(x1, x2, . xn) — текущая переменная точка прямой.
Систему уравнений (1.4) называют уравнениями прямой, проходящей через две точки А и В.
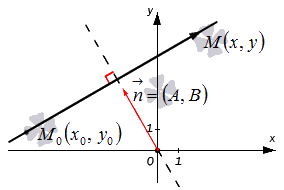
1.1. Расстояние от точки до прямой
Рассмотрим прямую l в R 2 , заданную уравнением
А × х + В × у + С = 0
и точку М(х1,у1) вне данной прямой.
Обозначим через d расстояние MN (MN перпендикуляр к l). Уравнение перпендикуляра можно записать в виде В × (х — х1) — А × (у — у1) = 0.


то есть t — коэффициент пропорциональности. Поэтому из (1.5) следует, что

C другой стороны, точка N(x2,y2) принадлежит l, следовательно, из (1.5) получаем
Подставим эти значения в уравнение прямой А × х + В × у + С = 0. Получим
А × х2 + В × у2 + С = А × (х1 + А × t) + В × ( y1 + В × t) + С = (А × х1 + В × у1 + C) + t × (А 2 + В 2 ) = 0


З а м е ч а н и е. (следствие).

является расстоянием от прямой до начала координат.
2. Разделив обе части общего уравнения прямой на 

свободный член которого 
1.2. Нормированное уравнение прямой
Пусть дана прямая l. Проведем через начало координат прямую n, перпендикулярную l. Пусть Р — точка пересечения прямых. Возьмем единичный вектор 
Выразим уравнение l через два параметра:

Пусть М(х,у) принадлежит l. Тогда проекция 








Следовательно, точка М принадлежит прямой l означает, что координаты этой точки удовлетворяют уравнению

Это и есть нормированное уравнение прямой l.
Пусть теперь имеем общее уравнение прямой l:
l: А × х + В × у + С = 0
l:
t × A = Cos q , t × B = Sin q , t × C = -p.
t 2 × A 2 + t 2 × В 2 = Cos 2 q + Sin 2 q = 1
t 2 × (A 2 + В 2 ) = 1 (1.9)

Следовательно, чтобы получить из общего уравнения прямой
А × х + В × у + С = 0
нормированное уравнение (1.8) следует умножить его на нормирующий множитель (1.9), знак которого противоположен С.
Видео:Видеоурок "Общие уравнения прямой"Скачать

2. Общее уравнение плоскости в R 3
Зафиксируем произвольную декартову прямоугольную систему координат Oxyz и рассмотрим произвольное уравнение первой степени
А × х + В × у + С × z + D = 0, (2.1)
где A, B, C, D — произвольные константы, хотя бы одна из которых не равна 0.
Уравнение (2.1) заведомо имеет хотя бы одно решение (x0, y0, z0).
Действительно, пусть С ¹ 0, следовательно, взяв произвольные (x0, y0), мы получим 
которое эквивалентно (2.1).
Рассмотрим разность между (2.1) и (2.2).
которое эквивалентно (2.1).
Докажем, что уравнение (2.2) и, стало быть, уравнение (2.1), определяет плоскость (П) в Oxyz.

то есть хотя бы одна координата его не равна 0.
Возьмем произвольную точку М0(x, y, z), принадлежащую плоскости П, то есть ее координаты удовлетворяют уравнению (2.3), ибо в этом случае вектор 


Если точка М(x,y,z) не принадлежит плоскости П, то ее координаты не удовлетворяют (2.3), ибо в этом случае вектор 

Таким образом, мы доказали следующее утверждение.
Теорема 2.1. Если в R 3 фиксирована произвольная декартова система координат Oxyz (прямоугольная), то всякое уравнение первой степени с тремя переменными x,y,z определяет относительно этой системы плоскость.
З а м е ч а н и я.
1. Уравнение (2.1) с произвольными коэффициентами А, В, С (хотя бы один из которых не должен быть равен нулю) называется общим уравнением плоскости в R 3 .
2. Если два общих уравнения
А × х + В × у + С × z + D = 0
определяют одну и ту же плоскость, следовательно, существует число t, такое, что справедливы равенства
Рассмотреть(самостоятельно) неполные уравнения плоскости, когда
1) А = 0; 2) В = 0; 3) C = 0; 4) D = 0;
5) A = В = 0; 6) A = C = 0; 7) B = C = 0;
8) A = В = C = 0; 9) A = C = D = 0; 10) В = C = D = 0;
2.1. Угол между двумя плоскостями
Пусть даны две плоскости П1 и П2, которые заданы уравнениями
Чтобы определить угол между плоскостями, достаточно определить угол j между их нормальными векторами 

По определению скалярного произведения

Условие параллельности двух плоскостей заключается в пропорциональности координат векторов 


Условие “плоскость П1 перпендикулярна к плоскости П2” определяет, что Cos j = 0
2.2. Уравнение плоскости, проходящей через три различные точки, не лежащие на одной прямой
Пусть даны три точки М1(x1,y1,z1), М2(x2,y2,z2) и М3(x3,y3,z3). Необходимо вывести уравнение плоскости, проходящей через эти три точки. Так как эти три точки не лежат на одной прямой, то векторы 




Теорема 2.2. Для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы выполнялось следующее условие

Из условия (2.8) получим уравнение первой степени относительно x,y,z. Оно и является уравнением искомой плоскости.
2.3. Нормированное уравнение плоскости. Отклонение точки от плоскости
Пусть дана плоскость П. Проведем через начало координат прямую n перпендикуляр к плоскости П, и пусть Р — точка пересечения прямой n и плоскости П.
Рассмотрим вектор 






прn 

Так как 

Определение 2.1. Назовем отклонением d точки М от плоскости П число +d в случае, когда точка М и начало координат точка О лежат по разные стороны от плоскости П, и число -d — в случае, когда точка М и начало координат точка О лежат по одну сторону от плоскости П, (куда направлен вектор 
Для нахождения отклонения d точки М0(x0,y0,z0) от плоскости П следует в левую часть нормированного уравнения плоскости П поставить на место х,у,z координаты x0,y0,z0 точки М.
А × х + В × у + С × z + D = 0
определяют одну ту же плоскость, то существует t такое, что
t × A = Cos a , t × B = Sin b , t × C = Sin g , t × D = -p.
Так как сумма квадратов направляющих косинусов равна 1, то
t 2 × (A 2 + B 2 + C 2 )=1,

где знак t противоположен знаку коэффициента D.
Для приведения общего уравнения плоскости
А × х + В × у + С × z + D = 0
к нормированному виду (2.9) следует умножить его на нормирующий множитель (2.10), знак которого противоположен знаку коэффициента D.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

3. Прямая линия R 3
Прямую в пространстве R 3 можно задать как пересечение двух плоскостей, определяемых уравнениями

Приведем (3.1) к каноническому виду.
Для этого достаточно найти:
1) хотя бы одну точку М1(x1,y1,z1), через которую проходит прямая
Так как плоскости, определяемые (3.1), не параллельны и не сливаются, то нарушается (2.6), то есть хотя бы одна из пропорций

а это значит, что хотя бы один из определителей второго порядка


отличен от нуля.

Тогда, взяв вместо z произвольное число z1 и подставив его в уравнение (3.1), можно определить соответственно x1 и y1

Можно взять z1=0. Тогда, воспользовавшись (3.2), получим, что прямая проходит через точку 
Пусть текущая точка М(x,y,z). Тогда уравнение линии можно записать в виде


Уравнение прямой, проходящей через данную точку М1(x1,y1,z1) и перпендикулярной плоскости А × х + В × у + С × z + D = 0, имеет вид

Уравнение прямой, параллельной данной плоскости и проходящей через данную точку М0(x0,y0,z0).
Пусть плоскость П задана уравнением
Тогда уравнение прямой имеет вид
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

4. Выпуклые множества точек на плоскости. Неравенства
4.1. Неравенства
Пусть задана линия
то есть это множество точек, координаты которых удовлетворяют этому уравнению. Аналогично можно рассмотреть множество точек, координаты которых удовлетворяют неравенству

Это уравнение определяет окружность с центром в точке С(a,b) радиуса r, (Рис. 8.4);
(х — a) 2 + (х — b) 2 — r 2 0
определяет множество точек, лежащих внутри круга с центром в точке С(a,b) радиуса r, (Рис. 8.5);
(х — a) 2 + (х — b) 2 — r 2 > 0
определяет множество точек, лежащих вне этого круга с центром в точке С(a,b) радиуса r (Рис. 8.6);
Множество точек, удовлетворяющих (4.1), называют областью решений этого уравнения.
Аналогично будем говорить об области решений неравенств (4.2) и (4.3).
Пусть теперь F(x, y) — линейное уравнение, то есть имеет вид
F(x, y) = A × x + B × y + C, (4.4)
где A, B, C — константы .
Любое невырожденное уравнение A × x + B × y + C = 0 определяет линию L в R 2 , рассмотрим
A × x + B × y + C 0 (4.5)
A × x + B × y + C > 0, (4.6)
По отношению к прямой линии все точки разбились на два множества Ф1 и Ф2, лежащие по разные стороны от прямой L (Рис 8.7).
Покажем, что эти множества определяются неравенствами (4.5) и (4.6).
Так как эти точки не лежат на прямой, то имеем
Действительно, так как точки М1(х1,у1), М2(х2,у2) лежат по разные стороны от прямой (4.4), то существует точка М0(х0,у0) такая, что она делит отрезок М1М2 в отношении 


Так как точка М0(х0,у0) принадлежит прямой L, то имеем
Подставим (4.7) в (4.4):

то есть d 1+ l × d 2 = 0, откуда d 1 = -l × d 2 , но l > 0, следовательно, d 1 и d 2 имеют разные знаки.
Пусть, например, d 1 0, d 2 > 0, тогда точка М1(х1,у1) удовлетворяет неравенству (4.5), а точка М2(х2,у2) — неравенству (4.6).
Множество точек, лежащих на некоторой прямой и по одну сторону от нее, называют полуплоскостью.
Очевидно, что каждая прямая L разбивает плоскость П на две полуплоскости, для которых она является общей границей. Считается, что граница принадлежит сразу двум полуплоскостям.
Если (4.4) — это граница, то нестрогие неравенства
A × x + B × y + C £ 0
A × x + B × y + C ³ 0
Пусть задана система неравенств

Геометрически система (4.8) может быть истолкована как область решений этой системы, то есть это множество точек , которые одновременно удовлетворяют всем неравенствам этой системы, то есть 

З а м е ч а н и е. В частности может иметь место 
Областью решений системы линейных неравенств

является очевидно пересечение полуплоскостей, определяемых каждым из неравенств.
Эту область будем называть многоугольником.
Не исключены также случаи вырождения многоугольной области в прямую или луч, а многоугольника — в отрезок или точку.
4.2. Выпуклые множества точек на плоскости
Определение 4.1. Множество точек называется выпуклым, если вместе с двумя его точками М1 и М2 ему принадлежат и все внутренние точки отрезка М1М2.
Выпуклые множества: полуплоскость, круг, отрезок и так далее.
Многоугольники могут быть как выпуклые, так и невыпуклые. Геометрически это можно всегда увидеть, но этот факт также может быть
установлен и аналитически.
Теорема 4.1. Пусть дана полуплоскость
Ф1: A × x + B × y + C 0
Если А × х0 + В × у0 + С 0, то тогда полуплоскость будет выпуклой.
Д о к а з а т е л ь с т в о :
Координаты точки М1 можно выразить через координаты точек М1 и М2:


Подставим эти выражения в неравенство полуплоскости

l > 0, 
а по определению 8.4 такое множество называется выпуклым.
З а м е ч а н и е. Определение выпуклого множества сформулировано в предположении, что в этом множестве имеются по крайней мере две точки. Если множество пустое (в этом случае его обозначают как Æ ) или состоит из одной точки, то его тоже считают выпуклым.
Для выпуклых множеств имеет место следующая теорема:
Теорема 4.2. Пересечение любого числа выпуклых множеств — выпуклое множество.
Д о к а з а т е л ь с т в о :
Пусть j 1, j 2, . j n — выпуклые множества и их пересечение 

Пусть имеем две произвольные точки М1(х1,у1) и М2(х2,у2), принадлежащие пересечению множеств j i, тогда, так как все множества j i выпуклы, то им принадлежит и отрезок М1М2, а следовательно, 

Следствие. Область решений системы линейных неравенств (), если она не представляет собой Æ , является выпуклой многоугольной областью или выпуклым многоугольником.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

5. Выпуклые множества в пространстве. Неравенства
По аналогии с пространством R 2 можно рассмотреть геометрию и неравенства в пространстве R 3 .
определяют множество точек пространства, координаты которых удовлетворяют этим неравенствам.
(х — a) 2 + (х — b) 2 + (z — c) 2 2
определяет внутреннюю область шара, ограниченную сферой
(х — a) 2 + (х — b) 2 + (z — c) 2 = r 2
с центром в точке С(а,b,c) и радиусом r, а неравенство
(х — a) 2 + (х — b) 2 + (z — c) 2 > r 2
определяет множество точек, находящихся вне этого шара.
Множество точек, лежащих в некоторой плоскости и по одну сторону от нее, называют полупространством.
5.1. Нестрогие линейные неравенства
D + A × x + B × y + C × z и
D + A × x + B × y + C × z > 0
определяют два полупространства, общей границей которых будет плоскость
D + A × x + B × y + C × z = 0.
Доказательство этого факта проводится так же, как и в случае двух переменных.
Пусть дана система линейных неравенств с тремя неизвестными

Областью решений системы (5.3) является пересечение полупространств, то есть такое множество точек, если оно не пусто, которое является решением каждого из неравенств системы. Это пересечение полупространств называют многогранной областью или (в случае ограниченности) многогранником.
З а м е ч а н и е.
1. Понятие выпуклого множества точек и теорема о выпуклости пересечения выпуклых множеств точек сохраняет силу и для пространства.
(Провести доказательство самостоятельно).
2. Так как полупространство выпукло, то область решений системы линейных неравенств (5.3), если она не пуста, является выпуклой многогранной областью (или выпуклым многогранником), если она ограничена.
Не исключены случаи вырождения.

Видео:11. Прямая в пространстве и ее уравненияСкачать

Общее уравнение прямой: описание, примеры, решение задач
Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой. Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и как осуществлять переходы от общего уравнения к другим типам уравнений прямой. Всю теорию закрепим иллюстрациями и решением практических задач.
Видео:9 класс, 7 урок, Уравнение прямойСкачать

Общее уравнение прямой: основные сведения
Пусть на плоскости задана прямоугольная система координат O x y .
Любое уравнение первой степени, имеющее вид A x + B y + C = 0 , где А , В , С – некоторые действительные числа ( А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид A x + B y + C = 0 при некотором наборе значений А , В , С .
указанная теорема состоит из двух пунктов, докажем каждый из них.
- Докажем, что уравнение A x + B y + C = 0 определяет на плоскости прямую.
Пусть существует некоторая точка М 0 ( x 0 , y 0 ) , координаты которой отвечают уравнению A x + B y + C = 0 . Таким образом: A x 0 + B y 0 + C = 0 . Вычтем из левой и правой частей уравнений A x + B y + C = 0 левую и правую части уравнения A x 0 + B y 0 + C = 0 , получим новое уравнение, имеющее вид A ( x — x 0 ) + B ( y — y 0 ) = 0 . Оно эквивалентно A x + B y + C = 0 .
Полученное уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 является необходимым и достаточным условием перпендикулярности векторов n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) . Таким образом, множество точек M ( x , y ) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n → = ( A , B ) . Можем предположить, что это не так, но тогда бы векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) не являлись бы перпендикулярными, и равенство A ( x — x 0 ) + B ( y — y 0 ) = 0 не было бы верным.
Следовательно, уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение A x + B y + C = 0 определяет ту же прямую. Так мы доказали первую часть теоремы.
- Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени A x + B y + C = 0 .
Зададим в прямоугольной системе координат на плоскости прямую a ; точку M 0 ( x 0 , y 0 ) , через которую проходит эта прямая, а также нормальный вектор этой прямой n → = ( A , B ) .
Пусть также существует некоторая точка M ( x , y ) – плавающая точка прямой. В таком случае, векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:
n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) = 0
Перепишем уравнение A x + B y — A x 0 — B y 0 = 0 , определим C : C = — A x 0 — B y 0 и в конечном результате получим уравнение A x + B y + C = 0 .
Так, мы доказали и вторую часть теоремы, и доказали всю теорему в целом.
Уравнение, имеющее вид A x + B y + C = 0 – это общее уравнение прямой на плоскости в прямоугольной системе координат O x y .
Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.
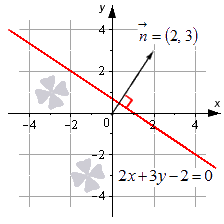
Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой A x + B y + C = 0 .
Рассмотрим конкретный пример общего уравнения прямой.
Пусть задано уравнение 2 x + 3 y — 2 = 0 , которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n → = ( 2 , 3 ) . Изобразим заданную прямую линию на чертеже.
Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2 x + 3 y — 2 = 0 , поскольку координаты всех точек заданной прямой отвечают этому уравнению.
Мы можем получить уравнение λ · A x + λ · B y + λ · C = 0 , умножив обе части общего уравнения прямой на число λ , не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.
Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

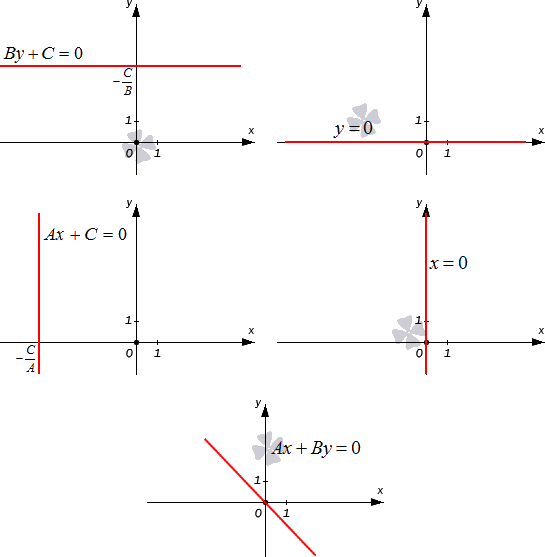
Неполное уравнение общей прямой
Полное общее уравнение прямой – такое общее уравнение прямой A x + B y + C = 0 , в котором числа А , В , С отличны от нуля. В ином случае уравнение является неполным.
Разберем все вариации неполного общего уравнения прямой.
- Когда А = 0 , В ≠ 0 , С ≠ 0 , общее уравнение принимает вид B y + C = 0 . Такое неполное общее уравнение задает в прямоугольной системе координат O x y прямую, которая параллельна оси O x , поскольку при любом действительном значении x переменная y примет значение — C B . Иначе говоря, общее уравнение прямой A x + B y + C = 0 , когда А = 0 , В ≠ 0 , задает геометрическое место точек ( x , y ) , координаты которых равны одному и тому же числу — C B .
- Если А = 0 , В ≠ 0 , С = 0 , общее уравнение принимает вид y = 0 . Такое неполное уравнение определяет ось абсцисс O x .
- Когда А ≠ 0 , В = 0 , С ≠ 0 , получаем неполное общее уравнение A x + С = 0 , задающее прямую, параллельную оси ординат.
- Пусть А ≠ 0 , В = 0 , С = 0 , тогда неполное общее уравнение примет вид x = 0 , и это есть уравнение координатной прямой O y .
- Наконец, при А ≠ 0 , В ≠ 0 , С = 0 , неполное общее уравнение принимает вид A x + B y = 0 . И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел ( 0 , 0 ) отвечает равенству A x + B y = 0 , поскольку А · 0 + В · 0 = 0 .
Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.
Известно, что заданная прямая параллельна оси ординат и проходит через точку 2 7 , — 11 . Необходимо записать общее уравнение заданной прямой.
Решение
Прямая, параллельная оси ординат, задается уравнением вида A x + C = 0 , в котором А ≠ 0 . Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения A x + C = 0 , т.е. верно равенство:
Из него возможно определить C , если придать A какое-то ненулевое значение, к примеру, A = 7 . В таком случае получим: 7 · 2 7 + C = 0 ⇔ C = — 2 . Нам известны оба коэффициента A и C , подставим их в уравнение A x + C = 0 и получим требуемое уравнение прямой: 7 x — 2 = 0
Ответ: 7 x — 2 = 0
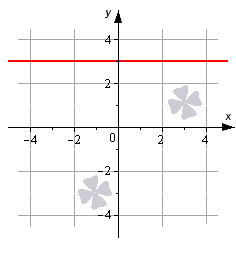
На чертеже изображена прямая, необходимо записать ее уравнение.
Решение
Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси O x и проходит через точку ( 0 , 3 ) .
Прямую, которая параллельна очи абсцисс, определяет неполное общее уравнение B y + С = 0 . Найдем значения B и C . Координаты точки ( 0 , 3 ) , поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой B y + С = 0 , тогда справедливым является равенство: В · 3 + С = 0 . Зададим для В какое-то значение, отличное от нуля. Допустим, В = 1 , в таком случае из равенства В · 3 + С = 0 можем найти С : С = — 3 . Используем известные значения В и С , получаем требуемое уравнение прямой: y — 3 = 0 .
Ответ: y — 3 = 0 .
Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Общее уравнение прямой, проходящей через заданную точку плоскости
Пусть заданная прямая проходит через точку М 0 ( x 0 , y 0 ) , тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: A x 0 + B y 0 + C = 0 . Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A ( x — x 0 ) + B ( y — y 0 ) + C = 0 , это уравнение эквивалентно исходному общему, проходит через точку М 0 ( x 0 , y 0 ) и имеет нормальный вектор n → = ( A , B ) .
Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.
Даны точка М 0 ( — 3 , 4 ) , через которую проходит прямая, и нормальный вектор этой прямой n → = ( 1 , — 2 ) . Необходимо записать уравнение заданной прямой.
Решение
Исходные условия позволяют нам получить необходимые данные для составления уравнения: А = 1 , В = — 2 , x 0 = — 3 , y 0 = 4 . Тогда:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 1 · ( x — ( — 3 ) ) — 2 · y ( y — 4 ) = 0 ⇔ ⇔ x — 2 y + 22 = 0
Задачу можно было решить иначе. Общее уравнение прямой имеет вид A x + B y + C = 0 . Заданный нормальный вектор позволяет получить значения коэффициентов A и B , тогда:
A x + B y + C = 0 ⇔ 1 · x — 2 · y + C = 0 ⇔ x — 2 · y + C = 0
Теперь найдем значение С, используя заданную условием задачи точку М 0 ( — 3 , 4 ) , через которую проходит прямая. Координаты этой точки отвечают уравнению x — 2 · y + C = 0 , т.е. — 3 — 2 · 4 + С = 0 . Отсюда С = 11 . Требуемое уравнение прямой принимает вид: x — 2 · y + 11 = 0 .
Ответ: x — 2 · y + 11 = 0 .
Задана прямая 2 3 x — y — 1 2 = 0 и точка М 0 , лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна — 3 . Необходимо определить ординату заданной точки.
Решение
Зададим обозначение координат точки М 0 как x 0 и y 0 . В исходных данных указано, что x 0 = — 3 . Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство:
2 3 x 0 — y 0 — 1 2 = 0
Определяем y 0 : 2 3 · ( — 3 ) — y 0 — 1 2 = 0 ⇔ — 5 2 — y 0 = 0 ⇔ y 0 = — 5 2
Ответ: — 5 2
Видео:Написать канонические и параметрические уравнения прямой в пространствеСкачать

Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.
Для начала рассмотрим переход от общего уравнения вида A x + B y + C = 0 к каноническому уравнению x — x 1 a x = y — y 1 a y .
Если А ≠ 0 , тогда переносим слагаемое B y в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: A x + C A = — B y .
Это равенство возможно записать как пропорцию: x + C A — B = y A .
В случае, если В ≠ 0 , оставляем в левой части общегь уравнения только слагаемое A x , прочие переносим в правую часть, получаем: A x = — B y — C . Выносим – В за скобки, тогда: A x = — B y + C B .
Перепишем равенство в виде пропорции: x — B = y + C B A .
Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.
Задано общее уравнение прямой 3 y — 4 = 0 . Необходимо преобразовать его в каноническое уравнение.
Решение
Запишем исходное уравнение как 3 y — 4 = 0 . Далее действуем по алгоритму: в левой части остаётся слагаемое 0 x ; а в правой части выносим — 3 за скобки; получаем: 0 x = — 3 y — 4 3 .
Запишем полученное равенство как пропорцию: x — 3 = y — 4 3 0 . Так, мы получили уравнение канонического вида.
Ответ: x — 3 = y — 4 3 0 .
Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.
Прямая задана уравнением 2 x — 5 y — 1 = 0 . Запишите параметрические уравнения этой прямой.
Решение
Осуществим переход от общего уравнения к каноническому:
2 x — 5 y — 1 = 0 ⇔ 2 x = 5 y + 1 ⇔ 2 x = 5 y + 1 5 ⇔ x 5 = y + 1 5 2
Теперь примем обе части полученного канонического уравнения равными λ , тогда:
x 5 = λ y + 1 5 2 = λ ⇔ x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R
Ответ: x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R
Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y = k · x + b , но только тогда, когда В ≠ 0 . Для перехода в левой части оставляем слагаемое B y , остальные переносятся в правую. Получим: B y = — A x — C . Разделим обе части полученного равенство на B , отличное от нуля: y = — A B x — C B .
Задано общее уравнение прямой: 2 x + 7 y = 0 . Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.
Решение
Произведем нужные действия по алгоритму:
2 x + 7 y = 0 ⇔ 7 y — 2 x ⇔ y = — 2 7 x
Ответ: y = — 2 7 x .
Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида x a + y b = 1 . Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на – С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y :
A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1
Необходимо преобразовать общее уравнение прямой x — 7 y + 1 2 = 0 в уравнение прямой в отрезках.
Решение
Перенесем 1 2 в правую часть: x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 .
Разделим на -1/2 обе части равенства: x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 .
Преобразуем далее в необходимый вид: 1 — 1 2 x — 7 — 1 2 y = 1 ⇔ x — 1 2 + y 1 14 = 1 .
Ответ: x — 1 2 + y 1 14 = 1 .
В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.
Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:
x a + y b ⇔ 1 a x + 1 b y — 1 = 0 ⇔ A x + B y + C = 0 y = k x + b ⇔ y — k x — b = 0 ⇔ A x + B y + C = 0
Каноническое уравнение преобразуется к общему по следующей схеме:
x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x ( y — y 1 ) ⇔ ⇔ a y x — a x y — a y x 1 + a x y 1 = 0 ⇔ A x + B y + C = 0
Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ A x + B y + C = 0
Заданы параметрические уравнения прямой x = — 1 + 2 · λ y = 4 . Необходимо записать общее уравнение этой прямой.
Решение
Осуществим переход от параметрических уравнений к каноническому:
x = — 1 + 2 · λ y = 4 ⇔ x = — 1 + 2 · λ y = 4 + 0 · λ ⇔ λ = x + 1 2 λ = y — 4 0 ⇔ x + 1 2 = y — 4 0
Перейдем от канонического к общему:
x + 1 2 = y — 4 0 ⇔ 0 · ( x + 1 ) = 2 ( y — 4 ) ⇔ y — 4 = 0
Ответ: y — 4 = 0
Задано уравнение прямой в отрезках x 3 + y 1 2 = 1 . Необходимо осуществить переход к общему виду уравнения.
Решение:
Просто перепишем уравнение в необходимом виде:
x 3 + y 1 2 = 1 ⇔ 1 3 x + 2 y — 1 = 0
Ответ: 1 3 x + 2 y — 1 = 0 .
Видео:Каноническое уравнение прямой в пространстве Преход от общего уравненияСкачать

Составление общего уравнения прямой
Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A ( x — x 0 ) + B ( y — y 0 ) = 0 . Там же мы разобрали соответствующий пример.
Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.
Задана прямая, параллельная прямой 2 x — 3 y + 3 3 = 0 . Также известна точка M 0 ( 4 , 1 ) , через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.
Решение
Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n → = ( 2 , — 3 ) : 2 x — 3 y + 3 3 = 0 . Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 2 ( x — 4 ) — 3 ( y — 1 ) = 0 ⇔ 2 x — 3 y — 5 = 0
Ответ: 2 x — 3 y — 5 = 0 .
Заданная прямая проходит через начало координат перпендикулярно прямой x — 2 3 = y + 4 5 . Необходимо составить общее уравнение заданной прямой.
Решение
Нормальный вектором заданной прямой будет направляющий вектор прямой x — 2 3 = y + 4 5 .
Тогда n → = ( 3 , 5 ) . Прямая проходит через начало координат, т.е. через точку О ( 0 , 0 ) . Составим общее уравнение заданной прямой:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 3 ( x — 0 ) + 5 ( y — 0 ) = 0 ⇔ 3 x + 5 y = 0
Видео:УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать

Уравнение прямой
Видео:13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

Уравнение прямой на плоскости
Любую прямую на плоскости можно задать уравнением прямой первой степени вида
где A и B не могут быть одновременно равны нулю.
Уравнение прямой с угловым коэффициентом
Общее уравнение прямой при B≠0 можно привести к виду
где k — угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.
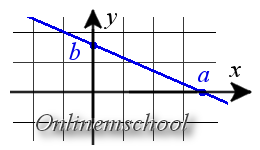
Уравнение прямой в отрезках на осях
Если прямая пересекает оси OX и OY в точках с координатами ( a , 0) и (0, b ), то она может быть найдена используя формулу уравнения прямой в отрезках
| x | + | y | = 1 |
| a | b |
Уравнение прямой, проходящей через две различные точки на плоскости
Если прямая проходит через две точки M( x 1, y 1) и N( x 2, y 2), такие что x 1 ≠ x 2 и y 1 ≠ y 2, то уравнение прямой можно найти, используя следующую формулу
| x — x 1 | = | y — y 1 |
| x 2 — x 1 | y 2 — y 1 |
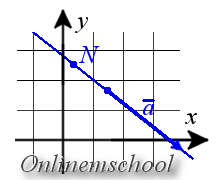
Параметрическое уравнение прямой на плоскости
Параметрические уравнения прямой могут быть записаны следующим образом
x = l t + x 0 y = m t + y 0
где N( x 0, y 0) — координаты точки лежащей на прямой, a = — координаты направляющего вектора прямой.
Каноническое уравнение прямой на плоскости
Если известны координаты точки N( x 0, y 0) лежащей на прямой и направляющего вектора a = ( l и m не равны нулю), то уравнение прямой можно записать в каноническом виде, используя следующую формулу
| x — x 0 | = | y — y 0 |
| l | m |
Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки
x — 1 2 — 1 = y — 7 3 — 7
Упростив это уравнение получим каноническое уравнение прямой
Выразим y через x и получим уравнение прямой с угловым коэффициентом
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
x = t + 1 y = -4 t + 7
Решение. Так как M y — N y = 0, то невозможно записать уравнение прямой проходящей через две точки.
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
Видео:§8.1 Общее уравнение прямой на плоскостиСкачать

Уравнение прямой в пространстве
Уравнение прямой, проходящей через две различные точки в пространстве
Если прямая проходит через две точки M( x 1, y 1, z 1) и N( x 2, y 2, z 2), такие что x 1 ≠ x 2, y 1 ≠ y 2 и z 1 ≠ z 2, то уравнение прямой можно найти используя следующую формулу
| x — x 1 | = | y — y 1 | = | z — z 1 |
| x 2 — x 1 | y 2 — y 1 | z 2 — z 1 |
Параметрическое уравнение прямой в пространстве
Параметрические уравнения прямой могут быть записаны следующим образом
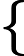 | x = l t + x 0 |
| y = m t + y 0 | |
| z = n t + z 0 |
где ( x 0, y 0, z 0) — координаты точки лежащей на прямой, — координаты направляющего вектора прямой.
Каноническое уравнение прямой в пространстве
Если известны координаты точки M( x 0, y 0, z 0) лежащей на прямой и направляющего вектора n = , то уравнение прямой можно записать в каноническом виде, используя следующую формулу
| x — x 0 | = | y — y 0 | = | z — z 0 |
| l | m | n |
Прямая как линия пересечения двух плоскостей
Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений
🌟 Видео
Видеоурок "Уравнение прямой в отрезках"Скачать

Лекция 23. Виды уравнений прямой на плоскости.Скачать

Видеоурок "Канонические уравнения прямой"Скачать

Уравнение прямой в пространстве. 11 класс.Скачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать