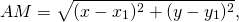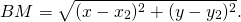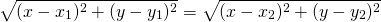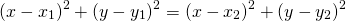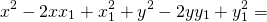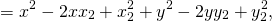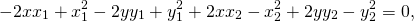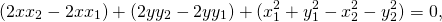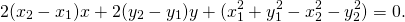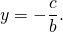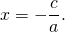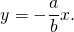Общее уравнение прямой a x b y c 0 становится уравнением оси ординат если (7 видео)

Общее уравнение прямой на плоскости. Неполные уравнения прямой

Общее уравнение прямой: Ax + By + C = 0. Этим уравнением можно задать любую прямую. Коэффициенты А, В, С при этом определяются не однозначно, а с точностью до пропорциональности.

Уравнение Ax + By + C = 0 называется неполным уравнением прямой на плоскости, если хотя бы один из его коэффициентов А, В, С равен нулю.

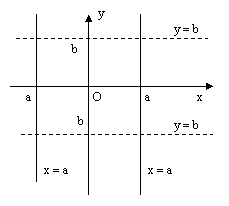
Если коэффициент B = 0, A ≠ 0 ≠ C , то из уравнения Ax + By + C = 0 следует x = — C / A = a. Это уравнение прямой, параллельной оси Оу, отсекающей от оси Ох отрезок величиной а.

Если коэффициент A = 0, B ≠ 0 ≠ C то из уравнения Ax + By + C = 0 следует y = — C / B = b. Это уравнение прямой, параллельной оси Ох, отсекающей от оси Оу отрезок величиной b.

Если C = 0, то уравнение Ax + By + C = 0 принимает вид Ax + By = 0. Ясно, что эта прямая проходит через начало координат.

Если в уравнении Ax + By = 0 коэффициент B ≠ 0 , то отсюда получаем y = — x. Обозначив через

k = — , получаем уравнение, которое носит название уравнения прямой с угловым коэффициентом

Если в уравнении Ax + By = 0 A ≠ B = 0, то Ax = 0 и, сокращая на А, получаем уравнение оси Оу: x = 0.

Если в уравнении Ax + By = 0 B ≠ A = 0, то By = 0 и, сокращая на В, получаем уравнение оси Ох: y = 0.

Подведем итог исследования общего уравнения прямой Ax + By + C = 0:

1) Если A ≠ 0, B ≠ 0, C ≠ 0 , то уравнение Ax + By + C = 0 может быть записано в виде уравнения прямой в отрезках: x /a + y / b = 1 – прямая, отсекающая от осей координат отрезки величиной а и b соответственно.

2) Если A = 0, B ≠ 0, C ≠ 0, то уравнение может быть записано в виде: y = b – прямая параллельная оси Ох и отсекающая от оси Оу отрезок величины b.

3) Если A ≠ 0, B = 0, C ≠ 0, то уравнение может быть записано в виде: x = a – прямая параллельная оси Оу и отсекающая от оси Ох отрезок величины а.

4) Если A = 0, B ≠ 0, C = 0, то уравнение прямой имеет вид: y = 0 – прямая совпадает с осью Ох.

5) Если A ≠ 0, B = 0, C = 0, то уравнение прямой имеет вид: x = 0 – прямая совпадает с осью Оу.

6) Если A ≠ 0, B ≠ 0, C = 0, то уравнение может быть записано в виде: y = k * x – уравнение прямой с угловым коэффициентом.

17. Общее уравнение прямой на плоскости. Уравнение прямой в «отрезках» (с выводом)

Уравнение прямой в отрезках: + = 1.Здесь знаменатели а и b – это координаты точек пересечения прямой с соответствующими координатными осями. С помощью такого уравнения невозможно задать прямую, проходящую через начало координат или параллельную одной из осей.

Пусть ни один из коэффициентов А, В, С общего уравнения прямой Ax + By + C = 0, не равен нулю. Перенесем свободный член С в правую часть уравнения и разделим обе части уравнения на (– С):

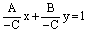
Обозначим . Тогда последнее уравнение можно записать в виде: : + = 1 – это уравнение прямой в отрезках

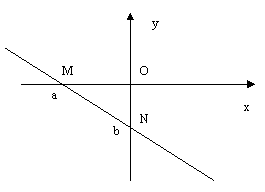
Для построения прямой достаточно взять две точки на этой прямой. Для построения прямой в отрезках удобно найти ее точки пересечения с координатными осями:

М(а, 0) – точка пересечения прямой : + = с осью Ох и

N(0, b) – точка пересечения прямой : + = с осью Оу.

Говорят, что прямая отсекает от координатных осей отрезки ОМ и ОN величина которых равна числам а и b соответственно. Под величиной отрезка ОА здесь понимается не его длина 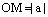, а координата точки М, т.е. число а. Аналогично, величина отрезка ОN равна числу b.

Содержание

Общее уравнение прямой
Общее уравнение прямой a x b y c 0 становится уравнением оси ординат если
Уравнение прямой
🔍 Видео

Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Общее уравнение прямой

В прямоугольной системе координат уравнение прямой имеет вид ax+by+c=0, где a, b и c — некоторые числа (a и b не равны нулю одновременно).

Уравнение вида ax+by+c=0 — общее уравнение прямой.

Пусть в координатной плоскости задана некоторая прямая m.

Построим отрезок AB так, что AB⊥m и AB∩m=F, AF=BF (то есть прямая m — серединный перпендикуляр к AB).

Отметим на прямой m произвольную точку M(x;y).

В прямоугольных треугольниках AFM и BFM:

1) MF — общий катет;

2) AF=BF (по построению).

Значит ΔAFM =ΔBFM (по двум катетам).

Из равенства треугольников следует равенство соответствующих сторон: AM=BM.

Возведём в квадрат обе части равенства:

Уравнение принимает вид: ax+by+c=0.

В силу произвольности выбранной точки M этому уравнению удовлетворяют координаты любой точки прямой m (если же M(x;y)∉m, то AM≠BM и координаты точки M уравнению не удовлетворяют).

Так как точки A и B различны, хотя бы одна из разностей x₂-x₁, y₂-y₁ отлична от нуля, значит a и b не обращаются в нуль одновременно. Отсюда следует, что уравнение прямой в прямоугольной системе координат является уравнением первой степени.

Частные случаи расположения прямой в декартовой системе координат

Подставим эти значения в уравнение прямой: 0·x+by+c=0. Отсюда by+c=0, by=-c,