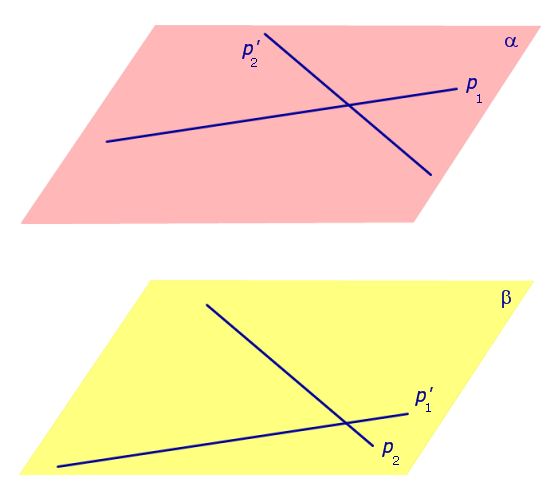
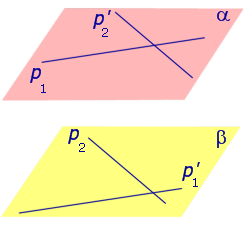
Общее уравнение перпендикуляра к двум прямым (6 видео)

Содержание

Общий перпендикуляр к двум скрещивающимся прямым. Расстояние между скрещивающимися прямыми
Математический портал
Nav view search
Navigation
Search
Расстояние между двумя скрещивающимися прямыми.
Общее уравнение перпендикуляра к двум прямым
🎬 Видео

Видео:Расстояние между скрещивающимися прямыми и уравнение их общего перпендикуляра.Скачать

Общий перпендикуляр к двум скрещивающимся прямым. Расстояние между скрещивающимися прямыми

Теорема. Пусть p₁ и p₂ – две произвольные скрещивающиеся прямые скрещивающиеся прямые . Если рассмотреть всевозможные прямые A₁A₂, такие, что точка A₁ лежит на прямой p₁, а точка A₂ лежит на прямой p₂, то будут выполнены следующие два утверждения:

Среди всех прямых A₁A₂ существует единственная прямая, перпендикулярная к прямой p₁ и к прямой p₂ ( общий перпендикуляр к двум скрещивающимся прямым ).
Среди всех отрезков A₁A₂наименьшую длину имеет отрезок общего перпендикуляра к двум скрещивающимся прямым.

Доказательство. Докажем сначала существование общего перпендикуляра к двум скрещивающимся прямым.

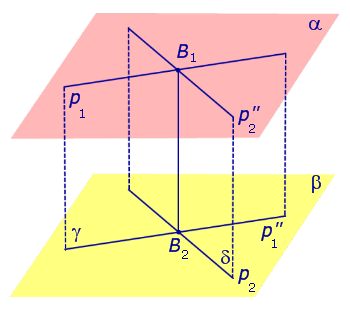
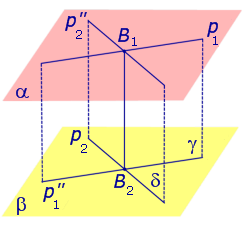
Через произвольную точку прямой p₁ проведем прямую , параллельную прямой параллельную прямой p₂ , а через произвольную точку прямой p₂ проведем прямую , параллельную прямой параллельную прямой p₁ . Обозначим буквой α плоскость, проходящую через прямые p₁ и , а буквой β плоскость, проходящую через прямые p₂ и (рис 1).

Поскольку прямая p₁ параллельна прямой , лежащей на плоскости β , то по признаку параллельности прямой и плоскости прямая p₁ параллельна плоскости β. Точно так же, поскольку прямая параллельна прямой p₂ , лежащей на плоскости β , то прямая по признаку параллельности прямой и плоскости параллельна плоскости β. Таким образом, плоскость α содержит две пересекающиеся прямые p₁ и , паралельные плоскости β. В силу признака параллельности плоскостей заключаем, что плоскости α и β параллельны.

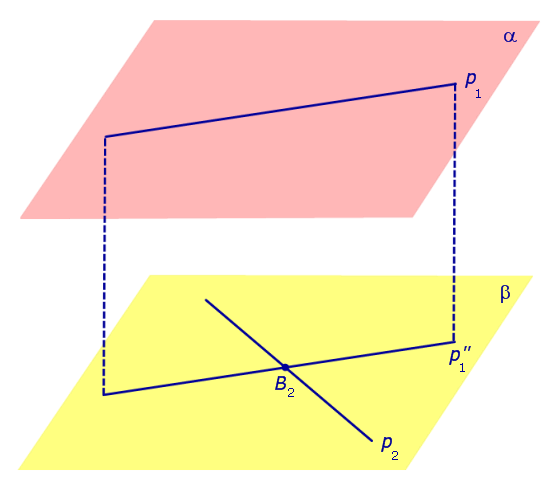
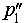
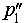
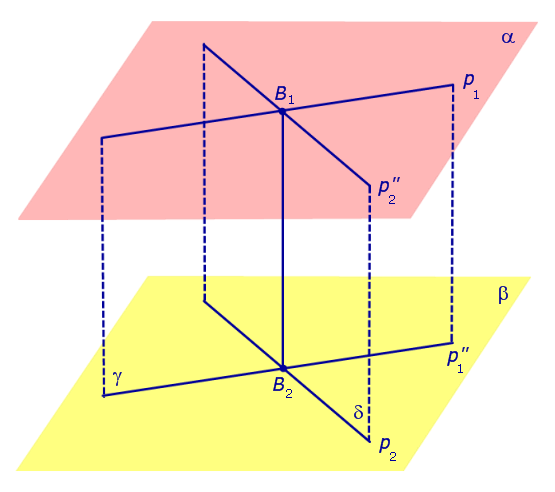
Спроектируем прямую p₁ на плоскость β. Получим прямую , являющуюся проекцией прямой проекцией прямой p₁, и обозначим точку пересечения прямых p₂ и буквой B₂ (рис. 2).

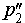
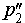
Спроектируем теперь прямую p₂ на плоскость α . Получим прямую , являющуюся проекцией прямой проекцией прямой p₂ , и обозначим точку пересечения прямых p₁ и буквой B₁ (рис. 3).

Доказательство существования общего перпендикуляра к двум скрещивающимся прямым завершено.

Докажем, что построенная прямая B₁B₂ является единственным общим перпендикуляром к прямым p₁ и p₂ .

Таким образом, общий перпендикуляр к прямым p₁ и p₂ является линией пересечения плоскостей γ и δ, то есть прямой B₁B₂ .

Доказательство единственности общего перпендикуляра к двум скрещивающимся прямым завершено. Утверждение 1 доказано.

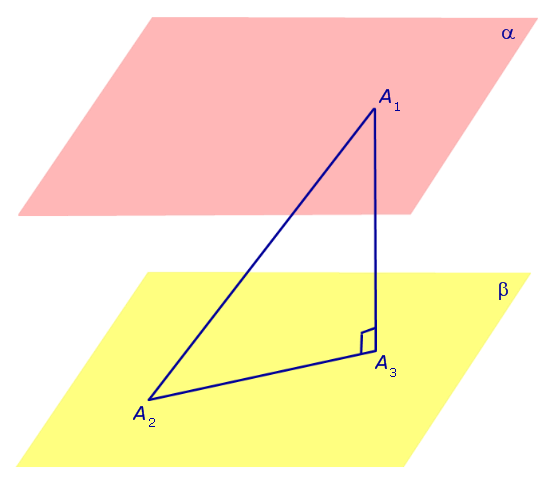
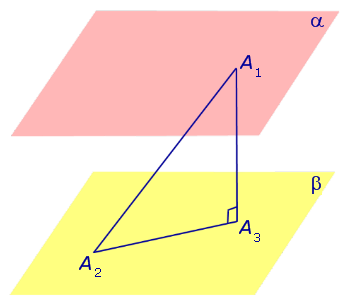
Перейдем к доказательству утверждения 2. Для этого рассмотрим произвольный отрезок A₁A₂ , у которого конец A₁ лежит на плоскости α , а конец A₂ лежит на плоскости β . Опустим перпендикуляр из точки A₁ на плоскость β и обозначим основание этого перпендикуляра символом A₃ (рис. 4).

Если отрезок A₁A₂ не является перпендикуляром к плоскостям α и β, то точка A₃ не совпадет с точкой A₂ , и треугольник A₁A₂A₃ будет прямоугольным треугольником с гипотенузой A₁A₂ и катетом A₁A₃. Поскольку в прямоугольном треугольнике длина катета меньше длины гипотенузы, то

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Математический портал

Видео:Построение общего перпендикуляра к двум скрещивающимся прямым | Стереометрия #33 | ИнфоурокСкачать

Nav view search

Search

Вы здесь:
Home

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Расстояние между двумя скрещивающимися прямыми.

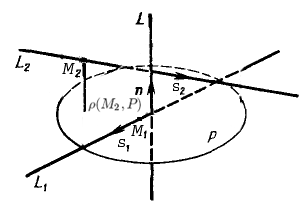
Пусть $L_1: frac=frac=frac$ и $L_2: frac=frac=frac$ — две скрещивающиеся прямые. Расстояние $rho(L_1, L_2)$ между прямыми $L_1$ и $L_2$ можно найти по следующей схеме:

1) Находим уравнение плоскости $P,$ проходящей через прямую $L_1,$ параллельно прямой $L_2:$

Плоскость $P$ проходит через точку $M_1(x_1, y_1, z_1),$ перпендикулярно вектору $overline n=[overline s_1, overline s_2]=(n_x, n_y, n_z),$ где $overline s_1=(m_1, l_1, k_1)$ и $overline s_2=(m_2, l_2, k_2)$ — направляющие вектора прямых $L_1$ и $L_2.$ Следовательно, уравнение плоскости $P: n_x(x-x_1)+n_y(y-y_1)+n_z(z-z_1)=0.$

2) Расстояние между прямыми $L_1$ и $L_2$ равно расстоянию от любой точки прямой $L_2$ до плоскости $P:$

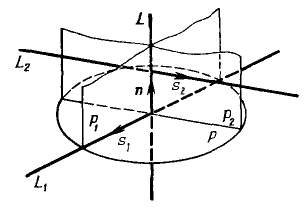
Нахождение общего перпендикуляра скрещивающихся прямых.

Для нахождения общего перпендикуляра прямых $L_1$ и $L_2,$ необходимо найти уравнения
плоскостей $P_1$ и $P_2,$ проходящих, соответственно, через прямые $L_1$ и $L_2,$ перпендикулярно плоскости $P.$

Пусть $P_1: A_1x+B_1y+C_1z+D_1=0;$

Тогда уравнение общего перпендикуляра имеет вид

Пример.

2.214.

а) доказать, что прямые не лежат в одной плоскости, то есть являются скрещивающимися;

б) написать уравнение плоскости, проходящей через прямую $L_2$ параллельно $L_1;$

в) вычислить расстояние между прямыми;

г) написать уравнения общего перпендикуляра к прямым $L_1$ и $L_2.$

Решение.

а) Если прямые $L_1$ и $L_2$ лежат в одной плоскости, то их направляющие вектора $overline(3, 4, -2),$ $overline(6, -4, -1),$ и вектор $overline l,$ соединяющий произвольную точку прямой $L_1$ и произвольную точку прямой $L_2$ компланарны. В качестве такого вектора $overline$ можно выбрать $overline(x_2-x_1, y_2-y_1, z_2-z_1).$ Проверим будут ли эти вектора компланарны.

~~Следовательно, вектора не компланарны и прямые не лежат в одной плоскости.~~

б) Запишем уравнение плоскости, проходящей через прямую $L_2$ параллельно $L_1.$ Эта плоскость проходит через точку $M_2(21, -5, 2)$ перпендикулярно вектору $overline n=[overline s_1, overline s_2].$

~~Таким образом, вектор $overline n$ имеет координаты $overline n(-12, -9, -36).$~~

Находим уравнение плоскости $$P:,, -12(x-21)-9(y+5)-36(z-2)=0Rightarrow$$ $$Rightarrow-12x-9y-36z+252-45+72=0Rightarrow -12x-9y-36z+279=0Rightarrow$$ $$Rightarrow 4x+3y+12z-93=0.$$

~~в) Расстояние между прямыми $L_1$ и $L_2$ равно расстоянию от любой точки прямой $L_1$ до плоскости $P:$~~

~~Ответ: $frac.$~~

г) Найдем уравнения плоскостей $P_1$ и $P_2,$ проходящих, соответственно, через прямые $L_1$ и $L_2,$ перпендикулярно плоскости $P.$

~~Имеем, $M_1=(-7, -4, -3)in P_1,$~~

~~Таким образом, $$P_1: 54(x+7)-44(y+4)-7(z+3)=54x-44y-7z+378-176-21=$$ $$=54x-44y-7z+181=0.$$~~

~~Аналогично находим $P_2:$~~

~~Имеем, $M_2=(21, -5, 2)in P_2,$~~

~~Таким образом, $$P_1: -45(x-21)-76(y+5)+34(z-2)=-45x-76y+34z+945-380-68=$$ $$=-45x-76y+34z+497=0.$$~~

Ответ: $left<begin54x-44y-7z+181=0;\ -45x-76y+34z+497=0.endright. $

~~2.215.~~

~~а) доказать, что прямые не лежат в одной плоскости, то есть являются скрещивающимися;~~

~~б) написать уравнение плоскости, проходящей через прямую $L_2$ параллельно $L_1;$~~

~~в) вычислить расстояние между прямыми;~~

~~г) написать уравнения общего перпендикуляра к прямым $L_1$ и $L_2.$~~

~~Ответ: б) $4x+12y+12z+76=0;$~~

~~г) $left<begin53x-7y-44z-429=0;\ 105x-23y-48z+136=0.endright. $~~

~~Видео:9 класс, 7 урок, Уравнение прямойСкачать~~

Общее уравнение перпендикуляра к двум прямым

~~Признак~~

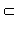
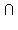
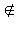
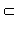
a α, b α = A , A a (чертеж 2.1.2). Допустим, что прямые a и b не скрещивающиеся, то есть они пересекаются. Тогда существует плоскость β, которой принадлежат прямые a и b . В этой плоскости β лежат прямая a и точка A . Поскольку прямая a и точка A вне ее определяют единственную плоскость, то β = α. Но b β и b α, следовательно, равенство β = α невозможно.

~~Теорема~~

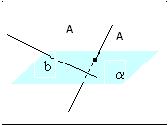
Две скрещивающиеся прямые имеют общий перпендикуляр, и при том только один. Он является общим перпендикуляром параллельных плоскостей, проходящих через эти прямые.

~~Доказательство~~

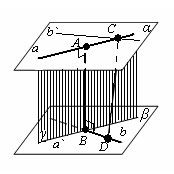
Пусть a и b – данные скрещивающиеся прямые. Проведем через них параллельные плоскости α и β. Прямые, пересекающие прямую a и перпендикулярные плоскости α, лежат в одной плоскости (γ). Эта плоскость пересекает плоскость β по прямой a`, параллельной a. Пусть B – точка пересечения прямых a` и b. Тогда прямая AB, перпендикулярная плоскости α, перпендикулярна и плоскости β, так как β параллельна α. Отрезок AB – общий перпендикуляр плоскостей α и β, а значит, и прямых a и b.
Докажем, что этот общий перпендикуляр единственный. Допустим, что у прямых a и b есть другой общий перпендикуляр CD. Проведем через точку С прямую b`, параллельную b. Прямая CD перпендикулярна прямой b, а значит, и b`. Так как она перпендикулярна прямой a, то она перпендикулярна плоскости α, а значит, параллельна прямой AB. Выходит, что через прямые AB и CD, как через параллельные, можно провести плоскость. В этой плоскости будут лежать наши скрещивающиеся прямые AC и BD, а это невозможно, что и требовалось доказать.

~~Расстоянием между двумя скрещивающимися прямыми называется длина их общего перпендикуляра.~~