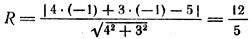Общее уравнение окружности в пространстве

Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром.

Если точка С — центр окружности, R — ее радиус, а М — произвольная точка окружности, то по определению окружности

Равенство (1) есть уравнение окружности радиуса R с центром в точке С.

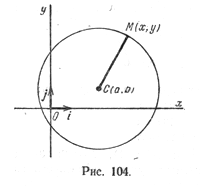
Пусть на плоскости задана прямоугольная декартова система координат (рис. 104) и точка С(а; b) — центр окружности радиуса R. Пусть М(х; у) — произвольная точка этой окружности.

Так как |СМ| = ( sqrt ), то уравнение (1) можно записать так:

(x — a) 2 + (у — b) 2 = R 2 (2)

Уравнение (2) называют общим уравнением окружности или уравнением окружности радиуса R с центром в точке (а; b). Например, уравнение

есть уравнение окружности радиуса R = 5 с центром в точке (1; —3).

Если центр окружности совпадает с началом координат, то уравнение (2) принимает вид

Уравнение (3) называют каноническим уравнением окружности.

Задача 1. Написать уравнение окружности радиуса R = 7 с центром в начале координат.

Непосредственной подстановкой значения радиуса в уравнение (3) получим

Задача 2. Написать уравнение окружности радиуса R = 9 с центром в точке С(3; —6).

Подставив значение координат точки С и значение радиуса в формулу (2), получим

(х — 3) 2 + (у — (—6)) 2 = 81 или (х — 3) 2 + (у + 6) 2 = 81.

Задача 3. Найти центр и радиус окружности

Сравнивая данное уравнение с общим уравнением окружности (2), видим, что а = —3, b = 5, R = 10. Следовательно, С(—3; 5), R = 10.

Задача 4. Доказать, что уравнение

является уравнением окружности. Найти ее центр и радиус.

Преобразуем левую часть данного уравнения:

Это уравнение представляет собой уравнение окружности с центром в точке (—2; 1); радиус окружности равен 3.

Задача 5. Написать уравнение окружности с центром в точке С(—1; —1), касающейся прямой АВ, если A (2; —1), B(— 1; 3).

Напишем уравнение прямой АВ:

или 4х + 3y —5 = 0.

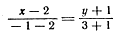
Так как окружность касается данной прямой, то радиус, проведенный в точку касания, перпендикулярен этой прямой. Для отыскания радиуса необходимо найти расстояние от точки С(—1; —1) — центра окружности до прямой 4х + 3y —5 = 0:

Напишем уравнение искомой окружности

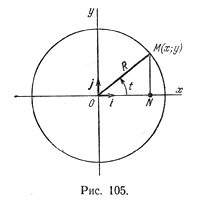
Пусть в прямоугольной системе координат дана окружность x 2 + у 2 = R 2 . Рассмотрим ее произвольную точку М(х; у) (рис. 105).

Пусть радиус-вектор OM > точки М образует угол величины t с положительным направлением оси Ох, тогда абсцисса и ордината точки М изменяются в зависимости от t

(0 2 = 3 cos 2 t, у 2 = 3 sin 2 t. Складывая эти равенства почленно, получаем

Видео:11. Прямая в пространстве и ее уравненияСкачать

Понятие об уравнении линии на плоскости и в пространстве. Уравнение окружности.

Уравнением линии на плоскости в декартовой системе координат называют уравнение: F(х;у)=0, которому удовлетворяют координаты (х;у) любой точки этой линии и не удовлетворяют координаты ни одной точки, которые не принадлежат ей.

Линия в пространстве задаётся в общем случае как линия пересечения некоторых поверхностей S₁ и S₂ .

называется уравнением линии в пространстве.

Окружностью называется линия, каждая точка М(х;у) на которой находится на одинаковом расстоянии от заданной точки , называемойцентром окружности. Величина называется радиусом окружности.

В прямоугольной системе координат уравнение окружности имеет вид

,

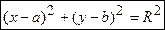
где (a; b) — координаты её центра, — радиус окружности.

В частности, если центр окружности совпадает с началом координат, т.е. a=0 , b=0 , то уравнение окружности примет вид:

Уравнение прямой. Различные виды уравнений прямой.

Общее уравнение прямой:

1.

, (2)

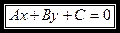
где 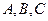— постоянные коэффициенты, причём и одновременно не обращаются в нуль .

Частные случаи этого уравнения:

— прямая проходит через начало координат;

— прямая параллельна оси ;

— прямая параллельна оси ;

— прямая совпадает с осью ;

— прямая совпадает с осью .

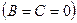
Нахождение углов между прямыми на плоскости. Условия параллельности и перпендикулярности прямых.

Если в пространстве заданы направляющий вектор прямой L

и уравнение плоскости

Ax + By + Cz + D = 0,

то угол между этой прямой и плоскостью можно найти используя формулу

Условия параллельности двух прямых:

а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

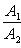
Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

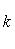
Это условие может быть записано также в виде

б) Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства

Уравнение прямой в пространстве: параметрические и канонические.

Если прямая проходит через две точки A(x₁, y₁, z₁) и B(x₂, y₂, z₂), такие что x₁ ≠ x₂, y₁ ≠ y₂ и z₁ ≠ z₂, то уравнение прямой можно найти используя следующую формулу

Параметрические уравнения прямой могут быть записаны следующим образом

	x = l t + x0
y = m t + y0
z = n t + z0

где (x₀, y₀, z₀) — координаты точки лежащей на прямой, — координаты направляющего вектора прямой.

Каноническое уравнение прямой в пространстве

Если известны координаты точки A(x₀, y₀, z₀) лежащей на прямой и направляющего вектора n = , то уравнение прямой можно записать в каноническом виде, используя следующую формулу

Уравнения плоскости.

Уравнение плоскости в прямоугольной системе координат Oxyz в трехмерном пространстве – это уравнение с тремя переменными x, y и z, которому удовлетворяют координаты любой точки заданной плоскости и не удовлетворяют координаты точек, лежащих вне данной плоскости.

Таким образом, уравнение плоскости обращается в тождество при подстановке в него координат любой точки плоскости. Если в уравнение плоскости подставить координаты точки, не лежащей в этой плоскости, то оно обратится в неверное равенство.

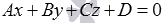
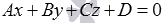
Всякое уравнение вида , где A, B, C и D – некоторые действительные числа, причем А, В и C одновременно не равны нулю, определяет плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве, и всякая плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве может быть задана уравнением вида .

Уравнение 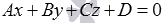называется общим уравнением плоскости в пространстве. Если не придавать числам А, В, С и D конкретных значений, то общее уравнение плоскости называют уравнением плоскости в общем виде.

Видео:Уравнение окружности (1)Скачать

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Прямоугольная декартова система координат на плоскости

Формула для расстояния между двумя точками координатной плоскости

Уравнение окружности на координатной плоскости

Видео:Уравнение прямой в пространстве. 11 класс.Скачать

Числовая ось

Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Прямоугольная декартова система координат на плоскости

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA₁ и AA₂ на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A₁ на числовой оси Ox , ординатой точки A называют координату точки A₂ на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.

Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .

Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.

Видео:Тема 12. Формула длины отрезка с заданными координатами концов. Уравнение окружностиСкачать

Формула для расстояния между двумя точками координатной плоскости

Утверждение 1 . Расстояние между двумя точками координатной плоскости

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.

что и требовалось доказать.

Видео:Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Уравнение окружности на координатной плоскости

Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:

Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A₀ (x₀ ; y₀) .

Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид

💥 Видео

УРАВНЕНИЕ ОКРУЖНОСТИСкачать

Лекция 25. Виды уравнений плоскости в пространстве.Скачать

ПРОСТОЙ СЕКРЕТ ДЛЯ НАЧИНАЮЩИХ! Реши алгебру за 12 минут — Уравнение ОкружностиСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Написать канонические и параметрические уравнения прямой в пространствеСкачать

Уравнение прямой в пространстве. Практическая часть. 11 класс.Скачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Уравнение окружностиСкачать

Уравнение окружности на примере задания из ОГЭ #математика #огэ #огэматематика #данирСкачать

12. Уравнения прямой в пространстве Решение задачСкачать

9 класс, 6 урок, Уравнение окружностиСкачать

13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать