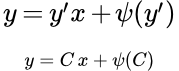Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5
Ввод распознает различные синонимы функций, как asin , arsin , arcsin
Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)
Список математических функций и констант :
• ln(x) — натуральный логарифм
• sh(x) — гиперболический синус
• ch(x) — гиперболический косинус
• th(x) — гиперболический тангенс
• cth(x) — гиперболический котангенс
• sch(x) — гиперболический секанс
• csch(x) — гиперболический косеканс
• arsh(x) — обратный гиперболический синус
• arch(x) — обратный гиперболический косинус
• arth(x) — обратный гиперболический тангенс
• arcth(x) — обратный гиперболический котангенс
• arsch(x) — обратный гиперболический секанс
• arcsch(x) — обратный гиперболический косеканс
Видео:Курс по ОДУ: Уравнения Клеро и Лагранжа | Занятие 8Скачать
Дифференциальное уравнение Клеро
Видео:Частное решение дифференциального уравнения. 11 класс.Скачать
Решение дифференциального уравнения Клеро
Рассмотрим уравнение Клеро:
(1)
Не трудно убедиться, что его общее решение имеет вид:
(2)
Действительно, поскольку – постоянная, то – тоже постоянная. Тогда дифференцируя (2) имеем:
;
(3) .
Подставляя (2) и (3) в (1), получаем тождество:
.
Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать
Особое решение дифференциального уравнения Клеро
Уравнение Клеро может иметь особое решение. Как известно, если общее решение дифференциального уравнения имеет вид:
,
то особое решение может получиться исключением из уравнений:
;
.
В нашем случае, решение (2) можно записать в виде:
.
Тогда
.
Тогда особое решение может получиться, исключением из уравнений:
;
.
Поскольку возможны посторонние решения, то после нахождения особого решения, необходимо проверить, удовлетворяет ли он исходному уравнению (1).
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать
Пример
Решить уравнение:
(1.1)
Это уравнение Клеро. Его общее решение имеет вид:
Ищем особое решение. Перепишем общее решение в виде:
.
Дифференцируем по :
.
Тогда особое решение может получиться исключением из уравнений:
(1.2) ;
(1.3) .
Исключаем . Из уравнения (1.3) имеем:
(1.4) .
Возводим в квадрат и преобразуем:
;
;
. Отсюда следует, что .
Извлекаем квадратный корень:
(1.5) .
Поскольку мы возводили в квадрат, то, возможно, (1.5) содержит лишние решения, которые не удовлетворяют (1.4). Сейчас мы примем (1.5), а отсев лишних решений сделаем в самом конце.
Подставим (1.4) и (1.5) в (1.2):
.
Итак, особые решения имеют вид:
(1.6) .
Теперь сделаем проверку, чтобы выяснить, удовлетворяет ли исходному уравнению (1.1):
(1.1) .
Находим производную (1.6) и выполняем преобразования:
;
;
.
Подставляем в (1.1):
(1.7) .
При , . Уравнение (1.7) принимает вид:
.
Оно выполняется, если взять нижний знак:
.
То есть при , .
При , . Уравнение (1.7) принимает вид:
.
Оно выполняется, если взять верхний знак:
.
То есть при , .
Общее решение уравнения имеет вид:
При уравнение имеет особое решение:
.
При уравнение имеет особое решение:
.
Автор: Олег Одинцов . Опубликовано: 24-08-2012 Изменено: 10-04-2016
Видео:Дифференциальные уравнения. 11 класс.Скачать
Дифференциальные уравнения по-шагам
Видео:Решение уравнения ЛагранжаСкачать
Результат
Примеры дифференциальных уравнений
- Простейшие дифференциальные ур-ния 1-порядка
- Дифференциальные ур-ния с разделяющимися переменными
- Линейные неоднородные дифференциальные ур-ния 1-го порядка
- Линейные однородные дифференциальные ур-ния 2-го порядка
- Уравнения в полных дифференциалах
- Решение дифференциального уравнения заменой
- Смена y(x) на x в уравнении
- Другие
Указанные выше примеры содержат также:
- квадратные корни sqrt(x),
кубические корни cbrt(x) - тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - показательные функции и экспоненты exp(x)
- обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x) - натуральные логарифмы ln(x),
десятичные логарифмы log(x) - гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x) - обратные гиперболические функции:
asinh(x), acosh(x), atanh(x), actanh(x) - число Пи pi
- комплексное число i
Правила ввода
Можно делать следующие операции
2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5
Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:
🎦 Видео
Решение уравнения КлероСкачать
ЛОДУ 2 порядка c постоянными коэффициентамиСкачать
Общее и частное решение дифференциального уравненияСкачать
11. Уравнения в полных дифференциалахСкачать
Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать
Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать
Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать
9 класс, 7 урок, Уравнение прямойСкачать
Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать
Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать
9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать
