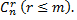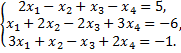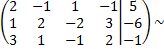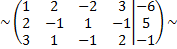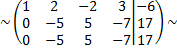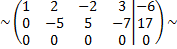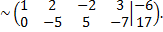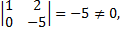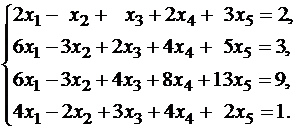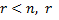
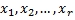
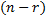
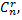
Общее базисное и частное решение систем линейных алгебраических уравнений (5 видео)

Общее, базисное и частное решение систем линейных алгебраических уравнений.

Пусть переменных называются основными (или базисными), если определитель матрицы из коэффициентов при них (т.е. базисный минор) отличен от нуля. Остальные переменных называются неосновными (или свободными). Каждому разбиению переменных на основные и неосновные соответствует одно базисное решение, а число способов разбиения не превосходит числа сочетаний то и базисных решений имеется не более

Совместная система линейных уравнений с переменными имеет бесконечное множество решений, среди которых базисных решений конечное число, не превосходящее

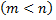
Достоинства метода Гаусса по сравнению с другими:

— менее трудоемкий метод;

— позволяет однозначно установить, совместна система или нет и в случае совместности найти ее решение;

— дает возможность найти максимальное число линейно независимых уравнений – ранг матрицы системы.

Рассмотрим пример. Найти решение системы линейных алгебраических уравнений

Составим расширенную матрицу по данной системе

поменяем местами первую и вторую строку

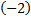
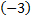
умножим первую строку на и сложим со второй строкой; умножим первую строку на и сложим с третьей строкой

умножим вторую строку на 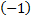и сложим с третьей строкой

последняя строка вычеркивается, так как все ее элементы равны нулю

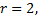
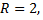
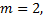
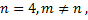
Ранг основной матрицы ранг расширенной матрицы следовательно, система совместна. Число строк в основной матрице число столбцов в основной матрице следовательно, система имеет множество решений.

Выявим базисные переменные

следовательно, 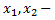базисные переменные, тогда

Видео:Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Как найти общее и частное решение системы линейных уравнений

Пример 2. Исследовать совместность, найти общее и одно частное решение системы

Решение. Переставим первое и второе уравнения, чтобы иметь единицу в первом уравнении и запишем матрицу B.

Получим нули в четвертом столбце, оперируя первой строкой:

Теперь получим нули в третьем столбце с помощью второй строки:

Третья и четвертая строки пропорциональны, поэтому одну из них можно вычеркнуть, не меняя ранга:
Третью строку умножим на (–2) и прибавим к четвертой:

Видим, что ранги основной и расширенной матриц равны 4, причем ранг совпадает с числом неизвестных, следовательно, система имеет единственное решение:
-x₁=-3 → x₁=3; x₂=3-x₁ → x₂=0; x₃=1-2x₁ → x₃=5.
x₄ = 10- 3x₁ – 3x₂ – 2x₃ = 11.

Пример 3. Исследовать систему на совместность и найти решение, если оно существует.

Решение. Составляем расширенную матрицу системы.

Переставляем первые два уравнения, чтобы в левом верхнем углу была 1:
Умножая первую строку на (-1), складываем ее с третьей:

Умножим вторую строку на (-2) и прибавим к третьей:

Система несовместна, так как в основной матрице получили строку, состоящую из нулей, которая вычеркивается при нахождении ранга, а в расширенной матрице последняя строка останется, то есть r_B > r_A.

Задание. Исследовать данную систему уравнений на совместность и решить ее средствами матричного исчисления.
Решение

Пример. Доказать совместимость системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса; 2) методом Крамера. (ответ ввести в виде: x1,x2,x3)
Решение:doc:doc:xls
Ответ: 2,-1,3.

Пример. Дана система линейных уравнений. Доказать ее совместность. Найти общее решение системы и одно частное решение.
Решение
Ответ:x₃ = — 1 + x₄ + x₅; x₂ = 1 — x₄; x₁ = 2 + x₄ — 3x₅

Задание. Найти общее и частное решения каждой системы.
Решение. Исследуем эту систему по теореме Кронекера-Капелли.
Выпишем расширенную и основную матрицы:

1	1	14	0	2	0
3	4	2	3	0	1
2	3	-3	3	-2	1
x₁	x₂	x₃	x₄	x₅

Здесь матрица А выделена жирным шрифтом.
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Умножим 1-ую строку на (3). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:

0	-1	40	-3	6	-1
3	4	2	3	0	1
2	3	-3	3	-2	1

Умножим 2-ую строку на (2). Умножим 3-ую строку на (-3). Добавим 3-ую строку к 2-ой:

0	-1	40	-3	6	-1
0	-1	13	-3	6	-1
2	3	-3	3	-2	1

Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:

0	0	27	0	0	0
0	-1	13	-3	6	-1
2	3	-3	3	-2	1

Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), причем этот минор принадлежит как основной матрице, так и расширенной, следовательно rang(A) = rang(B) = 3. Поскольку ранг основной матрицы равен рангу расширенной, то система является совместной.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x₁,x₂,x₃, значит, неизвестные x₁,x₂,x₃ – зависимые (базисные), а x₄,x₅ – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.

0	0	27	0	0	0
0	-1	13	-1	3	-6
2	3	-3	1	-3	2
x₁	x₂	x₃	x₄	x₅

Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
27x₃ =
— x₂ + 13x₃ = — 1 + 3x₄ — 6x₅
2x₁ + 3x₂ — 3x₃ = 1 — 3x₄ + 2x₅
Методом исключения неизвестных находим:
Получили соотношения, выражающие зависимые переменные x₁,x₂,x₃ через свободные x₄,x₅, то есть нашли общее решение:
x₃ = 0
x₂ = 1 — 3x₄ + 6x₅
x₁ = — 1 + 3x₄ — 8x₅
Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Система является неопределенной, т.к. имеет более одного решения.

Задание. Решить систему уравнений.
Ответ😡₂ = 2 — 1.67x₃ + 0.67x₄
x₁ = 5 — 3.67x₃ + 0.67x₄
Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Система является неопределенной

Пример. Проверить совместность линейной системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) методом Гаусса.
Решение: Проверяем совместность системы с помощью теоремы Кронекера — Капелли. Согласно теореме Кронекера — Капелли, из того, что следует несовместность исходной системы.
Ответ: система не совместна.
Решение

Видео:Базисные решения систем линейных уравнений (03)Скачать

Разрешенная система уравнений. Общее, частное и базисное решения

Определение. Неизвестная х, называется разрешенной для системы уравнений, если она входит в одно из уравнений системы с коэффициентом +1, а в остальные уравнения не входит, т.е. входит с коэффициентом, равным нулю.

Определение. Неизвестная х. называется разрешенной, если в системе линейных уравнений (2.2) существует s-e уравнение, содержащее это неизвестное с коэффициентом a_sj = 1, а в остальных уравнениях системы (2.2) коэффициенты при этом неизвестном равны нулю, т.е. а- = 0 при / ф s.

Определение. Система уравнений называется разрешенной, если каждое уравнение системы содержит разрешенную неизвестную, отличную от разрешенных переменных в остальных уравнениях.

Разрешенные неизвестные, взятые по одной из каждого уравнения системы, образуют полный набор разрешенных неизвестных системы. Заметим, что полный набор разрешенных неизвестных определяется неоднозначно.

Разрешенные неизвестные, входящие в полный набор, называют также базисными переменными, а не входящие в полный набор — свободными переменными.

В общем случае разрешенная система уравнений имеет вид

Определение. Общим решением разрешенной системы уравнений называется совокупность выражений разрешенных неизвестных через свободные члены (правые части) и свободные неизвестные:

Определение. Частным решением системы уравнений называется решение, получающееся из общего решения при конкретных значениях свободных неизвестных.

Определение. Базисным решением называется частное решение, получающееся из общего при нулевых значениях свободных неизвестных.

Определение. Базисное решение называется вырожденным, если число его координат, отличных от нуля, меньше числа разрешенных неизвестных.

Определение. Базисное решение называется невырожденным, если число его координат, отличных от нуля, равно числу разрешенных неизвестных системы, входящих в полный набор.

Любое общее решение системы представляет собой совокупность соотношений, используя которые можно получить любое частное решение из множества всех возможных частных решений системы.

Разрешенная система уравнений всегда совместна; причем если система не имеет свободных неизвестных, то она является определенной; если же имеется хотя бы одна свободная неизвестная, то система является неопределенной.

Пример 2.3. Найти общее, базисное и какое-либо частное решение системы

Решение. Система является разрешенной, поэтому, включив в набор разрешенных неизвестных х и х₂, записываем общее решение

Если включить в набор разрешенных неизвестных х₅ вместо х_<, то можно записать другое общее решение

Найдем частное решение, соответствующее значениям свободных переменных х₃ = 0, х₄ = 1, х₅ = 2, для этого, подставляя в первое общее решение заданные значения свободных неизвестных, получим

Запишем частное решение Х_ч = (9, 24, 0, 1, 2).

Если принять свободные переменные равными нулю х₃ = х₄ = ,r_g = О, то из первого общего решения получим ту = 10, х₂ = 20 и запишем базисное решение Х₆ = (10, 20, 0, 0, 0).

Если для какой-либо заданной системы уравнений получена равносильная ей разрешенная система, то общее, частное и базисное решения этой разрешенной системы являются также решениями исходной системы.

Е1еобходимо заметить, что любые две разрешенные системы уравнений, равносильные заданной системе, совпадают, если они имеют одни и те же разрешенные, а следовательно и свободные, неизвестные.