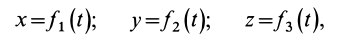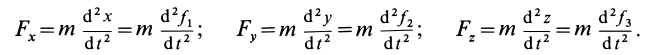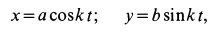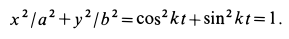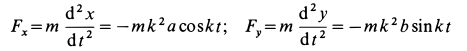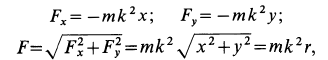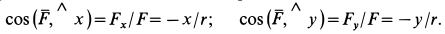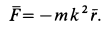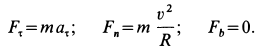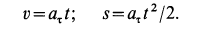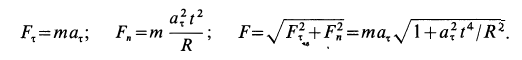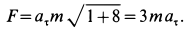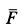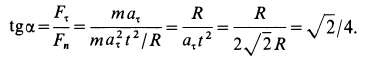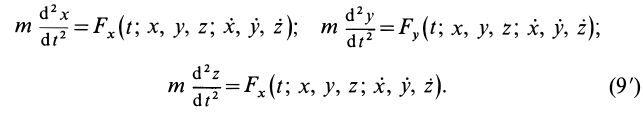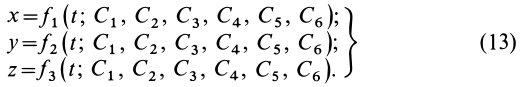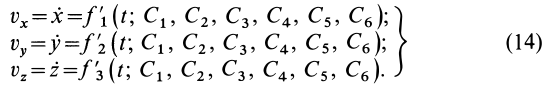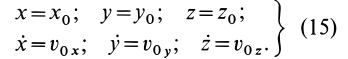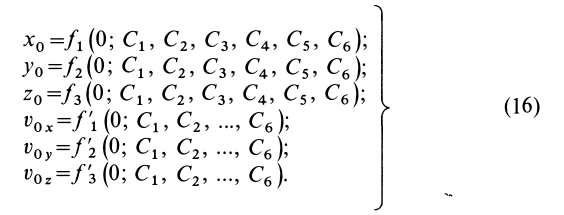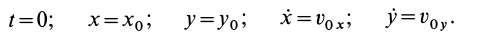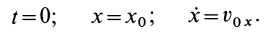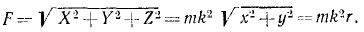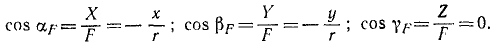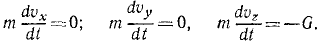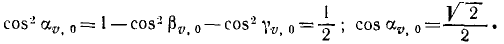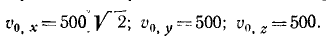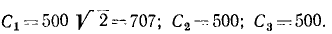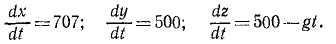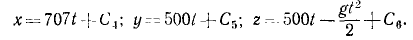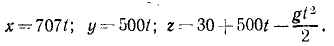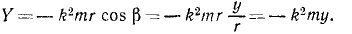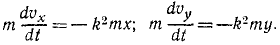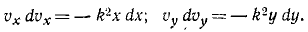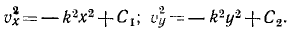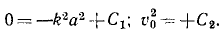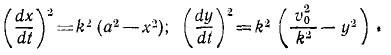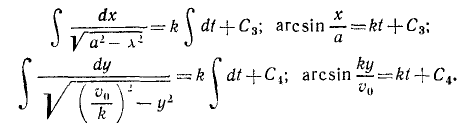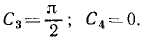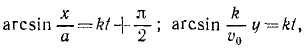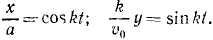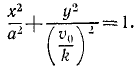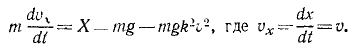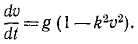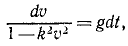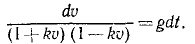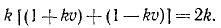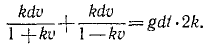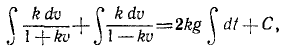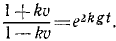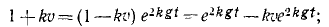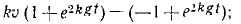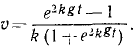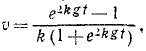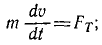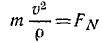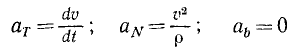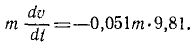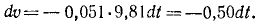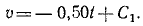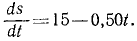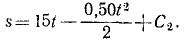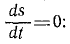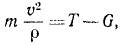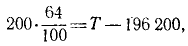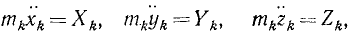Обратные задачи для дифференциальных уравнений

Видео:Решение физических задач с помощью дифференциальных уравненийСкачать

«Обратные задачи для дифференциальных уравнений» как компонент вычислительной информатики в системе подготовки будущих учителей информатики

Международная конференция «Обратные и некорректные задачи математической физики»,
посвященная 75-летию академика , 20-25 августа 2007 г., Новосибирск, Россия

«Обратные задачи для дифференциальных уравнений»
как компонент вычислительной информатики
в системе подготовки будущих учителей информатики

* Казахский национальный педагогический университет им. Абая

г. Алматы, Республика Казахстан

Вычислительная информатика – одно из научных «направлений информатики, включающее отображение алгоритмов на архитектуру вычислительных систем, прикладное программное обеспечение вычислительных задач и методологию численного моделирования процессов и явлений»[1]. Именно с элементов вычислительной информатики (элементов алгоритмизации, вычислительной математики, программирования решения вычислительных задач и др.) начиналось внедрение информатики в систему образования еще в рамках первых факультативных курсов. А по мере того, как компьютеры становились способными решать все более сложные задачи, данное направление приобретало все большее значение и важность. И сегодня, как много лет назад, вычислительная информатика занимает особое место в решении задач, возникающих в различных прикладных областях, поскольку и сегодня «самые совершенные и дорогие компьютеры используются для решения задач с отчетливой математической подоплекой; в широком смысле все эти задачи можно назвать задачами математического моделирования». Но в настоящее время ее значение определяется не только увеличивающимися возможностями применения математического моделирования и вычислительных методов в различных прикладных научных направлениях и, как следствие, в вузовском учебном процессе, а и проникновением ее элементов, для обеспечения фундаментальности курса информатики, в среднее образование, т. е. в сферу профессиональной деятельности учителя. И переход к профильному обучению с выделением физико-математического, естественнонаучного и информационно-технологического направлений в старших классах существенно расширяет эту сферу.

Вычислительная информатика затрагивает многие вопросы и технического оснащения, и прикладного программного обеспечения вычислительных задач, а также алгоритмических тенденций и моделирования, столь необходимые будущему учителю информатики в профессиональной деятельности. В частности, затрагивает много важных для будущего учителя информатики идей и методов, включая точность численного представления, анализ ошибок, численные методы, параллельные архитектуры и алгоритмы, моделирование и визуализацию научных данных.

Необходимо заметить, что основные положения данного направления информатики отчасти находят отражение в базовом курсе информатики в рамках разных ее разделов и тем, таких как теоретическая информатика, средства информатизации и информационные технологии. Однако будущий учитель информатики не может ограничиться только этим. Ему необходимы более глубокие и обширные знания в вопросах вычислительной информатики. И эту необходимость, прежде всего, диктуют современные требования, предъявляемые к профессиональной подготовке учителя информатики. Будущий учитель информатики должен быть готов как к ведению стандартного курса информатики в общеобразовательной школе, так и к преподаванию специализированных курсов при профильной и уровневой дифференциации обучения в школе. Кроме того, что не менее важно, для того, чтобы в школах обучение информатике не отставало от прогресса, профессиональная подготовка будущего учителя информатики должна осуществляться не только для текущего момента, но и с перспективой на будущее.

Не вызывает сомнений, что изучение вопросов, связанных с данным направлением информатики должно способствовать формированию у будущего учителя информатики современного научного мировоззрения, соответствующей информационной, математической культуры, а также овладению методологией анализа окружающей действительности с позиций единого информационного подхода. Должно способствовать его обеспечению необходимым для будущей профессиональной деятельности инструментарием, рассчитанным на длительную перспективу и достаточно инвариантным по отношению к возможным изменениям в области информационных технологий и вычислительной техники. Поэтому фундаментальная подготовка будущих учителей информатики в области вычислительной информатики позволит им, на наш взгляд, полноценным образом подготовить подрастающее поколение к жизни в информационном обществе.

Проблематика численного моделирования, «составляя одну из основ информатики, теснейшим образом примыкает и к вычислительной математике, и к программированию, а в плане построения математических и информационных моделей – ко всем наукам, где возможно применение ЭВМ. В связи с этим налицо прямая связь и некоторый непрерывный переход вычислительной информатики (четкой границы установить невозможно) с вычислительной математикой, с одной стороны, и с многочисленными предметными науками (через математические и информационные модели) – с другой» [1]. Поэтому вычислительную информатику, не претендуя на полноту и строгость, можно определить как комплекс дисциплин, связанных посредством математических и информационных моделей, ядром которого является вычислительная математика.

А вычислительная математика – «одна из важнейших дисциплин профессиональной подготовки будущего учителя, которая развивает идеи численного решения задач, возникающих в процессе компьютерного математического моделирования реальных явлений в различных предметных сферах» [2].

Безусловно, рассматриваемое направление информатики не исчерпывается одной только данной дисциплиной, основные ее положения должны быть развиты дальше в других курсах учебного плана подготовки учителей информатики («методы оптимизации», «исследование операций» и др.). Так, в Казахском национальном педагогическом университете им. Абая дальнейшее развитие вычислительная информатика получает также при изучении дисциплин по выбору, таких как «параллельные вычисления», «машинная арифметика и вопросы устойчивости вычислительных алгоритмов», «теория разностных схем», «обратные задачи для дифференциальных уравнений», которые занимают важное место в системе учебных мероприятий по дополнению и углублению профессиональных знаний будущего учителя информатики.

Представления об информационном, в частности математическом, моделировании, умение составлять модели реальных процессов и работать с ними, используя адекватные средства, в настоящее время приобретают общекультурную и общеобразовательную ценность и открывают возможности для формирования у студентов представлений о роли моделей и моделирования в различных областях науки и техники. Информационное моделирование занимает одно из ведущих мест среди методов познания, используемых в настоящее время наукой, и имеет большое значение для формирования научной картины мира. А в последнее время с развитием информатики как научной дисциплины, информационное моделирование, как инструмент познания, завоевывает все новые и новые позиции в различных областях деятельности человека, получает все более широкое распространение при изучении окружающей действительности. Поэтому специалистам различных направлений, тем более будущим учителям информатики необходимо не только владеть концепциями и методами информационного моделирования, но и иметь представление об инструментарии, применяемом при моделировании.

Являясь одной из приоритетных содержательно-методических линий курса информатики, идеи и методы теории информационного моделирования в явной или неявной форме пронизывают практически все учебные дисциплины. Безусловно, что обучение информационному моделированию является одним из путей усиления фундаментальной подготовки будущих учителей информатики.

В курсе «обратные задачи для дифференциальных уравнений» рассматривается масса интересных и содержательных задач и современных математических моделей, при решении которых широко используются средства вычислительного эксперимента. Сами же обратные задачи – это, в принципе, определение неизвестных параметров математической модели путем сопоставления наблюдаемых данных и результатов моделирования. Поэтому изучение дисциплины «обратные задачи для дифференциальных уравнений», несомненно, позволит обогатить представления об информационном моделировании с математической точки зрения, обогатить представления о вычислительном эксперименте – современной технологии и методологии проведения теоретических исследований и расширить спектр, рассматриваемых на ЭВМ задач. Даст еще один инструмент для познания мира, в котором мы живем, позволит сформировать образное и научное представление о реальном физическом пространстве.

Содержание дисциплины включает следующие разделы:

· математическое моделирование как способ изучения окружающего мира;

· моделирование протекающих в окружающем нас мире процессов и явлений в виде дифференциальных уравнений как один из эффективных способов изучения этих процессов;

· роль теории обратных задач в естественных науках и ее современные приложения;

· особенности и типы обратных задач и их классификация;

· методы исследования обратных задач для дифференциальных уравнений;

· корректность прямых и обратных задач для дифференциальных уравнений;

· системный подход и методология в обратных задачах математической физики;

· познавательная сила обратных задач;

· обратные задачи для дифференциальных уравнений в частных производных, в том числе обратные задачи магнитотеллурического зондирования для наклонно падающих неоднородных плоских волн;

· численные методы решения обратных задач для дифференциальных уравнений.

Изучение их позволит познакомить студентов с увлекательной проблематикой теории обратных задач, способствуя выработке у студентов широкого универсального взгляда на окружающую действительность, позволит расширить возможности информационного моделирования, несмотря на то, что им для решения отдельных проблем могут потребоваться и более глубокие фундаментальные знания по основным математическим дисциплинам. Но, важно то, что изучение их наряду с вопросами, рассматриваемыми в вычислительной математике должно обеспечить учителю все потребности школьных курсов математики, физики, факультативных курсов, других форм дополнительной и внеурочной работы с учащимися. В том числе, естественно, и потребности вычислительной информатики.

Курс «обратные задачи для дифференциальных уравнений», с одной стороны, наряду с изучением строгой математической теории методов вычислений, призван продемонстрировать широкие применения математического аппарата для изучения процессов и явлений реальной действительности, с другой – показать богатство возможностей компьютерных информационных подходов к действительности и их принципиальную ограниченность. Изучение его создает системное представление о мире и имеет огромное значение для формирования научного мировоззрения, что является основной целью общего образования.

Таким образом, подготовка будущего учителя информатики по «обратным задачам для дифференциальных уравнений», как одной из дисциплин, относящихся к направлению вычислительная информатика, позволит внести значительный вклад в формирование современного научного мировоззрения, развитие общеучебных навыков работы с информацией и подготовку к профессиональной деятельности в информационном обществе. В связи с этим, необходимо развивать и совершенствовать методическую систему обучения будущих учителей информатики по вычислительной информатике и в вышеуказанном направлении тоже.

Ильин информатика: открытие науки.– Новосибирск: Наука. Сиб. отделение, 1991.–198с.

2. , , Численные методы.– М.: Изд. центр «Академия», 2004. – 384с.

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Математическое моделирование и обратные задачи Текст научной статьи по специальности « Математика»

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Аннотация научной статьи по математике, автор научной работы — Цей Раджеп, Шумафов Магомет Мишаустович

В работе выделяется значимость применения обратных задач при математическом моделировании . Приводятся примеры применения обратных задач в разных областях науки. Упоминаются основные труды отечественных и зарубежных ученых, внесших наиболее весомый вклад в развитие теории обратных задач .

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Похожие темы научных работ по математике , автор научной работы — Цей Раджеп, Шумафов Магомет Мишаустович

Видео:Решение задачи Коши дифференциального уравнения #maths #calculus #differentialequation #algebraСкачать

Текст научной работы на тему «Математическое моделирование и обратные задачи»

УДК 518.6 : 517.9 ББК 22.181 Ц 32

Р. Цей, М.М. Шумафов

Математическое моделирование и обратные задачи

В работе выделяется значимость применения обратных задач при математическом моделировании. Приводятся примеры применения обратных задач в разных областях науки. Упоминаются основные труды отечественных и зарубежных ученых, внесших наиболее весомый вклад в развитие теории обратных задач.

Математическое моделирование, идентификация, дифференциальные уравнения, обратная задача.

Для изучения объектов или процессов, протекающих в окружающем нас мире, широко используются методы математического моделирования. Математические модели являются мощным средством познания окружающего мира. При этом следует заметить, что построенная математическая модель (какая бы сложная она не была) не может отразить все многообразные и сложные черты изучаемого явления. Обычно исследователь изучает только какую-нибудь сторону того или иного процесса или явления. При моделировании что-то является главным, а что-то — второстепенным, чем можно пренебречь. Поэтому исследователь сознательно огрубляет изучаемый процесс и идет на сознательное упрощение изучаемого явления. В результате, он имеет дело с идеализированным математическим образом реального процесса, происходящего в окружающем мире. Такая идеализация мотивируется тем, что наиболее часто оказывается, что фундаментальные законы природы получаются именно при максимальной идеализации (что с первого взгляда может оказаться удивительным). Например, первый закон Ньютона (один из самых основных законов физики) получен в предположении, что тело движется в пространстве, где нет других тел. Или, скажем, уравнение газодинамики или уравнение распространения тепла — они выведены тоже как раз в предположении идеальности газа и абсолютной однородности бруса, в котором распространяется тепло. Эти уравнения, как известно, хорошо описывают в приемлемом для практики приближении реальные процессы.

Одним из эффективных способов изучения математическими методами процессов, протекающих в окружающем нас мире, является моделирование этих процессов в виде дифференциальных уравнений. Для их составления нужно знать только локальные связи и не нужна информация обо всем явлении в целом. Это существенно упрощает задачу, так как в малом — все линейно. Например, при составлении уравнения колебаний струны:

32и_ 23 и 3 ¿2 3 х2

(где а _ — , Т — натяжение струны, постоянное в рамках приближения малых колебаний; р —

плотность струны) мы априори не знаем, что струна в целом будет совершать колебательные движения. Мы используем лишь упругий характер сил сцепления отдельных элементов струны. В результате, полученное с использованием лишь локальных свойств струны, уравнение определяет решение, которое носит колебательный характер. С помощью этого решения можно провести качественный и количественный анализ движения струны в целом, что хорошо соответствует реально происходящему явлению. В данном случае вся информация о поведении объекта в целом заложена в информации о его локальном поведении. На основе этой информации строится математическая модель, которая дает возможность изучать явление в целом.

Как правило, получаемые при математическом моделировании дифференциальные уравнения содержат коэффициенты, связанные с физическими характеристиками среды, в которой протекают эти процессы. (Например, в вышеупомянутом уравнении колебаний струны

— это а _ „ — . Или в хорошо известном уравнении маятника (при некоторой идеализации)

dj- + 0 2 sin j = 0 — это о = — , где l — длина маятника, m — масса материальной точки).

Весьма часто на практике встречаются такие ситуации, когда объект исследования бывает труднодоступным или недоступным вовсе, вследствие чего коэффициенты, присутствующие в конкретной математической модели, являются неизвестными функциями. Так, например, при поиске полезных ископаемых необходима информация о внутреннем строении Земли; при разработке и эксплуатации нефтегазовых месторождений необходима информация о

параметрах нефтегазоносного пласта; при диагностике различных заболеваний в медицине нужна информация о внутренних органах человека и т.д.

Непосредственное изучение внутреннего строения Земли с помощью бурения ограничено. Поэтому главную роль здесь играют геофизические методы, основанные на изучении на земной поверхности какого-либо физического поля, которое несет информацию о глубинном строении Земли. Таким полем, в частности, является электромагнитное поле, создаваемое с помощью специального источника электромагнитных колебаний. Другими словами, по измеренному электромагнитному полю на поверхности Земли, требуется определить электромагнитные параметры внутри Земли.

В начале XX века немецкими геофизиками Г. Герглотцем и Е. Вихертом была рассмотрена следующая задача: нельзя ли, располагая картиной движения фронтов сейсмических волн по поверхности Земли, порожденных землетрясениями, найти скорость распространения сейсмических волн внутри Земли? Поставленная задача (и подобные им задачи), по сути дела, является задачей определения неизвестной функции (скорости распространения сейсмических волн) из соответствующего дифференциального уравнения по известной частичной информации о решении этого уравнения. Подобные задачи тоже, по своей сути, являются задачами определения неизвестных коэффициентов, входящих в дифференциальное уравнение.

Таким образом, потребности практики часто приводят к задачам определения коэффициентов дифференциальных уравнений (обыкновенных или в частных производных), правой части, начальных условий по некоторым известным функционалам его решения. Такие задачи, в отличие от обычных для дифференциальных уравнений, когда уравнение задано, а требуется отыскать его решение (прямые задачи), получили название обратных задач математической физики. Термин «обратная задача» был введен выдающимися российскими математиками М.М. Лаврентьевым и В.Г. Романовым 5.

Деление задач на прямые и обратные обусловлено причинно-следственной связью. Проиллюстрируем это на примере.

Пусть на какую-нибудь физическую систему оказывается внешнее воздействие. Если известны параметры системы и характер воздействия, то можно ставить задачи об описании отклика системы на него. Это прямые задачи. Эти задачи представляют собой задачи отыскания следствий по известным причинам. Иными словами, в этих задачах по заданным локальным законам (физическим, химическим, биологическим, экономическим и т.д.), действующим внутри исследуемой системы, нужно ответить на вопрос: как будет вести себя система в целом? В этом случае все параметры исследуемой системы известны и изучается ее эволюция во времени.

Представим теперь ситуацию, когда наблюдатель изучает систему по ее отклику на внешнее воздействие и ставит целью восстановить параметры системы. Подобные задачи относятся к обратным и связаны они с обращением причинно-следственной связи -отысканием неизвестных причин по известным следствиям. При этом, как правило, «причины» конкретизируются в виде неизвестных коэффициентов, правой части, начальных условий дифференциального уравнения. В качестве же «следствий» выступают функционалы от решения дифференциального уравнения. Примерами обратных задач являются задачи:

1) определения характеристик источников поля в некоторых точках или областях пространства по результатам измерения параметров поля,

2) восстановления входного сигнала по реакции на выходе прибора,

3) определения параметров нефтегазоносного пласта по натурным наблюдениям (через определенные периоды времени) значений давления, насыщенности и др. контрольных скважин.

В этих и подобных им задачах реальные процессы, протекающие в исследуемом объекте, неизвестны, но имеются косвенные наблюдения. По результатам этих наблюдений пытаются найти определяющие параметры модели, управляющие поведением объекта.

Таким образом, обратные задачи — это определение параметров модели путем сопоставления наблюдаемых данных и результатов моделирования. Эту процедуру называют идентификацией математической модели.

Обратные задачи возникают не только в математике и физике, но и в других областях науки (геофизика, астрофизика, инженерные науки, теоретическая физика, медицина и др.) и в различных сферах человеческого бытия. Например, в археологии исследователи сталкиваются с решением обратных задач, направленных на восстановление исторических событий на основе ограниченного объема зарегистрированных «следствий». В медицине все задачи диагностики также относятся к обратным задачам. Например, наблюдая те или иные параметры состояния человека, требуется определить причины этого состояния (болезни).

Основы теории и практики исследования обратных задач математической физики были заложены и развиты в фундаментальных работах выдающихся ученых современности:

A.Н. Тихонова 11, А.С. Алексеева [10], М.М. Лаврентьева 1, В.Г. Романова [1, 2, 4, 5],

B.А. Амбарцумяна [15], Г. Борга [16], И.М. Гельфанда [17], Б.М. Левитана [17], М.Г. Крейна [18] и др.

В дальнейшем, развитая ими методика исследования обратных задач была применена в исследованиях широкого круга обратных задач их учениками и последователями: Ю.Е. Аниконовым, А.В. Баевым, А.С. Барашковым, С.П. Белинским, А.С. Благовещенским, Б.А. Бубновым, А.Л. Бухгеймом, Н.П. Волковым, В.И. Дмитриевым, А.Д. Искендеровым,

C.И. Кабанихиным, А.Л. Карчевским, В.С. Корниловым, М.В. Клибановым, С.В. Мартаковым, Б.С. Парийским, В.И. Прийменко, А.И. Прилепко, Т.П. Пухначевой, М.Г. Савиным, А.М. Федотовым, В.А. Чевердой, В.Г. Чередниченко, В.Г. Яхно и др. Целый ряд результатов в этом направлении получили в последние десятилетия зарубежные авторы, такие как Д.Г. Берриман, М. Грацелли, Р.Р. Грин, Р. Барридж, И.М. Ген, А. Лоренци, Д.К. Лиу, А. Ракеш, П. Сакс, В.В. Саймз, Ф. Сантоза и др. 14.

Подводя итог сказанному выше, приведем общую математическую постановку обратной задачи.

Пусть некоторый объект (явление или процесс в окружающем мире) подлежит изучению. Для этого ставится эксперимент. При этом типичной является ситуация, когда интересующие исследователя количественные характеристики объекта x(s) недоступны для

непосредственного наблюдения и имеется лишь некоторая косвенная информация y(t) о них.

Математически обратная задача состоит в отыскании функции x(s) по функции y(t)

(получаемой из эксперимента или наблюдений) из уравнения вида:

где A есть некоторый оператор, устанавливающий причинно-следственную связь между x(s) и y(t) (y(t) — «следствие», x(s) — «причина»). Здесь A определяется природой изучаемого объекта и используемым при этом арсеналом экспериментальных методов и приемов. В (1) y(t) есть следствие, причинно обусловленное заданием оператора A и модели x(s). Требуется определить количественные характеристики объекта x(s) по результатам наблюдений y(t).

Другими словами, требуется решить операторное уравнение (1) относительно x(s) при известном y(t).

Примеры обратных задач

1. Простейшей обратной задачей является «школьная» задача об определении коэффициентов квадратного уравнения по известным его корням. И, вообще, если известны корни алгебраического уравнения n-ой степени, то коэффициенты (=решение обратной задачи) этого уравнения определяются по формулам Виета.

2. Движение материальной точки массы т в соответствии с законом Ньютона описывается дифференциальным уравнением:

Здесь х(1) — положение точки в момент времени I, ¥(^ — сила, действующая на точку. Будем считать, что начальное положение точки и ее скорость известны. Предположим, что известно положение точки х(1) как функция времени. Обратная задача состоит в определении зависимости ¥=¥(1) по известному закону х().

3. Обратной задачей является также задача об определении коэффициентов системы линейных дифференциальных уравнений по известным его линейно-независимым решениям [22, с. 131].

4. На поверхности исследуемого объекта имеются источник колебаний и их приемник, который регистрирует волны как непосредственно пришедшие от источника, так и отраженные от дефекта (полость, трещина и т.д.). Обратная задача состоит в определении по известным амплитуде и фазе регистрируемого сигнала геометрической границы дефекта и выявлении его структуры (рис. 1).

5. Предположим, что в пространстве расположено недоступное для непосредственного наблюдения тело. Однако его можно облучать с различных сторон и регистрировать тень на некоторой плоскости а, перпендикулярной направлению облучения (рис. 2). Обратная задача состоит в определении формы тела по семейству его теней.

Математическая модель рассматриваемого процесса выгладит так:

Здесь ¥ — начальная интенсивность прямолинейного луча L, а 11 — интенсивность после прохождения тела, Д.х) — коэффициент поглощения рентгеновских лучей в точке х.

Таким образом, в результате облучения по разным направлениям мы знаем интегралы от функции Д.х) по всевозможным прямым L. Обратная задача состоит в определении функции Д(х) по совокупности этих интегралов. Решение этой математической проблемы составляет фундамент современной компьютерной томографии.

Основополагающая работа, в которой была получена формула, позволяющая восстанавливать функцию по набору ее проекций, была получена в 1917 году австрийским математиком И. Радоном, а практическое ее использование началось лишь полвека спустя.

6. Простейшая линейная модель прибора, регистрирующего какие-либо физические поля (электромагнитные, тепловые), может быть описана следующим образом.

На вход прибора поступает сигнал и@), на выходе регистрируется сигнал Д(1), которые связаны зависимостью:

где К(% s) — известная функция. Обратная задача состоит в определении входного сигнала и($ по регистрируемой прибором функции (), то есть в нахождении решения интегрального уравнения (2).

О характерных особенностях обратных задач

Обратные задачи обладают рядом неприятных с математической точки зрения особенностей.

Первое. Как правило, обратные задачи нелинейны, то есть неизвестная функция или неизвестный параметр входит в операторное или функциональное уравнение нелинейным образом.

Второе. Решения обратных задач обычно неединственны. Для обеспечения единственности часто необходимо требовать избыточности экспериментальной информации. Например, при определении формы полости в теле при помощи регистрации отраженных волн необходимо знание отраженного поля в некотором диапазоне изменения частоты ® 0 е [® г,ю 2]

. На практике же мы можем измерить отраженное поле в достаточно большом, но конечном наборе частот на отрезке [а, ш2], что может привести к неединственности восстановления формы полости, появлению посторонних или, как называют их в ультразвуковой диагностике, «фантомных» решений.

Третье. Обратные задачи не являются корректными. Понятие корректной задачи, являющееся одним из важнейших понятий современной математики, было сформулировано французским математиком Ж. Адамаром (1923). Оно означает, что:

1) решение задачи существует,

2) решение единственно на некотором множестве,

3) решение непрерывно зависит от входных данных.

Смысл первого условия (существование решения) состоит в том, что среди исходных данных нет противоречащих друг другу условий, исключающих возможность решения задачи. Второе условие (единственность) означает, что данных достаточно для однозначной определенности решения задачи. Третье условие (непрерывная зависимость от исходных данных) означает, что малые изменения в данных приводят к малым изменениям в решении, то есть решение устойчиво по отношению к малым возмущениям (ошибкам) данных наблюдений.

Задачи, не удовлетворяющие хотя бы одному из условий корректности, называются

В обратных задачах, как правило, отсутствует непрерывная зависимость от исходных данных в отличие от прямых задач. Математические трудности решения обратных задач связаны с тем, что обратный оператор А»1 (А — оператор в (1)) не является непрерывным. Поскольку входной информацией в обратных задачах являются экспериментальные данные, определяемые с некоторой погрешностью, которую не всегда можно оценить, то решение обратной задачи с «испорченными» входными данными может сильно отличаться от точного решения. Математически это означает, что если данные наблюдений у(/) получены с некоторой ошибкой А, то соответствующее приближенное решение

хА (^ _ А ‘ 1 [ У А 0)]

будет сколь угодно сильно отличаться от решения, соответствующего идеально точным исходным данным. Здесь хА ^), уА (^) — приближенные данные, соответственно для х^) и

у(1). В этой ситуации на первый план выходят способы математической обработки входной информации.

Отметим, что методы решения некорректных задач получили интенсивное развитие в 60-е годы XX столетия. Определяющую роль здесь сыграли работы отечественных математиков А.Н. Тихонова, М.М. Лавретньева, В.К. Иванова и др. Академиком А.Н. Тихоновым 13 и его последователями были разработаны эффективные методы решения некорректно поставленных задач — регуляризирующие алгоритмы, состоящие в сведении исходной задачи решения некоторого операторного уравнения к проблеме отыскания минимума некоторого функционала.

Некорректность присуща обратным задачам почти всегда; в одних случаях она может быть преодолена весьма просто, в других вообще требует переосмысления понятия самого решения. Рассмотрим несколько примеров.

О некоторых современных областях приложения обратных задач

Обратные задачи математической физики сформировались в основном в последние 35-40 лет, хотя первые работы относятся к 30-м годам прошлого столетия. Всё большая часть математических моделей приобретает стройность и достоверность, как раз благодаря достижениям теории обратных задач. Так, с ее помощью достигнут впечатляющий прогресс в компьютерной томографии [14]. Стремительное распространение этого метода обусловлено его эффективным применением в медицине, биологии, диагностике плазмы.

Внедрение метода компьютерной томографии произвело революцию в медицинской диагностике и электронной микроскопии биологических макромолекул. Создание компьютерных томографов (А. Кормак и Г.Н. Хаунсфилд) и их применение в биохимии (А. Клуг) отмечены Нобелевскими премиями (1979 и 1982 гг.). Отметим, что основные математические задачи вычислительной диагностики плазмы сводятся к решению операторных уравнений 1-го рода. При нахождении их приближенных решений необходимо использовать методы регуляризации, позволяющие учитывать дополнительную информацию о решении.

Первые обратные задачи были решены в связи с проблемами геофизики и разведки полезных ископаемых. В настоящее время со все большим усложнением моделей, используемых в геофизике, совершенствуется и методика решений обратных задач. Метод акустической разведки полезных ископаемых несравнимо дешевле простого бурения пробных скважин. Вместе с тем геоакустика дает возможность получать более точную информацию о состоянии недр, а звуковые волны, как известно, являются, хорошо пригодным для локации недр видом возмущения. Отметим, что в последние годы интенсивно обсуждается проект глобального вибрационного просвечивания Земли с целью уточнения ее строения.

Задачи ультразвукового неразрушающего контроля также требуют совершенствования моделей в связи с широким внедрением в практику композиционных материалов, которые обладают различными механическими свойствами по различным направлениям (анизотропией), что влечет за собой усложнение алгоритмов решения обратных задач рассеяния. Для этого класса задач очень важен учет свободной границы (для обнаружения приповерхностных дефектов) и анизотропии материала модели. Обратные задачи об определении формы дефекта приводят к последовательному решению систем интегральных уравнений 1-го рода [20] либо к решению некоторого нелинейного дифференциального уравнения [21]. В последнее время задачи, возникающие в этой области, привлекают внимание математиков-теоретиков. Это связано как с новыми постановками и новыми моделями, так и с развитием методов их решения.

Наконец, отметим, что акустическое зондирование Мирового океана является уникальным и весьма эффективным методом, поскольку радиоволны плохо распространяются в морской воде из-за ее хорошей электропроводности. Например, свет мощного лазера проникает в океанские глубины на расстояние порядка сотен метров, тогда как звук даже не очень сильного

взрыва может быть зарегистрирован на расстоянии десятков тысяч километров. Процессы, происходящие в океане, оказывают определяющее влияние на климат многих районов Земли. Кроме того, океан, мало исследованный по существу, является чрезвычайно богатым источником различных сырьевых ресурсов. Спецификой обратных задач акустики океана является достаточно сильная зашумленность полезного сигнала, а также необходимость при их решении обрабатывать огромные массивы данных.

Отметим также, что очень важную в нефтегазовой науке задачу идентификации параметров нефтегазоносного пласта можно рассматривать также и как обратную задачу теории фильтрации [23, 24].

В заключение отметим, что теория обратных задач математической физики — это бурно развивающаяся в настоящее время область современной математики, которая находит многочисленные приложения. О некоторых из них мы рассказали вкратце в настоящей заметке.

1. Лаврентьев М.М., Васильев В.Г., Романов В.Г. Многомерные обратные задачи для дифференциальных уравнений. Новосибирск, 1969. 66 с.

2. Лаврентьев М.М., Романов В.Г., I Ниигатский С.П. Некорректные задачи математической физики и анализа. М., 1980. 286 с.

3. Лаврентьев М.М., Резницкая К.Г., Яхно В.Г. Одномерные обратные задачи математической физики. Новосибирск, 1982. 88 с.

4. Романов В.Г. Обратные задачи для дифференциальных уравнений. Новосибирск, 1973. 252 с.

5. Романов В.Г. Обратные задачи математической физики. М., 1984. 264 с.

6. Белишев М.И., Благовещенский А.С. Динамические обратные задачи теории волн. СПб., 1999. 266 с.

7. Бухгейм А.Л. Введение в теорию обратных задач. Новосибирск, 1988. 181 с.

8. Кабанихин С.И. Проекционно-разностные методы определения коэффициентов гиперболических уравнений. Новосибирск, 1988. 166 с.

9. Корнилов В.С. Некоторые обратные задачи для волновых уравнений. Новосибирск, 2000. 252 с.

10. Алексеев А.С. Некоторые обратные задачи теории распространения волн // Известия АН СССР. Сер. Геофизическая. 1962. № 11. С. 1514-1531.

11. Тихонов А.Н. Об устойчивости обратных задач // Докл. АН СССР. 1943. Т. 39, № 5. С. 195-198.

12. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М., 1986. 287 с.

13. Тихонов А.Н. О решении некорректно поставленных задач и методе регуляризации // Докл. АН СССР. 1963. Т. 151, № 3. С. 501-504.

14. Тихонов А.Н., Арсенин В.Я., Тимонов А.А. Математические задачи компьютерной томографии. М., 1987. 160 с.

15. Ambarzumiyan V.A. Uber eine Frage der Eigenwerttheorie // Zeitschr. fur Phisik. 1929. Bd. 53. S. 690-695.

16. Borg G. Eine Umkehrung der Sturm-Liouvillschen Eigenwertaufgabe // Acta Math. 1946. Bd. 78, № 1. S. 196.

17. Гельфанд И.М., Левитан Б.М. Об определении дифференциального уравнения по его спектральной функции // Известия АН СССР. Сер. Математическая. 1951. Т. 15, № 4. С. 309-360.

18. Крейн М.Г. Об одном методе эффективного решения обратной краевой задачи // Докл. АН СССР. 1954. Т. 94, № 6. С. 767-770.

19. Денисов А.М. Введение в теорию обратных задач. М., 1994. 207 с.

20. Ватульян А.О., Коренский С.А. О восстановлении формы приповерхностного дефекта в полупространстве // Докл. РАН. 1995. Т. 334, № 6. С. 753-755.

21. Боев Н.В., Ватульян А.О., Сумбатян М.А. Восстановление контура препятствия по характеристикам рассеянного акустического поля в коротковолновой области // Акуст. журнал. 1997. № 4. С. 458-462.

22. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М., 1974. 332 с.

23. Георгиевский В.Б. Унифицированные алгоритмы для определения фильтрационных параметров: справочник. Киев, 1971. 328 с.

24. Мирзаджанзаде А.Х., Хасанов М.М., Бахтизин Р.Н. Моделирование процессов нефтегазодобычи. Нелинейность, неравновесность, неопределенность. М.; Ижевск, 2004. 368 с.

Видео:Пример 65. Решить задачу Коши (диффуры)Скачать

Две основные задачи динамики точки в теоретической механике

Содержание:

Две основные задачи динамики точки:

Используя дифференциальные уравнения движения материальной точки в. той или другой системе координат, можно решать две основные задачи динамики точки.

Видео:2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Первая задача

Зная массу точки и ее закон движения, можно найти действующую на точку силу. Действительно, если, например, заданы уравнения движения точки в декартовой системе координат

то проекции силы на оси координат определяются из дифференциальных уравнений движения точки (9), т. е.

Зная проекции силы на координатные оси, легко определить модуль силы и косинусы углов силы с осями координат.

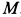
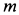
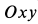
Пример 1. Точка , имеющая массу (рис. 5), движется в плоскости так, что уравнениями ее движения являются

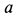
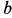
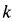
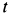
где , , — постоянные положительные величины; — время.

Определить силу, под действием которой точка совершает это движение.

Решение. Найдем уравнение траектории точки в координатной форме, исключая время из уравнений движения:

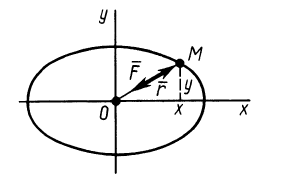
Траекторией точки является эллипс с полуосями 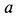и .

Рис. 5

На основании дифференциальных уравнений движения точки (10)

или, если ввести координаты движущейся точки,

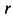
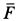
где —радиус-вектор движущейся точки. Косинусы углов силы с осями координат

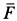
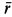
Отсюда можно заключить, что сила имеет направление, противоположное радиусу-вектору . Окончательно

Рис. 6

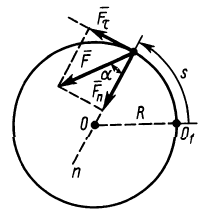
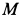
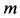
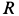
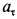
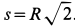
Пример 2. Точка , имеющая массу (рис. 6), движется из состояния покоя по окружности радиусом с постоянным касательным ускорением . Определить действующую на точку силу в момент, соответствующий пройденному точкой по траектории расстоянию .

Решение. Применяя дифференциальные уравнения движения точки в проекциях на естественные оси, имеем:

Так как движение происходит с постоянным касательным ускорением 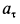без начальной скорости, то

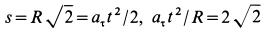
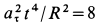
В момент, когда и, следовательно, ,

Тангенс угла 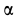между радиусом окружности и силой

Из рассмотрения первой задачи динамики точки видно, что по заданной массе точки и уравнениям ее движения сила полностью определяется как по величине, так и по направлению.

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Вторая задача

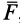
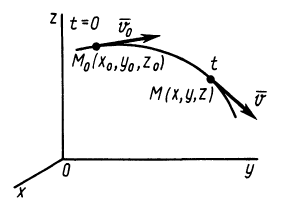
По заданной массе и действующей на точку силе необходимо определить движение этой точки. Рассмотрим решение этой задачи в прямоугольной декартовой системе координат. В общем случае сила , а следовательно, и ее проекции на координатные оси могут зависеть от времени, координат движущейся точки, ее скорости, ускорения и т. д. Для простоты ограничимся случаем зависимости силы и ее проекций на оси координат от времени, координат и скорости. Дифференциальные уравнения движения точки (9) имеют вид

Для нахождения уравнений движения точки в декартовых координатах необходимо проинтегрировать систему трех обыкновенных дифференциальных уравнений второго порядка. Из теории обыкновенных дифференциальных уравнений известно, что решение одного дифференциального уравнения второго порядка содержит две произвольные постоянные. Для случая системы трех обыкновенных дифференциальных уравнений второго порядка имеется шесть произвольных постоянных: .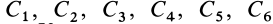

Каждая из координат 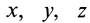движущейся точки после интегрирования системы уравнений (9) зависит от времени t и всех шести произвольных постоянных, т. е.

Если продифференцировать уравнения (13) по времени, то определяются проекции скорости точки на координатные оси:

Таким образом, задание силы не определяет конкретного движения материальной точки, а выделяет целый класс движений, характеризующийся шестью произвольными постоянными. Действующая сила определяет только ускорение движущейся точки, а скорость и положение точки на траектории могут зависеть еще от скорости, которая сообщена точке в начальный момент, и от начального положения точки. Так, например, материальная точка, двигаясь вблизи поверхности Земли под действием силы тяжести, имеет ускорение 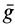, если не учитывать сопротивление воздуха. Но точка будет иметь различные скорости и положение в пространстве в один и тот же момент времени и различную форму траектории в зависимости от того, из какой точки пространства началось движение и с какой по величине и направлению начальной скоростью.

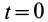
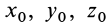
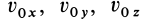
Для выделения конкретного вида движения материальной точки надо дополнительно задать условия, позволяющие определить произвольные постоянные, которых в общем случае будет шесть. В качестве таких условий обычно задают так называемые начальные условия, т.е. в какой-то определенный момент времени, например при (рис. 7), задают координаты движущейся точки и проекции ее скорости :

Рис. 7

Используя эти начальные условия и формулы (13) и (14), получаем шесть следующих уравнений для определения шести произвольных постоянных:

Если система уравнений (16) удовлетворяет условиям разрешимости, то из нее можно определить все шесть произвольных постоянных.

Начальные условия в форме (15) определяют единственное решение системы дифференциальных уравнений (9) при соблюдении соответствующих условий теории дифференциальных уравнений. Условия в других формах, как например, задание двух точек, через которые должна проходить траектория движущейся точки, могут дать или несколько решений, удовлетворяющих этих условиям, или не дать ни одного решения.

При движении точки в плоскости 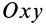имеется два дифференциальных уравнения движения. В решения этих уравнений входят четыре произвольные постоянные. Постоянные определяются из начальных условий

В случае прямолинейного движения точки имеется только одно дифференциальное уравнение и в его решение входят две произвольные постоянные. Для их определения необходимо задать начальные условия:

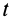
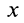
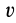
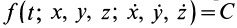
Задача интегрирования системы дифференциальных уравнений (9′) при заданных начальных условиях в общем случае является довольно трудной. Даже в простейшем случае прямолинейного движения, когда имеется только одно дифференциальное уравнение, его решение удается выразить точно в квадратурах лишь при определенной зависимости силы от времени , координаты и скорости . Поэтому важно определение таких соотношений из системы уравнений (9′), которые являются следствиями этой системы и в которые входят производные от координат точки только первого порядка. Такие соотношения, например, в виде называют первыми интегралами системы дифференциальных уравнений (9′).

Если из системы (9′) удается найти три независимых первых интеграла, то задача интегрирования упрощается, так как вместо интегрирования системы дифференциальных уравнений второго порядка достаточно проинтегрировать систему трех дифференциальных уравнений первого порядка, которую представляют эти первые интегралы.

В дальнейшем будет рассмотрен способ получения первых интегралов дифференциальных уравнений движения точки из так называемых общих теорем динамики в некоторых частных случаях движения точки.

Для выяснения особенностей решения второй основной задачи динамики, имеющей прикладное значение, рассмотрим ее решение для случая как прямолинейного, так и криволинейного движения материальной точки.

Две основные задачи динамики

Динамика имеет две основные задачи:

1. по заданному движению определить действующие силы
2. по заданным силам определить движение

Прямая и обратная задачи динамики

В динамике изучают механическое движение в связи с силами, приложенными к движущимся объектам. Следовательно, перед динамикой стоят две основные задачи:

1. по движению материального объекта (точки, твердого тела или системы точек) определить силы, производящие, данное движение. Эту задачу называют прямой, или первой основной задачей динамики;
2. вторая задача — обратная по отношению к первой, поэтому ее называют обратной, или второй основной задачей динамики: даны силы, действующие на данный материальный объект; требуется определить движение этого объекта под действием данных сил.

Наиболее просты с механической стороны эти задачи для одной материальной точки, хотя и здесь встречаются большие трудности математического характера.

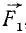
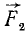
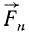
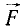
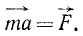
Пусть точка M массы m находится под действием сил, представленных в мгновение t векторами ,, . , или их равнодействующей . Согласно основному закону динамики ускорение, получаемое точкой M от действия сил, направлено по силе и пропорционально ей:

(123)

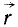
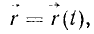
Если решают первую основную задачу динамики точки и движение точки определено в векторной форме, т. е. дан радиус-вектор как некоторая векторная функция времени t:

(54)

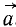
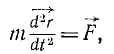
то надо определить по (57) ускорение , выражающееся второй производной от радиуса-вектора точки по времени t, и умножить его на массу т точки. Тогда мы получим следующее выражение основного закона динамики:

(125)

где правая часть даст нам искомую силу.
Если же решают вторую основную задачу динамики точки и задан вектор силы, но требуется определить радиус-вектор как функцию (54) от времени, то для решения задачи нужно интегрировать уравнение (125).

Значительно проще решать такие задачи не в векторной, а в координатной форме.

Все основные теоремы динамики точки могут быть выведены из трех дифференциальных уравнений движения материальной точки в прямоугольных координатах: mx = X; mу = Y; mz =Z

Дифференциальные уравнения движения точки в прямоугольных координатах

Пусть движение точки M задано в прямоугольных координатах кинематическими уравнениями

x = x (t), y = y (t), z = z (t). (58)

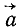
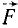
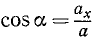
Преобразуем выражение (123) основного закона динамики; для этого определим проекции на оси координат ускорения и силы . Направляющие косинусы (67) ускорения являются вместе с тем и направляющими косинусами силы, так как направление ускорения совпадает с направлением силы. Умножая величины (123) на , получим: ma_x = F cos α.

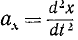
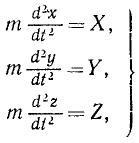
Но согласно (65) . Подставляем это значение и, пользуясь для проекции силы на ось абсцисс (и аналогично для проекций на оси у и z) знакомым нам по статике обозначением, получим

(126)

или, если обозначать вторые производные по времени двумя точками,

mx = X; mу = Y; mz =Z (126 / )

Система трех дифференциальных уравнений (126) второго порядка эквивалентна системе шести дифференциальных уравнений первого порядка:

(127)

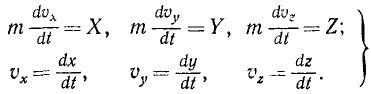
Уравнения (126) или (127) называют дифференциальными уравнениями движения материальной точки в прямоугольных координатах.

Из уравнений движения мы выведем все теоремы динамики. Они дают возможность решить и обе основные задачи динамики точки. В прямой задаче, когда кинематические уравнения движения (58) даны, решение сводится к дифференцированию этих уравнений: умножив на массу вторую производную от координаты но времени, получим проекцию силы. В обратной задаче, когда заданы проекции силы X, Y и Z, а нужно определить координаты точки х, у и z как функции времени (58), решение сводится к интегрированию трех совместных дифференциальных уравнений, где независимым переменным является время.

Три совместных дифференциальных уравнения (126) второго порядка определяют координаты х, у и z в функции времени t. Если движущаяся точка M совершенно свободна, то приложенные к ней силы могут быть функциями ее координат х, у и z, проекций ее скорости х, у и z и времени t:

Проинтегрировать их в общем виде невозможно, но при некоторых видах функции F эти интегралы могут быть получены. В очень многих случаях вычисления возможно проводить на интегрирующих машинах.

При интегрировании дифференциальных уравнений движения материальной точки появляется шесть постоянных интеграции, которые при решении каждой задачи должны быть определены из начальных условий

Постоянные интегрирования

Общие интегралы дифференциальных уравнений движения материальной точки содержат шесть постоянных интеграции: C₁, C₂, C_3, C₄, C₅, C₆. Эти постоянные величины отнюдь не являются произвольными, и в каждой частной задаче, при решении которой приходится интегрировать дифференциальные уравнения движения, постоянные интеграции должны быть определены из начальных условий. Если заданы положение и скорость движущейся точки для какого-либо мгновения t=t₀ (t₀ может быть равным или не равным нулю), то нужно определить постоянные C₁, C₂, C_3, C₄, C₅ и C₆ таким образом, чтобы при t=t₀ координаты х, у и z получили заданные значения х₀, у₀ и z₀ и производные
х, у и z — заданные значения υ_0x, υ_0y, и υ_0z.

Допускают, что данным начальным условиям соответствует только одно движение, конечно, при заданной массе m и силе F. В справедливости этого положения мы -убедимся на всех примерах, которые будем рассматривать, хотя это положение имеет и математическое доказательство. Поэтому, если мы нашли какое-либо движение точки M, удовлетворяющее уравнениям (126) и начальным данным, то, следовательно, мы определили именно то движение, которое искали.

Задача №1

Точка массы т кг движется по винтовой линии согласно кинематическим уравнениям движения: х=r cos kt, у =r sin kt, z=ut, где x, у, z и r выражены в метрах, а t — в секундах; известно, что r, k и и постоянны. Определить величину и направление силы в функции расстояния.

Решение. Задача заключается в определении силы по заданному движению, т. е. является прямой задачей динамики. Условие выражено в физической системе единиц (СИ). При решении будем выражать длину в метрах, мaccy- в килограммах и время — в секундах.

Определим по (126) проекции силы на координатные оси, для чего сначала дважды продифференцируем заданные текущие координаты точек:

х=rk 2 cos kt, у =rk 2 sin kt, z=0

Умножая на т полученные значения проекций ускорения, определим в ньютонах проекции силы:

X= — mk 2 x, Y = — mk 2 y, Z=0

Направляющие косинусы силы найдем по (6):

Ответ. Сила постоянна по величине и перпендикулярна к оси Oz.

Задача №2

Из орудия, стоящего на берегу на высоте 30 ,и над уровнем моря (рис. 160), выпущен снаряд массы m кг со скоростью 1000 м/сек под углом 30° к плоскости горизонта и под углом 60° к линии берега. Пренебрегая сопротивлением воздуха, определить точку, в которой упадет снаряд.

Решение. Единственной силой, действующей па снаряд во время полета, является его вес G = mg. Пo данной силе и по начальным данным (местоположение орудия и начальная скорость снаряда) надо определить движение снаряда и место его падения в морс. Задача относится к обратным задачам динамики. Для ее решения надо составить и проинтегрировать дифференциальные уравнения движения снаряда. Задачу будем решать в единицах СИ. Построим систему координат, взяв за начало точку О, находящуюся под орудием на уровне моря. Ось Ox направим горизонтально, перпендикулярно к берегу в сторону моря, ось Oy— вдоль берега, а ось Oz—вертикально вверх.

Для составления дифференциальных уравнений движения надо знать проекции действующей силы на оси координат. На снаряд после вылета его из орудия действовала только одна сила тяжести G = mg, направленная по вертикали вниз. Проекции действующей силы:

Дифференциальные уравнения движения снаряда напишем в виде (127):

Сокращаем на m, разделяем переменные:

откуда, интегрируя, находим:

Чтобы определить постоянные интеграции, подставим вместо t нуль, а вместо проекций скорости-их начальные значения υ_ox, υ_oy, и υ_oz, соответствующие мгновению t = 0. Получим

Таким образом, три первые постоянные интеграции в нашей задаче равны проекциям начальной скорости снаряда. Чтобы определить числовые значения этих проекций, надо знать направляющие косинусы начальной скорости. Снаряд был выпущен под углом 30° к плоскости горизонта, следовательно, угол ур> 0 начальной скорости с вертикалью равен 60°. Угол β_υ,₀, по условию задачи, тоже равен 60 o , cos _υ,₀ определим из равенства единице Суммы квадратов направляющих косинусов:

Теперь нетрудно определить и проекции начальной скорости:

Мы получили числовые значения постоянных интеграции:

Подставляя эти значения постоянных в уравнения и выражая проекции скоростей по (63), получим три новых дифференциальных уравнения:

Разделив переменные и проинтегрировав, получим

Для определения C₄, C₅ и C₆ подставим и в эти уравнения вместо t его частное значение 0, а вместо х, у и z —их частные значения x₀, у₀ и z₀:

При выбранной нами системе координат имеем x₀ =0; y_{0 =} 0; z₀ = + 30м, следовательно, C₄ = 0; C₅=0; C₆=+30.
Подставляя эти значения в уравнения, полученные после второго интегрирования, найдем кинематические уравнения движения снаряда:

Чтобы определить положение точки, в которой снаряд упадет в море, надо знать продолжительность полета снаряда. Для этого приравняем нулю аппликату z, так как в мгновение, когда снаряд коснется моря, он будет находиться в плоскости хОу. Из уравнения

4,905t 2 — 500t-30 = 0

находим два значения: t=101,6 сек и t=—0,06 сек. Второе значение отбрасываем а первое подставляем в кинематические уравнения движения. Находим ответ.
Ответ. x = 71 831 м — 71,8 км; у = 50 800 м — 50,8 км; z = 0.

Из этого примера видно, что движение точки зависит не только от действующих сил, но и от начальных данных. Если бы начальная скорость или начальные координаты были иными, то и движение снаряда отличалось бы от полученного. Оно по-прежнему было бы равномерным но горизонтали и равнопеременным по вертикали; траекторией снаряда оставалась бы парабола, но она была бы иной и иначе расположенной; иной была бы и точка попадания. Полученные значения постоянных C₁, C₂, . C₆ определены для данной задачи, и при этих значениях постоянных может быть только одно найденное нами решение. Эти постоянные величины вовсе не являются произвольными. Постоянные интеграции, являясь первоначальными значениями переменных, придают решению какой-либо задачи механики всю ту общность, какую она способна иметь.

Вариации постоянных интеграции. Пусть движение какой-либо точки M массы m происходит под действием силы 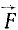. Составив и проинтегрировав дифференциальные уравнения движения точки, определим постоянные интеграции C₁, C₂, . C₆. Тогда, подставляя в полученные уравнения частные значения времени t, мы можем определить положение точки M во всякое данное мгновение. Пусть, например, в мгновение t₁ координаты точки M равны x₁, y₁, z₁. Если мы дадим постоянным интеграции бесконечно малые приращения δC₁, δC₂, . произвольного знака и произвольной величины, называемые вариациями, то положение точки M в то же мгновение t₁, но при измененных постоянных интеграции C₁ + δC₁, C₂ + δC₂, . будет иным. Точка M при неизменившемся времени получит бесконечно малое отклонение, координаты ее получат некоторые бесконечно малые приращения δx₁, δy₁, δz₁, называемые вариациями координат точки, при движении, определяемом величинами C₁, C₂, . постоянных интеграции.

Задача №3

Движение точки весом 2 Г выражается уравнениями x= 3cos2πt см; y=4sinπt см, где t выражено в секундах. Определить проекции силы, действующей на точку, в зависимости от ее координат.

Решение. Задача относится к прямым задачам динамики: по данному движению точки надо определить действующую силу. Для ее решения продифференцируем дважды кинематические уравнения движения точки и, умножив на m найденные х и у, получим X и Y.

Условие дано в технической системе единиц, и в этой задаче примем L в см, F в Г и T сек. Кинематические уравнения движения известны. Дифференцируя дважды, находим

х — 4π 2 3 cos 2πt = — 4π 2 x;
у = —4π 2 sin πt = — π 2 у.

Умножая массу 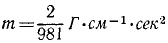на проекции ускорения, найдем проекции силы в граммах. Чтсбы перевести их в ньютоны, надо умножить число граммов на 0,00981.

Решим теперь эту же задачу в физической системе единиц. Принимать за основные единицы метр, килограмм и секунду в этой задаче нецелесообразно. Выразим L в см, M в г и T в сек.

В условии задачи дан вес точки G = 2 Г. Следовательно, ее масса m = 2 г. Умножая проекции ускорения на массу, выраженную в граммах, получим проекции силы в динах:

X = — 8π 2 x = — 78,88x [дин];
Y = — 2π 2 y = — 19,72y [дин].

Чтобы выразить их в ньютонах, надо число дин поделить на 100000.

Ответ. X =— 0,08χ Г = —78,88x дин = —0.0007888x н;
Y = —0,02x Г =— 19,72y дин = —0,0001972y н.

Обратим внимание на одно обстоятельство, которое легко усмотреть в только что решенной задаче. Определяя силу по заданному движению материальной точки, мы нашли, что движение произведено силой, являющейся функцией координат точки. Но мы могли бы выразить силу и как функцию времени. В самом деле, продифференцировав дважды кинематические уравнения движения и умножив вторые производные на m, найдем

X = — 12rnπ 2 cos 2πt; Y = —4rnπ 2 sin πt.

Так одно и то же движение может совершаться под действием различно выраженной силы.

Из этого же примера видно, что если точка движется в одной плоскости, то, приняв эту плоскость за плоскость хОу, можно описать движение точки системой первых двух дифференциальных уравнений движения (126′); третье же дифференциальное уравнение становится лишним.

Задача №4

Найти плоскую траекторию точки M массы m, притягиваемой к неподвижному центру О с силой, пропорциональной расстоянию r и равной k 2 mr, при следующих начальных данных:

Решение. Задача относится к обратным задачам динамики: по заданной силе определить движение. Точка M описывает плоскую траекторию, и нам понадобятся только два уравнения движения.

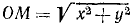
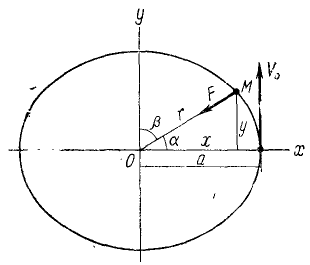
Если в какое-либо мгновение t точка M имела координаты х и у и находилась от центра на расстоянии (рис. 161), то проекции силы на оси координат:

Рис. 161

Дифференциальными уравнениями движения точки являются:

Сократим на т и умножим первое из уравнений на υ_xdt=dx, а второе—на υ_ydt = dy:

Интегрируем и умножаем на 2:

Для определения постоянных интеграции C₁ и C₂ подставляем в эти уравнения вместо переменных величин их начальные значения:

Значения постоянных вносим в уравнения, одновременно выражая υx и υy по (63):

Извлекаем квадратные корни, разделяем переменные н интегрируем:

Для определения постоянных интеграции C₃ и C₄ подставляем в эти уравнения вместо переменных величин t, х и у их начальные значения:

Эти значения постоянных интеграции вносим в уравнения:

Мы получили кинематические уравнения движения (58) точки в декартовых координатах. Чтобы определить траекторию, надо из них исключить время. Возводя в квадрат и складывая, получаем уравнение траектории

Ответ. Эллипс с полуосями a и .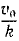

В еще более частном случае, когда сила имеет постоянное направление, а начальная скорость направлена по силе или равна нулю, движение точки прямолинейно. Направив ось Ox по этой траектории, мы обойдемся первым из уравнений (126), которое и нужно интегрировать, чтобы получить закон (58 , ) искомого движения точки. При этом нельзя забывать, что под X мы понимаем не силу, а ее проекцию F cos a, которая в данном случае по величине равна модулю силы. Если α = 0, то сила направлена в сторону положительной оси Ох, и тогда Х>0. Если же α = π, то сила направлена в сторону отрицательного направления оси Ох, тогда X 2 υ 2 .

Решение. Предположим, что тело начинает падать из начального положения О, и направим вниз из точки О ось Ох. Так как движение прямолинейное, то для его определения достаточно первого уравнения (126). На падающее тело действуют две силы: 1) постоянная сила G = mg, направленная в положительную сторону оси Ох, и 2) переменная сила R = mgk 2 υ 2 , являющаяся функцией скорости; она возрастает пропорционально квадрату скорости и направлена против скорости, а следовательно, против положительного направления оси Ох. Имеем

Перепишем это уравнение, сократив его на m:

Из этого уравнения видно, что падение не может быть равноускоренным, что по мере возрастания скорости сила сопротивления увеличивается, правая часть уравнения уменьшается и ускорение стремится к нулю.

Чтобы взять интеграл, перемножим соответственно левые и правые части этого уравнения и следующего выражения:

Это уравнение позволяет определить скорость падающего тела во всякое данное мгновение t. Оно уточняет известную формулу υ=gt, так как здесь учтено и сопротивление воздуха.

Ответ.

Движение точки можно описать в проекциях на оси естественного трехгранника двумя уравнениями:

Дифференциальные уравнения движения материальной точки в форме Эйлера. В кинематике мы изучали три способа определения движения точки: 1) векторный, 2) в прямоугольных координатах, 3) естественный. Соответственно и в динамике мы можем определить движение точки по заданным силам (или силы по заданному движению) векторным уравнением (125), в проекциях на прямоугольные оси — уравнениями (126), а также естественными уравнениями движения. Из многих форм уравнений движения эти три применяют наиболее часто.

Проецируя ускорение на оси естественного трехгранника, мы нашли (см. § 23), что проекции ускорения на касательную а_N, на главную нормаль αv и на бинормаль a_b выражаются следующими формулами:

и вместо трех составляющих полное ускорение имеет только две. Но сила всегда направлена по ускорению точки, а следовательно, проецируя силу на оси естественного трехгранника, мы и здесь получим только две составляющие (F_T — на касательную и F_N— на главную нормаль) и определим движение точки только двумя уравнениями:
(128)

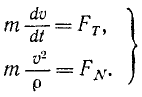
Задача №6

Горнолыжник в конце склона развил скорость 54 км/ч, после чего свободно скользил по горизонтальному прямолинейному участку пути. Определить длину и время свободного скольжения, если коэффициент трения лыж по снегу f’ = 0,051.

Решение. В задаче примем единицы СИ; тогда вес лыжника, выраженный в ньютонах, G = 9,81 ∙m, где m — его .масса в кг. Задача является обратной задачей динамики, так как требуется определить движение по заданной силе F_гp— f’G. Достаточно одного первого из уравнений (128), потому что движение прямолинейное. Проекция силы имеет отрицательный знак, так как сила трения направлена против скорости, а скорость направлена в положительном направлении (в сторону возрастания расстояния): .

Сокращаем на m и разделяем переменные:

Чтобы определить постоянную C₁, подставим вместо t нуль, а вместо υ—начальное значение скорости —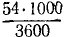= 15 м/сек:

Подставляя это значение C₁ в уравнение, полученное после интегрирования, и заменяя υ по (53), получим новое дифференциальное уравнение:

Разделим переменные и проинтегрируем:

В начальное мгновение лыжник не прошел еще никакого расстояния по горизонтальному участку, а потому C₂ = 0. Время скольжения до остановки определим, положив в уравнении, полученном для скорости,

15 — 0,50t=0, откуда t = 30.

Подставляя это значение t в последнее уравнение, найдем длину свободного скольжения.

Ответ. Время скольжения 30 сек, длина 225 м.

Задача №7

Маятник Борда для определения ускорения свободно падающих тел представляет собой латунный шарик массой 200 г, подвешенный на очень тонкой проволоке длиной 100 см. При качании шарик в наинизшем положении имеет скорость 8 см/сек. Определить натяжение проволоки в ее нижнем конце при наинизшем положении маятника.

Решение. В задаче применена физическая система единиц. Примем L в см, M в г, T в сек.

Задача относится к прямым задачам динамики. Чтобы по данному движению латунного шарика, принимаемого за материальную точку, определить действующую силу, напишем второе из естественных уравнений движения материальной точки (128). В наинизшем положении на шарик действует сила натяжения проволоки, проекцию которой T будем считать положительной, так как она направлена внутрь траектории, и сила тяжести G = 200 . 981 дин, проекцию которой будем считать отрицательной:

или, подставляя числовые значения,

откуда получаем ответ.
Ответ. T = 196 328 дин = 1,96328 н.

Движение точки в плоскости можно описать двумя уравнениями в полярных координатах.

Уравнения движения точки в полярных координатах

В ряде задач бывает удобно исследовать движение точки в полярных координатах. Примем без доказательства, что проекция ускорения точки на полярный радиус-вектор равна (r — rφ 2 ), а на перпендикулярное направление равна (rφ + 2rφ). Помножив на массу эти проекции ускорения точки и приравняв проекциям силы, напишем дифференциальные уравнения движения точки в полярных координатах:

(129)

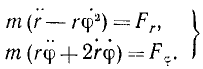
где m_k—масса k-й точки, x_k, y_k и z_k-проекции ее ускорения, a X_k, Y_k и Z_k—проекции равнодействующей всех сил, приложенных к этой точке (k = 1, 2, 3, . n).

Далеко не всегда действующие силы бывают известны. Обычно остаются неизвестными внутренние силы. Для вывода некоторых общих теорем динамики и при решении некоторых частных задач бывает удобным выделить внутренние силы уже при написании дифференциальных уравнений движения.

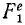
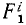
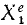
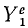
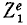
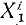
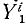
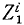
Рассмотрим сначала одну из материальных точек системы, например точку с индексом 1 <k= 1), и распределим все силы, приложенные к этой точке, на две группы: внешние и внутренние. Сложив все внешние силы, действующие на эту точку, получим их равнодействующую , а сложив все внутренние, получим равнодействующую внутренних сил . Проекции этих сил обозначим ,, и ,, .

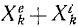
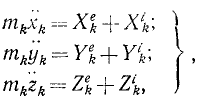
Аналогично поступим с силами, приложенными к остальным точкам, и заменим в написанных выше уравнениях проекции равнодействующей X_k суммой , то же сделаем по двум другим осям. Тогда дифференциальные уравнения примут вид:

(130)

Следовательно, движение свободной механической системы, состоящей из n материальных точек, определяется системой 3n дифференциальных уравнений второго порядка.

Если система не свободна, а на нее наложены связи, выражающие некоторую зависимость между координатами точек механической системы, то бывает возможным сократить число дифференциальных уравнений движения, о чем будет подробнее сказано в § 52 и § 53.

В ряде случаев оказывается целесообразным разделить все силы, действующие на материальные точки механической системы на две категории по иному признаку, а именно на активные силы и реакции связей. Как уже было сказано, реакции связей часто зависят от движения системы и не могут быть найдены, пока не определено движение системы. 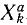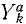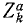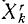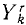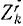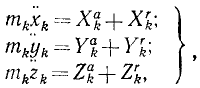Обозначая проекции равнодействующей всех активных сил, действующих на k-ю точку, , и , а проекции равнодействующей всех реакций связей, приложенных к k-й точке, , и , получим:

(130′)

Во всем вашем курсе (если это специально не оговорено) рассмотрены только свободные механические системы и механические системы с идеальными связями. Понятие идеальных связей нам уже встречалось в статике (см. § 4) и будет уточнено в динамике (см. § 51).

В дальнейшем из дифференциальных уравнений (130) и (130′) мы выведем общие теоремы динамики таких материальных систем.

Решение многих проблем по динамике механических систем сопряжено с большими трудностями математического характера. Интегрирующие машины в очень многих случаях дают возможность преодолеть эти трудности.

• Прямолинейное движение точки
• Криволинейное движение материальной точки
• Движение несвободной материальной точки
• Относительное движение материальной точки
• Сложение движение твердого тела
• Кинематика сплошной среды
• Аксиомы классической механики
• Дифференциальные уравнения движения материальной точки

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

💥 Видео

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Дифференциальные уравнения. 11 класс.Скачать

Математика это не ИсламСкачать

Операционное исчисление. Решить неоднородное дифференциальное уравнение 2 порядкаСкачать

Задачи приводящие к дифференциальным уравнениям.Скачать

Задача Коши для дифференциальных уравненийСкачать

Частное решение дифференциального уравнения. 11 класс.Скачать

Дифференциальные уравнения | задача Штурма - Лиувилля | классические краевые задачи | 1Скачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать