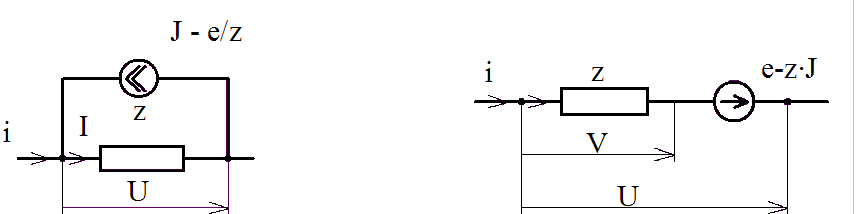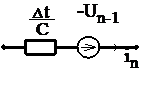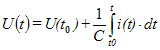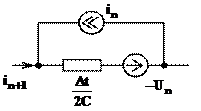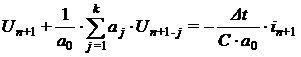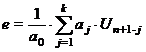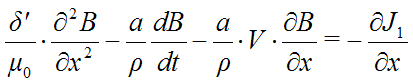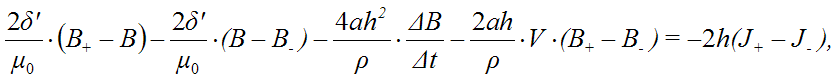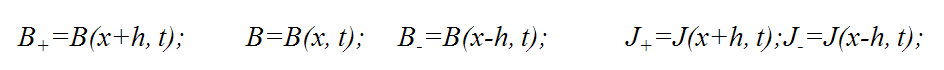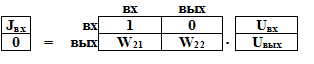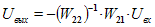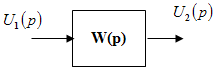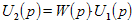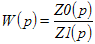Обобщенные ветви и их уравнения в формах z и y матричные уравнения для обобщенных ветвей (6 видео)

Содержание

Обобщенные ветви и их уравнения в формах z и y матричные уравнения для обобщенных ветвей
Обобщенные ветви и их уравнения в формах z и y матричные уравнения для обобщенных ветвей
Формирование уравнений электрической цепи
📺 Видео

Видео:Решение матричных уравненийСкачать

Обобщенные ветви и их уравнения в формах z и y матричные уравнения для обобщенных ветвей

Здесь приводится краткая информация об обобщенной ветви и способах представления в форме обобщенной ветви различных численных методов. Более подробно авторский материал изложен в книге «Вычислительные модели и алгоритмы тензорного анализа сетей». в разделах 2.1. «Обобщенная ветвь» и 3.1.»Резистивная схема замещения разностного уравнения».

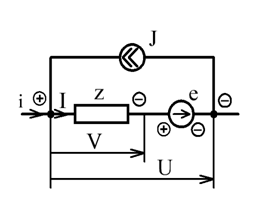
Обобщенная ветвь представлена на следующем рисунке:

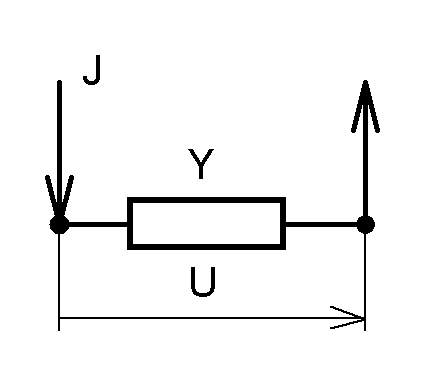
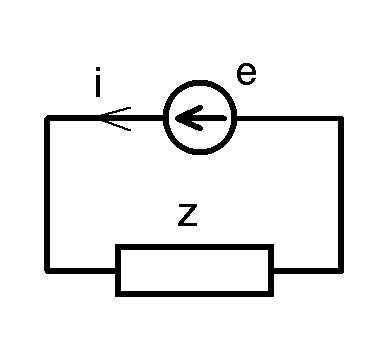
U — напряжение на узлах ветви, e — источник напряжения ветви, z — сопротивление ветви,

Y — проводимость ветви, i — ток, J — источник тока ветви.
Напряжение на внешних узлах ветви U равно разности между напряжением V на сопротивлении и электродвижущей силой е:

Ток в ветви I равен сумме тока источника J и тока i , проходящего через ветвь:

Закон Ома для сопротивления z :

V = z · I ,

Последнее равенство выразим через ток i и напряжение U :

U + e = z ·( i + J ).

Полученное уравнение есть уравнение обобщенной ветви, приведенной на выше рисунке.

Обобщенную ветвь можно представить в двух эквивалентных формах, приведенных ниже:

U = z ·( i + J э), где J э = ( J — e / z )

U + e _э = z · i , где e _э= e – z · J

Кроме обобщенной ветви, применяются так называемые примитивные ветви. Для анализа схем по методу узловых напряжений в качестве примитивной ветви используется узловая ветвь, для анализа схем по методу контурных токов используется контурная ветвь:

узловая примитивная ветвь J = Y · U

контурная примитивная ветвь e = z · i

Независимые источники, как правило, не представляют собой отдельную ветвь. Они предназначены в первую очередь для представления топологии схемы — узловых пар и контуров. Поэтому изображение на схеме, например, идеального источника тока будет означать то, что на данной координате задан ток узловой пары.

На обобщенной ветви можно построить электрические модели разностных схем для дифференциальных уравнений двухполюсников. Например, линейную емкость, представленную дифференциальным уравнением: i = C dU/dt

можно представить в форме обобщенной ветви — контурной или узловой для неявного метода Эйлера 1-го порядка:

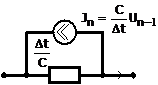
узловая форма

Аналогичным образом можно построить разностные электрические схемы замещения для любых численных методов.

Например, если связь между током и напряжением представлена интегральным уравнением:

То разностная схема замещения емкости для метода трапеций выглядит так:

Для многошагового метода обратного дифференцирования, разностная схема замещения дифференциального уравнения емкости:

может быть представлена обобщенной ветвью U + e = z ∙ i, где

Нелинейные двухполюсники представляются разностно-итерационными схемами замещения.

Если в дифференциальном уравнении нелинейной емкости: i_c = dQ/dt, емкость зависит от напряжения: Q =C(Uc) ∙ Uc, то можно получить следующую разностно-итерационную схему замещения двухполюсника с нелинейной емкостью:

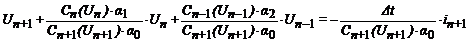
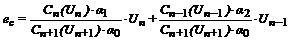
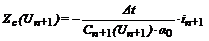
Значение емкости на n+1 шаге уточняется прямыми итерациями.

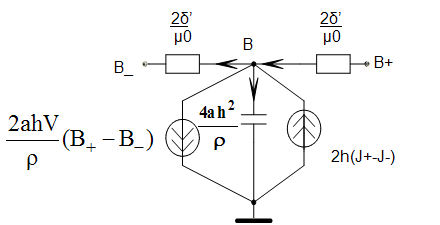
Проиллюстрируем применение обобщенной ветви для построения электрических схем замещения дифференциальных уравнений с частными производными.

Пусть имеется дифференциальное уравнение для распределения магнитной индукции В вдоль оси х:

Выполняя аппроксимацию центральными разностями, получаем следующее разностное уравнение:

Полагая, что каждое слагаемое моделируется током некоторой схемы замещения, получаем, что индукция ссответствует потенциалам этой схемы:

Электрическая схема замещения приведенного уравнения с частными производными будет следующей:

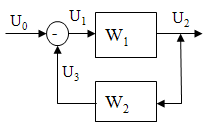
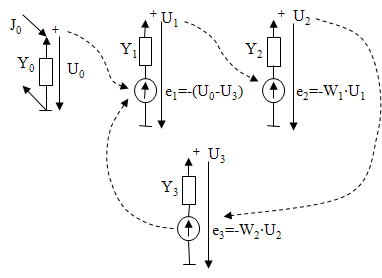
Рассмотрим теперь электрические модели сигнальных подсистем. В качестве иллюстрации приведем схему с обратной связью:

Считая, что каждый сигнал на входе и входе моделируется напряжением, а связь между выходом и входом заменена источником напряжения, управляемым напряжением, получаем следующую схему замещения:

В этой схеме можно принять проводимости ветвей единичными, так как токи в схеме отсутствуют (за исключением входных цепей, где тоже можно принять без ущерба для расчетов единичные проводимости). Тогда система уравнений сведется к следующему блочно-матричному виду:

Первое строка имеет тривиальное решение, а вторая строка связывает выходные сигналы с входными:

В этом уравнении блок W 22 известен в теории регулирования как структурная матрица.

Отдельные блоки аналоговых систем управления представляются передаточными функциями:

Здесь выходной сигнал и входной связаны уравнением:

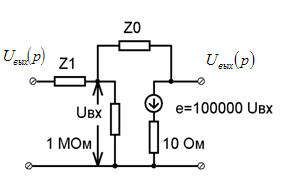
Передаточную функцию W можно смоделировать схемой на операционном усилителе, если отношение сопротивления Z0 в обратной связи операционного усилителя к его входному сопротивлению Z1 равно этой передаточной функции:

В свою очередь сам операционный усилитель в простейшем случае моделируется управляемым источником напряжения. В этом случае простейшей схемной моделью на операционном усилителе звена, заданного передаточной функцией будет следующая

Схемы замещения на операционных усилителях могут моделировать нелинейные передаточные звенья.

Видео:Лекция 8. Решение матричных уравненийСкачать

Обобщенные ветви и их уравнения в формах z и y матричные уравнения для обобщенных ветвей

Рассмотренные методы расчета электрических цепей – непосредственно по законам Кирхгофа, методы контурных токов и узловых потенциалов – позволяют принципиально рассчитать любую схему. Однако их применение без использования введенных ранее топологических матриц рационально для относительно простых схем. Использование матричных методов расчета позволяет формализовать процесс составления уравнений электромагнитного баланса цепи, а также упорядочить ввод данных в ЭВМ, что особенно существенно при расчете сложных разветвленных схем.

Переходя к матричным методам расчета цепей, запишем закон Ома в матричной форме.

Пусть имеем схему по рис. 1, где — источник тока. В соответствии с рассмотренным нами ранее законом Ома для участка цепи с ЭДС для данной схемы можно записать:

(1)

Однако, для дальнейших выкладок будет удобнее представить ток как сумму токов k -й ветви и источника тока, т.е.:

(2)

Подставив (2) в (1), получим:

(3)

Формула (3) представляет собой аналитическое выражение закона Ома для участка цепи с источниками ЭДС и тока (обобщенной ветви).

Соотношение (3) запишем для всех n ветвей схемы в виде матричного равенства

(4)

где Z – диагональная квадратная (размерностью матрица сопротивлений ветвей, все элементы которой (взаимную индуктивность не учитываем), за исключением элементов главной диагонали, равны нулю.

Соотношение (4) представляет собой матричную запись закона Ома.

Если обе части равенства (4) умножить слева на контурную матрицу В и учесть второй закон Кирхгофа, согласно которому

(5)

(6)

то есть получили новую запись в матричной форме второго закона Кирхгофа.

Метод контурных токов в матричной форме

В соответствии с введенным ранее понятием матрицы главных контуров В , записываемой для главных контуров, в качестве независимых переменных примем токи ветвей связи, которые и будут равны искомым контурным токам.

Уравнения с контурными токами получаются на основании второго закона Кирхгофа; их число равно числу независимых уравнений, составляемых для контуров, т.е. числу ветвей связи c = n — m +1 . Выражение (6) запишем следующим образом:

(7)

В соответствии с методов контурных токов токи всех ветвей могут быть выражены как линейные комбинации контурных токов или в рассматриваемом случае токов ветвей связи. Если элементы j –го столбца матрицы В умножить соответствующим образом на контурные токи, то сумма таких произведений и будет выражением тока j –й ветви через контурные токи (через токи ветвей связи). Сказанное может быть записано в виде матричного соотношения

(8)

где — столбцовая матрица контурных токов; — транспонированная контурная матрица.

С учетом (8) соотношение (7) можно записать, как:

(9)

Полученное уравнение представляет собой контурные уравнения в матричной форме. Если обозначить

(10)

(11)

то получим матричную форму записи уравнений, составленных по методу контурных токов:

(12)

где — матрица контурных сопротивлений; — матрица контурных ЭДС.

В развернутой форме (12) можно записать, как:

(13)

то есть получили известный из метода контурных токов результат.

Рассмотрим пример составления контурных уравнений.

Пусть имеем схему по рис. 2. Данная схема имеет четыре узла ( m =4) и шесть обобщенных ветвей ( n =6). Число независимых контуров, равное числу ветвей связи,

Граф схемы с выбранным деревом (ветви 1, 2, 3) имеет вид по рис. 3.

Запишем матрицу контуров, которая будет являться матрицей главных контуров, поскольку каждая ветвь связи входит только в один контур. Принимая за направление обхода контуров направления ветвей связи, получим:

Диагональная матрица сопротивлений ветвей

Матрица контурных сопротивлений

Z_k=BZB T

Матрицы ЭДС и токов источников

Тогда матрица контурных ЭДС

Матрица контурных токов

Таким образом, окончательно получаем:

где ; ; ; ; ; ; ; ; .

Анализ результатов показывает, что полученные три уравнения идентичны тем, которые можно записать непосредственно из рассмотрения схемы по известным правилам составления уравнений по методу контурных токов.

Метод узловых потенциалов в матричной форме

На основании полученного выше соотношения (4), представляющего собой, как было указано, матричную запись закона Ома, запишем матричное выражение:

(14)

где — диагональная матрица проводимостей ветвей, все члены которой, за исключением элементов главной диагонали, равны нулю.

Умножив обе части равенства (14) на узловую матрицу А и учитывая первый закон Кирхгофа, согласно которому

(15)

(16)

Выражение (16) перепишем, как:

(17)

Принимая потенциал узла, для которого отсутствует строка в матрице А , равным нулю, определим напряжения на зажимах ветвей:

(18)

Тогда получаем матричное уравнение вида:

(19)

Данное уравнение представляет собой узловые уравнения в матричной форме. Если обозначить

(20)

(21)

то получим матричную форму записи уравнений, составленных по методу узловых потенциалов:

(22)

где — матрица узловых проводимостей; — матрица узловых токов.

В развернутом виде соотношение (22) можно записать, как:

(23)

то есть получили известный из метода узловых потенциалов результат.

Рассмотрим составление узловых уравнений на примере схемы по рис. 4.

Данная схема имеет 3 узла ( m =3) и 5 ветвей ( n =5) . Граф схемы с выбранной ориентацией ветвей представлен на рис. 5.

Диагональная матрица проводимостей ветвей:

где .

Матрица узловых проводимостей

Матрицы токов и ЭДС источников

Обобщенные ветви и их уравнения в формах z и y матричные уравнения для обобщенных ветвей

Следовательно, матрица узловых токов будет иметь вид:

Таким образом, окончательно получаем:

где ; ; ; ; .

Анализ результатов показывает, что полученные уравнения идентичны тем, которые можно записать непосредственно из рассмотрения схемы по известным правилам составления уравнений по методу узловых потенциалов.

Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

В чем заключаются преимущества использования матричных методов расчета цепей?
Запишите выражения матрицы контурных сопротивлений и матрицы контурных ЭДС.
Запишите выражения матрицы узловых проводимостей и матрицы узловых токов.
Составить узловые уравнения для цепи на рис. 2.

Составить контурные уравнения для цепи рис. 4, приняв, что дерево образовано ветвями 3 и 4 (см. рис. 5).

Видео:Матричные уравнения Полный разбор трех типов матричных уравненийСкачать

Формирование уравнений электрической цепи

Подходы к формированию уравнений электрических цепей и способы их решения рассмотрим с помощью схем с резистивными элементами и источниками постоянных напряжений и токов. Это не снижает общности методов, но в то же время позволяет на примерах алгебраических уравнений проанализировать достоинства и недостатки отдельных способов.

Рассмотрим резистивную схему, п_у узлов и и_в ветвей, которую можно однозначно характеризовать значениями 2п_и переменных, представляющих собой токи и напряжения всех ветвей. Уравнения схемы формируют на основе соотношений между токами и напряжениями и_в ветвей (компонентные) и правил Кирхгофа (топологические). По правилу Кирхгофа для токов можно составить (Пу — 1) независимых уравнений для узлов схемы

причем для одного из узлов, называемого базисным, уравнение представляет собой сумму токов всех других узлов. Таким образом, для получения полной системы уравнений по правилу Кирхгофа для напряжений следует сформировать (п_в — п_у +1) независимых уравнений вида

Выбор контуров, обеспечивающих независимость полученных уравнений, можно осуществить, например, таким образом, чтобы в каждый контур входила по крайней мере одна новая ветвь. В случае планарных схем, которые могут быть изображены на плоскости без пересечений, независимые контуры можно выбрать по ячейкам эквивалентной схемы. Для наглядности выявления ячеек и узлов удобно от схемы перейти к графу (скелету) цепи.

Топологический граф представляет собой совокупность ребер (направленных отрезков линий), соответствующих ветвям схемы, и вершин, соответствующих узлам схемы, т.е. точкам соединения двух и более ветвей. Направления ветвей графа совпадают с положительными согласованными направлениями тока и напряжения ветви. Для упрощения структуры графа сложных схем вводят понятие обобщенной ветви, содержащей набор возможных компонентов (рис. 2.13, а).

Обобщенная ветвь описывается зависимостью напряжения от тока

В качестве примера построим топологический граф для схемы, содержащей п_у = 3 узла и п_в = 4 ветви (рис. 2.13, б). С использованием обобщенных ветвей получим структуру графа (рис. 2.13, в). С помощью графа запишем топологические уравнения токов:

Рис. 2.13. Обобщенная ветвь (я), резистивная схема (б) и ее граф (в)

Выбрав контуры в форме ячеек графа, получим уравнения для напряжений:

Компонентные уравнения обобщенных ветвей имеют вид

Полученная система содержит восемь уравнений с неизвестными 1 /₂; /₃; hU t/₂; Z7₃; f/₄. Количество неизвестных можно сократить вдвое, подставив компонентные соотношения в уравнения для напряжений.

Способы упрощения расчета линейных электрических схем основаны на их свойствах. К наиболее употребительным следует отнести метод суперпозиции (наложения), который позволяет представить токи и напряжения в схеме с несколькими источниками алгебраической суммой составляющих, обусловленных действием каждого источника V/ и J_a

Коэффициенты g/_;, Kj_q, Кф ?)_](<, называемые функциями передачи цепи, могут быть вычислены или определены экспериментально при соответствующем режиме, например коэффициент передачи напряжения К/у = Ufj/Vj при J_q = 0; Vj*_q = 0.

Часто в схеме требуется вычислить ток одной ветви (например, в нагрузке). Для этого применяется метод эквивалентного генератора, состоящий в замене схемы относительно рассматриваемой ветви активным двухполюсником (рис. 2.14, а).

Активный двухполюсник можно представить одной из схем эквивалентного источника: последовательной (рис. 2.14, б), описываемой выражением Uj = U_p — r_liTIj, или параллельной (рис. 2.14, в), для которых справедливо выражение Ij = I_K— g_m Uj.

Рис. 2.14. Эквивалентный источник (а) и его схемы: последовательная (б); параллельная (в)

Параметры эквивалентного источника: U_p — напряжение на разомкнутых зажимах (/, = 0); 1_К — ток при замкнутых зажимах источника ( Uj = 0); г_вт и g_BT — внутреннее сопротивление и проводимость относительно рассматриваемой ветви исходной схемы с исключенными источниками. При этом для эквивалентности должны выполняться равенства /_к = g_BTJ7_p и g_BT = 1 /г_вт.

Важнейшим условием при анализе изолированной электрической цепи (не связанной с другими устройствами), является обеспечение энергетического баланса, т.е. нулевого значения суммарной мощности ветвей схемы

При вычислении баланса мощностей его удобно записать раздельно для приемников и источников:

Причем мощности источников должны быть записаны с соответствующими знаками в зависимости от направлений токов и напряжений. Так, для приведенной линейной схемы баланс мощностей имеет вид

Обычно при расчетах электрических цепей баланс мощностей составляют для контроля правильности результатов.

При сложной конфигурации цепи выбор контуров, дающих возможность сформировать систему независимых уравнений, становится достаточно сложной задачей, решение которой базируется на применении топологических графов и отображающих их матриц: узловой А, описывающей присоединение ветвей к узлам схемы, и контурной В, отражающей образование контуров из ветвей. Несложно выработать достаточно очевидные алгоритмы формирования соответствующих матриц. Так, например, для представленного графа линейной резистивной схемы матрицы имеют вид

Если токи и напряжения ветвей схемы представить в форме столбцовых матриц Р = [Д, /₂, /3, /₄] 1 и u B = [ U, U₂, U_?>, t/₄] T , то уравнения Кирхгофа можно записать в матричном виде:

Для получения системы независимых уравнений применяются разработанные в теории графов методы формирования соответствующих матриц главных сечений и главных контуров. Недостатками полной системы уравнений электрической схемы, составленной на основе уравнений Кирхгофа, наряду с большой размерностью является отсутствие регулярности в их структуре.

С целью уменьшения числа совместно решаемых уравнений в электротехнике широко применяются методы замены переменных, которые снижают размерность системы и позволяют с помощью полученных значений новых переменных определить все токи и напряжения схемы.

Наибольшее распространение при расчете сложных схем получил метод узловых напряжений (потенциалов), в котором в качестве независимых (искомых) переменных выбраны напряжения узлов схемы относительно базисного узла (потенциалы узлов). Метод приводит к минимальному числу совместно решаемых уравнений, так как для большинства схем число узлов меньше числа ветвей.

Общий подход формирования узловых уравнений состоит в записи напряжений ветвей через разность потенциалов их узлов и подстановку в уравнения для токов узлов. В результате образуется система линейных алгебраических уравнений с (п_у — 1) неиз- вестными потенциалами узлов. Так, для рассматриваемой схемы выражения напряжений ветвей через потенциалы узлов имеют вид

Их подстановка в соотношения для токов приводит к системе уравнений

Узловые уравнения принято представлять в обобщенной форме:

В приведенной системе приняты обозначения: g_yy — собственные узловые проводимости, равные сумме проводимостей ветвей, подключенных к узлу; g_yj — взаимные проводимости между узлами / и у, равные сумме проводимостей ветвей, соединяющих узлы; Л’ — узловые токи, равные сумме источников тока и эквивалентных им источников напряжения, подключенных к узлу, причем со знаком «плюс» записывают токи, направленные к узлу (входящие).

Запись узлового преобразования в матричной форме u B = A ! cp приводит к следующей матричной записи узловых уравнений:

Общая форма записи узловых уравнений обладает регулярной структурой, которая позволяет формировать их посредством последовательного суммирования вкладов отдельных элементов схемы. Это свойство дает возможность автоматического получения матрицы в компьютере с осуществлением контроля полученного результата. После решения этой системы (расчета потенциалов узлов) можно вычислить напряжения и токи ветвей.

В электрических и электронных устройствах широкое применение имеютмногополюсные элементы, присоединяемые костальной части схемы более чем двумя проводниками. Наиболее распространенными элементами являются четырехполюсные, имеющие две пары зажимов для присоединения к остальной части цепи, например между источником сигнала и приемником (рис. 2.15, а).

антов записи компонентных уравнений: |А Наиболее часто используются формы ||Z||, | выражаются следующими зависимостями:

Рис. 2.15. Четырехполюсник (Ч) с источником и нагрузкой (а), его топологический граф (б)

При составлении уравнений схем с двухполюсными и четырехполюсными элементами используют графы четырехполюсников (рис. 2.15, б). Форму записи компонентных уравнений выбирают удобной для получения уравнений. В зависимости от выбора комбинации зависимых и независимых переменных (t/j, f/₂, /j, /₂) для пассивного четырехполюсника можно сформировать шесть вариантов записи компонентных уравнений: |А |, ||В |, ||G||, ||#||, ||У||, ||Z||. Наиболее часто используются формы ||Z||, | У||, | //1| и ||А||, которые выражаются следующими зависимостями:

Для одного и того же четырехполюсника существует взаимосвязь между параметрами в различных системах уравнений, которую несложно получить заменой переменных. В случае активных четырехполюсников при записи уравнений следует ввести источники, например при записи с Z-параметрами V_X и V_2X на разомкнутых зажимах (при 1 = 0, /₂ = 0) получим

В схемотехнике применяются различные соединения четырехполюсных преобразователей. В зависимости от способа соединения их входных и выходных зажимов различают следующие виды соединений: последовательно-последовательное, параллельно-последовательное, последовательно-параллельное, параллельно-параллельное. Для определения параметров результирующей схемы используют подходящую форму записи уравнений составляющих четырехполюсников. При обработке электрических сигналов распространено каскадное соединение преобразователей (рис. 2.16).

Условия соединения четырехполюсников t/₂ (1) = U 2 /₂ (1) = /| 2) делают удобными для их описания уравнения с Л-параметрами в матричной форме:

Если через А* 1 * и А* 2 * обозначить матрицы входящих четырехполюсников, то матрицу их каскадного соединения определяет соотношение А = а 1 >а 2 >.

Эффективным средством унификации формирования уравнений схем с четырехполюсниками служит их замена эквивалентными схемами с использованием двухполюсных элементов и зависимых

Рис. 2.16. Каскадное соединение четырехполюсников

Рис. 2.17. Эквивалентные схемы невзаимного (а) и обратимого (б) четырехполюсников

(управляемых) источников. Одним из распространенных приемов составления эквивалентной схемы четырехполюсника является преобразование его системы уравнений. Например, в уравнениях с //-параметрами слагаемые Н1 и H₂₂U₂ отражают взаимосвязь напряжений и токов одной ветви и их заменяют двухполюсниками R = #_и и g = #22> а слагаемые H₂U2 и Н₂1 моделируют с помощью зависимого источника напряжения, управляемого напряжением (ИНУН) с р = #₁₂, и зависимого источника тока, управляемого током (ИТУТ) с (3 = #21 (рис. 2.17, а).

Для обратимых (взаимных) четырехполюсников с симметричными матрицами коэффициентов возможно построение эквивалентных схем только на двухполюсных компонентах. Например, выполнение преобразований уравнений с Z-параметрами даст результат