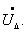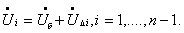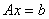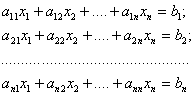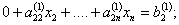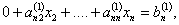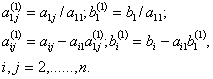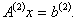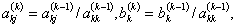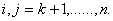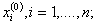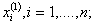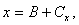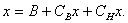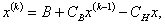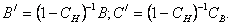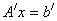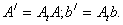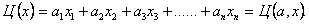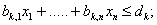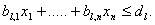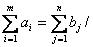Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Видео:Уравнение состояния идеального газа. 10 класс.Скачать

6. РАСЧЕТ РЕЖИМОВ СЛОЖНОЗАМКНУТЫХ СЕТЕЙ
Три основных матричных уравнения — обобщенное уравнение состояния, узловое и контурное уравнения определяют взаимосвязь параметров установившегося режима с параметрами электрической системы:
обобщенное уравнение состояния



Первая матрица соединений (инциденций) M характеризует соединение ветвей в узлах. Эта матрица является прямоугольной — число строк на единицу меньше числа узлов схемы, а число столбцов равно числу ветвей. Элементы матрицы равны Mij=1, если узел i является начальной вершиной ветви j, либо Mij=-1, если узел i является конечной вершиной ветви j и Mij=0, если узел не является вершиной ветви. Матрица токов в ветвях I — матрица столбец. Число ее элементов соответствует числу ветвей схемы замещения. Матрица задающих токов (токов нагрузок) J — матрица столбец с числом элементов на единицу меньше общего числа узлов. В выражение для второго закона Кирхгофа входит матрица соединения ветвей в независимые контуры N (вторая матрица инциденций) — это прямоугольная матрица, число строк ее равно количеству независимых контуров, а число столбцов равно числу ветвей схемы замещения. Элементы матрицы равны: Nij=1, если ветвь j входит в контур i и направление тока в ветви совпадает с направлением обхода контура, Nij=-1, если ветвь j входит в контур i и направление тока в ветви противоположно направлению обхода контура, Nij=0 если ветвь j не входит в контур i.
Матрица сопротивлений ветвей Z B в общем случае квадратная, а при отсутствии взаимоиндуктивной связи между элементами — диагональная, с числом строк равным числу ветвей схемы замещения. Матрица контурных ЭДС — матрица столбец с числом элементов равным числу независимых контуров схемы замещения. Матричное узловое уравнение связывает напряжения узлов относительно балансирующего с задающими токами и ЭДС в ветвях:

Информация о параметрах системы в узловых уравнениях содержится в матрицах проводимостей ветвей Y B и матрице узловых проводимостей Y Y. Матрица проводимостей ветвей это матрица обратная матрице сопротивления ветвей. Для диагональной матрицы элементы определяются через сопротивления ветвей


Матрица узловых проводимостей может быть сформирована по схеме замещения. Диагональный элемент Y yii равен сумме проводимостей ветвей связанных с i узлом. Недиагональный элемент ij равен проводимости ветви между узлами i и j с обратным знаком либо нулю, если непосредственная связь между узлами отсутствует.
Из матричного узлового уравнения определяются напряжения узлов относительно балансирующего

что позволяет определить токи в ветвях

Матричное выражение системы контурных уравнений связывает контурные токи (токи в хордах) с контурными ЭДС и задающими токами

Матрица контурных сопротивлений может быть вычислена через матрицу сопротивлений ветвей и вторую матрицу инциденций

либо сформирована по схеме замещения. Диагональные элементы являются суммой сопротивлений ветвей схемы, образующих соответствующий контур. Недиагональные
элементы Z K равны сумме сопротивлений, одновременно
входящих в контуры i и j, либо нулю при отсутствии общих ветвей. Слагаемое положительно при совпадении направлений обхода контуров на общей ветви и отрицательно в противоположном случае.
Сложные схемы последовательными упрощениями можно свести к простейшим замкнутым (сетям с двусторонним питанием). Совокупность упрощающих приемов сведена в методе преобразования. Для преобразования схем замещения используются следующие 
перенос нагрузок в другие узлы


эквивалентирование последовательных ветвей


эквивалентирование параллельных ветвей


преобразование треугольника в звезду






преобразование звезды в треугольник





Рис.6.1. Приемы метода преобразования сети.
Пример 6.1. Применение узловых уравнений для расчета сложнозамкнутой сети.
Рис.6.2. Схема замещения сложнозамкнутой сети.
Для аналитического представления схемы замещения определим матрицу узловых проводимостей схемы через первую матрицу инциденций и матрицу проводимостей ветвей схемы замещения:



Выполним операцию обращения матрицы узловых проводимостей классическим методом. Количество элементов в искомой матрице соответствует количеству элементов исходной. Необходимо вычислить значение одного определителя третьего порядка и шести второго. При введении элементов в комплексной форме этот подход может оказаться наиболее рациональным. Для этого предварительно находим значение определителя;
Определяем значения элементов обратной матрицы. Учитываем симметрию получаемой матрицы, что объясняется симметрией исходной матрицы узловых проводимостей:





Формируем обратную матрицу из вычисленных значений элементов;

Определяем матрицу токов нагрузок по значению номинального напряжения сети и мощностям нагрузок узлов

Определяем разность напряжений узлов и узла баланса в первом приближении

Это позволяет найти напряжения узлов;

Уточняем значения токов узлов по уточненным напряжениям узлов:
Уточняем значения падений напряжений. Дальнейших уточнений при анализе режимов работы сетей 110 кВ не требуется:

Определяем уточненные значения напряжений узлов

Определяем токи в ветвях схемы сети

Пример 6.2. Применение метода преобразования для расчета сложнозамкнутой схемы.
Применим метод преобразования к схеме замещения с одним источником электроэнергии A, семью нагрузками узлов и десятью ветвями. На первом этапе преобразуем схему к простейшей замкнутой схеме.
Перенесем нагрузки из узлов 2 и 7 в узлы 1 и 6:


После исключения нагрузок, возможно заменить сопротивления ветвей 12,27 и 67 эквивалентным

Заменим сопротивления треугольника между узлами 1, 4 и 6 на сопротивления эквивалентной звезды

Рис.6.3. Порядок изменения схемы при использовании приемов метода преобразования электрической сети.

Исключаем нагрузки из узлов 4, 5 и 6 путем их переноса в узлы 3 и 8, эквивалентируем образующиеся после этого последовательно включенные сопротивления:



После этих действий возможна замена эквивалентным сопротивлением ветвей 34, 48, 35, 56, 68:

В результате преобразований схема сведена к простейшей замкнутой схеме (кольцевой). Определяем мощности на головных участках схемы по известным выражениям:


Последовательно возвращаемся к исходной схеме и определяем искомые параметры режима.
Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Обобщенное уравнение состояния электрической сети
Некоммерческое акционерное общество
АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра “ Электрические станции, сети и системы ”
МАТЕМАТИЧЕСКИЕ ЗАДАЧИ И КОМПЬЮТЕРНОЕ
МОДЕЛИРОВАНИЕ В ЭЛЕКТРОЭНЕРГЕТИКЕ
для студентов всех форм обучения специальности
СОСТАВИТЕЛИ: Ж. К. Оржанова., К.К.Тохтибакиев. Математические задачи и компьютерное моделирование в электроэнергетике. Конспект лекций для студентов всех форм обучения специальности 050718 – Электроэнергетика.- Алматы: НАО АИЭС, 2008.- 26с.
В конспекте лекций рассмотрены: применение алгебры матриц и теории графов к анализу сетей электрических систем, основные подходы к математическому исследованию переходных процессов в автоматически регулируемых энергосистемах.
В данном курсе лекции рассматриваются вопросы режимов электрических систем, т.е. излагаются некоторые математические методы и приемы, непосредственно применяемые в электрических системах. Так, например, не рассматриваются режимы электрических станций, поведение собственных нужд станций при авариях, релейной защиты электрических систем и средств их автоматики, конструирование регулирующих и управляющих устройств. Цель дисциплины – это связать математику как общетеоретическую дисциплину с практическими ее применениями в работе инженера и дать конкретный практический аппарат для инженерных исследований. Задачи дисциплины — заблаговременная подготовка студентов к восприятию математических вопросов в специальных курсах и сознательному применению математики при решении различных электроэнергетических задач, позволяющие выбрать необходимые методы и приемы, которые дают достоверные результаты и наиболее быстро ведут к цели.
В качестве аппарата решения некоторых специальных задач электрических систем наиболее важными являются:
1) анализ электрических цепей с понятием о методах теории графов и элементах топологии применительно к электрическим сетям и системам;
2) некоторые приемы определения вероятностей;
3) способы анализа некоторых дифференциальных уравнений, используемых при выяснении устойчивых состояний системы.
Дисциплина «Математические задачи и компьютерное моделирование в электроэнергетике» является обязательным базовым предметом для бакалавров высших учебных заведений, обучающихся по специальности 050718 –«Электроэнергетика».
Дисциплина базируется на математической и электротехнической подготовке студентов в предшествующих семестрах и на знаниях, полученных при изучении математики, физики, инженерной и компьютерной графики, теоретических основах электротехники, механики.
1 Лекция 1. Математические задачи и компьютерное моделирование в электроэнергетике. Постановка и основные задачи курса и математические методы их решения
– определение параметров электроэнергетических систем, понятие устойчивости в электроэнергетике, составление математических моделей отдельных элементов систем.
– изучение электрических схем, принципиальных схем, схем замещения.
Под электрической системой (ЭС) понимается электрическая часть энергетической системы, т.е. совокупность элементов, вырабатывающих, преобразующих, передающих, распределяющих и потребляющих электрическую энергию (ээ).
Электрическая сеть – это совокупность электроустановок для распределения электрической энергии, состоящая из подстанций, распределительных устройств, воздушных и кабельных линий электропередачи. По электрической сети осуществляется распределение электроэнергии от электростанций к потребителям.
Линия электропередачи (ЛЭП) (воздушная или кабельная) – электроустановка, предназначенная для передачи электроэнергии.
Математическое описание электроэнергетической системы имеет свою специфику и отличается от теплоэнергетической и гидроэнергетической части системы. При составлении математического описания учитывают, что электрическая система включает в себя силовые элементы – генераторы, трансформаторы, преобразователи, нагрузки и электрические сети (высокого напряжения, содержащие линии передач, среднего напряжения, распределительные с относительно низким напряжением).
Электрическая система содержит также элементы управления, изменяющие и регулирующие состояние системы или режим системы. Для расчета режима системы необходим математический аппарат. Взаимодействуя между собой, элементы системы в любой момент связаны единством процессов производства, передачи, распределения и потребления электрической энергии. При этом под процессами понимают отдельные составляющие явления, отражающие некоторые связи между переменными величинами, которые отвечают явлениям, свойственным данному состоянию (или режиму) системы.
Чтобы дать математическое описание системы, надо в виде математической модели представить все связи между переменными величинами процессов. Изучение этих процессов, направлена на обеспечение лучшей работы системы, основная задача которой – выработка электрической энергии.
Энергия – это количественный показатель работы электрической системы. Качество энергии характеризуется главным образом величиной и частотой напряжения у потребителя. Режим системы – это ее состояние в любой момент времени или на некотором интервале времени. Режим системы определяется указанными показателями и другими показателями. Параметры режима – показатели, зависящие от изменения режима. К параметрам режима относятся напряжения в различных точках системы, токи в ее элементах, углы расхождения векторов ЭДС и напряжений, активные и реактивные мощности и т.д.
При анализе и составлении математического описания различают три основных вида режимов электрических систем:
нормальный установившийся режим, применительно к которому проектируется электрическая система и определяются технико-экономические характеристики;
послеаварийный установившийся режим, наступающий после аварийного отключения какого-либо элемента или ряда элементов системы. Перечисленные установившиеся режимы характеризуются параметрами, не изменяющимися во времени. При этом связи между параметрами режима представляются алгебраическими уравнениями;
переходный режим , во время которого система переходит из одного состояния к другому. Для него характерно изменение всех его параметров во времени и описание его дифференциальными уравнениями.
Любой режим состоит из множества различных процессов .
Параметры режима электрической системы связаны между собой соотношениями, называемыми параметрами системы.
Параметp ы системы – это показатели количествен н о опреде ля ющиеся физическими свойствами элементов системы, с хемой их соединений. К параметрам системы относятся значения co противлений, проводимосте й элемен т ов, ко эффиц иентов трансфор мации, пост оя нныx вр е мени и т.п.
Если параметp ы системы зависят от изменений ее режима, то система называется нелинейной. Параметры всех реальных электрических систем нелинейны. Но математический аппарат для их исследования еще недостаточно разработан. Поэтому, параметры системы часто полагают постоянными, считая систему на каком-то исследуемом участке линейной.
Схема замещения является математическим инструментом инженера. В зависимости от того, какая электрическая сеть и какие процессы интересуют, инженер подбирает схему замещения изучаемой сети. После подбора схемы замещения, расчет состояния электрической системы (режима) сводится к расчету электрической цепи.
Переходные режимы делятся на нормальные (эксплуатационные) и аварийные. Нормальные переходные процессы обусловлены изменениями нагрузки системы и реакцией на них регулирующих устройств. Нормальные переходные процессы, которые возникают при обычных эксплуатационных операциях: включении и отключении трансформаторов, а также отдельных линий электропередач; эксплуатационных изменениях схемы коммутации системы; включении и отключении отдельных генераторов и нагрузок или изменениях их мощности. При нормальных переходных процессах для описания системы применяют линейные дифференциальные уравнения.
Аварийные переходные процессы возникают вследствие каких-либо резких аварийных изменений режима: при коротких замыканиях элементов системы, изменении схемы соединения системы, случайном отключении агрегатов или линий электропередачи, несущих значительные нагрузки. Такие изменения в математической теории электрических систем, называемые большими возмущениями или воздействиями, приводят к значительным отклонениям параметров режима от их исходного состояния.
При исследовании переходных режимов особое значение имеет проблема устойчивости электрических систем. Рабочее состояние электрической системы, называемое установившимся режимом, должно обладать свойством устойчивости, т.е. способностью восстанавливать исходный установившийся режим или режим, близкий к нему, после какого-либо его изменения – отклонения (возмущение: малые изменения мощности нагрузки, большие изменения мощности, выдаваемой генератором при коротких замыканиях, отключениях электропередач и т.д.). Степень устойчивости системы уменьшается с увеличением нагрузки (мощности, выдаваемой ее генераторами) и понижением напряжения (увеличением мощности потребителей, снижением возбуждения генераторов). Для каждой системы определяются некоторые значения величин – параметров режима, характеризующих предел устойчивости.
Система должна работать не достигая этого предела, т.е. с некоторым запасом устойчивости, определяемым специальными нормативами или послеаварийных условий.
При анализе устойчивости электрических систем различают три ее вида: статическую, динамическую и результирующую.
Статическая устойчивость – способность системы восстанавливать исходное состояние после малого его отклонения (возмущения). Под малым понимается такое отклонение, при котором исследуемая электрическая система может изучаться на основе систем линейных дифференциальных уравнений с применением общих методов Ляпунова, способов малых колебаний, предусматривающих исследование характеристических уравнений и применение частотных характеристик, включая различные приемы построения границ области устойчивости.
Динамическая устойчивость – способность системы восстанавливать исходный режим или практический близкий к нему после большого возмущения (короткого замыкания, отключения линии и т.д.). При анализе динамической устойчивости для выявления изменений параметров режима составляют нелинейные, трансцендентные уравнения высоких порядков. Для этого применяют аналоговые вычислительные машины и расчетные модели переменного тока, снабженного автоматикой.
Результирующая устойчивость – способность системы восстанавливать исходный режим или практический близкий к нему после нарушения в течение некоторого времени синхронной работы с последующим ее восстановлением без отключения основных рабочих элементов системы.
2 Лекция 2. Математические модели установившихся режимов электрической системы. Уравнения установившегося режима электрической системы
– определение схемы замещения, у равнения состояния линейной электрической сети, формирование матричных уравнений состояния электрической цепи.
– исследование режима электрической системы, законы Ома и Кирхгофа в матричной форме, математические модели переходных процессов в электроэнергетике.
Анализ условий работы электрической системы требует расчета ее установившихся режимов, целью которого является определение параметров режима: напряжения в узловых точках, токов и мощностей протекающих по отдельным ее элементам.
Основные элементы электрической системы в расчетах установившихся режимов представляются схемами замещения, состоящими из элементов электрической цепи: источников напряжения или тока и сопротивлений. К схеме замещения применимы такие понятия как ветвь, узел и контур. Схемы замещения содержащие контуры, называются замкнутыми, в обратном случае – разомкнутыми.
Состояние линейной электрической цепи описывается уравнениями Ома и Кирхгофа.
Закон Ома определяет взаимосвязь параметров каждой из ветвей цепи. Для i -й ветви, характеризующейся сопротивлением Zi , действующей в ней ЭДС Е i и протекающим по ней током Ii , разность потенциалов между ее концами (падение напряжения на ветви) UBi определяется в соответствии с уравнением
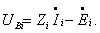
Первый закон Кирхгофа определяет баланс токов в каждом узле цепи, алгебраическая сумма токов в узле равна нулю. Для произвольного узла, содержащего источник тока J и связывающего k ветвей, уравнение имеет вид
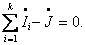
Второй закон Кирхгофа определяет баланс напряжений в контурах цепи, алгебраическая сумма падений напряжения на ветвях контура равна нулю. Для произвольного контура, содержащего l ветвей, уравнение имеет вид
Схема замещения электрической системы обычно является связанным направленным графом. Она состоит из ветвей (ребер), соединенных в узлы (вершины). Ветви образуют цепочки (пути графа), которые могут быть замкнутыми. Все величины, характеризующие состояние ветвей (ЭДС, токи, падения напряжения), имеют определенное направление.
Для направленного графа могут быть определены: 1) матрица соединений ветвей в узлах (первая матрица инциденций); 2) матрица соединений ветвей в независимые контуры (вторая матрица инциденций).
Матрица соединений ветвей в узлах – это прямоугольная матрица, число строк которой равно числу вершин графа n , а число столбцов – числу ребер m.
Матрица соединений ветвей в независимые контуры – это прямоугольная матрица, число строк которой равно числу независимых контуров графа k, а число столбцов – числу ветвей m.
Матрицы М и N дают возможность записать уравнения состояния электрической цепи в матричной форме.
Первый закон Кирхгофа в матричной форме
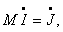
где 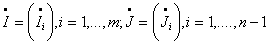
Второй закон Кирхгофа в матричной форме
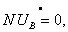
где 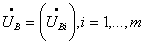
Чтобы ввести в уравнения второго закона Кирхгофа токи в ветвях схемы замещения, воспользуемся законом Ома, который выражается матричным уравнением:
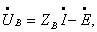
где ZB – диагональная матрица сопротивлений ветвей; Е – ЭДС в ветвях.
Для формирования обобщенного уравнения состояния необходимо предварительно определить матрицы соединений М и N , которые в аналитической форме отображают конфигурацию схемы замещения электрической сети.
Для составления матрицы М S достаточно пронумеровать все узлы и ветви схемы и в каждом столбце матрицы записать (+1) и (-1) в тех строках, которые соответствуют соединяемым данной ветвью узлам, а в остальных элементах столбцах записать «0». Вычеркиванием строки соответствующей балансирующему узлу, получаем искомую матрицу М.
Для составления матрицы N , предварительно требуется выделить независимые контуры, количество которых 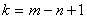
Задачей расчета установившегося режима электрической системы является определение токов в ветвях схемы замещения, напряжений в ее узловых точках и соответствующих им мощностей. Для этого составляется обобщенное уравнение состояния, которое решается относительно токов в ветвях. По найденной матрице 
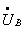
Достаточно знать падения напряжения на ветвях схемы, чтобы определить падения напряжения на остальных ветвях и напряжениях всех узлов относительно балансирующего, т.е. и напряжения узлов, если напряжение балансирующего узла 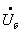
Если начинать расчет с определения напряжений в узлах схемы относительно балансирующего (матрицы 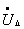
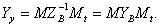
Квадратная матрица (7) порядка ( n -1) называется матрицей узловых проводимостей. Она дает возможность получить окончательную форму записи системы узловых уравнений
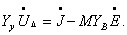
Решив уравнение (2.8) относительно 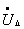
Порядок расчета системы узловых уравнений матричным методом. Для выбранной схемы составляется:
— диагональная матрица узловых токов схемы;
— диагональная матрица проводимости ветвей;
— заполняется матрица инциденций нулями и единицами.
3 Лекция 3. Методы решения уравнений состояния электрической системы
– определение точных и приближенных методов решения линейных алгебраических уравнений;
– решение уравнений состояния методом Гаусса.
– обращение матрицы коэффициентов уравнений состояния;
– решение уравнений состояния итерационным методом.
Расчеты установившихся режимов необходимы при выборе конфигурации схемы электрической системы и параметров ее элементов, анализе устойчивости и оценке токов коротких замыканий, определении экономичных режимов ее работы.
Для выполнения расчета любого установившегося режима необходима информация о схеме и параметрах сети электрической системы, о потребителях (нагрузках) и источниках электроэнергии (электростанциях).
Уравнения установившегося режима электрической системы, связывающие мощности, задающие токи и напряжения узлов, при отсутствии ЭДС в ветвях имеют вид
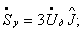
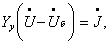
где 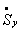
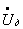
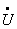
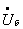
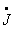
Система нелинейных (3.1) и линейных (3.2) уравнений при заданных мощностях узлов в общем случае может быть решена только итерационным методом. При этом возможны два подхода к решению:
— поочередное решение уравнений (3.1) и (3.2) в общем итерационном цикле;
— объединение этих уравнений в единую систему нелинейных уравнений и последующее ее решение.
В первом случае решение производится по следующей схеме:
1) задаются начальными приближениями напряжений узлов;
2) по значениям напряжений и заданным значениям мощностей (3.1) определяются задающие токи;
3) решается система линейных уравнений (3.2) при известных значениях задающих токов относительно напряжений в узлах;
4) на основе полученных значений напряжений в узлах выполняется следующий шаг итерационного процесса начиная с п.2.
Условием окончания итерационного процесса является близкое совпадение напряжений на двух последующих итерациях, а также совпадение вычисленных по (3.1) значений мощностей узлов с заданными.
Во втором случае уравнения (3.1) и (3.2) объединяются путем подстановки задающих токов либо из (3.2) в (3.1), что приводит к системе вида
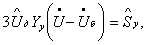
либо из (3.1) в (3.2)
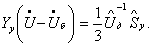
Как при первом, так и при втором подходе на каждом шаге итерационного процесса решается система линейных алгебраических уравнений либо непосредственно в виде узловых уравнений (3.2), либо в виде линеаризованных уравнений (3.3) и (3.4).
Методы решения систем линейных алгебраических уравнений делятся на две группы: прямые и итерационные. К прямым относятся методы, позволяющие получить решение в результате конечного числа арифметических операций, зависящего от вычислительной схемы, а также от порядка и структуры матрицы коэффициентов системы уравнений. Методы этой группы называются также точными, т.к. если исходные данные заданы точно и вычисления точны, то решение также получается точным.
К итерационным относятся методы, с помощью которых решение системы линейных алгебраических уравнений получается как предел последовательных приближений, вычисляемых посредством единообразных операций. Эти методы называются приближенными, т.к. вычисления ведутся без округлений, позволяют получить решение системы уравнений лишь с заданной точностью.
В основе всех прямых методов решения линейных алгебраических уравнений установившегося режима электрической системы (УУР) лежит метод последовательного исключения неизвестных, называемый методом Гаусса. К числу наиболее характерных вычислительных схем этого метода относятся алгоритмы с обратным ходом и без обратного хода.
Алгоритм метода Гаусса с обратным ходом. Решение системы n линейных уравнений вида
по этому алгоритм состоит из двух этапов. На первом этапе (прямой ход) исходная система за n однотипных шагов преобразуется таким образом, что матрица коэффициентов преобразованной системы становится верхней треугольной, т.е. все элементы, расположенные ниже ее главной диагонали, равны нулю. На втором этапе (обратный ход) последовательно определяются значения неизвестных от х n до х1.
Последовательность операций, выполняемых при прямом ходе:
На первом шаге исходной системе уравнений
новое уравнение делится на а11. Далее х1 исключается из всех последующих уравнений (i=2. n) путем умножения первого уравнения каждый раз на аi1 и вычитается из i-го уравнения. В результате этих операций получается система уравнений с матрицей коэффициентов А (1) :
Выполнение операций первого шага требует, чтобы элемент а11, называемый ведущим был отличен от нуля.
Второй шаг состоит в исключении х2 из уравнений 3,……,n, полученной на первом шаге системы путем выполнения аналогичных операций при использовании в качестве ведущего элемента 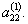
Третий и последующий шаги выполняются аналогично. Формулы для расчета коэффициентов системы уравнений на произвольном (k-м) шаге запишутся как
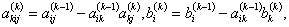
На последнем шаге (k=n) второе из выражений (3.5) определяет 
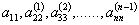
В общем виде формулы для обратного хода записываются

Итерационные методы решения систем линейных алгебраических уравнений позволяют получить значения искомых неизвестных в результате многократного выполнения единообразных шагов вычислений, называемых последовательными приближениями или итерациями. Рассмотрим два итерационных метода решения систем линейных алгебраических уравнений (метод простой итерации и метод Зейделя). Эти методы допускают простое обобщение на решение нелинейных уравнений установившегося режима, связывающих мощности и напряжения в узлах электрической системы.
Метод простой итерации. Исходная система линейных алгебраических уравнений
в предположении, что 

Система уравнений (3.7) согласно методу простой итерации решается следующим образом:
1) задаются начальными (нулевыми) приближениями неизвестных
2) значения 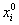
3) подстановкой полученных значений 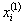
Таким образом, на k-м шаге итерационного процесса система (3.7) запишется как

Итерационный процесс продолжается до тех пор, пока значения 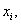
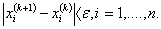
Для выполнения условия (3.9) при любой заданной точности решения, т.е. при любом сколь малом значении e , необходимо, чтобы
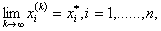
где 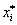
При выполнении (3.10) для произвольного начального приближения 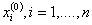
Необходимые и достаточные условия сходимости итерационного процесса по методу простой итерации (3.13), так и только достаточные условия (3.14а) и (3.14б) определяются соотношением элементов матрицы коэффициентов А и не зависят ни от значений элементов столбца правых частей b, ни от начального приближения х (0) .
Метод Зейделя. Этот метод, так же как и метод простой итерации, базируется на использовании уравнений, приведенных к виду (3.7). В отличие от метода простой итерации для вычисления i-й переменной на каждом k-м шаге итерационного процесса используются значения переменных, вычисленные как на предыдущем (k-1)-м шаге, так и на данном. При этом на k-м шаге итерационного процесса система (3.7) имеет вид:

Для выяснения условий, определяющих сходимость итерационного процесса по методу Зейделя, как и ранее, представим (3.7) в матричной форме записи:
где В – столбец; С – квадратная матрица с нулевыми диагональными элементами.
Представим С в виде суммы верхней (Св) и нижней (Сн) треугольных матриц, получим:
В соответствии с этим представим итерационный процесс (3.16) в матричной форме:
или 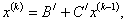
где
Выражение (3.17) аналогично выражению (3.11), полученному для метода простой итерации. Следовательно, для сходимости итерационного процесса по методу Зейделя, необходимо и достаточно, чтобы собственные значения матрицы С / по абсолютной величине были меньше единицы. Поскольку матрицы С и С / по-разному выражаются через компоненты матрицы А, то условия сходимости метода Зейделя и метода простой итерации в общем случае различны, т.е. существуют такие матрицы А, для которых итерационный процесс по методу Зейделя сходится, а по методу простой итерации не сходится, и наоборот.
Достаточные условия сходимости метода простой итерации являются достаточными и для метода Зейделя. Если эти условия выполняются, то процесс по методу Зейделя сходится.
Известно, что при положительно-определенной матрице А итерационный процесс по методу Зейделя всегда сходится. Следовательно, если матрица А – положительно-определенная, то сходимость гарантируется; если нет, то исходную систему можно привести к эквивалентной с положительно-определенной матрицей коэффициентов путем умножения слева на транспонированную матрицу А, т.е. путем перехода от системы Ах= b к системе 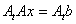
где
Если исходная система имеет решение, т.е. если А – неособенная, то матрица А / — положительно-определенная и итерационный процесс по методу Зейделя сходится к решению.
4 Лекция 4. Применение линейного программирования в энергетике
— области применения и основные приемы решения. Составление математической модели и методы нахождения опорного плана транспортной задачи. Метод потенциалов.
— решение открытых транспортных задач и транспортных задач с промежуточными перевозками. Транспортные задачи в сетевой постановке с использованием метода границ и ветвей.
— изучение задач линейного программирования в энергетике, формирование экстримальных задач в форме транспортных, методы их решений.
Задача линейного программирования математически может быть представлена следующим образом. Пусть математическая модель записана в виде линейного соотношения
Надо найти значения х1, ……,хn, при которых может быть обеспечено экстремальное значение функции Ц(х), при ограничениях
В ограничения, присутствующие в задачах линейного программирования, иногда вводят также ограничения в виде условий неотрицательности всех или части переменных xj≥0, j=1. p.
Целевую функция Ц(а,х) иногда называют критерием или функционалом задачи линейного программирования.
Одной из наиболее распространенных задач линейного программирования является так называемая транспортная задача. При решении этой задачи отыскивается наиболее экономичный способ перевозки каких-либо продуктов со складов к потребителям, причем принимается, что известны затраты на перевозку единицы продукта к потребителям продукта в заданных пунктах реализации.
Постановка транспортной задачи в матричной форме. Формулировка транспортной задачи по критерию стоимости приведена ниже. В m пунктах производства А1, …. Аm находится однородный продукт (сахар, уголь, картофель и т.д.)в количествах соответственно а1,…. аm, который должен быть доставлен n потребителям В1,….,Вn в количествах b1,…. bn. Известны транспортные издержки сij (расходы), связанные с перевозкой единицы продукции из пункта Аi в пункт Вj.
Для разрешимости поставленной задачи необходимо и достаточно, чтобы сумма запасов равнялась сумме спроса всех пунктов, т.е.
Для наглядности транспортную задачу представим в виде таблицы, которая называется распределительной (см. таблицу 4.1).
Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Введение
Целью данного курса является ознакомление студента с основными разделами прикладной математики, которые находят наибольшее применение при решении базовых задач, связанных с управлением и проектированием электроэнергетических систем. Это позволяет связать математику как общетеоретическую науку с ее применением в инженерной практике и научных исследованиях, сформировать грамотный технический подход к решению инженерных и научных проблем, а также подготовить студента к более глубокому и критическому восприятию специальных дисциплин.
В курсе “Математические задачи электроэнергетики” будут представлены основные научные достижения в области управления таким сложным объектом как электроэнергетическая система (ЭЭС), рассмотрены возможности современной математики и вычислительной техники, позволяющие смоделировать реальные процессы, происходящие в ЭЭС.
В пособии представлены программа курса с ссылками на литературу, задание на выполнение контрольной работы для студентов заочного отделения, методические указания для проведения расчетов вручную и с использованием ЭВМ. Материал, изложенный в пособии может быть использован также студентами дневного отделения ФЭН при подготовке в практическим занятиям по курсу.
1.Программа курса с указанием используемой литературы.
Техническая постановка задачи расчета и анализа
установившихся режимов электрических систем.
Электрическая система (ЭС) как объект математического моделирования. Понятие режима работы ЭС. Виды режимов. Параметры режима функционирования ЭС. Общая характеристика разделов прикладной математики, используемых при решении задачи расчета установившихся режимов ЭС ([1]с.7-30,[2]c.5 — 6).
Уравнения состояния электрических систем
1.2.1 Понятие схемы замещения электрической системы. Схемы замещения источников энергии, потребителей и элементов электрической сети. Пример перехода от реальной схемы электрической системы к схеме замещения. Моделирование электрической сети с помощью направленного графа ([1]c.31-33,37-38,[2]c.6-10,[3]c.109-111).
1.2.2. Использование матричных методов прикладной математики для моделирования процессов, происходящих в электрической системе. Основы матричной алгебры. Действия с матрицами. Виды матриц, используемых при расчете установившихся режимов. Матрицы инциденций первого и второго рода. Правила формирования матриц инциденций, исходя из структуры электрической сети, представленной в виде графа. Матрицы режимных параметров ([5]c.35-52,[1]c.38-40,[2]c.10-13,[3]c.114-118).
1.2.3 Виды уравнений состояния электрической системы. Представление в матричной форме основных законов электротехники: закона Ома, первого и второго законов Кирхгофа. Получение обобщенного уравнения состояния на основе двух законов Кирхгофа. Уравнения узловых напряжений. Структура и физический смысл элементов матрицы узловых проводимостей. Контурные уравнения состояния ЭС. Преимущества и недостатки различных форм представления уравнений состояния с учетом удобства реализации алгоритмов на ЭВМ ([1] c.40-42, c.48-56, [2] c.13-30, [3] c.118-129,[4]c.25-35).
1.3. Методы решения уравнений состояния электрических систем.
1.3.1. Математическая модель задачи расчета и анализа установившихся режимов ЭС. Способы представления параметров генераторных и нагрузочных узлов схемы замещения электрической системы. Классификация методов решения систем уравнений состояния ([1]c.70-74,[2]c.30-33, [4]c.8-14,c.35)
1.3.2. Характеристика прямых методов решения уравнений состояния, представленных в виде систем линейных алгебраических уравнений. Алгоритм метода Гаусса с обратным ходом и без обратного хода. Анализ точности полученного решения по сумме невязок. Факторы, влияющие на точность решения систем уравнений методом Гаусса. Применение метода Гаусса для решения системы линейных уравнений узловых напряжений.([1] c.79-88, [2] c.34-36, [4] c.35-39).
1.3.3. Общая характеристика итерационных методов решения систем уравнений. Понятие итерационного процесса. Виды итерационных процессов. Критерии сходимости итерационных процессов. Метод простой итерации. Метод Зейделя и его применение для решения систем линейных уравнений узловых напряжений. Сравнительная характеристика итерационных методов с учетом их реализации на ЭВМ ([1] c.91-101, [2]c.37-38,[4] c.43-50).
1.3.4. Нелинейные уравнения установившегося режима. Представление нелинейных уравнений состояния в форме баланса токов и в форме баланса мощностей. Использование метода Зейделя для решения систем нелинейных уравнений состояния. Метод Ньютона. Графическая интерпретация метода Ньютона для функции одной переменной. Алгоритм метода Ньютона для функции многих переменных([4]c.57-60,c.64-76).
1.4.Анализ статической устойчивости электрических систем.
1.4.1.Понятие устойчивости применительно к электрической системе. Состояние устойчивого равновесия. Дифференциальные уравнения, описывающие изменение параметров системы во времени. Понятие свободной и вынужденной составляющих. Определение статической устойчивости как устойчивости в малом. Метод малых колебаний ([1]с.173-175,[2] c.39-41,[6]c.189-190).
1.4.2 Анализ статической устойчивости по корням характеристического уравнения. Характеристическое уравнение системы. Теорема Ляпунова. Графики изменения свободной составляющей в зависимости от корней характеристического уравнения. Пример анализа статической устойчивости системы «станция — шины бесконечной мощности» при подключении к узлу синхронного неявнополюсного генератора ([1]c.175-181, [2]c.41-44,[6]c.190-194).
1.4.3 Анализ статической устойчивости на основе алгебраических критериев. Понятие критерия устойчивости. Алгебраические критерии устойчивости. Необходимые и достаточные условия устойчивости системы. Критерий устойчивости Гурвица. Алгоритм составления определителя Гурвица по характеристическому уравнению системы. Примеры использования критерия Гурвица для характеристических уравнений 1-го-4-го порядков ([1]с.181-188,[2]c.44-47,[6]c.195-198).
1.4.4 Анализ статической устойчивости на основе частотных критериев. Частотные критерии анализа устойчивости. Принцип аргумента. Понятие годографа характеристического уравнения. Критерий устойчивости Михайлова. Примеры типовых годографов для устойчивых, неустойчивых систем. Граница колебательной и апериодической устойчивости. Пример использования критерия Михайлова для характеристического уравнения 3-го порядка ([1] c.188-196, [2] c.47-49).
2.ОСНОВЫ РАСЧЕТА И АНАЛИЗА УСТАНОВИВШИХСЯ РЕЖИМОВ
Техническая постановка задачи.
Расчет и анализ установившихся режимов электроэнергетических систем (ЭЭС) является одним из наиболее существенных этапов в процессе принятия оптимальных решений как при проектировании, так и управлении ЭЭС.
Постановка задачи расчета режима функционирования определяется особенностями ЭЭС как сложной технической системы, которая включает в себя большое количество элементов, вырабатывающих, преобразующих, передающих, распределяющих, потребляющих электроэнергию и образующих сложно-замкнутую разветвленную структуру. В процессе расчета и анализа режимов приходится учитывать также специфику функционирования ЭЭС, обусловленную такими факторами как непрерывность процесса производства, распределения и потребления электроэнергии; динамизм, т. е. постоянное изменение технологических характеристик; сложность структурных связей и наличие системных особенностей.
Режимом работы ЭЭС называется состояние системы в любой момент времени или на некотором интервале времени.
Под установившимся режимом понимается такое состояние ЭЭС, когда параметры системы на рассматриваемом интервале времени сохраняются неизменными или изменяются достаточно медленно.
В современных условиях расчет установившихся режимов ЭЭС является наиболее часто решаемой задачей. При проектировании ЭЭС расчет установившихся режимов производится с целью выбора и уточнения параметров проектируемой системы. В процессе эксплуатации подобные расчеты позволяют оперативно управлять и прогнозировать работу ЭЭС. При этом осуществляется оценка допустимости режима по техническим условиям оборудования и определение режимов, оптимальных по технико-экономическим критериям.
Задача расчета установившихся режимов ЭЭС сводится к определению совокупности параметров, характеризующих работу системы: напряжений в различных точках системы, токов в ее элементах, потоков и потерь мощности и т. д.
Проведение расчета связано с рядом основных этапов:
- предварительное преобразование и переход к расчетной схеме электрической системы; формирование уравнения состояния по известным исходным данным с учетом структуры расчетной схемы; выбор метода расчета, составление алгоритма и программы на ЭВМ; проведение расчета установившегося режима на ЭВМ; анализ точности полученных результатов.
В основе решения задачи расчета режима лежит математическое моделирование реальных процессов, происходящих в ЭЭС. При этом могут быть использованы линейные модели (например, обобщенное уравнение состояния, уравнения узловых напряжений, уравнения контурных токов [1]) и нелинейные модели (например, уравнения узловых напряжений в форме баланса мощности и в форме баланса токов [2]).
Расчет установившегося режима с использованием
линейных математических моделей.
В качестве примера рассмотрим реальную схему электрической системы (рис.2.1), которая включает в себя тепловую электростанцию (ТЭС), линии электропередач различных номинальных напряжений (Л1-Л6), понизительные подстанции и обобщенные нагрузки (Н1-Н4).
Предварительным этапом перед проведением расчета установившегося режима является переход от принципиальной к схеме замещения, а затем к расчетной схеме, формируемой на основе теории графов.
Под схемой замещения ЭС понимается совокупность схем замещения отдельных элементов, соединенных в той же последовательности, что и в реальной схеме.
Теория формирования схем замещения рассматривается в специальных курсах. Ограничимся примером формирования схемы замещения простейшей электрической системы, в объеме необходимом для понимания структуры расчетной схемы.
Будем рассматривать симметричные установившиеся режимы, при которых используется схема замещения одной фазы.
Принципиальная схема любой ЭС включает в себя три группы элементов:
- источники энергии, потребители или нагрузку электрические сети, соединяющие источники с потребителями.
Возможны следующие варианты схем замещения для источников энергии: источник напряжения с ЭДС и внутренним сопротивлением 
Потребители электроэнергии (нагрузка) моделируются с помощью следующих схем замещения : сопротивление нагрузки Z (рис.2.3,а); источник тока J, равный взятому с обратным знаком току нагрузки (рис.2.3,б); задающий ток J, равный току источника тока (рис.2.3,в);
Схемы замещения элементов электрической сети представляют собой сопротивления Z, причем схемы замещения трансформаторов подстанций объединяются со схемами замещения источников энергии и нагрузок.
С учетом рассмотренных схем замещения отдельных элементов, приведем вариант схемы замещения (рис.2.4) электрической системы, представленной на рис.2.1.
При этом произведем, известные из курса ТОЭ, преобразования: приведем схемы к одному номинальному напряжению, схемы замещения трансформаторов подстанций объединим со схемами замещения источников питания и нагрузок; смоделируем нагрузку и генерацию мощности с помощью задающих токов.
Введены обозначения полученных в ходе преобразования сопротивлений и узлов схемы замещения, из которых один узел генераторный и 4 узла — нагрузочных.
По такой схеме замещения может быть составлен топографический направленный граф, который используется как расчетная схема (рис.2.5).
Данная расчетная схема содержит четыре независимых узла (1, 2, 3, 4) и один балансирующий узел (Б). Задающие токи в узлах 1,2,3,4 моделируют нагрузку и имеют отрицательные значения. В качестве балансирующего выбран генераторный узел, в котором задано значение напряжения
Расчетная схема содержит два независимых контура (I, II), направление обхода каждого заданно произвольно.
Схемы замещения современных электрических систем имеют сотни узлов и ветвей, образующих сложно-замкнутую структуру. Расчет режимов функционирования подобных технических систем невозможен без использования вычислительной техники. Поэтому важное значение приобретает использование единого формализованного подхода, основанного на аппарате алгебры матриц и позволяющего дать описание схем любой сложности и конфигурации. Матричная форма представления обеспечивает компактность и наглядность представления большого количества исходной и результирующей информации при проведении расчета режимов сложных схем.
2.3 Уравнения состояния ЭС.
Основные формы уравнений состояния ЭЭС: обобщенное уравнение состояния, уравнения узловых напряжений, контурные уравнения подробно описаны в [1].
В качестве примера линейных математических моделей рассмотрим наиболее широко используемые на практике формы уравнений состояния — обобщенное уравнение состояния и уравнение узловых напряжений в матричной форме или в виде системы уравнений, которые описывают нормальный режим работы ЭЭС.
Обобщенное уравнение состояния в матричной форме имеет вид:

где 



( 

Правило формирования: каждый элемент матрицы 


-1, если ветвь 


0, если ветвь 






-1, если направление ветки
противоположно направлению обхода контура


направлением обхода контура
0, если ветвь не входит в контур




При использовании обобщенного уравнения состояния расчет установившегося режима ЭЭС производится в следующем порядке: вначале определяются токи в ветвях схемы 



Общий вид уравнения узловых напряжений [1,2]:

где 




Для большинства реальных схем замещения нагрузка и генерация мощности моделируются с помощью задающих токов 


Матрица узловых проводимостей рассчитывается по формуле:



Структура 
- на главной диагонали расположены собственные проводимости узлов
 , равные сумме проводимостей ветвей, соединенных с узлом
, равные сумме проводимостей ветвей, соединенных с узлом  ; симметрично относительно главной диагонали расположены взаимные проводимости
; симметрично относительно главной диагонали расположены взаимные проводимости  (со знаком минус), которые равны проводимости ветви, находящейся между узлами
(со знаком минус), которые равны проводимости ветви, находящейся между узлами  и
и  , или нулю при отсутствии связи между узлами.
, или нулю при отсутствии связи между узлами.Матрица 
Использование уравнений узловых напряжений приводит к следующему порядку расчета режима ЭС: в начале определяются значения напряжений в узлах схемы 




Условие задачи: Для расчетной схемы, представленной на рис. 2.5 записать матричное уравнение узловых напряжений и рассчитать значения узловых напряжений методом Гаусса.


Расчет начинается с формирования уравнения состояния по расчетной схеме:
Составим матрицу инциденций 1-го рода.
При правильном составлении матрицы М строка, соответствующая балансирующему узлу, дополняет каждый столбец до нуля.
2.Составим транспонированную матрицу
3.Определяем матрицу узловых проводимостей
В матричной форме уравнение узловых напряжений имеет вид:

5. Перейдем к системе уравнений:

Далее, используя уравнения узловых напряжений, можно провести расчет установившегося режима в следующем порядке:
1. Решая систему уравнений вида (1.12), определяются значения узловых напряжений 
Прямой ход Гаусса состоит из однотипных шагов, связанных с формированием из матрицы коэффициентов 
Шаг 1. Получим первое ключевое уравнение, для чего разделим первое уравнение системы (2.5) на коэффициент при 


Шаг 2. Принимаем за ключевое второе уравнение (разделим все коэффициенты на 

Преобразованная система, начиная с ключевого уравнения имеет вид:

Шаг 3. Принимаем за ключевое третье уравнение и исключаем 

Шаг 4. Выбираем четвертое ключевое уравнение:

Обратный ход Гаусса:


Анализ точности расчета: Производится расчет невязок по исходной системе уравнений:

2. Из уравнения связи параметров режима [ 1 ] находятся падения напряжений в ветвях

3. Из уравнения закона Ома (1.1) определяются токи в ветвях схемы

4.По известным значениям 


Задана расчетная схема электрической системы, представленная в виде направленного графа, который содержит 5 узлов, 7 ветвей и 2 независимых контура (по вариантам в приложении). Направление ветвей и независимых контуров может быть задано произвольно. Для указанной схемы ЭС необходимо рассчитать параметры установившегося режима. В связи с этим, требуется выполнить следующие пункты задания:
1.Составить обобщенное уравнение состояния на основе первого и второго законов Кирхгофа, записать этого уравнение в матричной форме и в виде системы уравнений;
2.Вычислить матрицу узловых проводимостей 
3. Рассчитать узловые напряжения и токи в ветвях с использованием метода Гаусса с обратным ходом. Оценить точность полученных результатов. Исходные данные, необходимые для проведения расчетов, приведены в таблице 1 приложения
📸 Видео
Закон Ома для участка цепи. Электрическое сопротивление проводника. 8 класс.Скачать

Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать

Как составить уравнения по законам Кирхгофа?Скачать
Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Аналитическое определение решений уравнений состояния электрических цепей.Скачать

Метод контурных токов - определение токов. ЭлектротехникаСкачать

Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Решение задачи. Расчет электрической цепи по законам КирхгофаСкачать

Построение матриц электрических цепейСкачать

Электромеханические переходные процессы. Устойчивость. Уравнение движение ротора.Скачать
Что такое РЕЗОНАНС НАПРЯЖЕНИЙ | САМОЕ ПОНЯТНОЕ объяснениеСкачать

Математика это не ИсламСкачать

Лекция 122. Переходные процессыСкачать

СИСТЕМА УРАВНЕНИЙ ЭЛЕКТРИЧЕСКОГО РАВНОВЕСИЯСкачать

2020 г. Дифференциальные уравнения для электрических цепей. Лекция и практикаСкачать

Предельные вероятности состоянийСкачать