- Третье и четвертое уравнения Максвелла
- Тема: Уравнения Максвелла
- Уравнения Максвелла в интегральной форме.
- Теорема о циркуляции магнитного поля.
- Теорема Остроградского — Гаусса
- Поток вектора напряженности поля точечного заряда
- Теорема Остроградского — Гаусса в интегральной форме
- Теорема Остроградского — Гаусса в дифференциальной форме
- Готовые работы на аналогичную тему
- 💥 Видео
Видео:Билет №16 "Теорема о циркуляции и теорема Гаусса для магнитного поля"Скачать
Третье и четвертое уравнения Максвелла
Третье уравнение Максвелла является обобщением закона Гаусса на случай переменных процессов. Закон Гаусса связывает поток вектора электрического смещения через произвольную замкнутую поверхность S с зарядом Q, сосредоточенным внутри этой поверхности:
, (1.40)
где dS = n0dS; n0 – орт внешней нормали к поверхности S.
До Максвелла уравнение (1.40) рассматривалось только в применении к постоянным полям. Максвелл предположил, что оно справедливо и в случае переменных полей.
Заряд Q может быть произвольно распределен внутри поверхности S. Поэтому в общем случае
, (1.41)
где ρ – объемная плотность зарядов; V—объем, ограниченный поверхностью S. Объемная плотность зарядов
, (1.42)
где ΔQ – заряд, сосредоточенный в объеме ΔV. Размерность ρ – кулон на кубический метр (Кл/м3).
Подставляя (1.41) в (1.40), получаем
. (1.43)
Уравнение (1.43) обычно называют третьим уравнением Максвелла в интегральной форме. Для перехода к дифференциальной форме преобразуем левую часть этого уравнения по теореме Остроградского-Гаусса (П. 19). В результате получим:
.
Это равенство должно выполняться при произвольном объеме V, что возможно только в том случае, если
Соотношение (1.44) принято называть третьим уравнением Максвелла. В декартовой системе координат оно записывается в виде
.
Из равенства (1.44) следует, что дивергенция вектора D отлична от нуля в тех точках пространства, где имеются свободные заряды. В этих точках линии вектора D имеют начало (исток) или конец (сток). Линии вектора D начинаются на положительных зарядах и заканчиваются – на отрицательных.
В отличие от вектора D истоками (стоками) вектора Е могут быть как свободные, так и связанные заряды. Чтобы показать это, перепишем уравнение (1.44) для вектора Е. Подставляя соотношение (1.4) в (1.44), получаем εоdiv Е = ρ – div P. Второе слагаемое в правой части этого равенства имеет смысл объемной плотности зарядов 
, возникающих в результате неравномерной поляризации среды (такие заряды будем называть поляризационными):
divP = —. (1.45)
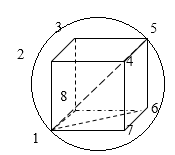
Поясним возникновение поляризационных зарядов на следующем примере. Пусть имеется поляризованная среда (рис. 1.8). Выделим мысленно внутри нее объем ΔV, ограниченный поверхностью ΔS. В результате поляризации в среде происходит смещение зарядов, связанных с молекулами вещества. Если объем ΔV мал, а поляризация неравномерная, то в объем ΔV с одной стороны может войти больше зарядов, чем выйдет с другой (на рис. 1.8 объем ΔVпоказан пунктиром). Подчеркнем, что поляризационные заряды являются «связанными» и возникают только под действием электрического поля. Знак минус в формуле (1.45) следует из определения вектора Р (см. 1.2.1).
Рис. 1.8. Поляризованная среда
Линии вектора Р начинаются на отрицательных зарядах и оканчиваются на положительных. С учетом формулы (1.45) приходим к соотношению εоdiv Е = ρ + ρp, из которого и следует сделанное выше утверждение, что истоками (стоками) линий вектора Е (силовых линий электрического поля) являются как свободные, так и связанные заряды.
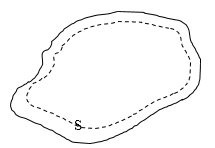
Четвертое уравнение Максвелла в интегральной форме совпадает с законом Гаусса для магнитного поля, который можно сформулировать следующим образом. Поток вектора В через любую замкнутую поверхность S равен нулю, т.е.
. (1.46)
Это означает, что не существует линий вектора В, которые только входят в замкнутую поверхность S (или, наоборот, только выходят из поверхности S): они всегда пронизывают ее (рис. 1.9).
Рис. 1.9. Линии вектора В, пронизывающие поверхность S
Уравнение (1.46) называют четвертым уравнением Максвелла в интегральной форме. К дифференциальной форме уравнения (1.46) можно перейти с помощью теоремы Остроградского-Гаусса так же, как это было сделано в случае третьего уравнения Максвелла. В результате получим
Уравнение (1.47) представляет собой четвертое уравнение Максвелла. Оно показывает, что в природе отсутствуют уединенные магнитные заряды одного знака. Из этого уравнения также следует, что линии вектора В (силовые линии магнитного поля) являются непрерывными.
Видео:Электростатика. Теорема Остроградского - ГауссаСкачать
Тема: Уравнения Максвелла
Тема: Уравнения Максвелла
Физический смысл уравнения Максвелла 
заключается в следующем
источником электрического поля являются свободные электрические заряды
Решение:
Данное уравнение Максвелла является обобщением теоремы Остроградского – Гаусса для электростатического поля в среде – источником электрического поля являются свободные электрические заряды. Максвелл предположил, что она справедлива для любого электрического поля, как стационарного, так и переменного.
Тема: Уравнения Максвелла
Утверждение «Переменное электрическое поле, наряду с электрическим током, является источником магнитного поля» раскрывает физический смысл уравнения …
Тема: Уравнения Максвелла
Физический смысл уравнения Максвелла заключается в следующем …
источником электрического поля являются свободные электрические заряды
изменяющееся со временем магнитное поле порождает вихревое электрическое поле
«магнитных зарядов» не существует: силовые линии магнитного поля замкнуты
источником вихревого магнитного поля, помимо токов проводимости, является изменяющееся со временем электрическое поле
Решение:
Данное уравнение Максвелла является обобщением теоремы Остроградского – Гаусса для электростатического поля в среде – источником электрического поля являются свободные электрические заряды. Максвелл предположил, что она справедлива для любого электрического поля, как стационарного, так и переменного.
Тема: Уравнения Максвелла
Физический смысл уравнения Максвелла заключается в следующем …
источником электрического поля являются свободные электрические заряды
Решение:
Данное уравнение Максвелла является обобщением теоремы Остроградского – Гаусса для электростатического поля в среде – источником электрического поля являются свободные электрические заряды. Максвелл предположил, что она справедлива для любого электрического поля, как стационарного, так и переменного.
Тема: Уравнения Максвелла
Физический смысл уравнения Максвелла заключается в следующем …
источником электрического поля являются свободные электрические заряды
Тема: Уравнения Максвелла
Физический смысл уравнения Максвелла заключается в следующем …
источником электрического поля являются свободные электрические заряды
Тема: Уравнения Максвелла
Обобщением теоремы Остроградского – Гаусса для электростатического поля в среде является уравнение …
Решение:
Уравнение Максвелла является обобщением теоремы Остроградского – Гаусса для электростатического поля в среде – источником электрического поля являются свободные электрические заряды. Максвелл предположил, что она справедлива для любого электрического поля, как стационарного, так и переменного.
Тема: Уравнения Максвелла
Физический смысл уравнения Максвелла заключается в следующем …
источником вихревого магнитного поля помимо токов проводимости является изменяющееся со временем электрическое поле
Тема: Уравнения Максвелла
Физический смысл уравнения Максвелла 
заключается в следующем …
«магнитных зарядов» не существует: силовые линии магнитного поля замкнуты
Решение:
Уравнение Максвелла означает, что в природе нет магнитных зарядов, на которых начинались бы или заканчивались линии магнитной индукции.
Тема: Уравнения Максвелла
Утверждение «Переменное электрическое поле, наряду с электрическим током, является источником магнитного поля» раскрывает физический смысл уравнения …
Решение:
Из уравнения следует, что источником вихревого магнитного поля являются токи проводимости и переменное электрическое поле, для которого 
.
Тема: Уравнения Максвелла
Полная система уравнений Максвелла для электромагнитного поля в интегральной форме имеет вид:
,,,
0.
Следующая система уравнений:,
,
,
0 –
справедлива для …
электромагнитного поля в отсутствие свободных зарядов
Решение:
Вторая система уравнений отличается от первой системы своими вторым и третьим уравнениями. Во втором уравнении иначе записано подынтегральное выражение, но 
. В третьем уравнении отсутствует плотность 
свободных зарядов. Следовательно, рассматриваемая система справедлива для электромагнитного поля в отсутствие свободных зарядов.
Тема: Уравнения Максвелла
Уравнения Максвелла являются основными законами классической макроскопической электродинамики, сформулированными на основе обобщения важнейших законов электростатики и электромагнетизма. Эти уравнения в интегральной форме имеют вид:
1).
;
2).;
3).;
4). 0.
Третье уравнение Максвелла является обобщением …
теоремы Остроградского – Гаусса для электростатического поля в среде
Решение:
Третье уравнение Максвелла является обобщением теоремы Остроградского – Гаусса для электростатического поля в среде. Максвелл предположил, что она справедлива для любого электрического поля, как стационарного, так и переменного.
Тема: Уравнения Максвелла
Физический смысл уравнения Максвелла заключается в следующем …
источником электрического поля являются свободные электрические заряды
Тема: Уравнения Максвелла
Физический смысл уравнения Максвелла заключается в следующем …
источником вихревого магнитного поля помимо токов проводимости является изменяющееся со временем электрическое поле
Тема: Уравнения Максвелла
Полная система уравнений Максвелла для электромагнитного поля в интегральной форме имеет вид:,,,
0.
Следующая система уравнений:
,
,,
0 –
справедлива для …
электромагнитного поля при наличии заряженных тел и в отсутствие токов проводимости
Тема: Уравнения Максвелла
Утверждение «Переменное электрическое поле, наряду с электрическим током, является источником магнитного поля» раскрывает физический смысл уравнения …
Решение:
Из уравнения следует, что источником вихревого магнитного поля являются токи проводимости и переменное электрическое поле, для которого .
Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать
Уравнения Максвелла в интегральной форме.
Физический смысл этого выражения таков: поток электрической индукции (D) через произвольную замкнутую поверхность s равен суммарному заряду, заключенному внутри этой поверхности (q). Заметим, что похожее выражение мы уже встречали, когда говорили о теореме Остроградского — Гаусса для электрических полей (6.4).
Видео:Билет №02 "Теорема Гаусса"Скачать
Теорема о циркуляции магнитного поля.
Выражение фI)ds = у, продифференцируем по времени. Получим
Если поверхность s не деформируется, то справедливо
Далее вводится понятие тока смещения (/ol) и плотности тока смещения 0′сн = dlcjdt). Ток смещения — это физическая величина, равная потоку вектора плотности тока смещения (jm) сквозь поверхность .v, он является источником вихревого магнитного поля. Можно сказать, что ток смещения — физическая величина, прямо пропорциональная скорости изменения электрической индукции. Строго говоря, ток смещения не является электрическим током, но измеряется в тех же единицах, что и электрический ток.
В природе можно выделить два вида токов: ток связанных зарядов и ток проводимости. Ток связанных зарядов — это перемещение средних положений связанных электронов и ядер, составляющих молекулу, относительно центра молекулы. Ток проводимости — это направленное движение зарядов на большие расстояния. Сумма тока связанных зарядов и быстроты изменения потока электрического поля была названа током смещения.
Считая, что ток смещения
и воспользовавшись законом полного тока (6.20), можно записать следующее уравнение Максвелла 
Видео:54. Магнитный поток. Теорема ГауссаСкачать
Теорема Остроградского — Гаусса
Вы будете перенаправлены на Автор24
Видео:Электрическое поле. Теорема ГауссаСкачать
Поток вектора напряженности поля точечного заряда
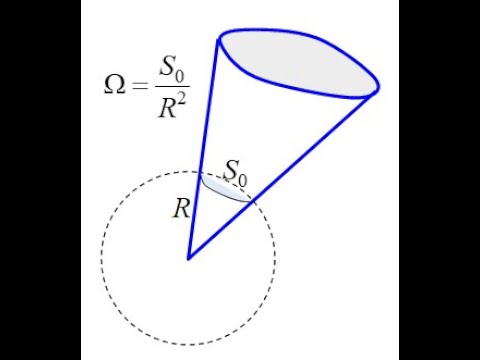
Рассмотрим поле точечного заряда $q$, найдем поток вектора напряжённости ($overrightarrow$) через замкнутую поверхность $S$. Будем считать, что заряд находится внутри поверхности. Поток вектора напряженности через любую поверхность равен количеству линий вектора напряженности, которые выходят наружу (начинаются на заряде, если $q>0$) или количеству линий $overrightarrow$входящих внутрь, если $q [Ф_E=frac<_0> left(1right),]
где знак потока совпадает со знаком заряда.
Видео:Урок 223. Теорема ГауссаСкачать
Теорема Остроградского — Гаусса в интегральной форме
Допустим, что внутри поверхности S находится N точечных зарядов, величины $q_1,q_2,dots q_N.$ Из принципа суперпозиции мы знаем, что результирующая напряженность поля всех N зарядов может быть найдена как сумма напряженностей полей, которые создаются каждым из зарядов, то есть:
Следовательно, для потока системы точечных зарядов можно записать:
Используем формулу (1), получаем, что:
Уравнение (4) значит, что поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме зарядов, которые находятся внутри данной поверхности, деленой на электрическую постоянную. Это теорема Остроградского — Гаусса в интегральной форме. Данная теорема является следствием закона Кулона. Значение данной теоремы заключается в том, что она позволяет довольно просто вычислять электрические поля при различных распределениях зарядов.
Как следствие теоремы Остроградского — Гаусса надо сказать, что поток вектора напряженности ($Ф_E$) через замкнутую поверхность в случае при котором заряды находятся вне данной поверхности, равен нулю.
В том случае, когда можно не учитывать дискретность зарядов используют понятие объемной плотности заряда ($rho $), если заряд распределен по объему. Она определена как:
где $dq$ — заряд, который можно считать точечным, $dV$ — малый объем. (Относительно $dV$ необходимо сделать следующее замечание. Данный объем мал настолько, чтобы плотность заряда в нем можно было считать постоянной, но достаточно велик, чтобы не начала проявляться дискретность заряда). Суммарный заряд, который находится в полости, можно найти как:
В таком случае формулу (4) перепишем в виде:
Видео:Применение теоремы Гаусса-Остроградского. Напряжённость поля пластины, сферы и шара.Скачать
Теорема Остроградского — Гаусса в дифференциальной форме
Используя формулу Остроградского — Гаусса для любого поля векторной природы, с помощью которой осуществляется переход от интегрирования по замкнутой поверхности к интегрированию по объему:
Равенства в уравнении (9) выполняются для любого объема, а это осуществимо только, если функции, которые находятся в подынтегральных выражениях, равны в каждой токе пространства, то есть мы можем записать, что:
Готовые работы на аналогичную тему
Выражение (10) — теорема Остроградского — Гаусса в дифференциальной форме. Трактовка ее такова: заряды являются источниками электрического поля. Если $divoverrightarrow>0$, то в этих точках поля (заряды положительные) мы имеем источники поля, если $divoverrightarrow
Задание: Заряд равномерно распределен по объему, в этом объеме выделена кубическая поверхность, со стороной b. Она вписана в сферу. Найдите отношение потоков вектора напряженности сквозь эти поверхности.
Согласно теореме Гаусса поток ($Ф_E$) вектора напряженности $overrightarrow$ через замкнутую поверхность при равномерном распределении заряда по объему равен:
Следовательно, нам необходимо определить объемы куба и шара, если шар описать вокруг этого куба. Для начала, объем куба ($V_k$) если сторона его b равен:
Найдем объем шара ($V_$) по формуле:
где $D$ — диаметр шара и (так как шар описан вокруг куба), главная диагональ куба. Следовательно, нам необходимо выразить диагональ куба через его сторону. Это легко сделать, если использовать теорему Пифагора. Для вычисления диагонали куба, например, (1,5) нам сначала необходимо найти диагональ квадрата (нижнего основания куба) (1,6). Длина диагонали (1,6) равна:
В таком случает длина диагонали (1,5) равна:
Подставим в (1.3) найденный диаметр шара, получим:
Теперь мы можем найти потоки вектора напряженности через поверхность куба, она равна:
через поверхность шара:
Ответ: Поток через поверхность шара в 2,7 раза больше.
Задание: Докажите, что заряд проводника располагается на его поверхности.
Используем для доказательства теорему Гаусса. Выделим в проводнике замкнутую поверхность произвольной формы около поверхности проводника (рис.2).
Допустим, что заряды внутри проводника есть, запишем с теорему Остроградского — Гаусса для дивергенции поля имеем для любой точки поверхности S:
где $rho -плотность $внутреннего заряда. Однако поля внутри проводника нет, то есть $overrightarrow=0$, следовательно, $divoverrightarrow=0to rho =0$. Теорема Остроградского — Гаусса в дифференциальной форме локальна, то есть, она записана для точки поля, мы специальным образом точку не выбирали, следовательно, плотность заряда равна нулю в любой точке поля внутри проводника.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 03.12.2021
💥 Видео
Теорема Гаусса - доказательство.Скачать
43. Применение теоремы ГауссаСкачать
Примеры применения теоремы Гаусса 2021 1Скачать
Электростатика | закон Гаусса для электрического поля | 1Скачать
Теорема Гаусса для расчета полей цилиндра (нити) и плоскостиСкачать
Формула Остроградского-ГауссаСкачать
2.10. Система уравнений электромагнитного поляСкачать
42. Теорема Гаусса. Расчет электростатических полейСкачать
Лекция 4-4 Теорема Гаусса в дифференциальной формеСкачать
Поток вектора напряженности электрического поля. Теорема Гаусса. Практическая часть. 10 класс.Скачать
Введение в теорию электромагнитного поля. Первое уравнение Максвелла.Скачать
Лекция 2.1. Теорема ГауссаСкачать
