Область значений для квадратного уравнения

Любое выражение с переменной имеет свою область допустимых значений, где оно существует. ОДЗ необходимо всегда учитывать при решении. При его отсутствии можно получить неверный результат.

В данной статье будет показано, как правильно находить ОДЗ, использовать на примерах. Также будет рассмотрена важность указания ОДЗ при решении.

Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Допустимые и недопустимые значения переменных

Данное определение связано с допустимыми значениями переменной. При введении определения посмотрим, к какому результату приведет.

Начиная с 7 класса, мы начинаем работать с числами и числовыми выражениями. Начальные определения с переменными переходят к значению выражений с выбранными переменными.

Когда имеются выражения с выбранными переменными, то некоторые из них могут не удовлетворять. Например, выражение вида 1 : а , если а = 0 , тогда оно не имеет смысла, так как делить на ноль нельзя. То есть выражение должно иметь такие значения, которые подойдут в любом случае и дадут ответ. Иначе говоря, имеют смысл с имеющимися переменными.

Если имеется выражение с переменными, то оно имеет смысл только тогда, когда при их подстановке значение может быть вычислено.

Если имеется выражение с переменными, то оно не имеет смысл, когда при их подстановке значение не может быть вычислено.

То есть отсюда следует полное определение

Существующими допустимыми переменными называют такие значения, при которых выражение имеет смысл. А если смысла не имеет, значит они считаются недопустимыми.

Для уточнения вышесказанного: если переменных более одной, тогда может быть и пара подходящих значений.

Для примера рассмотрим выражение вида 1 x — y + z , где имеются три переменные. Иначе можно записать, как x = 0 , y = 1 , z = 2 , другая же запись имеет вид ( 0 , 1 , 2 ) . Данные значения называют допустимыми, значит, можно найти значение выражения. Получим, что 1 0 — 1 + 2 = 1 1 = 1 . Отсюда видим, что ( 1 , 1 , 2 ) недопустимы. Подстановка дает в результате деление на ноль, то есть 1 1 — 2 + 1 = 1 0 .

Видео:Функция. Область определения функции. Практическая часть. 10 класс.Скачать

Что такое ОДЗ?

Область допустимых значений – важный элемент при вычислении алгебраических выражений. Поэтому стоит обратить на это внимание при расчетах.

Область ОДЗ – это множество значений, допустимых для данного выражения.

Рассмотрим на примере выражения.

Если имеем выражение вида 5 z — 3 , тогда ОДЗ имеет вид ( − ∞ , 3 ) ∪ ( 3 , + ∞ ) . Эта область допустимых значений, удовлетворяющая переменной z для заданного выражения.

Если имеется выражения вида z x — y , тогда видно, что x ≠ y , z принимает любое значение. Это и называют ОДЗ выражения. Его необходимо учитывать, чтобы не получить при подстановке деление на ноль.

Область допустимых значений и область определения имеет один и тот же смысл. Только второй из них используется для выражений, а первый – для уравнений или неравенств. При помощи ОДЗ выражение или неравенство имеет смысл. Область определения функции совпадает с областью допустимых значений переменной х к выражению f ( x ) .

Видео:Квадратичная функция: область значений, убывание/возрастание функцииСкачать

Как найти ОДЗ? Примеры, решения

Найти ОДЗ означает найти все допустимые значения, подходящие для заданной функции или неравенства. При невыполнении этих условий можно получить неверный результат. Для нахождения ОДЗ зачастую необходимо пройти через преобразования в заданном выражении.

Существуют выражения, где их вычисление невозможно:

• если имеется деление на ноль;
• извлечение корня из отрицательного числа;
• наличие отрицательного целого показателя – только для положительных чисел;
• вычисление логарифма отрицательного числа;
• область определения тангенса π 2 + π · k , k ∈ Z и котангенса π · k , k ∈ Z ;
• нахождение значения арксинуса и арккосинуса числа при значении, не принадлежащем [ — 1 ; 1 ] .

Все это говорит о том, как важно наличие ОДЗ.

Найти ОДЗ выражения x 3 + 2 · x · y − 4 .

Решение

В куб можно возводить любое число. Данное выражение не имеет дроби, поэтому значения x и у могут быть любыми. То есть ОДЗ – это любое число.

Ответ: x и y – любые значения.

Найти ОДЗ выражения 1 3 — x + 1 0 .

Решение

Видно, что имеется одна дробь, где в знаменателе ноль. Это говорит о том, что при любом значении х мы получим деление на ноль. Значит, можно сделать вывод о том, что это выражение считается неопределенным, то есть не имеет ОДЗ.

Ответ: ∅ .

Найти ОДЗ заданного выражения x + 2 · y + 3 — 5 · x .

Решение

Наличие квадратного корня говорит о том, что это выражение обязательно должно быть больше или равно нулю. При отрицательном значении оно не имеет смысла. Значит, необходимо записать неравенство вида x + 2 · y + 3 ≥ 0 . То есть это и есть искомая область допустимых значений.

Ответ: множество x и y , где x + 2 · y + 3 ≥ 0 .

Определить ОДЗ выражения вида 1 x + 1 — 1 + log x + 8 ( x 2 + 3 ) .

Решение

По условию имеем дробь, поэтому ее знаменатель не должен равняться нулю. Получаем, что x + 1 — 1 ≠ 0 . Подкоренное выражение всегда имеет смысл, когда больше или равно нулю, то есть x + 1 ≥ 0 . Так как имеет логарифм, то его выражение должно быть строго положительным, то есть x 2 + 3 > 0 . Основание логарифма также должно иметь положительное значение и отличное от 1 , тогда добавляем еще условия x + 8 > 0 и x + 8 ≠ 1 . Отсюда следует, что искомое ОДЗ примет вид:

x + 1 — 1 ≠ 0 , x + 1 ≥ 0 , x 2 + 3 > 0 , x + 8 > 0 , x + 8 ≠ 1

Иначе говоря, называют системой неравенств с одной переменной. Решение приведет к такой записи ОДЗ [ − 1 , 0 ) ∪ ( 0 , + ∞ ) .

Ответ: [ − 1 , 0 ) ∪ ( 0 , + ∞ )

Видео:Функция. Область определения и область значений функцииСкачать

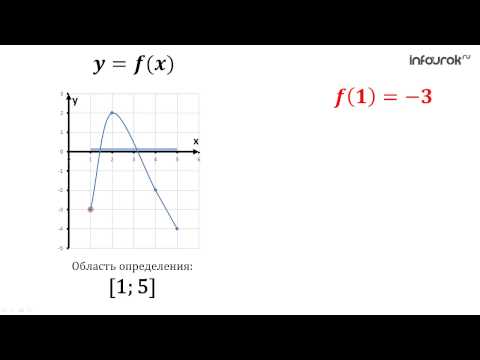
Почему важно учитывать ОДЗ при проведении преобразований?

При тождественных преобразованиях важно находить ОДЗ. Бывают случаи, когда существование ОДЗ не имеет место. Чтобы понять, имеет ли решение заданное выражение, нужно сравнить ОДЗ переменных исходного выражения и ОДЗ полученного.

• могут не влиять на ОДЗ;
• могут привести в расширению или дополнению ОДЗ;
• могут сузить ОДЗ.

Рассмотрим на примере.

Если имеем выражение вида x 2 + x + 3 · x , тогда его ОДЗ определено на всей области определения. Даже при приведении подобных слагаемых и упрощении выражения ОДЗ не меняется.

Если взять пример выражения x + 3 x − 3 x , то дела обстоят иначе. У нас имеется дробное выражение. А мы знаем, что деление на ноль недопустимо. Тогда ОДЗ имеет вид ( − ∞ , 0 ) ∪ ( 0 , + ∞ ) . Видно, что ноль не является решением, поэтому добавляем его с круглой скобкой.

Рассмотрим пример с наличием подкоренного выражения.

Если имеется x — 1 · x — 3 , тогда следует обратить внимание на ОДЗ, так как его необходимо записать в виде неравенства ( x − 1 ) · ( x − 3 ) ≥ 0 . Возможно решение методом интервалов, тогда получаем, что ОДЗ примет вид ( − ∞ , 1 ] ∪ [ 3 , + ∞ ) . После преобразования x — 1 · x — 3 и применения свойства корней имеем, что ОДЗ можно дополнить и записать все в виде системы неравенства вида x — 1 ≥ 0 , x — 3 ≥ 0 . При ее решении получаем, что [ 3 , + ∞ ) . Значит, ОДЗ полностью записывается так: ( − ∞ , 1 ] ∪ [ 3 , + ∞ ) .

Нужно избегать преобразований, которые сужают ОДЗ.

Рассмотрим пример выражения x — 1 · x — 3 , когда х = — 1 . При подстановке получим, что — 1 — 1 · — 1 — 3 = 8 = 2 2 . Если это выражение преобразовать и привести к виду x — 1 · x — 3 , тогда при вычислении получим, что 2 — 1 · 2 — 3 выражение смысла не имеет, так как подкоренное выражение не должно быть отрицательным.

Следует придерживаться тождественных преобразований, которые ОДЗ не изменят.

Если имеются примеры, которые его расширяют, тогда его нужно добавлять в ОДЗ.

Рассмотрим на примере дроби вида x x 3 + x . Если сократить на x , тогда получаем, что 1 x 2 + 1 . Тогда ОДЗ расширяется и становится ( − ∞ 0 ) ∪ ( 0 , + ∞ ) . Причем при вычислении уже работаем со второй упрощенной дробью.

При наличии логарифмов дело обстоит немного иначе.

Если имеется выражение вида ln x + ln ( x + 3 ) , его заменяют на ln ( x · ( x + 3 ) ) , опираясь на свойство логарифма. Отсюда видно, что ОДЗ с ( 0 , + ∞ ) до ( − ∞ , − 3 ) ∪ ( 0 , + ∞ ) . Поэтому для определения ОДЗ ln ( x · ( x + 3 ) ) необходимо производить вычисления на ОДЗ, то есть ( 0 , + ∞ ) множества.

При решении всегда необходимо обращать внимание на структуру и вид данного по условию выражения. При правильном нахождении области определения результат будет положительным.

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Квадратичная функция. Построение параболы

О чем эта статья:

8 класс, 9 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:9 класс, 15 урок, Определение числовой функции. Область определения, область значения функцииСкачать

Основные понятия

Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ: наглядно.

• Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

График функции — это объединение всех точек, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.

Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Построение квадратичной функции

Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:

График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :

Точки, обозначенные зелеными кружками называют базовыми точками. Чтобы найти их координаты для функции y = x 2 , нужно составить таблицу:

x

y

Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.

График функции y = –x 2 выглядит, как перевернутая парабола:

Зафиксируем координаты базовых точек в таблице:

x

y

Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:

• Если старший коэффициент больше нуля a > 0, то ветви параболы напрaвлены вверх.
• Если старший коэффициент меньше нуля a 2 + bx + c, для построения которой нужно решить квадратное уравнение ax 2 + bx + c = 0. В процессе найдем дискриминант D = b 2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.

Рассмотрим три случая:

1. Если D 0,то график выглядит так:

1. Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
2. Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:

Если a > 0, то график выглядит как-то так:

0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>

На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.

Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:

Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.

Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).

На изображении отмечены основные параметры графика квадратичной функции:

Видео:Алгебра 9 класс. Область определения функцииСкачать

Алгоритм построения параболы

Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.

Видео:Функция. Множество значений функции. Практическая часть. 10 класс.Скачать

Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.

Разберем общий алгоритм на примере y = 2x 2 + 3x — 5.

Как строим:

1. Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
2. Найдем дискриминант квадратного трехчлена 2x 2 + 3x — 5.

D = b 2 — 4ac = 9 — 4 * 2 * (-5) = 49 > 0

В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:

2x 2 + 3x — 5 = 0 2 + 3x — 5 = 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAPoAAAAyCAYAAAB1V8bkAAAJyElEQVR4Ae2c16sUwRLGfdRX/wXFB30QFFQUQUyIKCIGBEEQzCCoKIgB01ExZwVz4JpzztljwJxzzjlnrcuvL33unD2zOzO7OzvuThU0u5N6uuvrr7u6unrKiYpqQDVQ8BooV/A11AqqBlQDokTXRqAaiIEGlOgxAFmrqBpQomsbUA3EQANK9BiArFVUDSjRtQ2oBmKgASV6DEDWKqoGlOjaBlQDMdBAQRH9z58/8vv3b5P+/v2bMXy/fv0S8kxMGWesGRgNpIMXz7jhkg28CxmWgiH69+/f5dSpU7JixQpZtmyZXLx4UX7+/JkUOxoGjSaVTJw4UVatWiUbNmwoSYcPH071iF7zqYGgeNlsT58+LZMnTy7BA2y2bNkib9++tbfor4sGCobogD19+nR5/fq1nDx5Upo0aSLHjh2TZD39x48f5ebNmy4q+d8pRo327dtLo0aNTF6NGzeWevXqCeRXyVwDQfHijXTMmzZtMjiAL6lu3brSuXNnuXfvXuaFKuAcCobojOQDBgwwgD948EAg5ubNm42Z54bfjRs3ZMqUKW6XzDk6jP379wsjD/LmzRtZt26dvHr1KukzesG/BoLiRc5gceXKFZM4/vbtmxw6dEguXbokP3788P/yGN5ZMET/8uWLvHv3Tt6/f2/Muh49esj169eTQupF9MQHIfm1a9cST+txmhoIipfba86fPy9Hjx4VrDOV1BooGKJTTYh++fJlGTt2rCxevNgcJ6t+EKIz3587d26yrPR8mhoIglfiK549e2Y6dHBU8dZA3hH9+PHjYhNmnFO+fv1qTOwDBw5Ily5dhF+nQ47ndu/ebdLChQule/fuJcecp9E477d5d+zYUW7fvm0P9TeABixW/AbBCz+LffbChQtl3rh69WpZsmSJjuZlNON+Iu+IDkGZW+N427Ztm6nVp0+f5MiRI6Zh2Dl1hw4dZOjQoaVGdebc1oM+a9Ys48Sxx/y6zfUePnwoVapUcdeenvXUQLp4LV261OA8bdo0g5nzRR8+fJBhw4YJeav400DeEf3Ro0dmZGD+/fLlS1NLzLjhw4fLmDFjhEaA4DHv16+fGeHdVOHXdKczqVy5slsWes6HBtLF6/HjxwZn/CLPnz8v9aZbt25Jt27dlOiltJL6IO+I7lYdTPY1a9bIjBkz5M6dO7Jjxw5hRN++fXtSb6xfos+ZM0cqVark9trQzrEmXFxc7LnOH1oBQs44HbycRTpz5oy0a9funyA6DkGW/NavX19mauIsc+J/OkCmJliRL168ME7FVM7jxOeDHhcE0ak05KD3P3v2rFkWO3HihHz+/DmpPlh3XbRoUdLr9gL5LF++3B6G+nv//n3ZuHGjDBw4UDp16pS0kwq1EDnKPChezmI9efJEtm7dmnJVxXl/WP8PHjxopoxXr141RG3Tpo0JsPLzPqaaLVq0kDp16kjDhg2lb9++JgbEz7Pp3FMwRKfyBLkwX2fpxivqjbm8Nf1TKY77WK/NhVBuGvGoUaNMHID1N+Ti3VG8IwhezvIR5gwm/EYlrBgMGTJE9u3bZxy4YDV69Gjf/py9e/fKypUrjSVKLEDYqwcFRfSoQM/2e2fOnGmivgqd6NnWWy7zI3CqefPmUlRUVOIXgrzly5cXfEZewr2Y/XTuyaI3vfIIcj1tolM4lpyIBZ83b56MGzdO9uzZY0YjwkSfPn0apBx6r0MDYRBd8XIoOAt/sRiZU0N4az2OHz9eKlSo4MvSgOgs6RKIBYdIYUraRMfsYpkL84m5cc+ePY1DYv78+dKnTx/B2eAlmKldu3b1TISy5luII8s/XnWbNGmSMC9PlDCIrniJcXB6YcJ15s9+JHEkrlq1qixYsMDPowLRcRqzSgSHiOkI0xeUNtHpxXBUIQQ3tGrVKnLniC8N58FNYRBd8QoOPES2Php8Agw2dvR25gZRcaaNHDnSeTrlf/JxdhTsuMQacJ5LmUHAi2kT3b6HyrNBoXXr1uYUBXVThr3f+YuCcGp4JZRsFYAV8K8lt1hremqveuE4RAeJEgbR7Tvigpfb1JG6e2HCde5DCJbCM16rVi2T2D9BiLVT6Agwv3GsgSXPumHqfAZ+sLqCNWfbNQ455ve8MwxJm+gsXeF0YFcXPRlRaAiebD/OCO5l/XDQoEGeCTPHhqZWq1ZN/rVElF2iTJ061bNemHkEhiRKGESPG141atRIVKtZevXT3tjz7kcYgIioZDRmtyM6Zk09sf0zbYIndkBgabFt27ZmeZeYAgQzvmLFimWe9VMOP/ekTXTWMXv37m16uF69esmECRNMZdgDzgcgVIJrwLm8Vr9+fSECjM4wG6J4ZUOL/8+DgQdSwwGccIRkk4jITBRGaZZM8V/ZlRRGdIJlwJzBsX///gKPwpK0iY7HkArSgKgwu8XYMnju3LmkgSr0ZNZUCatCfvLFtKIHtj2sn2dycY8NmCGcF6cQIwXx+dmQfMMLfEj/qjA1Yx29ZcuWpRLmfaLcvXtXBg8eLCNGjChxUoM1mBAdt3btWmP9ZatTT3w/x2kTHcKytAB5EeYmyYiDecpWz9mzZyf9EIRb4cI6Rw/KikGcLI98w4vlWkKYC0Uw5xkEMeGt4A/Akc28P+wBMG2i28L6+WV7IruRmjVrVmK6+HkujHuYL+3atcuUhbm/SlkNRI0Xn/iqWbOmaTNlS5d/ZzDzITOhslFJTohO5Rg98WDaOUoUFabXpBExV2JThBI9OQpR4YX1x3SQb/UxOBSCYO2yA48RPCqJFdGZmxN8w/q/Ej11k4uK6ERXMqflw4+FQvTUms7N1VgRnYgndq2RlOipG1gURCf2myhLpldNmzZVoqeGKNDV2BAdj+bOnTuNcpTo3m0k10THrCVohCAiRInujVGQO2JDdJYA8bQTpIJHt3bt2mZtk1FEpawGck10PrRB4BEf4QQjgqIIK2UbqErmGsgJ0fE2AmL16tWFj/oRwpprYcRgVCcR+URsPkELBCyolNZAFHgRVcZyrcWoQYMGwtd97KfBSpdQj4JqICdEZ3kBkwwQIZZXLHDQSvi9H687G/wJgyREkl+7McdvHnG4L0q8WG9mUOCDnASf4DxVyVwDOSF65sXMXg6QnYbMMh+/fjfgZK8EmlMqDYAPzji7WyyqQSFVGfPxWuyIno8gaZlVA5lqQImeqQb1edVAHmhAiZ4HIGkRVQOZakCJnqkGI3m+WIrKlZOi45G8XF+ahxpQouchaKbIx4uU6PmKXQTlVqJHoPTMX/lM/tOuSIozz0hziIkGlOgxAVqrGW8NKNHjjb/WPiYaUKLHBGitZrw1oESPN/5a+5hoQIkeE6C1mvHWwH8BSUfSiO3XWNEAAAAASUVORK5CYII=»>

1. Координаты вершины параболы:

1. Точка пересечения с осью OY находится: (0; -5) и ей симметричная.
2. Нанести эти точки на координатную плоскость и построить график параболы:
   2 + 3x — 5 = 0″ height=»671″ src=»https://lh6.googleusercontent.com/TYyA5dFfh0ZKINaPSps3Y_X1mCv8Mhv_8bNG3_dPbZud1AEsvo7UBFmVQNm1GcR1CQFo6HE1lNjYaAgepQUTQiK_ay_Fnuv7LEsB53woHkFO66W0R1PP8QfGsFcYzaR_h4AJdLxC» width=»602″>

Видео:Исследование квадратичной функции. 8 класс.Скачать

Уравнение квадратичной функции имеет вид y = a * (x — x₀) 2 + y₀

Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x 2 + 3x — 5 при а = 1, то второй коэффициент является четным числом.

Рассмотрим пример: y = 2 * (x — 1) 2 + 4.

Как строим:

1. Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:

• построить y = x 2 ,
• умножить ординаты всех точек графика на 2,
• сдвинуть его вдоль оси ОХ на 1 единицу вправо,
• сдвинуть его вдоль оси OY на 4 единицы вверх.

1. Построить график параболы для каждого случая. 2 + y₀» height=»431″ src=»https://lh5.googleusercontent.com/_zgF-CXWf4Yy0p2OnBYSJkUm0zO-mNetq5feU6LIPEbIgSrO9kdr2ti_tr7Gg3yTMOlJVnuZgG0HleAFfAzG7yr7ELHT6KSMqMrRHkHqt-VcgIiSZx80cVj0zlPMBzEM0wAWQ-L6″ width=»602″>

Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)

Рассмотрим следующий пример: y = (x − 2) × (x + 1).

Как строим:

Данный вид уравнения позволяет быстро найти нули функции:

(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.

Определим координаты вершины параболы:

Найти точку пересечения с осью OY:

с = ab = (−2) × (1) = −2 и ей симметричная.

Отметим эти точки на координатной плоскости и соединим плавной прямой.

Видео:Область значений функцииСкачать

Практика. Функции. Часть 1. Область определения и область значений функции

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На предыдущих уроках мы познакомились с базовыми функциями, их свойствами и графиками. Кроме того, узнали о различных преобразованиях графиков функций. На этом уроке мы разберем практические задания с функциями и их графиками, а также изучим еще один вид преобразования графиков функций.

📽️ Видео

Функция. Область определения и область значения функции. Алгебра, 9 классСкачать

Область определения (корня) функции #2. Алгебра 10 класс.Скачать

Функции. Урок №4. Область значений функции.Скачать

Область определения функции - 25 функций в одном видеоСкачать

Область допустимых значений. ОДЗ в выражении.Скачать

ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ - Алгебра 7 класс - Теория функцийСкачать

Область определения и область значений функции | Алгебра 10 класс #2 | ИнфоурокСкачать

Область определения функцийСкачать