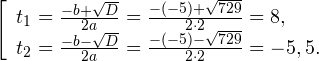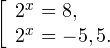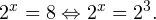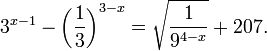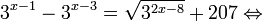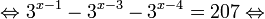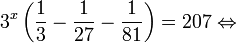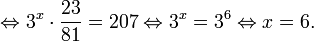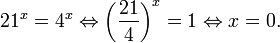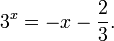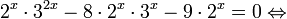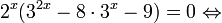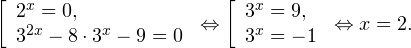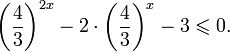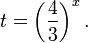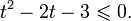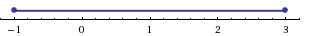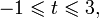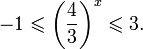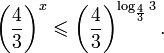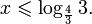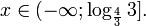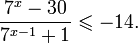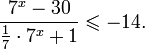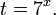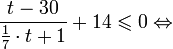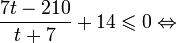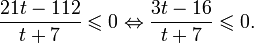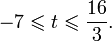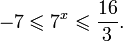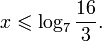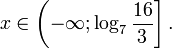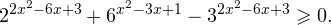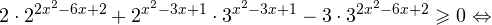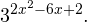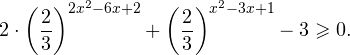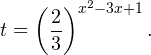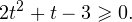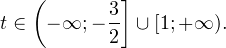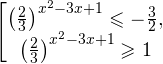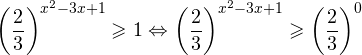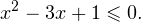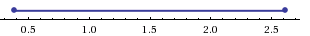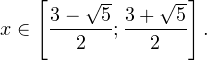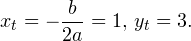О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
- Понятие области определения функции
- Материал со звездочкой
- Области определения основных элементарных функций
- Область определения постоянной функции
- Область определения функции с корнем
- Пример
- Область определения степенной функции
- Область определения показательной функции
- Область определения логарифмической функции
- Пример
- Область определения тригонометрических функций
- Пример
- Область определения обратных тригонометрических функций
- Таблица областей определения функций
- Показательные уравнения и неравенства с примерами решения
- Решении показательных уравнений
- Показательные уравнения и их системы
- Пример №1
- Пример №2
- Пример №3
- Пример №4
- Пример №5
- Пример №6
- Системы простейших показательных уравнений
- Пример №7
- Пример №8
- Пример №9
- Приближенное решение уравнений
- Пример №10
- Нахождение приближенного корня с заданной точностью
- Пример №11
- Показательные уравнения и неравенства
- Показательная функция
- Что такое показательная функция?
- Решение показательных неравенств
- 💡 Видео
Видео:Функция. Область определения функции. Практическая часть. 10 класс.Скачать

Понятие области определения функции
Впервые школьники знакомятся с термином «функция» на алгебре в 7 классе, и с каждой четвертью, с каждой новой темой это понятие раскрывается с новых сторон. И, конечно же, усложняются задачки. Сейчас дадим определения ключевым словам и будем находить область определения функции заданной формулой и по графику.
Если каждому значению x из некоторого множества соответствует число y, значит, на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у — зависимой переменной или функцией.
Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают так: y = f(x).
Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества.
Из понятия функции сформулируем определение области определения функции.
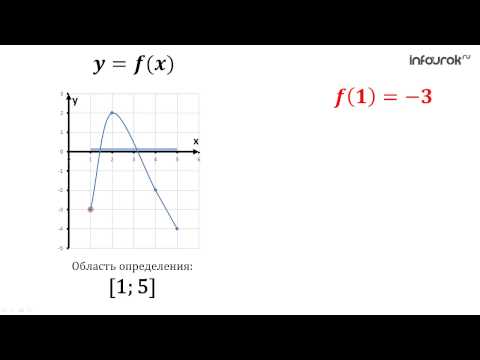
Область определения функции — это множество всех значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох. Чтобы обозначить область определения некоторой функции y, используют запись D(y).
Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.
- Например, область значений функции y = x2 — это все числа больше либо равные нулю. Это можно записать так: Е (у): у ≥ 0.
Материал со звездочкой
Старшеклассникам нужно помнить, что у некоторых функций есть собственные обозначения. Например, у тригонометрических. Поэтому в учебниках можно встретить такие записи: D(sin) — область определения функции синус, D(arcsin) — область определения функции арксинус.
Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = X. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) = [-1, 1].
Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.
Если мы хотим указать на множество чисел, которые лежат в некотором промежутке, то делаем так:
- Через точку с запятой указываем два числа: левую и правую границы промежутка.
- Если граница входит в промежуток, ставим возле нее квадратную скобку, если не входит — круглую.
- Если у промежутка нет правой границы, записываем так: ∞ или +∞. Если нет левой границы, пишем -∞.
- Если нужно описать множество, состоящее из нескольких промежутков, ставим между ними знак объединения: ∪.
Например, все действительные числа от 2 до 5 включительно можно записать так:
Все положительные числа можно описать так:
Ноль не положительное число, поэтому скобка возле него круглая.
Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Области определения основных элементарных функций
Область определения функции — неотъемлемая часть самой функции. Когда мы вводим какую-либо функцию, то сразу указываем ее область определения.
На уроках алгебры мы последовательно знакомимся с каждой функцией: прямая пропорциональность, линейная функция, функция y = x2 и другие. А области их определения изучаем, как свойства.
Рассмотрим области определения основных элементарных функций.
Видео:Показательные уравнения. 11 класс.Скачать

Область определения постоянной функции
Постоянная функция задается формулой y = C, то есть f(x) = C, где C — некоторое действительное число. Ее еще называют константа.
Смысл функции — в том, что каждому значению аргумента соответствует значение функции, которое равно C. Поэтому, область определения этой функции — множество всех действительных чисел R.
- Область определения постоянной функции y = -3 — это множество всех действительных чисел: D(y) = (−∞, +∞) или D(y) = R.
- Областью определения функции y = 3 √9 является множество R.
Еще больше наглядных примеров и практики — на курсах по математике в онлайн-школе Skysmart!
Видео:Показательная функция. 11 класс.Скачать
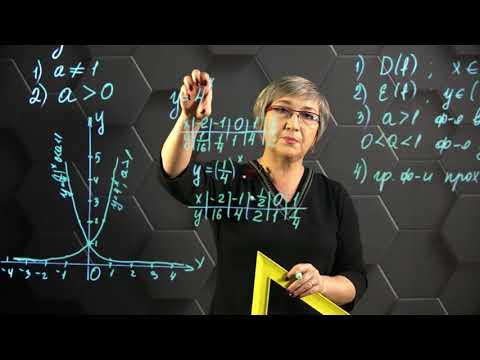
Область определения функции с корнем
Функцию с корнем можно определить так: y = n √x, где n — натуральное число больше единицы.
Рассмотрим две вариации такой функции.
Область определения корня зависит от четности или нечетности показателя:
- Если n — четное число, то есть, n = 2m, где m ∈ N, то ее область определения есть множество всех неотрицательных действительных чисел:
- Если показатель корня нечетное число больше единицы, то есть n = 2m+1, при этом m принадлежит к N, то область определения корня — множество всех действительных чисел:
Значит, область определения каждой из функций y = √x, y = 4 √x, y = 6 √x,… есть числовое множество [0, +∞). А область определения функций y = 3 √x, y = 5 √x, y = 7 √x,… — множество (−∞, +∞).
Видео:11 класс, 11 урок, Показательная функция, её свойства и графикСкачать

Пример
Найти область определения функции:
Подкоренное выражение должно быть неотрицательным, но поскольку оно стоит в знаменателе, то равняться нулю не может. Следовательно, для нахождения области определения необходимо решить неравенство x 2 + 4x + 3 > 0.
Для этого решим квадратное уравнение x 2 + 4x + 3 = 0. Находим дискриминант:
D = 16 — 12 = 4 > 0
Дискриминант положительный. Ищем корни:
Значит парабола f(x) = x 2 + 4x + 3 пересекает ось абсцисс в двух точках. Часть параболы расположена ниже оси (неравенство x 2 + 4x + 3 2 + 4x + 3 > 0).
Поскольку коэффициент a = 1 > 0, то ветви параболы смотрят вверх. Можно сделать вывод, что на интервалах (−∞, -3) ∪ (−1, +∞) выполнено неравенство x 2 + 4x + 3 > 0 (ветви параболы уходят вверх на бесконечность), а вершина параболы расположена на промежутке (-3; -1) ниже оси абсцисс, что соответствует неравенству x 2 + 4x + 3
Видео:11 класс, 12 урок, Показательные уравненияСкачать

Область определения степенной функции
Степенная функция выглядит так: y = x a , то есть, f(x) = x a , где x — переменная в основании степени, a — некоторое число в показателе степени.
Область определения степенной функции зависит от значения показателя степени.
Перечислим возможные случаи:
- Если a — положительное целое число, то область определения функции есть множество действительных чисел: (−∞, +∞).
- Для нецелых действительных положительных показателей степени: D(f) = [0, +∞).
- Если a — отрицательное целое число, то область определения функции представляет собой множество (−∞, 0) ∪ (0, +∞).
- Для остальных действительных отрицательных a область определения степенной функции — числовой промежуток (0, +∞).
При a = 0 степенная функция y = x a определена для всех действительных значений x, кроме x = 0. Это связано с тем, что мы не определяли 0 0 . А любое отличное от нуля число в нулевой степени равно единице. То есть, при a = 0 функция приобретает вид y = x 0 = 1 на области определения (−∞, 0) ∪ (0, +∞).
Рассмотрим несколько примеров.
- Область определения функций y = x 5 , y = x 12 — множество R, так как показатели степени целые положительные.
- Степенные функции
определены на интервале [0, +∞), так как их показатели положительные, но не целые.
- Область определения функции y = x −2 , как и функции y = x −5 — это множество (−∞, 0) ∪ (0, +∞), так как показатели степени целые отрицательные.
- Область определения степенных функций y = x -√19 , y = x -3e ,
— открытый числовой луч (0, +∞), так как их показатели не целые и отрицательные.
Видео:Область определения функции - 25 функций в одном видеоСкачать

Область определения показательной функции
Показательную функцию можно задать формулой y = a x , где переменная x — показатель степени, а — больше нуля и не равно единице.
Область определения показательной функции — это множество R.
Примеры показательных функций:
- y = e x
- y = (√15) x
- y = 13 x .
Область определения каждой из них (−∞, +∞).
Видео:Логарифмическая функция, ее свойства и график. 11 класс.Скачать

Область определения логарифмической функции
Логарифмическая функция выглядит так: y = logax, где где число a > 0 и a ≠ 1. Она определена на множестве всех положительных действительных чисел.
Область определения логарифмической функции или область определения логарифма — это множество всех положительных действительных чисел. То есть, D (loga) = (0, +∞).
Например:
Рассмотрим примеры логарифмических функций:
- y = log7x
- y = lnx
Область определения этих функций есть множество (0, +∞).
Видео:Это просто! Как решать Показательные Неравенства?Скачать

Пример
Укажите, какова область определения функции:
Составим и решим систему:
Ответ: область определения: D(f) = (−3, -2) ∪ (−2, +∞).
Видео:Область определения тригонометрических функцийСкачать

Область определения тригонометрических функций
Сначала вспомним, как задавать тригонометрические функции и как увидеть их области определения.
- Функция, которая задается формулой y = sinx, называется синусом, обозначается sin и определяется на множестве всех действительных чисел. Область определения синуса — это множество всех действительных чисел, то есть, D(sin) = R.
- Функция, которая задана формулой y = cosx, называется косинусом, обозначается cos и определяется на множестве R. Область определения функции косинус — множество всех действительных чисел: D(cos) = R.
- Функции, которые заданы формулами y = tgx и y = ctgx, называются тангенсом и котангенсом и обозначаются tg и ctg. Область определения тангенса — это множество всех действительных чисел, кроме чисел
. Область определения котангенса — это множество всех действительных чисел, кроме чисел πk, k ∈ Z.
Поэтому, если x — аргумент функций тангенс и котангенс, то области определения тангенса и котангенса состоят из всех таких чисел x, что 
Видео:9 класс, 15 урок, Определение числовой функции. Область определения, область значения функцииСкачать

Пример
Найдите область определения функции f(x) = tg2x.
Так как a(x) = 2x, то в область определения не войдут следующие точки:
Перенесем 2 из левой части в знаменатель правой части:
В результате 
Ответ: область определения: 
Видео:Показательная функция | 10 класс АлимовСкачать

Область определения обратных тригонометрических функций
Вспомним обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс.
- Функция, которая задается формулой y = arcsinx и рассматривается на отрезке [−1, 1], называется арксинусом и обозначается arcsin.
Область определения арксинуса — это множество [−1, 1], то есть, D(arcsin) = [−1, 1].
Функция, которая задается формулой y = arccosx и рассматривается на отрезке [−1, 1], называется арккосинусом и обозначается arccos.
Область определения функции арккосинус — отрезок [−1, 1], то есть, D(arccos) = [−1, 1].
Функции, которые задаются формулами вида y = arctgx и y = arcctgx и рассматриваются на множестве всех действительных чисел, называются арктангенсом и арккотангенсом и обозначаются arctg и arcctg.
Область определения арктангенса и арккотангенса — все множество действительных чисел R. То есть, D(arctg) = R и D(arcctg) = R.
Видео:Степенная функция. Область определенияСкачать

Таблица областей определения функций
Области определения основных функций в табличном виде можно распечатать и использовать на уроках, чтобы быстрее решать задачки.
И, помните: чем чаще вы практикуетесь в решении задач — тем быстрее все запомните.
Функция
Область определения функции
Видео:Функция. Область определения и область значений функцииСкачать
Показательные уравнения и неравенства с примерами решения
Содержание:
Рассмотрим уравнения, в которых переменная (неизвестное) находится в показателе степени. Например:
Уравнения такого вида принято называть показательными.
Видео:11 класс, 15 урок, Логарифмическая функция, её свойства и графикСкачать

Решении показательных уравнений
При решении показательных уравнений нам будет полезно следствие из теоремы о свойствах показательной функции.
Пусть
Каждому значению показательной функции 
Пример:
Решение:
Согласно следствию из равенства двух степеней с одинаковым основанием 3 следует равенство их показателей. Таким образом, данное уравнение равносильно уравнению
Пример:
Решение:
а) Данное уравнение равносильно (поясните почему) уравнению
Если степени с основанием 3 равны, то равны и их показатели:
Решив это уравнение, получим
Ответ:
При решении каждого уравнения из примера 2 сначала обе части уравнения представили в виде степени с одним и тем же основанием, а затем записали равенство показателей этих степеней.
Пример:
Решение:
а) Данное уравнение равносильно уравнению
Решая его, получаем:
Так как две степени с одинаковым основанием 2 равны, то равны и их показатели, т. е. 
б) Разделив обе части уравнения на 

Ответ:
При решении примера 3 а) левую часть уравнения разложили на множители. Причем за скобку вынесли такой множитель, что в скобках осталось числовое выражение, не содержащее переменной.
Пример:
Решить уравнение
Решение:
Обозначим 
Таким образом, из данного уравнения получаем
откуда находим:
Итак, с учетом обозначения имеем:
При решении примера 4 был использован метод введения новой переменной, который позволил свести данное уравнение к квадратному относительно этой переменной.
Пример:
Решить уравнение
Решение:
Можно заметить, что 2 — корень данного уравнения. Других корней уравнение не имеет, так как функция, стоящая в левой части уравнения, возрастающая, а функция, стоящая в правой части уравнения, убывающая. Поэтому уравнение имеет не более одного корня (см. теорему из п. 1.14).
Пример:
Решить уравнение
Решение:
Пример:
При каком значении а корнем уравнения 
Решение:
Поскольку х = 2 — корень, то верно равенство
Решив это уравнение, найдем
Ответ: при
Показательные уравнения и их системы
Показательным уравнением называется уравнение, в ко тором неизвестное входит в показатель степени. При решении показательных уравнений полезно использовать следующие тождества:
Приведем методы решения некоторых типов показательных уравнений.
1 Приведение к одному основанию.
Метод основан на следующем свойстве степеней: если две степени равны и равны их основания, то равны и их показатели, т.е. уравнения надо попытаться привести к виду 
Пример №1
Решите уравнение
Решение:
Заметим, что 
Применив тождество (1), получим Зх — 7 = -7х + 3, х = 1.
Пример №2
Решить уравнение
Решение:
Переходя к основанию степени 2, получим:
Согласно тождеству (2), имеем
Последнее уравнение равносильно уравнению 4х-19 = 2,5х.
2 Введение новой переменной.
Пример №3
Решить уравнение
Решение:
Применив тождество 2, перепишем уравнение как
Введем новую переменную: 
которое имеет корни 


Пример №4
Решить уравнение
Решение:
Разделив обе части уравнения на 
последнее уравнение запишется так:
Решая уравнение, найдем
Значение 

Пример №5
Решить уравнение
Решение:
Заметим что 
Перепишем уравнение в виде
Обозначим 
Получим
Корнями данного уравнения будут
Следовательно,
III Вынесение общего множителя за скобку.
Пример №6
Решить уравнение
Решение:
После вынесения за скобку в левой части 



Системы простейших показательных уравнений
Пример №7
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей
системе :
Очевидно, что последняя система имеет решение
Пример №8
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей системе: 
Умножив второе уравнение этой системы на (-2) и сложив с первым, получим уравнение —9х=-4. Отсюда, найдем 
Пример №9
Решите систему уравнений:
Решение:
Сделаем замену: 
Очевидно, что эта система уравнений имеет решение
Тогда получим уравнения
Приближенное решение уравнений
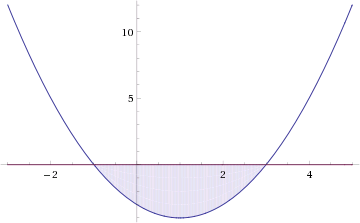
Пусть многочлен f(х) на концах отрезка [a,b] принимает значения разных знаков, то есть 

Это утверждение проиллюстрировано на следующем чертеже.
Рассмотрим отрезок 
Метод последовательного деления отрезка пополам заключается в последовательном разделении отрезка [a, b] пополам до тех пор, пока длина полученного отрезка не будет меньше заданной точности
- вычисляется значение f(х) выражения
- отрезок делится пополам, то есть вычисляется значение
- вычисляется значение
выражения f(х) в точке
- проверяется условие
- если это условие выполняется, то в качестве левого конца нового отрезка выбирается середина предыдущего отрезка, то есть полагается, что
(левый конец отрезка переходит в середину);
- если это условие не выполняется, то правый конец нового отрезка переходит в середину, то есть полагается, что b=x;
- для нового отрезка проверяется условие
- если это условие выполняется , то вычисления заканчиваются. При этом в качестве приближенного решения выбирается последнее вычисленное значение х. Если это условие не выполняется, то, переходя к пункту 2 этого алгоритма, вычисления продолжаются.
Метод последовательного деления пополам проиллюстрирован на этом чертеже:
Для нахождения интервала, содержащего корень уравнения 
Оказывается, что для корня 


Пример №10
Найдите интервал, содержащий корень уравнения
Решение:
Поделив обе части уравнения на 2 , получим,
Так как, для нового уравнения
Значит, в интервале, 




Значит, уравнение имеет корень, принадлежащий интервалу (-1; 0).
Нахождение приближенного корня с заданной точностью
Исходя из вышесказанного, заключаем, что если выполнено неравенство 



корень уравнения с точностью 




Пример №11
Найдите приближенное значение корня уравнения 
Решение:
Из предыдущего примера нам известно, что корень лежит в интервале
(-1; 0). Из того, что 
Так как, |(-0,25)41,5(-0,25)2+2,5(-0,25)+0,5| = |-0,046| 1. Если
Пусть
Изображения графиков показательной функции подсказывают это свойство. На рисунке 27 видно, что при а > 1 большему значению функции соответствует большее значение аргумента. А на рисунке 30 видно, что при 0
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Область определения (корня) функции #2. Алгебра 10 класс.Скачать

Показательные уравнения и неравенства
Решение большинства математических задач так или иначе связано с преобразованием числовых, алгебраических или функциональных выражений. Сказанное в особенности относится к решению показательных уравнений и неравенств. В вариантах ЕГЭ по математике к такому типу задач относится, в частности, задача C3. Научиться решать задания C3 важно не только с целью успешной сдачи ЕГЭ, но и по той причине, что это умение пригодится при изучении курса математики в высшей школе.
Выполняя задания C3, приходится решать различные виды уравнений и неравенств. Среди них — рациональные, иррациональные, показательные, логарифмические, тригонометрические, содержащие модули (абсолютные величины), а также комбинированные. В этой статье рассмотрены основные типы показательных уравнений и неравенств, а также различные методы их решений. О решении остальных видов уравнений и неравенств читайте в рубрике «Методическая копилка репетитора по физике и математике» в статьях, посвященных методам решения задач C3 из вариантов ЕГЭ по математике.
Прежде чем приступить к разбору конкретных показательных уравнений и неравенств, как репетитор по математике, предлагаю вам освежить в памяти некоторый теоретический материал, который нам понадобится.
Видео:Как найти область значений показательной функции.Скачать

Показательная функция
Что такое показательная функция?
Функцию вида y = a x , где a > 0 и a ≠ 1, называют показательной функцией.
Основные свойства показательной функции y = a x :
| Свойство | a > 1 | 0 только в показателях каких-либо степеней. Для решения показательных уравнений требуется знать и уметь использовать следующую несложную теорему: Помимо этого, полезно помнить об основных формулах и действиях со степенями:
Пример 1. Решите уравнение: Решение: используем приведенные выше формулы и подстановку: Уравнение тогда принимает вид: Дискриминант полученного квадратного уравнения положителен:
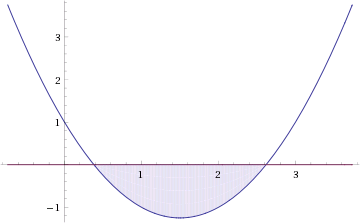
Это означает, что данное уравнение имеет два корня. Находим их: Переходя к обратной подстановке, получаем: Второе уравнение корней не имеет, поскольку показательная функция строго положительна на всей области определения. Решаем второе: С учетом сказанного в теореме 1 переходим к эквивалентному уравнению: x = 3. Это и будет являться ответом к заданию. Ответ: x = 3. Пример 2. Решите уравнение: Решение: ограничений на область допустимых значений у уравнения нет, так как подкоренное выражение имеет смысл при любом значении x (показательная функция y = 9 4 -x положительна и не равна нулю). Решаем уравнение путем равносильных преобразований с использованием правил умножения и деления степеней: Последний переход был осуществлен в соответствии с теоремой 1. Пример 3. Решите уравнение: Решение: обе части исходного уравнения можно поделить на 0,2 x . Данный переход будет являться равносильным, поскольку это выражение больше нуля при любом значении x (показательная функция строго положительна на своей области определения). Тогда уравнение принимает вид: Ответ: x = 0. Пример 4. Решите уравнение: Решение: упрощаем уравнение до элементарного путем равносильных преобразований с использованием приведенных в начале статьи правил деления и умножения степеней: Деление обеих частей уравнения на 4 x , как и в предыдущем примере, является равносильным преобразованием, поскольку данное выражение не равно нулю ни при каких значениях x. Ответ: x = 0. Пример 5. Решите уравнение: Решение: функция y = 3 x , стоящая в левой части уравнения, является возрастающей. Функция y = —x-2/3, стоящая в правой части уравнения, является убывающей. Это означает, что если графики этих функций пересекаются, то не более чем в одной точке. В данном случае нетрудно догадаться, что графики пересекаются в точке x = -1. Других корней не будет. Ответ: x = -1. Пример 6. Решите уравнение: Решение: упрощаем уравнение путем равносильных преобразований, имея в виду везде, что показательная функция строго больше нуля при любом значении x и используя правила вычисления произведения и частного степеней, приведенные в начале статьи: Ответ: x = 2. Видео:10 класс. Алгебра. Системы показательных уравнений.Скачать  Решение показательных неравенствПоказательными называются неравенства, в которых неизвестная переменная содержится только в показателях каких-либо степеней. Для решения показательных неравенств требуется знание следующей теоремы: Теорема 2. Если a > 1, то неравенство a f(x) > a g(x) равносильно неравенству того же смысла: f(x) > g(x). Если 0 f(x) > a g(x) равносильно неравенству противоположного смысла: f(x) 2x , при этом (в силу положительности функции y = 3 2x ) знак неравенства не изменится: Тогда неравенство примет вид: Итак, решением неравенства является промежуток: переходя к обратной подстановке, получаем: Левое неравенства в силу положительности показательной функции выполняется автоматически. Воспользовавшись известным свойством логарифма, переходим к эквивалентному неравенству: Поскольку в основании степени стоит число, большее единицы, эквивалентным (по теореме 2) будет переход к следующему неравенству: Итак, окончательно получаем ответ: Пример 8. Решите неравенство: Решение: используя свойства умножения и деления степеней, перепишем неравенство в виде: Введем новую переменную: С учетом этой подстановки неравенство принимает вид: Умножим числитель и знаменатель дроби на 7, получаем следующее равносильное неравенство: Итак, неравенству удовлетворяют следующие значения переменной t: Тогда, переходя к обратной подстановке, получаем: Поскольку основание степени здесь больше единицы, равносильным (по теореме 2) будет переход к неравенству: Окончательно получаем ответ: Пример 9. Решите неравенство: Решение: Делим обе части неравенства на выражение: Оно всегда больше нуля (из-за положительности показательной функции), поэтому знак неравенства изменять не нужно. Получаем: Воспользуемся заменой переменной: Исходное уравнение тогда принимает вид: Итак, неравенству удовлетворяют значения t, находящиеся в промежутке: Переходя к обратной подстановке получаем, что исходное неравенство распадается на два случая: Первое неравенство решений не имеет в силу положительности показательной функции. Решаем второе: Поскольку основание степени в данном случае оказалось меньше единицы, но больше нуля, равносильным (по теореме 2) будет переход к следующему неравенству: Итак, окончательный ответ: Пример 10. Решите неравенство: Решение: Ветви параболы y = 2x+2-x 2 направлены вниз, следовательно она ограничена сверху значением, которое она достигает в своей вершине: Ветви параболы y = x 2 -2x+2, стоящей в показателе, направлены вверх, значит она ограничена снизу значением, которое она достигает в своей вершине: Вместе с этим ограниченной снизу оказывается и функция y = 3 x 2 -2x+2 , стоящая в правой части уравнения. Она достигает своего наименьшего значения в той же точке, что и парабола, стоящая в показателе, и это значение равно 3 1 = 3. Итак, исходное неравенство может оказаться верным только в том случае, если функция слева и функция справа принимают в одной точке значение, равное 3 (пересечением областей значений этих функций является только это число). Это условие выполняется в единственной точке x = 1. Ответ: x = 1. Для того, чтобы научиться решать показательные уравнения и неравенства, необходимо постоянно тренироваться в их решении. В этом нелегком деле вам могут помочь различные методические пособия, задачники по элементарной математике, сборники конкурсных задач, занятия по математике в школе, а также индивидуальные занятия с профессиональным репетитором. Искренне желаю вам успехов в подготовке и блестящих результатов на экзамене. P. S. Уважаемые гости! Пожалуйста, не пишите в комментариях заявки на решение ваших уравнений. К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно. 💡 ВидеоАлгебра 9 класс. Область определения функцииСкачать  «Показательное уравнение» #умскул #умскул_профильнаяматематика #аделияадамоваСкачать  |

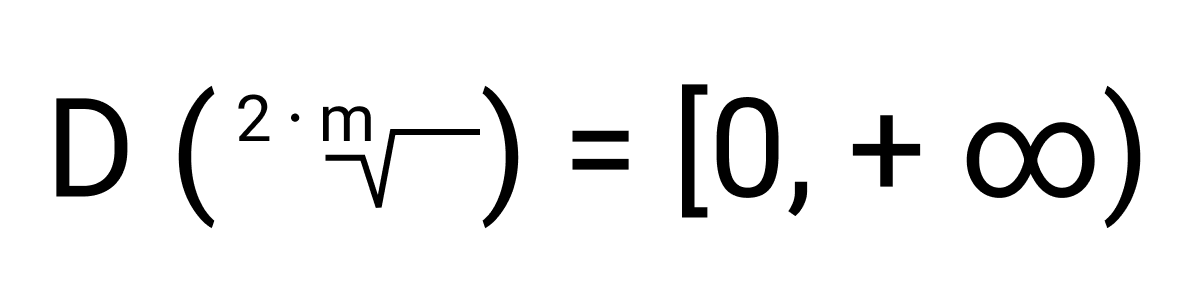
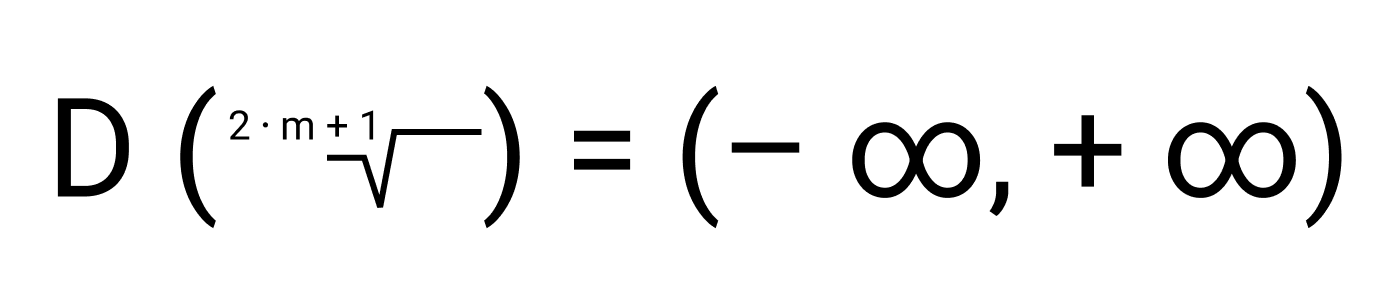


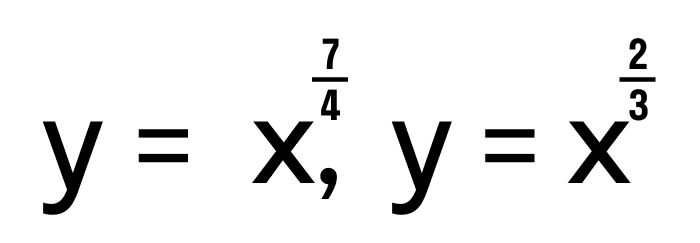 определены на интервале [0, +∞), так как их показатели положительные, но не целые.
определены на интервале [0, +∞), так как их показатели положительные, но не целые.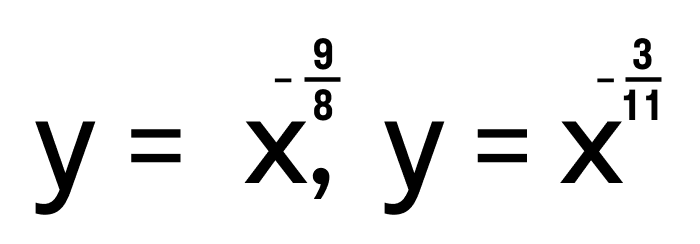 — открытый числовой луч (0, +∞), так как их показатели не целые и отрицательные.
— открытый числовой луч (0, +∞), так как их показатели не целые и отрицательные.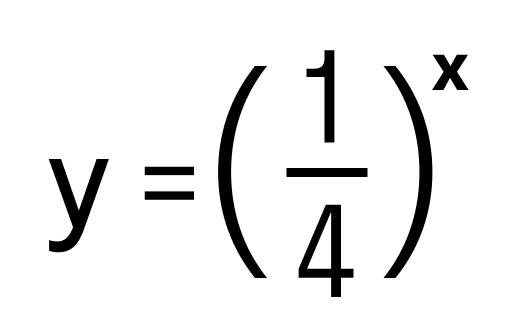
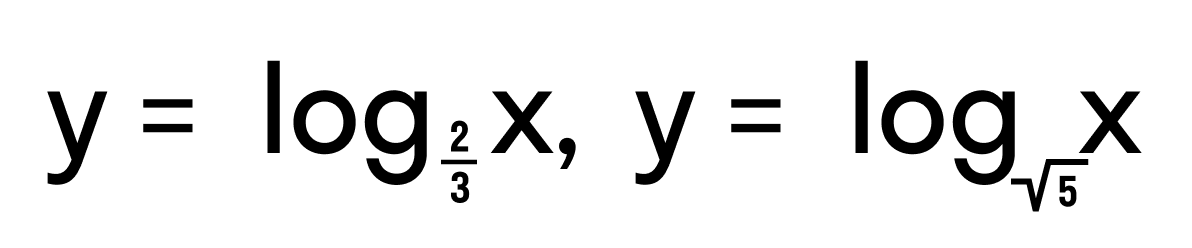



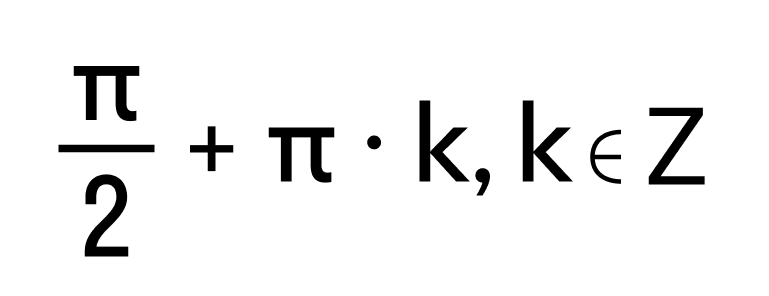 . Область определения котангенса — это множество всех действительных чисел, кроме чисел πk, k ∈ Z.
. Область определения котангенса — это множество всех действительных чисел, кроме чисел πk, k ∈ Z.












































































 выражения f(х) в точке
выражения f(х) в точке 

 (левый конец отрезка переходит в середину);
(левый конец отрезка переходит в середину);











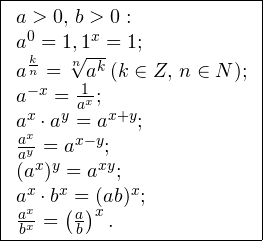 0,, b>0: \ a^0 = 1, 1^x = 1; \ a^<frac>=sqrt[n]
0,, b>0: \ a^0 = 1, 1^x = 1; \ a^<frac>=sqrt[n] 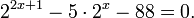
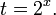
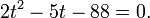
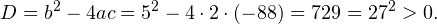 0. ]» title=»Rendered by QuickLaTeX.com»/>
0. ]» title=»Rendered by QuickLaTeX.com»/>