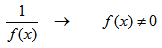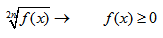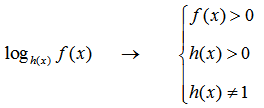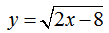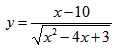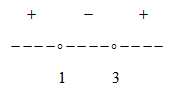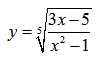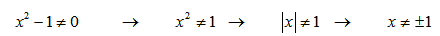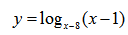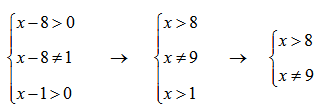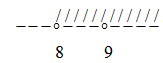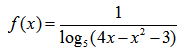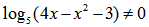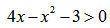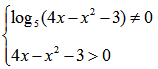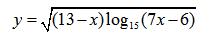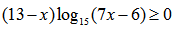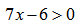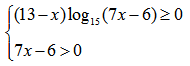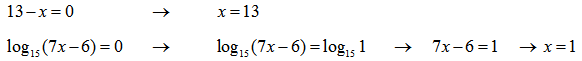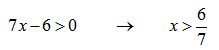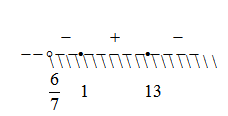О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
- Понятие области определения функции
- Материал со звездочкой
- Области определения основных элементарных функций
- Область определения постоянной функции
- Область определения функции с корнем
- Пример
- Область определения степенной функции
- Область определения показательной функции
- Область определения логарифмической функции
- Пример
- Область определения тригонометрических функций
- Пример
- Область определения обратных тригонометрических функций
- Таблица областей определения функций
- Как найти область определения функции?
- Определение:
- Областью определения называется множество значений, которые может принимать x. Обозначение D(f).
- 1. Дробная функция — ограничение на знаменатель.
- 2. Корень четной степени — ограничение на подкоренное выражение.
- 3. Логарифмы — ограничение на основание логарифма и подлогарифмическое выражение.
- 3. Тригонометрические tg(x) и ctg(x) — ограничение на аргумент.
- 4. Обратные тригонометрические функции.
- Пример нахождения области определения функции №1
- Нахождение области определения любой линейной функции, т.е. функции первой степени:
- Пример нахождения области определения функции №2
- Пример нахождения области определения функции №3
- Рассмотрим пример нахождения области определения функции с корнем четной степени:
- Пример нахождения области определения функции №4
- Рассмотрим пример нахождения области определения функции с корнем четной степени в знаменателе:
- Пример нахождения области определения функции №5
- Рассмотрим пример нахождения области определения функции с корнем нечетной степени:
- Пример нахождения области определения функции №6
- Пример нахождения области определения функции №7
- Пример нахождения области определения функции №8
- Дробно-рациональные уравнения
- Что такое дробно-рациональные уравнения
- Как решаются дробно-рациональные уравнения
- Примеры задач с ответами для 9 класса
Видео:Область ОПРЕДЕЛЕНИЯ рациональной ДРОБИ! Самое простое объяснение !Скачать

Понятие области определения функции
Впервые школьники знакомятся с термином «функция» на алгебре в 7 классе, и с каждой четвертью, с каждой новой темой это понятие раскрывается с новых сторон. И, конечно же, усложняются задачки. Сейчас дадим определения ключевым словам и будем находить область определения функции заданной формулой и по графику.
Если каждому значению x из некоторого множества соответствует число y, значит, на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у — зависимой переменной или функцией.
Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают так: y = f(x).
Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества.
Из понятия функции сформулируем определение области определения функции.
Область определения функции — это множество всех значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох. Чтобы обозначить область определения некоторой функции y, используют запись D(y).
Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.
- Например, область значений функции y = x2 — это все числа больше либо равные нулю. Это можно записать так: Е (у): у ≥ 0.
Материал со звездочкой
Старшеклассникам нужно помнить, что у некоторых функций есть собственные обозначения. Например, у тригонометрических. Поэтому в учебниках можно встретить такие записи: D(sin) — область определения функции синус, D(arcsin) — область определения функции арксинус.
Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = X. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) = [-1, 1].
Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.
Если мы хотим указать на множество чисел, которые лежат в некотором промежутке, то делаем так:
- Через точку с запятой указываем два числа: левую и правую границы промежутка.
- Если граница входит в промежуток, ставим возле нее квадратную скобку, если не входит — круглую.
- Если у промежутка нет правой границы, записываем так: ∞ или +∞. Если нет левой границы, пишем -∞.
- Если нужно описать множество, состоящее из нескольких промежутков, ставим между ними знак объединения: ∪.
Например, все действительные числа от 2 до 5 включительно можно записать так:
Все положительные числа можно описать так:
Ноль не положительное число, поэтому скобка возле него круглая.
Видео:Функция. Область определения функции. Практическая часть. 10 класс.Скачать

Области определения основных элементарных функций
Область определения функции — неотъемлемая часть самой функции. Когда мы вводим какую-либо функцию, то сразу указываем ее область определения.
На уроках алгебры мы последовательно знакомимся с каждой функцией: прямая пропорциональность, линейная функция, функция y = x2 и другие. А области их определения изучаем, как свойства.
Рассмотрим области определения основных элементарных функций.
Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Область определения постоянной функции
Постоянная функция задается формулой y = C, то есть f(x) = C, где C — некоторое действительное число. Ее еще называют константа.
Смысл функции — в том, что каждому значению аргумента соответствует значение функции, которое равно C. Поэтому, область определения этой функции — множество всех действительных чисел R.
- Область определения постоянной функции y = -3 — это множество всех действительных чисел: D(y) = (−∞, +∞) или D(y) = R.
- Областью определения функции y = 3 √9 является множество R.
Еще больше наглядных примеров и практики — на курсах по математике в онлайн-школе Skysmart!
Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Область определения функции с корнем
Функцию с корнем можно определить так: y = n √x, где n — натуральное число больше единицы.
Рассмотрим две вариации такой функции.
Область определения корня зависит от четности или нечетности показателя:
- Если n — четное число, то есть, n = 2m, где m ∈ N, то ее область определения есть множество всех неотрицательных действительных чисел:
- Если показатель корня нечетное число больше единицы, то есть n = 2m+1, при этом m принадлежит к N, то область определения корня — множество всех действительных чисел:
Значит, область определения каждой из функций y = √x, y = 4 √x, y = 6 √x,… есть числовое множество [0, +∞). А область определения функций y = 3 √x, y = 5 √x, y = 7 √x,… — множество (−∞, +∞).
Видео:Как найти область определения функции? #shortsСкачать

Пример
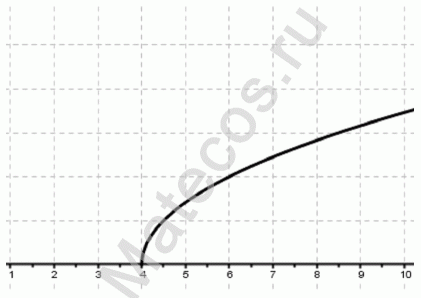
Найти область определения функции:
Подкоренное выражение должно быть неотрицательным, но поскольку оно стоит в знаменателе, то равняться нулю не может. Следовательно, для нахождения области определения необходимо решить неравенство x 2 + 4x + 3 > 0.
Для этого решим квадратное уравнение x 2 + 4x + 3 = 0. Находим дискриминант:
D = 16 — 12 = 4 > 0
Дискриминант положительный. Ищем корни:
Значит парабола f(x) = x 2 + 4x + 3 пересекает ось абсцисс в двух точках. Часть параболы расположена ниже оси (неравенство x 2 + 4x + 3 2 + 4x + 3 > 0).
Поскольку коэффициент a = 1 > 0, то ветви параболы смотрят вверх. Можно сделать вывод, что на интервалах (−∞, -3) ∪ (−1, +∞) выполнено неравенство x 2 + 4x + 3 > 0 (ветви параболы уходят вверх на бесконечность), а вершина параболы расположена на промежутке (-3; -1) ниже оси абсцисс, что соответствует неравенству x 2 + 4x + 3
Видео:Область определения функции - 25 функций в одном видеоСкачать

Область определения степенной функции
Степенная функция выглядит так: y = x a , то есть, f(x) = x a , где x — переменная в основании степени, a — некоторое число в показателе степени.
Область определения степенной функции зависит от значения показателя степени.
Перечислим возможные случаи:
- Если a — положительное целое число, то область определения функции есть множество действительных чисел: (−∞, +∞).
- Для нецелых действительных положительных показателей степени: D(f) = [0, +∞).
- Если a — отрицательное целое число, то область определения функции представляет собой множество (−∞, 0) ∪ (0, +∞).
- Для остальных действительных отрицательных a область определения степенной функции — числовой промежуток (0, +∞).
При a = 0 степенная функция y = x a определена для всех действительных значений x, кроме x = 0. Это связано с тем, что мы не определяли 0 0 . А любое отличное от нуля число в нулевой степени равно единице. То есть, при a = 0 функция приобретает вид y = x 0 = 1 на области определения (−∞, 0) ∪ (0, +∞).
Рассмотрим несколько примеров.
- Область определения функций y = x 5 , y = x 12 — множество R, так как показатели степени целые положительные.
- Степенные функции
определены на интервале [0, +∞), так как их показатели положительные, но не целые.
- Область определения функции y = x −2 , как и функции y = x −5 — это множество (−∞, 0) ∪ (0, +∞), так как показатели степени целые отрицательные.
- Область определения степенных функций y = x -√19 , y = x -3e ,
— открытый числовой луч (0, +∞), так как их показатели не целые и отрицательные.
Видео:Алгебра 9 класс. Область определения функцииСкачать

Область определения показательной функции
Показательную функцию можно задать формулой y = a x , где переменная x — показатель степени, а — больше нуля и не равно единице.
Область определения показательной функции — это множество R.
Примеры показательных функций:
- y = e x
- y = (√15) x
- y = 13 x .
Область определения каждой из них (−∞, +∞).
Видео:9 класс, 15 урок, Определение числовой функции. Область определения, область значения функцииСкачать

Область определения логарифмической функции
Логарифмическая функция выглядит так: y = logax, где где число a > 0 и a ≠ 1. Она определена на множестве всех положительных действительных чисел.
Область определения логарифмической функции или область определения логарифма — это множество всех положительных действительных чисел. То есть, D (loga) = (0, +∞).
Например:
Рассмотрим примеры логарифмических функций:
- y = log7x
- y = lnx
Область определения этих функций есть множество (0, +∞).
Видео:Дробно рациональные уравнения. Алгебра, 9 классСкачать

Пример
Укажите, какова область определения функции:
Составим и решим систему:
Ответ: область определения: D(f) = (−3, -2) ∪ (−2, +∞).
Видео:Алгебра 8. Урок 11 - Дробно-рациональные уравненияСкачать

Область определения тригонометрических функций
Сначала вспомним, как задавать тригонометрические функции и как увидеть их области определения.
- Функция, которая задается формулой y = sinx, называется синусом, обозначается sin и определяется на множестве всех действительных чисел. Область определения синуса — это множество всех действительных чисел, то есть, D(sin) = R.
- Функция, которая задана формулой y = cosx, называется косинусом, обозначается cos и определяется на множестве R. Область определения функции косинус — множество всех действительных чисел: D(cos) = R.
- Функции, которые заданы формулами y = tgx и y = ctgx, называются тангенсом и котангенсом и обозначаются tg и ctg. Область определения тангенса — это множество всех действительных чисел, кроме чисел
. Область определения котангенса — это множество всех действительных чисел, кроме чисел πk, k ∈ Z.
Поэтому, если x — аргумент функций тангенс и котангенс, то области определения тангенса и котангенса состоят из всех таких чисел x, что 
Видео:Область определения функцийСкачать

Пример
Найдите область определения функции f(x) = tg2x.
Так как a(x) = 2x, то в область определения не войдут следующие точки:
Перенесем 2 из левой части в знаменатель правой части:
В результате 
Ответ: область определения: 
Видео:§39.1 Нахождение области определения алгебраического выраженияСкачать

Область определения обратных тригонометрических функций
Вспомним обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс.
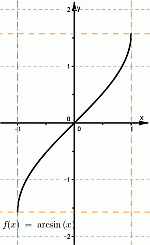
- Функция, которая задается формулой y = arcsinx и рассматривается на отрезке [−1, 1], называется арксинусом и обозначается arcsin.
Область определения арксинуса — это множество [−1, 1], то есть, D(arcsin) = [−1, 1].
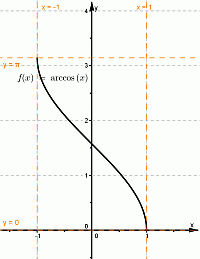
Функция, которая задается формулой y = arccosx и рассматривается на отрезке [−1, 1], называется арккосинусом и обозначается arccos.
Область определения функции арккосинус — отрезок [−1, 1], то есть, D(arccos) = [−1, 1].
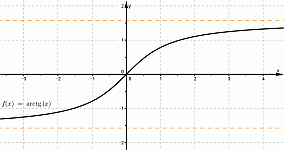
Функции, которые задаются формулами вида y = arctgx и y = arcctgx и рассматриваются на множестве всех действительных чисел, называются арктангенсом и арккотангенсом и обозначаются arctg и arcctg.
Область определения арктангенса и арккотангенса — все множество действительных чисел R. То есть, D(arctg) = R и D(arcctg) = R.
Видео:Область определения (дроби) функции #1. Алгебра 10 класс.Скачать

Таблица областей определения функций
Области определения основных функций в табличном виде можно распечатать и использовать на уроках, чтобы быстрее решать задачки.
И, помните: чем чаще вы практикуетесь в решении задач — тем быстрее все запомните.
Функция
Область определения функции
Видео:Область определения (корня) функции #2. Алгебра 10 класс.Скачать

Как найти область определения функции?
 |
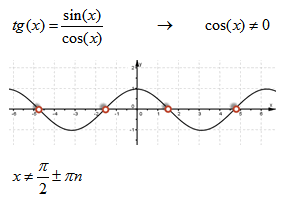 | на графике тангенса | 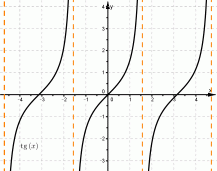 |
Для котангенса:
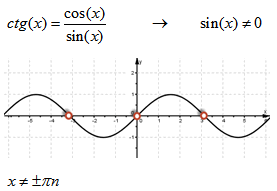 | на графике котангенса | 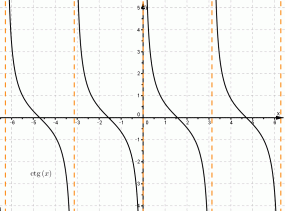 |
4. Обратные тригонометрические функции.
| Арксинус | Арккосинус | Арктангенс, Арккотангенс |
 |  |  |
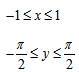
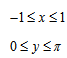
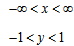
| Пример 1 | Пример 2 |
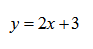 | 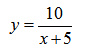 |
| Пример 3 | Пример 4 |
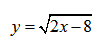 | 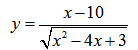 |
| Пример 5 | Пример 6 |
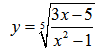 | 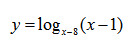 |
| Пример 7 | Пример 8 |
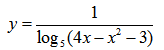 | 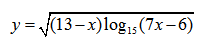 |
| Пример 9 | Пример 10 |
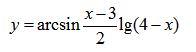 | 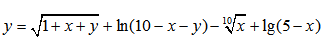 |
| Пример 11 | Пример 12 |
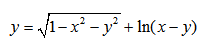 | 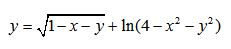 |
| Пример 13 | Пример 14 |
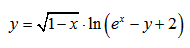 |
| Пример 15 | Пример 16 |
Пример нахождения области определения функции №1
Видео:Алгебра 8. Урок 1 - Рациональное выражение и его ОДЗСкачать

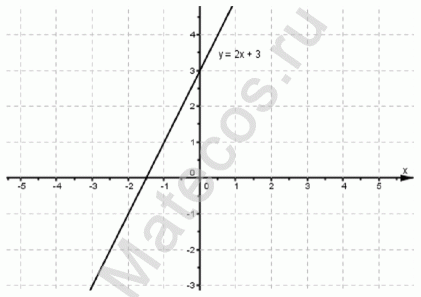
Нахождение области определения любой линейной функции, т.е. функции первой степени:
y = 2x + 3 — уравнение задает прямую на плоскости.
Посмотрим внимательно на функцию и подумаем, какие же числовые значения мы сможем подставить в уравнение вместо переменной х?
Попробуем подставить значение х=0
Так как y = 2·0 + 3 = 3 — получили числовое значение, следовательно функция существует при взятом значении переменной х=0.
Попробуем подставить значение х=10
так как y = 2·10 + 3 = 23 — функция существует при взятом значении переменной х=10 .
Попробуем подставить значение х=-10
так как y = 2·(-10) + 3 = -17 — функция существует при взятом значении переменной х=-10 .
Уравнение задает прямую линию на плоcкости, а прямая не имеет ни начала ни конца, следовательно она существует для любых значений х.
Заметим, что какие бы числовые значения мы не подставляли в заданную функцию вместо х, всегда получим числовое значение переменной y.
Следовательно, функция существует для любого значения x ∈ R или запишем так: D(f) = R
Формы записи ответа: D(f)=R или D(f)=(-∞:+∞)или x∈R или x∈(-∞:+∞)
Для любой функции вида y = ax + b областью определения является множество действительных чисел.
Пример нахождения области определения функции №2
Задана функция вида:
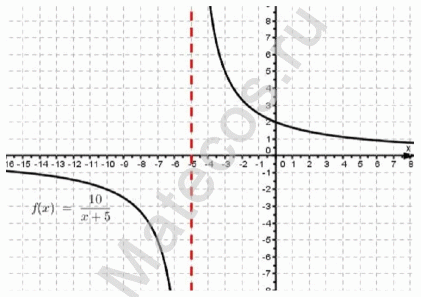
y = 10/(x + 5) — уравнение гиперболы
Имея дело с дробной функцией, вспомним, что на ноль делить нельзя. Следовательно функция будет существовать для всех значений х, которые не
обращают знаменатель в ноль. Попробуем подставить какие-либо произвольные значения х.
При х = 0 имеем y = 10/(0 + 5) = 2 — функция существует.
При х = 10 имеем y = 10/(10 + 5) = 10/15 = 2/ 3 — функция существует.
При х = -5 имеем y = 10/(-5 + 5) = 10/0 — функция в этой точке не существует.
Т.е. если заданная функция дробная, то необходимо знаменатель приравнять нулю и найти такую точку, в которой функция не существует.
x + 5 = 0 → x = -5 — в этой точке заданная функция не существует.
Для наглядности изобразим графически:
На графике также видим, что гипербола максимально близко приближается к прямой х = -5 , но самого значения -5 не достигает.
Видим, что заданная функция существует во всех точках действительной оси, кроме точки x = -5
Формы записи ответа: D(f)=R или D(f)=(-∞;-5) ∪ (-5;+∞) или x ∈ R или x ∈ (-∞;-5) ∪ (-5;+∞)
Если заданная функция дробная, то наличие знаменателя накладывает условие неравенства нулю знаменателя.
Пример нахождения области определения функции №3
Видео:Функция. Область определения и область значений функцииСкачать
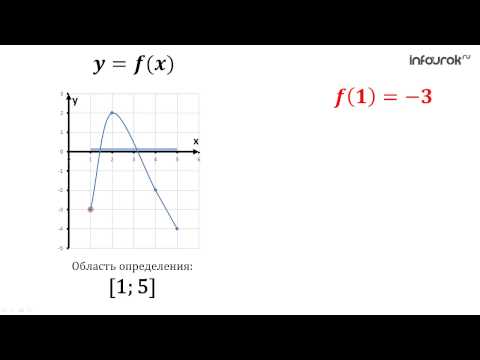
Рассмотрим пример нахождения области определения функции с корнем четной степени:
Так как квадратный корень мы можем извлечь только из неотрицательного числа, следовательно, функция под корнем — неотрицательна.
Решим простое неравенство:
2х — 8 ≥ 0 → 2х ≥ 8 → х ≥ 4
Заданная функция существует только при найденных значениях х ≥ 4 или D(f)=[4 ;+∞) или x ∈ [4 ;+∞) .
На графике видим, что функция существует для найденных значений х : х ≥ 4 или D(f)=[4 ;+∞) или x ∈ [4 ;+∞) .
При попытке подставить вместо х значения, отличные от найденных, под корнем получим отрицательное число, те в этих точках функция не существует.
Если заданная функция содержит квадратный корень (или корень любой четной степени), то обязательно накладывается условие неотрицательности (≥0) на подкоренное выражение. Если квадратный корень находится в знаменателе функции, у которой мы находим область определения, то на подкоренное выражение накладывается условие положительности (>0), так как знаменатель всегда должен быть отличен от нуля.
Пример нахождения области определения функции №4
Видео:Область определения дробных выраженийСкачать

Рассмотрим пример нахождения области определения функции с корнем четной степени в знаменателе:
В числителе имеем линейную функцию, область определения которой множество всех действительных чисел. (см. пример 1)
В знаменателе — квадратный корень, накладывает условие на подкоренное выражение, не забывая о том, что знаменатель всегда отличен от нуля.
x 2 — 4x + 3 > 0 → (x — 1)(x — 3) > 0
Решим строгое неравенство методом интервалов:
Видим, что функция положительна на следующих интервалах: x∈(-∞;1)∪(3;+∞)
Нашли такие значения переменной х, при которых функция существует — нашли ОДЗ функции.
Пример нахождения области определения функции №5
Видео:СПОРИМ ты поймешь Математику — Функция и ее свойства, Область определения, Нули ФункцииСкачать

Рассмотрим пример нахождения области определения функции с корнем нечетной степени:
Имеем дело с корнем нечетной степени. Так как корень нечетной степени существует при любых значениях подкоренного выражения, то заданная дробная функция под корнем может принимать любые значения.
В числителе дробной функции — уравнение первой сnепени, которое существует при любых значениях переменной. Знаменатель любой дроби отличен от нуля. Следовательно, при нахождении ОДЗ заданного выражения имеем дело лишь с одним ограничением — ограничение на знаменатель дроби.
Пример нахождения области определения функции №6
Рассмотрим пример нахождения области определения логарифма:
Простенький пример на область определения логарифмической функции.
Помним, что основание логарифма положительно и отлично от нуля. Подлогарифмическое выражение положительно:
Покажем на числовой прямой:
Получили ОДЗ: x∈(8;9)∪(9;+∞)
Пример нахождения области определения функции №7
Задана функция вида:
1 ограничение основывается на наложении ограничения на знаменатель дроби (отличен от нуля):
Второе ограничение — подлогарифмическое выражение положительно:
Т.е. для определения области определения заданной функции необходимо решить систему:
Необходимо решить каждое из ограничений системы по отдельности и пересечь получившиеся результаты.
Допускаю, что читатель самостоятельно может это проделать и перехожу к разбору следующего примера.
Пример нахождения области определения функции №8
Рассмотрим следующий пример:
Имеем дело с корнем четной степени, следовательно первое ограничение на подкоренное выражение:
Имеем дело с логарифмом, следовательно ограничение на подлогарифмическую функцию:
Таким образом для определения области определения исходной функции необходимо решить систему неравенств:
Каждое из неравенств решим по отдельности.
Первое неравенство будем решать методом интервалов: найдем корни каждого из выражений неравенства, вынесем их на координатную плоскость и расставим знаки неравенства в каждом из полученных интервалов.
Выносим на координатную прямую:
Объясню как расставлены знаки в каждом из интервалов:
Значения левее 6/7 нет смысла рассматривать, так как логарифм для этих значений не существует.
1-ый интервал: (6/7;1]
Основание логарифма больше единицы, следовательно функция возрастающая. В корне x=1 логарифм меняет свое значение с » — » на » + «.
Дробно-рациональные уравнения
Что такое дробно-рациональные уравнения
Дробно-рациональными уравнениями называют такие выражения, которые представляется возможным записать, как:
при P ( x ) и Q ( x ) в виде выражений, содержащих переменную.
Таким образом, дробно-рациональные уравнения обязательно содержат как минимум одну дробь с переменной в знаменателе с любым модулем.
9 x 2 — 1 3 x = 0
1 2 x + x x + 1 = 1 2
6 x + 1 = x 2 — 5 x x + 1
Уравнения, которые не являются дробно-рациональными:
Как решаются дробно-рациональные уравнения
В процессе решения дробно-рациональных уравнений обязательным действием является определение области допустимых значений. Найденные корни следует проверить на допустимость, чтобы исключить посторонние решения.
Алгоритм действий при стандартном способе решения:
- Выписать и определить ОДЗ.
- Найти общий знаменатель для дробей.
- Умножить каждый из членов выражения на полученный общий параметр (знаменатель), сократить дроби, которые получились в результате, чтобы исключить знаменатели.
- Записать уравнение со скобками.
- Раскрыть скобки для приведения подобных слагаемых.
- Найти корни полученного уравнения.
- Выполним проверку корней в соответствии с ОДЗ.
- Записать ответ.
Пример 1
Разберем предложенный алгоритм на практическом примере. Предположим, что имеется дробно-рациональное уравнение, которое требуется решить:
x x — 2 — 7 x + 2 = 8 x 2 — 4
Начать следует с области допустимых значений:
x 2 — 4 ≠ 0 ⇔ x ≠ ± 2
Воспользуемся правилом сокращенного умножения:
x 2 — 4 = ( x — 2 ) ( x + 2 )
В результате общим знаменателем дробей является:
Выполним умножение каждого из членов выражения на общий знаменатель:
x x — 2 — 7 x + 2 = 8 x 2 — 4
x ( x — 2 ) ( x + 2 ) x — 2 — 7 ( x — 2 ) ( x + 2 ) x + 2 = 8 ( x — 2 ) ( x + 2 ) ( x — 2 ) ( x + 2 )
После сокращения избавимся от скобок и приведем подобные слагаемые:
x ( x + 2 ) — 7 ( x — 2 ) = 8
x 2 + 2 x — 7 x + 14 = 8
Осталось решить квадратное уравнение:
Согласно ОДЗ, первый корень является лишним, так как не удовлетворяет условию, по которому корень не равен 2. Тогда в ответе можно записать:
Примеры задач с ответами для 9 класса
Требуется решить дробно-рациональное уравнение:
x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0
x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0
Определим область допустимых значений:
О Д З : x + 2 ≠ 0 ⇔ x ≠ — 2
x 2 + 7 x + 10 ≠ 0
D = 49 — 4 · 10 = 9
x 1 ≠ — 7 + 3 2 = — 2
x 2 ≠ — 7 — 3 2 = — 5
Квадратный трехчлен x 2 + 7 x + 10 следует разложить на множители, руководствуясь формулой:
a x 2 + b x + c = a ( x — x 1 ) ( x — x 2 )
x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0
Заметим, что общим знаменателем для дробей является: ( x + 2 ) ( x + 5 ) . Умножим на этот знаменатель уравнение:
x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0
Сократим дроби, избавимся от скобок, приведем подобные слагаемые:
x ( x + 2 ) ( x + 5 ) x + 2 + ( x + 1 ) ( x + 2 ) ( x + 5 ) x + 5 —
— ( 7 — x ) ( x + 2 ) ( x + 5 ) ( x + 2 ) ( x + 5 ) = 0
x ( x + 5 ) + ( x + 1 ) ( x + 2 ) — 7 + x = 0
x 2 + 5 x + x 2 + 3 x + 2 — 7 + x = 0
2 x 2 + 9 x — 5 = 0
Потребуется решить квадратное уравнение:
2 x 2 + 9 x — 5 = 0
Первый корень не удовлетворяет условиям ОДЗ, поэтому в ответ нужно записать только второй корень.
Дано дробно-рациональное уравнение, корни которого требуется найти:
4 x — 2 — 3 x + 4 = 1
В первую очередь следует переместить все слагаемые влево и привести дроби к минимальному единому знаменателю:
4 ( x + 4 ) x — 2 — 3 ( x — 2 ) x + 4 — 1 ( x — 2 ) ( x + 4 ) = 0
4 ( x + 4 ) — 3 ( x — 2 ) — ( x — 2 ) ( x + 4 ) ( x — 2 ) ( x + 4 ) = 0
4 x + 16 — 3 x + 6 — ( x 2 + 4 x — 2 x — 8 ) ( x — 2 ) ( x + 4 ) = 0
x + 22 — x 2 — 4 x + 2 x + 8 ( x — 2 ) ( x + 4 ) = 0
Заметим, что получилось нулевое значение для дроби. Известно, что дробь может равняться нулю, если в числителе нуль, а знаменатель не равен нулю. На основании этого можно составить систему:
— x 2 — x + 30 ( x — 2 ) ( x + 4 ) = 0 ⇔ — x 2 — x + 30 = 0 ( x — 2 ) ( x + 4 ) ≠ 0
Следует определить такие значения для переменной, при которых в дроби знаменатель будет обращаться в нуль. Такие значения необходимо удалить из ОДЗ:
( x — 2 ) ( x + 4 ) ≠ 0
Далее можно определить значения для переменных, которые при подстановке в уравнение обращают числитель в нуль:
— x 2 — x + 30 = 0 _ _ _ · ( — 1 )
Получилось квадратное уравнение, которое можно решить:
Сравнив корни с условиями области допустимых значений, можно сделать вывод, что оба корня являются решениями данного уравнения.
Нужно решить дробно-рациональное уравнение:
x + 2 x 2 — 2 x — x x — 2 = 3 x
На первом шаге следует перенести все слагаемые в одну сторону и привести дроби к минимальному единому знаменателю:
x + 2 1 x ( x — 2 ) — x x x — 2 — 3 ( x — 2 ) x = 0
x + 2 — x 2 — 3 ( x — 2 ) x ( x — 2 ) = 0
x + 2 — x 2 — 3 x + 6 x ( x — 2 ) = 0
— x 2 — 2 x + 8 x ( x — 2 ) = 0 ⇔ — x 2 — 2 x + 8 = 0 x ( x — 2 ) ≠ 0
Перечисленные значения переменной обращают знаменатель в нуль. По этой причине их необходимо удалить из области допустимых значений.
— x 2 — 2 x + 8 = 0 _ _ _ · ( — 1 )
Корни квадратного уравнения:
x 1 = — 4 ; x 2 = 2
Заметим, что второй корень не соответствует ОДЗ. Таким образом, в ответе остается только первый корень.
Найти корни уравнения:
x 2 — x — 6 x — 3 = x + 2
Согласно стандартному алгоритму решения дробно-рациональных уравнений, выполним перенос всех слагаемых в одну сторону. Далее необходимо привести к дроби к наименьшему общему знаменателю:
x 2 — x — 6 1 x — 3 — x ( x — 3 ) — 2 ( x — 3 ) = 0
x 2 — x — 6 — x ( x — 3 ) — 2 ( x — 3 ) x — 3 = 0
x 2 — x — 6 — x 2 + 3 x — 2 x + 6 x — 3 = 0
0 x x — 3 = 0 ⇔ 0 x = 0 x — 3 ≠ 0
Такое значение переменной, при котором знаменатель становится равным нулю, нужно исключить из области допустимых значений:
Заметим, что это частный случай линейного уравнения, которое обладает бесконечным множеством корней. При подстановке какого-либо числа на место переменной х в любом случае числовое равенство будет справедливым. Единственным недопустимым значением для х в данном задании является число 3, которое не входит в ОДЗ.
Ответ: х — любое число, за исключением 3.
Требуется вычислить корни дробно-рационального уравнения:
5 x — 2 — 3 x + 2 = 20 x 2 — 4
На первом этапе необходимо выполнить перенос всех слагаемых влево, привести дроби к минимальному единому знаменателю:
5 ( x + 2 ) x — 2 — 3 ( x — 2 ) x + 2 — 20 1 ( x — 2 ) ( x + 2 ) = 0
5 ( x + 2 ) — 3 ( x — 2 ) — 20 ( x — 2 ) ( x + 2 ) = 0
5 x + 10 — 3 x + 6 — 20 ( x — 2 ) ( x + 2 ) = 0
2 x — 4 ( x — 2 ) ( x + 2 ) = 0 ⇔ 2 x — 4 = 0 ( x — 2 ) ( x + 2 ) ≠ 0
( x — 2 ) ( x + 2 ) ≠ 0
Данные значения переменной х являются недопустимыми, так как в этом случае теряется смысл дроби в связи с тем, что знаменатель принимает нулевое значение.
Заметим, что 2 не входит в область допустимых значений. В связи с этим, можно заключить, что у уравнения отсутствуют корни.
Ответ: корни отсутствуют
Нужно найти корни уравнения:
x — 3 x — 5 + 1 x = x + 5 x ( x — 5 )
Начнем с определения ОДЗ:
— 5 ≠ 0 x ≠ 0 x ( x — 5 ) ≠ 0 x ≠ 5 x ≠ 0
При умножении обеих частей уравнения на единый знаменатель всех дробей и сокращении аналогичных выражений, которые записаны в числителе и знаменателе, получим:
x — 3 x — 5 + 1 x = x + 5 x ( x — 5 ) · x ( x — 5 )
( x — 3 ) x ( x — 5 ) x — 5 + x ( x — 5 ) x = ( x + 5 ) x ( x — 5 ) x ( x — 5 )
( x — 3 ) x + x = x + 5
Прибегая к арифметическим преобразованиям, можно записать уравнение в упрощенной форме:
x 2 — 3 x + x — 5 = x + 5 → x 2 — 2 x — 5 — x — 5 = 0 → x 2 — 3 x — 10 = 0
Для дальнейших действий следует определить, к какому виду относится полученное уравнение. В нашем случае уравнение является квадратным с коэффициентом при x 2 , который равен 1. Таким образом, целесообразно воспользоваться теоремой Виета:
x 1 · x 2 = — 10 x 1 + x 2 = 3
В этом случае подходящими являются числа: -2 и 5.
Второе значение не соответствует области допустимых значений.

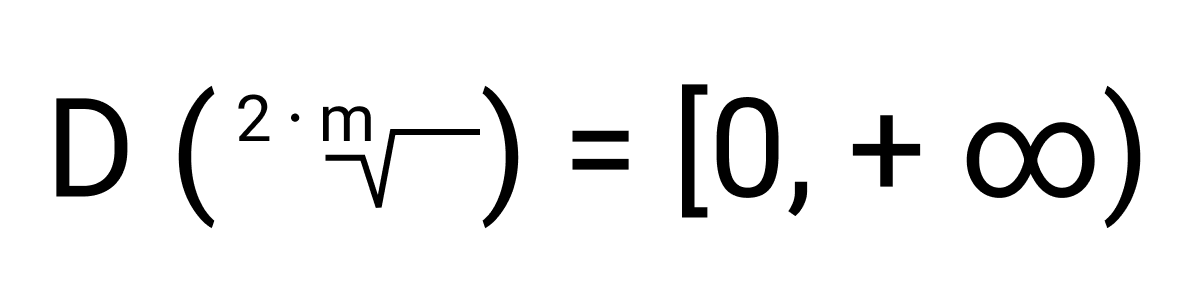
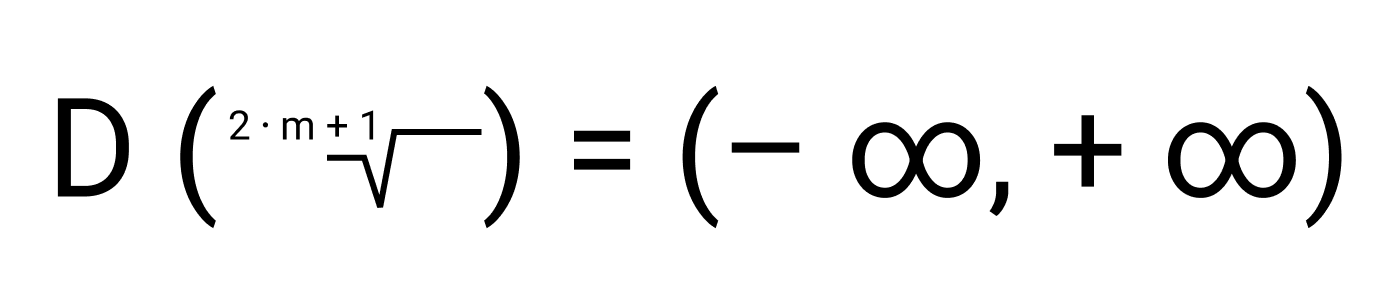


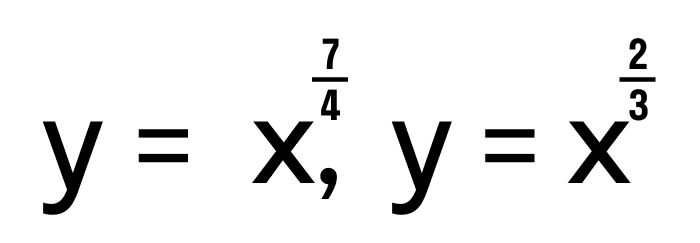 определены на интервале [0, +∞), так как их показатели положительные, но не целые.
определены на интервале [0, +∞), так как их показатели положительные, но не целые.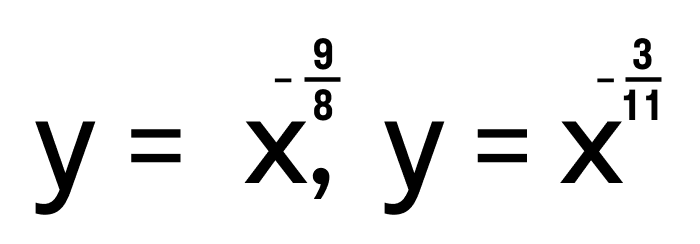 — открытый числовой луч (0, +∞), так как их показатели не целые и отрицательные.
— открытый числовой луч (0, +∞), так как их показатели не целые и отрицательные.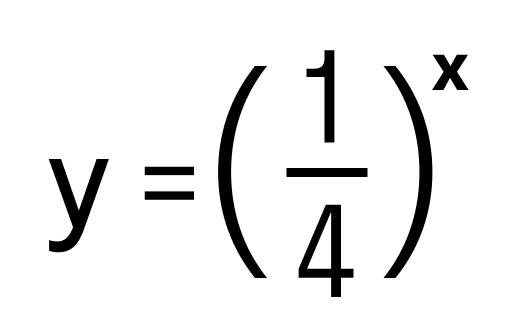
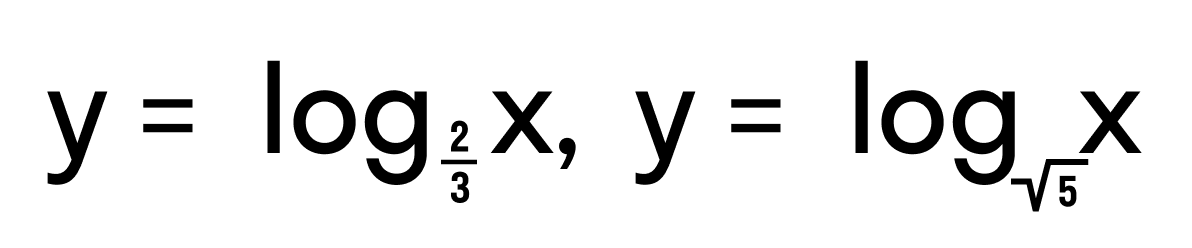



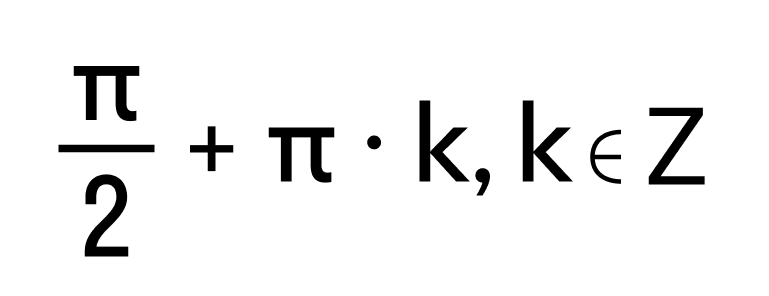 . Область определения котангенса — это множество всех действительных чисел, кроме чисел πk, k ∈ Z.
. Область определения котангенса — это множество всех действительных чисел, кроме чисел πk, k ∈ Z.