О чем эта статья:
- Понятие функции
- Понятие линейной функции
- Свойства линейной функции
- Построение линейной функции
- Решение задач на линейную функцию
- Тест по математике «Линейные уравнения с двумя переменными» (7 класс)
- Математика: теория и методика преподавания в образовательной организации
- Дистанционное обучение как современный формат преподавания
- Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Урок по теме «Уравнение касательной к графику» для 10-х классов с углубленным изучением математики
- Ход урока
- 1. Устная работа
- 2. Проверка домашней работы.
- 3. Работа в группах.
- 4. Итог урока.
- 📽️ Видео
Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Понятие функции
| Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции. |
|---|
Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:
Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.
Графический способ — наглядно. Его мы и разберем в этой статье.
| График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу. |
|---|
Видео:Уравнение прямой по графику. ПримерыСкачать

Понятие линейной функции
| Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент. |
|---|
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Нам дана функция: у = 0,5х — 2. Значит:
если х = 0, то у = -2;
если х = 2, то у = -1;
если х = 4, то у = 0 и т. д.
Для удобства результаты можно оформлять в виде таблицы:
| х | 0 | 2 | 4 |
| y | -2 | -1 | 0 |
Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.
| Функция | Коэффициент k | Коэффициент b |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.
Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Свойства линейной функции
Область определения функции — множество всех действительных чисел.
Множеством значений функции является множество всех действительных чисел.
График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.
Функция не имеет ни наибольшего, ни наименьшего значений.
Четность и нечетность линейной функции зависят от значений коэффициентов k и b:
b ≠ 0, k = 0, значит, y = b — четная;
b = 0, k ≠ 0, значит, y = kx — нечетная;
b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;
b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.
Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.
График функции пересекает оси координат:
ось абсцисс ОХ — в точке (−b/k; 0);
ось ординат OY — в точке (0; b).
x = −b/k — является нулем функции.
Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.
Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.
Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).
При k 0, то этот угол острый, если k
Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
если k > 0, то график наклонен вправо;
если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
если b 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Если k > 0 и b
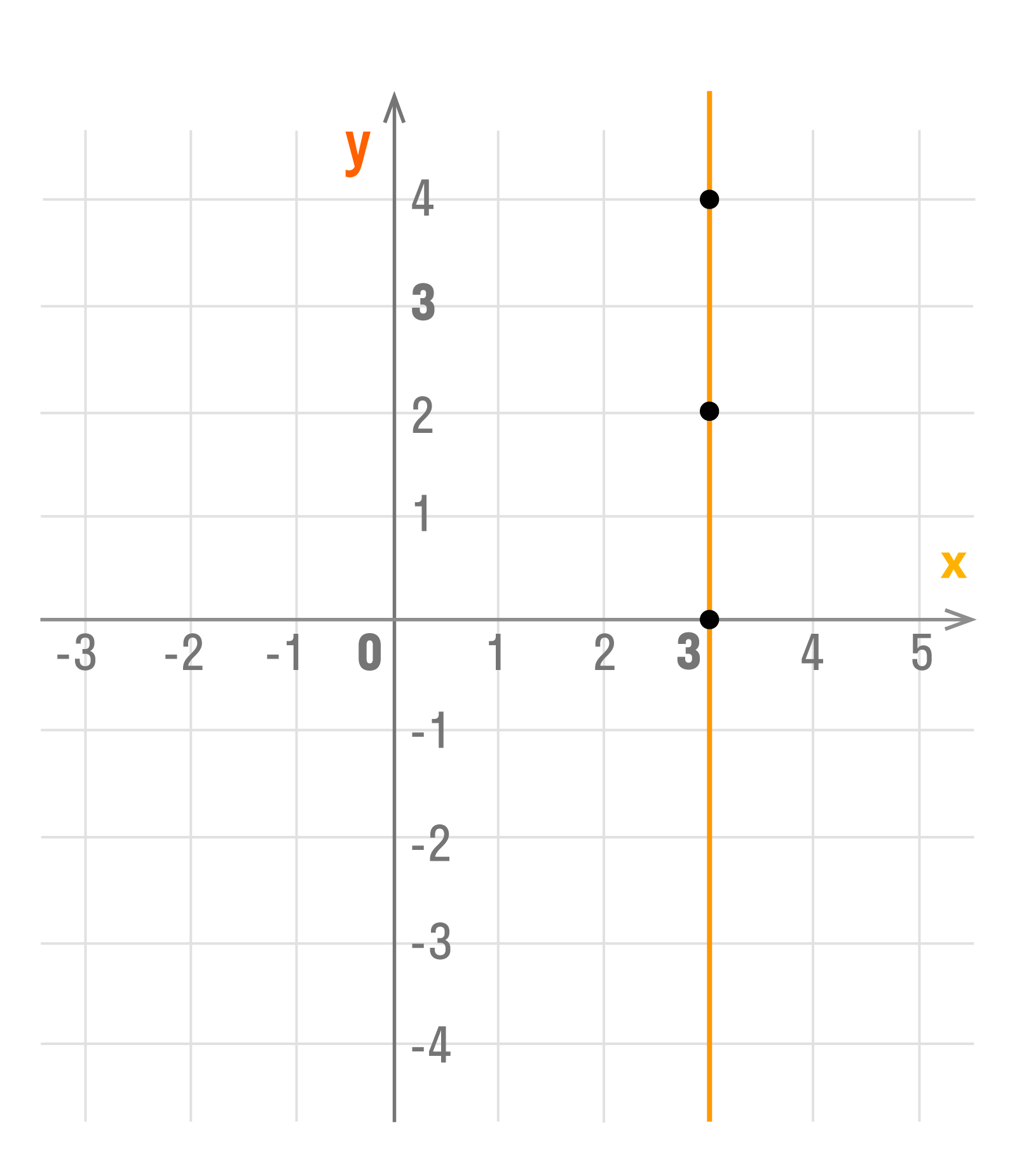
В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.
Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.
Например, график уравнения х = 3:
Условие параллельности двух прямых:
График функции y = k1x + b1 параллелен графику функции y = k2x + b2, если k1 = k2.
Условие перпендикулярности двух прямых:
График функции y = k1x + b1 перпендикулярен графику функции y = k2x + b2, если k1k2 = −1 или k1 = −1/k2.
Точки пересечения графика функции y = kx + b с осями координат:
С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
Координаты точки пересечения с осью OY: (0; b).
С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.
Координаты точки пересечения с осью OX: (−b/k; 0).
Видео:Уравнение с двумя переменными и его график. Алгебра, 9 классСкачать

Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.
В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
Таким образом, нам надо построить график функции y = -4x — 10
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
Поставим эти точки в координатной плоскости и соединим прямой:
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.
Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
Вычтем из второго уравнения системы первое, и получим k = 3.
Подставим значение k в первое уравнение системы, и получим b = -2.
Ответ: уравнение прямой y = 3x — 2.
Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Тест по математике «Линейные уравнения с двумя переменными» (7 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 2 500 дидактических материалов для школьного и домашнего обучения
Тест. Линейные уравнения с двумя переменными
Решением уравнения -5х-3у- 1 = 0 являются пары чисел:
2. График уравнения 4х+2у-3 = 0 пересекает ось абсцисс в точке:
Из уравнения 2х-3у+4 =0 переменная у выражается через х формулой :
График уравнения у -9 = 0 на координатной плоскости расположен :
параллельно оси у и проходит через точку х = 9
параллельно оси у и проходит через точку х = -9
параллельно оси х и проходит через точку у = 9
параллельно оси х и проходит через точку у = -9
Изобразите схематично график уравнения, если известно, что это прямая, пересекающая ось у над осью х, и пересекающая ось х слева от оси у. Уравнение этой прямой:
Известно, что пара чисел (-2; 2) является решением уравнения 5х + ву — 4 = 0. Найдите в.
Ответ: 
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 710 человек из 76 регионов
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 859 человек из 77 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Сейчас обучается 48 человек из 21 региона
«Мотивация здорового образа жизни. Организация секций»
Свидетельство и скидка на обучение каждому участнику
- Для всех учеников 1-11 классов
и дошкольников - Интересные задания
по 16 предметам
«Как закрыть гештальт: практики и упражнения»
Свидетельство и скидка на обучение каждому участнику
Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 847 805 материалов в базе
Ищем педагогов в команду «Инфоурок»
Другие материалы
- 04.07.2017
- 586
- 1
- 04.07.2017
- 3434
- 214
- 04.07.2017
- 485
- 1
- 04.07.2017
- 1545
- 10
- 04.07.2017
- 285
- 0
- 04.07.2017
- 357
- 0
- 04.07.2017
- 496
- 2
«Учись, играя: эффективное обучение иностранным языкам дошкольников»
Свидетельство и скидка на обучение
каждому участнику
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 04.07.2017 4553
- DOCX 19.1 кбайт
- 69 скачиваний
- Рейтинг: 4 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Калинина Ирина Викторовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 6 месяцев
- Подписчики: 0
- Всего просмотров: 33147
- Всего материалов: 20
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Занятие 1. График линейной функции y=kx+bСкачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Эвакуированные в Россию из ДНР и ЛНР дети смогут поступить в вузы по квоте
Время чтения: 1 минута
Вузы РФ не будут повышать стоимость обучения на первом курсе
Время чтения: 1 минута
Минобрнауки РФ откроет центр по сбору учебников для школьников и студентов из ЛНР и ДНР
Время чтения: 2 минуты
Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу
Время чтения: 1 минута
Онлайн-семинар о здоровом образе жизни и организации секций
Время чтения: 2 минуты
Минпросвещения предлагает изменить форму для проведения ВОШ
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:ГРАФИК ЛИНЕЙНОГО УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСС видеоурокСкачать

Урок по теме «Уравнение касательной к графику» для 10-х классов с углубленным изучением математики
Разделы: Математика
Тема: Уравнение касательной к графику.
Цель урока: повторить теоретические знания по данной теме, закрепить их при решении задач.
Ход урока
1. Устная работа
1) Геометрический смысл производной.
— Если к графику функции у = f(x) в точке с абсциссой х0 можно провести касательную не параллельную оси Оу, то производная данной функции в точке х0 выражает угловой коэффициент касательной.
2) Записать формулу уравнения касательной.
у =
3) Известно, что угловой коэффициент касательной к графику функции в точке с абсциссой х0 равен 0,6. Чему равно значение производной в этой точке?

4) Касательная к графику функции f(x) в точке с абсциссой х0 образует с положительным направлением оси Ох угол 45 0 . Найдите значение производной в точке касания.

5) В каких точках кривой у = 2 – х 2 касательная к ней параллельна оси Ох.

6) Какой угол (острый или тупой ) образует с положительным направлением оси Ох касательная к графику функции в точке с абсциссой х0.
а) 
б) 
2. Проверка домашней работы.
Двое работают у доски во время устной работы.
3. Работа в группах.
Учитель выступает в роли консультанта. Порядок выполнения заданий не играет роли.
Задача 1. Найти угол между касательными к графику функции 
Решение: 




Задача 2. Является ли прямая у=х-1 касательной к кривой у=х 3 -2х+1?
Решение: Найдем общие точки графиков.
Воспользуемся схемой Горнера.
(1;0), (-2;-3) – общие точки.
Найдем угловые коэффициенты касательных в этих точках:

k1= 

Найдем уравнение касательной в точке (1;0)
Ответ: у=х-1 – касательная в точке (1;0) к графику функции у= х 3 -2х+1.
Задача 3. На параболе у=х 2 взяты две точки с абсциссами 1 и 3. Через эти точки проведена прямая. В какой точке параболы касательная будет параллельна проведенной прямой?
Решение: у=х 2 , (1;1), (3;9).
Найдем уравнение прямой 
Прямые параллельны, если их угловые коэффициенты равны.


Ответ: в точке (2;4) касательная параллельна заданной прямой.
Задача 4. Составить уравнение касательной к графику функции у=х 3 , х>0, отсекающей от осей координат треугольник, площадь которого равна 
Решение: Пусть (х0; у(х0)) — точка касания . Составим уравнение касательной у=х0 3 +3х0 2 (х-х0).
Найдем точки пересечения этой прямой с осями координат:

А(
ОВ = 2х0 3 ; ОА = 
Sтреуг = 
По условию х0 > 0 
Уравнение касательной у = 1 3 + 3*1 3 (х – 1).
4. Итог урока.
В – I.
1. Найдите уравнение касательной к графику функции 
А) у=-2х-3; Б) у= 2х-1; В) у= -2х+3; Г) у= 2х+3.
2. К графику функции у=3(х+2) проведены две параллельные касательные, одна из которых проходит через точку графика с абсциссой х0= — 1. Найдите абсциссу точки, в которой другая касательная касается графика данной функции.
А) — 2; Б) 2; В) 1; Г) — 3.
3. Напишите уравнение касательной к графику функции f(x) = x 2 – 4x + 5, если эта касательная проходит через точку (0; 4) и абсцисса точки касания положительна.
А) у = 2х+4; Б) у = -2х+4; В) у = -4х+4; Г) у = 4х-3.
В – II.
1. Найдите уравнение касательной к графику функции 
А) у =2х-6; Б) у = 10х+12; В) у= 4х+8; Г) у= -10х+8.
2. К графику функции у=-4(х-3) проведены две параллельные касательные, одна из которых проходит через точку графика с абсциссой х0= 1. Найдите абсциссу точки, в которой другая касательная касается графика данной функции.
А) — 1; Б) 5; В) 2; Г) — 3.
3. Напишите уравнение касательной к графику функции f(x) = x 2 + 3x + 5, если эта касательная проходит через точку (0; 1) и абсцисса точки касания отрицательна.
А) у = 2х+1; Б) у = х+1; В) у = -х+1; Г) у = -2х-5.
📽️ Видео
Урок ГРАФИК ЛИНЕЙНОЙ ФУНКЦИИ 7 КЛАСССкачать

2 часть ОГЭ по математике 2024 Вариант 1 ЯщенкоСкачать

Линейная функция и ее график. 7 класс.Скачать

График линейного уравнения с двумя переменными, 7 классСкачать

7 класс// АЛГЕБРА // График линейного уравнения с двумя переменнымиСкачать

Алгебра. 7 класс. Линейная функция. Урок 2 "Линейная функция"Скачать

График линейного уравнения. Алгебра 7 класс.Скачать

11. Прямая в пространстве и ее уравненияСкачать

№ 601-700 - Алгебра 8 класс КолягинСкачать

7 класс | УРОК №9 | Алгебра. Линейное уравнение с двумя переменными и его график.Скачать

Как построить график линейного уравнения с двумя переменными. Алгебра 7 класс.Скачать