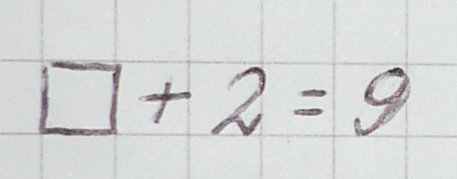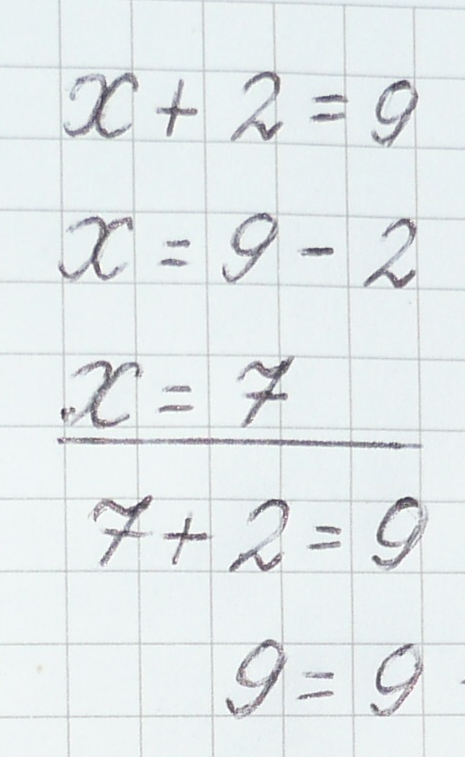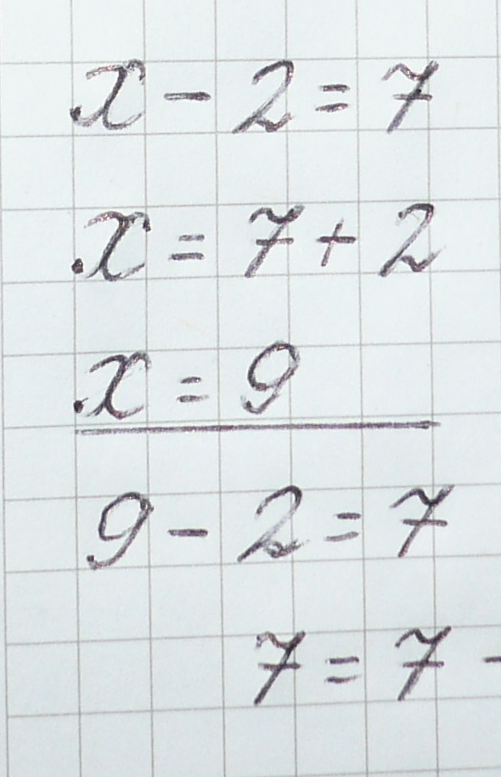Нужна ли проверка при решении уравнений (3 видео)

Начальные классы. Уравнения.

С уравнениями ученики знакомятся в 1 классе. Сначала решают примеры с окошком: выполняют действия с числами и задания на нахождение неизвестного числа, например было равенство:

И одно число решили спрятать:

Нам нужно догадаться, что за число спрятали?
Здесь прекрасно видно, чтобы найти неизвестное число, нужно из 9 — 2
Искомое число – 7.

В нашем равенстве – искомое число называют неизвестным числом.
А равенство, в котором одно число стало неизвестным, называется УРАВНЕНИЕМ.
Никто из вас никогда не видел, чтобы уравнения делали с «окошком». Это неудобно. Гораздо проще неизвестное обозначать буквами.

Неизвестное число обозначают маленькими латинскими буквами

или любой другой буквой.

И этому числу дают имя – корень уравнения.
Давайте посмотрим записи:
8+х
8+х>5
8+х =10
Только третья запись — уравнение. Потому что здесь есть неизвестное число и знак =.
Нам необходимо узнать это число.
Найти все значения х, при котором равенство будет верным — значит, решить уравнение, т.е. найти его корень.

При решении уравнения учитываем взаимосвязи между целым и частью:
— чтобы найти целое, надо сложить части;
— чтобы найти часть, надо из целого вычесть другую часть.

Если вы хотите более подробно узнать, как связаны целое и части, читайте тут.

Решение записывается так:

Корень пишем на следующей строке и подчеркиваем прямой линией.

Корень уравнения = 7, следовательно, наше уравнение решено.
Нам обязательно нужно проверить правильно мы нашли корень уравнения или нет.
Уравнение без проверки – это не уравнение.
Итак, в нашем уравнении корень –7, мы его подчеркнули, а теперь сделаем проверку. Для этого мы переписываем первую строку уравнения, но вместо неизвестного поставим значение корня.
Теперь: знак = пишем под знаком =. Число, записанное справа от знака равно: 9 – переписываем. Выражение, которое находится слева от знака равно: 7 + 2 – считаем. Получится 9. Это число 9 записываем слева от знака =.
Читаем выражение: 9 = 9. Значит, уравнение решили правильно.

Решим еще одно уравнение:

Ученикам начальной школы нужно обязательно овладеть математической речью. Для этого нужно знать, как называются компоненты при различных действиях, и как находится неизвестный компонент:

Если из суммы вычесть одно из слагаемых, то получится другое слагаемое.
Если к разности прибавить вычитаемое, то получится уменьшаемое.
Если из уменьшаемого вычесть разность, то получится вычитаемое.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 5 / 5. Количество оценок: 66

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Нужна ли проверка решения текстовой задачи?

С егодня все реже и реже в кругу преподавателей, методистов и репетиторов по математике возникают споры на около учебные методические темы. Одной из них является вопрос о необходимости обучения проверке в текстовых задачах. С приходом ЕГЭ по математике качественно изменилось содержание дискуссий вообще, и полемика о необходимости и правильности перехода на ЕГЭ перебила все рекорды по количеству споров и затмила собой все, что только можно затмить.

Однако, вопрос о проверке так и остался открытым. Для того, чтобы было понятно о чем пойдет дальше речь, давайте начнем с примера такой задачи: «В трех баках было всего 50л бензина, причем в первом баке было на литров больше, чем во втором. Когда из первого бака вылили в третий литров, во втором и третьем стало поровну. Сколько бензина было первоначально в первом баке?» Я много раз предлагал эту задачу ученикам-абитуриентам и даже репетиторам по математике. Обычно ответ поступал через несколько минут, а решение выглядело примерно так: пусть во втором баке было сначала х литров, тогда в первом баке было литров, а в третьем баке было литров. После переливания из первого бака в третий 26 литров в последнем стало литров. По условию задачи этот объем равен тому, который был во втором баке. Поэтому составим уравнение:

Решением уравнения будет х=22.
Большинство репетиторов по математике, школьных преподавателей и учеников, получив ответ в такой задаче, спрашивало: «ну и что же такого особенного в этой задаче?» И ожидаемая реплика : «решения нет» на удивление слышалась крайне редко.

Отшлифовки алгоритмов решения задач, которыми грешит современная школа, программируют и учеников и репетиторов. Предубеждение о том, что ответ в текстовой задаче непременно есть, начисто стирают из памяти привычку критически относиться к результатам решения.
Раньше, когда я еще учился в МПГУ, бушевали страсти по аккуратному использованию предлагаемых в школе алгоритмов и в одном из журналов «математика в школе» было напечатано письмо-вопрос учительницы Т.Н. Поляковой из Москвы под названием «нужна ли проверка при решении текстовых задач на составление уравнений?».

Тогда существовала такая странная точка зрения: проверка, мол состоит в том, что нужно составить новую задачу, в которой некоторое данное исходной задачи считается неизвестным, а прежнее неизвестное считается известным и решить новую задачу. Считалось, что тем самым проверяем, правильно ли было составлено само уравнение в исходной задаче. Непосвященный человек не поймет о чем идет речь, однако если другими словами сформулировать идею, то она будет звучать так: берется найденное значение неизвестной величины и считая его известным начальным данным прогоняется все условие задачи. Вычисляются все входящие величины, проверяется их соответствие смыслу задачи.

И действительно, если репетитору по математике подойти к вопросу с баками с точки зрения строгой логики, то , вообще то говоря, мы получили лишь то, что если решение задача имеет, то оно находится во множестве корней уравнения

Но вся суть в том, что «если имеется». А если его нет? Получаем классическое математическое условие-следствие. Любой репетитор по математике, профессионально занимающийся вопросами обучения решению задач с параметрами знает, что при получении ответа в алгоритме, построенном на следствии выполнения требований для параметра нужна обязательная проверка множества подчиняющихся этим требованиям параметры. Этот метод решения называется поиском необходимых условий. Удивительно, но почему-то ни один из таких профессиональных репетиторов по математике не догадался проверить ответ задачи на его соответствие условию. Странно, ведь в текстовой задаче мы имеем более простую интерпретацию общих законов логики.

В данном примере задачи на баки надо просто проверить, что при х=22 все переливания возможны и не приводят к появлению отрицательного количества литров в каком-нибудь из баков. Эту проверку число 22 не проходит. Следовательно, решений нет.

Ответ также можно проверить, накладывая переменную дополнительные ограничения в виде системы неравенств:

Очевидно, что второму условию не удовлетворяет.
Должен ли репетитор по математике, учитывая всеобщее снижение среднего уровня математической грамотности в стране и приходу ЕГЭ по математике еще и обучать делать проверку? Ведь текст задач по умолчанию предполагает наличие решения, а в бланк ответа текстовой задачи B12 на ЕГЭ никогда не придется записывать «нет» решений. Мне кажется, при неспешных занятиях хороший репетитор по математике должен показать хотя бы одну нестандартную задачу, например, про баки. После нее, возможно, кто-то из учеников начнет критически относиться к кажущимся очевидным математическим фактам, результат решений и выводам.

Колпаков Александр Николаевич, репетитор по математике.

Здравствуйте, Александр Николаевич. Я 6 лет назад случайно начала заниматься репетиторстом, после успешных занятий по математике, хороших отзывов учеников, решила более серьезно подойти к професии репетитора. 2 года, как собираю наработанный материал, читаю статьи по разным разделам математики. Спасибо, что Вы выставляете свой наработанный материал на всеобщее чтение, побольше бы таких статей и ученики, и учителя были бы более грамотными…

Подвох заметен уже при разборе условия: после перелива в третьем баке как минимум 26 литров, и столько же во втором. Вместе больше 50 — решения быть не может.

А тема хорошая, хотя бы минимальная привычка обдумать и проверить результат должна быть. Любой может ошибиться даже на ровном месте, значит разумно подстраховаться, проверить свои действия.

Так что от целенаправленного обучения проверке репетитору по математике никак не уйти.

Видео:Простые уравнения. Как решать простые уравнения?Скачать

Уравнение. Проверка решения уравнения

Тема: Уравнение. Проверка решения уравнения.

Предметная цель: сформировать умение выполнять проверку решения уравнения, научить составлять уравнение к задаче.

Метапредметные цели: формирование УУД:
• Регулятивные: формировать способность принимать учебную цель и задачу, выдвигать гипотезы, планировать ее реализацию, контролировать и оценивать свои действия, действия своих товарищей, проявлять инициативность, самостоятельность.
• Познавательные: формировать способность воспринимать и анализировать небольшие тексты, использовать знаково-символьные средства, в том числе действие моделирования, выполнять логические операции, работать с информацией: поиск в Интернете, энциклопедии, в наборе гербария, преобразовывать информацию, формулировать тему и цель урока.
• Коммуникативные: формировать умение учитывать позицию собеседника, осуществлять сотрудничество и кооперацию с учителем и сверстниками, адекватно воспринимать и передавать информацию.

• Личностные: формировать учебно-познавательный интерес к новому материалу и способу решения новой задачи, умение оценивать свою работу и работу своих товарищей, воспитывать ответственность за свою работу, развивать мотивацию к учению и познанию, готовность и способность к саморазвитию, развитие толерантности.

Оборудование: Мультимедийный проектор, компьютер для учителя, экран, карточки с ребусами, рабочие странички для работы в группах, рабочие странички для домашнего задания, учебная презентация, аудиозапись.

Этапы урока. Содержание этапа.

I. Организационный момент. (1 минута)

— Нас снова встречает царица наук Математика. Давайте скажем приятные слова для неё. (слайд № 1)

Чтоб водить корабли,

Чтобы в небо взлететь,

Надо многое знать,

Надо много уметь!

И при этом, и при этом

Очень важная наука –

II. Эмоциональное вхождение в урок. (1 минута)

— Дорогие ребята, царица Математика приготовила для вас сюрприз: каждый из вас под столом его найдёт. (к крышке стола прикреплен цветной магнит)

— Это кнопка управления. На счёт три нажимайте на неё.

(звучит аудиозапись с обращением царицы Математики)

— Дорогие умники и умницы! Вы путешествовали по загадочной стране Уравнений. Как вы думаете, можно ли еще узнать что-то новое о жителях этой страны об уравнениях? Хотите продолжить путешествие? Итак, в путь!

III. Установка на мотивацию. (1 минута)

— Ребята, наши друзья Вова, Катя и Петя путешествовали по этой стране и заблудились.( Слайд № 2) Хотите им помочь? А как им можно помочь?

— Да, надо преодолеть все математические препятствия. Вы готовы?

— А какими мы должны быть, чтобы у нас всё получилось?

— Итак, начнём, ведь наши друзья ждут от нас помощи.

IV. Актуализация знаний ( 7 минут) (Учитель предлагает ученикам самим сформулировать каждое задание. После выполнения каждого задания дети дают самооценку и взаимооценку)

Начертить к уравнению схему и решить его (работа в парах по карточкам)

— Дети, давайте вспомним о правилах работы в паре.

х – 2 = 8