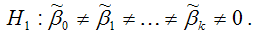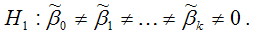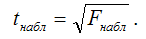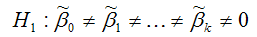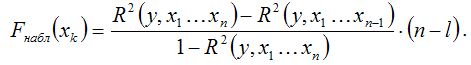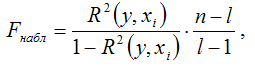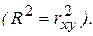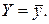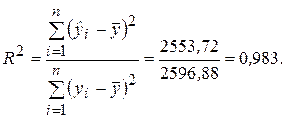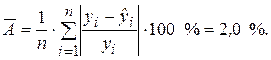Нулевая гипотеза о статистической незначимости уравнения регрессии отклоняется если (2 видео)

Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом

Проверка значимости коэффициентов регрессии означает проверку основной гипотезы об их значимом отличии от нуля.

Основная гипотеза состоит в предположении о незначимости коэффициентов модели множественной регрессии, т. е.

Обратная или конкурирующая гипотеза состоит в предположении о значимости коэффициентов модели множественной регрессии, т. е.

Данные гипотезы проверяются с помощью t-критерия Стьюдента, который вычисляется посредством частного F-критерия Фишера-Снедекора.

При проверке основной гипотезы о значимости коэффициентов модели множественной регрессии применяется зависимость, которая существует между t-критерием Стьюдента и частным F-критерием Фишера-Снедекора:

При проверке значимости коэффициентов модели множественной регрессии критическое значение t-критерия определяется как tкрит(а;n-l-1), где а – уровень значимости, n – объём выборочной совокупности, l – число оцениваемых по выборке параметров, (n-l-1) – число степеней свободы, которое определяется по таблице распределений t-критерия Стьюдента.

При проверке основной гипотезы вида

наблюдаемое значение частного F-критерия Фишера-Снедекора рассчитывается по формуле:

При проверке основной гипотезы возможны следующие ситуации.

Если наблюдаемое значение t-критерия больше критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е.

tнабл≥tкрит, то основная гипотеза о незначимости коэффициента βk модели множественной регрессии отвергается, и он является значимым.

Если наблюдаемое значение t-критерия меньше критического значения t-критерия (определённого по таблице распределения Стьюдента), т.е. tнабл , то основная гипотеза о незначимости коэффициента βk модели множественной регрессии принимается.

Проверка основной гипотезы о значимости модели множественной регрессии в целом состоит в проверке гипотезы о значимости коэффициента множественной корреляции или значимости параметров модели регрессии.

Если проверка значимости модели множественной регрессии в целом осуществляется через проверку гипотезы о значимости коэффициента множественно корреляции, то выдвигается основная гипотеза вида Н₀:R(y,x_i)=0, утверждающая, что коэффициент множественной корреляции является незначимым, и, следовательно, модель множественной регрессии в целом также является незначимой.

Обратная или конкурирующая гипотеза вида Н₁:R(y,x_i)≠0 утверждает, что коэффициент множественной корреляции является значимым, и, следовательно, модель множественной регрессии в целом также является значимой.

Данные гипотезы проверяются с помощью F-критерия Фишера-Снедекора.

Наблюдаемое значение F-критерия (вычисленное на основе выборочных данных) сравнивают со значением F-критерия, которое определяется по таблице распределения Фишера-Снедекора, и называется критическим.

При проверке значимости коэффициента множественной корреляции критическое значение F-критерия определяется как Fкрит(a;k1;k2), где а – уровень значимости, k1=l–1 и k2=n–l – число степеней свободы, n – объём выборочной совокупности, l – число оцениваемых по выборке параметров.

При проверке основной гипотезы вида Н₀:R(y,x_i наблюдаемое значение F-критерия Фишера-Снедекора рассчитывается по формуле:

где R 2 (y,x_i) – коэффициент множественный детерминации.

При проверке основной гипотезы возможны следующие ситуации.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) больше критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл>Fкрит, то с вероятностью а основная гипотеза о незначимости коэффициента множественной корреляции отвергается, и он признаётся значимым. Следовательно, модель множественной регрессии в целом также является значимой.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) меньше или равно критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т.е. Fнабл≤Fкрит, то основная гипотеза о незначимости коэффициента множественной корреляции принимается, и он признаётся незначимым. В этом случае модель множественной регрессии признаётся незначимой.

Видео:Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Анализ общего качества уравнения регрессии.

Коэффициент детерминации R 2

После проверки точности и статистической значимости каждого коэффициента регрессионной модели обычно проводится анализ общего качества уравнения модели, которое оценивается по тому, как хорошо эмпирическое уравнение регрессии согласуется со статистическими данными. Другими словами, необходимо оценить, насколько широко рассеяны точки наблюдений по их совокупности относительно линии регрессии (линии модели). Поэтому представляется естественным вывод о том, что проверку общего качества регрессионной модели следует проводить на основе дисперсионного анализа, сравнивая дисперсии модельных и реальных значений исследуемой переменной Y.

Рассмотрим для определенного набора наблюдений n дисперсию D_n(y), которая характеризует разброс значений y_i вокруг среднего значения. Из дисперсионного анализа следует, что эту дисперсию можно разбить на две части: объясняемую уравнением регрессии и не объясняемую (т. е. связанную со случайными отклонениями e_i). Тогда выполняется следующее соотношение:

(2.27)

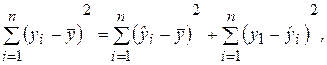
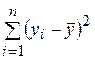
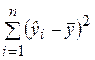
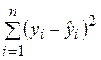
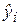
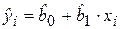
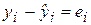
где – общая сумма квадратов отклонений зависимой переменной Y от среднего значения;

– сумма квадратов, объясняемая уравнением регрессии;

– необъясненная (остаточная) сумма квадратов. Напомним, что определяется как , а .

Разделив выражение (2.27) на его левую часть, получим формулу для оценки характеристики, которая обозначается как R 2 и называется коэффициентом детерминации:

(2.28)

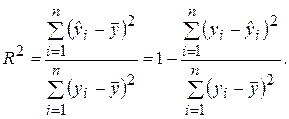
Коэффициент детерминации R 2 является мерой качества уравнения регрессионной модели и определяет долю дисперсии (разброса), объясняемую регрессией Y на Х, в общей дисперсии зависимой переменной Y.

Из проведенных рассуждений следует, что R 2 принимает значения между 0 и 1 (0 £ R 2 £ 1). Чем ближе R 2 к единице, тем теснее линейная связь между Х и Y (экспериментальные точки теснее примыкают к линии регрессии). Чем ближе R 2 к нулю, тем такая связь слабее. Если R 2 = 0, то дисперсия зависимой переменной полностью обусловлена воздействием неучтенных факторов и линия регрессии (модели) должна быть параллельна оси абсцисс (Y = ).

Например, если для построенной модели R 2 = 0,7, то согласно (2.28) можно утверждать, что поведение зависимой переменной (результативного признака) Y на 70 % объясняется влиянием фактора Х и на 30 % обусловлено влиянием неучтенных факторов. Доля влияния неучтенных факторов связана со случайными отклонениями e_i и определяется отношением 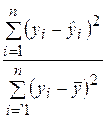, характеризующим долю разброса зависимой переменной, не объясняемую линейной регрессией Y на Х.

Естественно, что для исследуемого объекта наиболее качественной будет считаться модель с наибольшим значением коэффициента детерминации R 2 .

Заметим, что коэффициент детерминации имеет смысл рассматривать только при наличии параметра 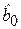(свободного члена) в уравнении регрессионной модели.

Таким образом, коэффициент детерминации R 2 определяет степень тесноты статистической связи между Y и Х. Но об этом же говорит выборочный коэффициент корреляции r_xy. Рассматривая эти характеристики, можно установить, что в случае парной линейной регрессионной модели коэффициент детерминации равен квадрату коэффициента корреляции

Действительно, учитывая (2.13),

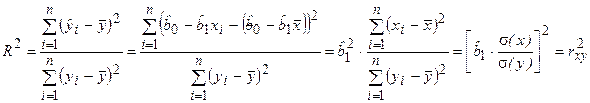
Естественно, возникает вопрос, какое значение R 2 можно считать удовлетворительным. Ответ на этот вопрос может быть неоднозначным, особенно в случае множественной регрессионной модели и зависит от объема выборки n и постановки задачи, вытекающей из предмодельного анализа.

Более точно проверить значимость уравнения регрессии, т. е. установить, соответствует ли построенная модель реальным данным и достаточно ли включенных в уравнение объясняющих переменных для описания зависимой переменной, позволяет F-тест, который проводится по схеме статистической проверки гипотез. Тестируется гипотеза Н₀ о статистической незначимости уравнения регрессии.

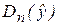
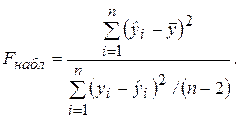
Рассмотрим «объясненную» и «необъясненную» дисперсии: и D_n(e). Отношение этих дисперсий, рассчитанное на одну степень свободы, имеет F-распределение (F-статистику), фактически наблюдаемое значение которой для парной регрессии определяется формулой

(2.29)

Учитывая смысл дисперсий 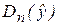и D_n(e), можно считать, что значение F_набл показывает, в какой мере уравнение регрессии лучше оценивает значение зависимой переменной по сравнению с

Согласно схеме статистической проверки гипотез, гипотеза Н₀ отклоняется, т. е. признается статистическая значимость и надежность уравнения регрессии на заданном уровне α, если F_набл превосходит критическое (табличное) значение F-статистики Фишера (F_набл > F_кр = F_α, 1, n — 2). Если F_набл 2 . В этом случае гипотеза Н₀ о статистической незначимости регрессионной модели заменяется эквивалентной гипотезой о статистической незначимости R 2 .

Для парной регрессионной модели способы проверки значимости коэффициента 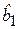с использованием t-критерия (t-тест) и уравнения регрессии (показателя тесноты связи R 2 ) с использованием F-критерия равносильны, поскольку эти критерии связаны соотношением F = t 2 .

Наряду с коэффициентом детерминации R 2 для оценки качества парной регрессионной модели можно использовать характеристику, называемую средней ошибкой аппроксимации :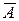

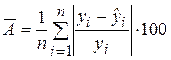
%. (2.31)

Средняя ошибка аппроксимации определяет среднее относительное отклонение расчетных данных (оцененных по уравнению модели) от фактических. 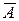является безразмерной величиной и обычно выражается в процентах. Принято считать, что качество модели считается удовлетворительным, если средняя ошибка аппроксимации не превышает 8-9 %.

Пример 2.3.Проверить общее качество и статистическую значимость уравнения регрессии для модели, построенной в примере 2.1.

Оценку качества построенной модели дают коэффициент детерминации R 2 и средняя ошибка аппроксимации .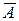

Вычислим коэффициент детерминации, воспользовавшись данными табл. 2.1.

Величина коэффициента детерминации показывает, что поведение результативного признака (недельного потребления) Y на 98,3 % объясняется влиянием фактора Х (изменением недельного дохода), а остальные 1,7 % составляют долю необъясненной вариации, происходящей под действием прочих (неучтенных) факторов.

Расчет средней ошибки аппроксимации представлен в последнем столбце табл. 2.1.

Рассчитанные значения коэффициента детерминации и средней ошибки аппроксимации свидетельствуют о достаточно высоком общем качестве построенной модели.

Проверим статистическую значимость уравнения регрессионной модели с помощью F-теста. Расчетное (наблюдаемое) значение F-статистики Фишера вычисляется по формуле:

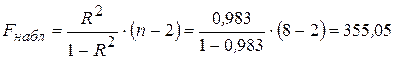
Табличное значение F-статистики при уровне значимости α = 0,01 и числе степеней свободы ν = n – 2 будет составлять 13,75 (F_кр = 13,75).

Так как F_набл > F_кр (355,05 > 13,75), то нулевая гипотеза Н₀ отклоняется и уравнение регрессионной модели признается статистически значимым и весьма надежным, поскольку наблюдаемое значение F-статистики превосходит табличное значение критерия более чем в 25 раз.

Дата добавления: 2016-06-02 ; просмотров: 2288 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Коварный t критерий СтьюдентаСкачать

Проверка значимости модели множественной регрессии и ее параметров

Для оценки значимости параметров уравнения множественной регрессии используют критерий Стьюдента. Напомним, что значимость параметров означает их отличие от нуля с высокой долей вероятности. Нулевой гипотезой в данном случае является утверждение

Фактическое значение t-критерия определяется по формуле

(2.27)

В формуле (2.27) под оценкой параметра понимается как коэффициент регрессии, так и свободный член (при ). Величина среднего квадратического отклонения оцениваемого параметра определяется как корень из дисперсии , рассчитанной по формуле (2.25). Величину называют стандартной ошибкой параметра .

Формулу для оценки коэффициента регрессии (т.е. для ) можно привести к виду

(2.28)

где – среднее квадратическое отклонение результативной переменной ; – среднее квадратическое отклонение объясняющей переменной , являющейся сомножителем коэффициента ; – коэффициент детерминации, найденный для уравнения зависимости переменной от переменных , включая ; – коэффициент детерминации, найденный для уравнения зависимости переменной от других переменных , входящих в рассматриваемую модель множественной регрессии.

Теоретическое значение t-критерия находят по таблице значений критерия Стьюдента для уровня значимости а и числа степеней свободы . Уровень значимости а представляет собой вероятность ошибки первого рода, т.е. вероятность отвергнуть гипотезу , когда она верна. Как правило, а выбирают равным 0,1; 0,05 или 0,01.

Нулевая гипотеза о незначимости параметра : отвергается, если выполняется неравенство

(2.29)

где – теоретическое значение критерия Стьюдента.

На основе выражения (2.29) можно построить также доверительный интервал для оцениваемого параметра :

(2.30)

Выражение (2.30) позволяет как оценить значимость параметра, так и дать его экономическую интерпретацию (если оценивается коэффициент регрессии). Очевидно, что параметр будет значим, если в доверительный интервал (2.30) не входит нуль, т.е. с большой долей вероятности оцениваемый параметр не равен нулю.

Так как коэффициент регрессии является абсолютным показателем силы связи, границы доверительного интервала и для него также можно интерпретировать аналогичным образом: с вероятностью при единичном изменении независимой переменной зависимая переменная у изменится не меньше, чем на , и не больше, чем на .

Рассмотрим результаты оценки значимости параметров для примера 2.1. Стандартные ошибки параметров равны

Напомним, что под знаком корня в квадратных скобках стоит элемент матрицы , который находится на пересече-

нии j-й строки и j-го столбца, номер; равен номеру оцениваемого параметра.

Фактическое значение критерия Стьюдента равно

Табличное значение t-критерия для и уровне значимостисоставляет 2,0153, следовательно, все параметры, кроме свободного члена, значимы .

Найдем границы доверительных интервалов для коэффициентов регрессии.

Отметим, что, руководствуясь значениями границ доверительных интервалов, можно сделать те же выводы о значимости коэффициентов регрессии (так как нуль не попадает в доверительный интервал). Выводы в данном случае и не могли быть иными, чем при сравнении фактического и табличного значений критерия Стьюдента, так как формула (2.30) является следствием формулы (2.29). Дадим экономическую интерпретацию границ доверительных интервалов для коэффициентов регрессии.

Коэффициент является характеристикой силы связи между объемом поступления налогов и количеством занятых. С учетом значений границ доверительного интервала дляможно сказать, что изменение количества занятых на 1 тыс. человек приведет к изменению (с вероятностью 0,95 ()) поступления налогов не менее чем на 3,56 млн руб. и не более чем на 21,34 млн руб. при неизменном объеме отгрузки в обрабатывающих производствах и производстве энергии. Для двух других коэффициентов регрессии выводы будут следующими.

Изменение объема отгрузки в обрабатывающих производствах на 1 млн руб. приведет к изменению (с вероятностью 0,95 ()) поступления налогов не менее чем на 0,028 млн руб. и не более чем на 0,092 млн руб. при неизменных значениях количества занятых и производства энергии.

При изменении производства энергии на 1 млн руб. поступление налогов изменится (с вероятностью 0,95 ()) не менее чем на 0,13 млн руб. и не более чем на 0,18 млн руб. при неизменных значениях количества занятых и объема отгрузки в обрабатывающих производствах.

Как было отмечено в параграфе 2.2, при построении модели регрессии с использованием центрированных переменных коэффициенты регрессии не отличаются от коэффициентов регрессии в натуральной форме. Это утверждение относится также к величине стандартных ошибок коэффициентов регрессии и, следовательно, к фактическим значениям критерия Стьюдента.

При использовании стандартизованных переменных меняется масштаб их измерения, что приводит к другим, чем в исходной регрессии, значениям параметров (стандартизованных коэффициентов регрессии) и их стандартных ошибок. Однако фактические значения критерия Стьюдента для параметров уравнения в стандартизованном масштабе совпадают с теми значениями, которые были получены по уравнению в натуральном масштабе.

Для оценки значимости всего уравнения регрессии в целом используется критерий Фишера (F-критерий), который в данном случае называют также общим F-критерием. Под незначимостью уравнения регрессии понимается одновременное равенство нулю (с высокой долей вероятности) всех коэффициентов регрессии в генеральной совокупности:

Фактическое значение F-критерия определяется как соотношение факторной и остаточной сумм квадратов, рассчитанных по уравнению регрессии и скорректированных на число степеней свободы:

(2.31)

где – факторная сумма квадратов; – остаточная сумма квадратов.

Теоретическое значение F-критерия находят по таблице значений критерия Фишера для уровня значимости α, числа степеней свободы и . Нулевая гипотеза отвергается, если

где – теоретическое значение критерия Фишера.

Отметим, что если модель незначима, то незначимы и показатели корреляции, рассчитанные по ней. Действительно, если

то

и линия регрессии параллельна оси абсцисс. Кроме того, из системы нормальных уравнений, полученной по методу наименьших квадратов (2.8), следует, что .

При нулевых значения всех коэффициентов регрессии имеем выражение

т.е. при равенстве всех коэффициентов регрессии нулю (их статистической незначимости) коэффициент детерминации также будет равен нулю (статистически незначим).

Формулу (2.31) расчета F-критерия можно преобразовать, разделив факторную и остаточную суммы квадратов на общую сумму квадратов:

После простых преобразований получаем выражение

Расчет общего F-критерия можно оформить в виде таблицы дисперсионного анализа (табл. 2.2).

Таблица 2.2. Анализ статистической значимости модели множественной регрессии

Число степеней свободы df

Сумма квадратов SS

Дисперсия на одну степень свободы MS = SS/df

табличное значение для а = 0,05

Аналогичную таблицу дисперсионного анализа можно увидеть в результатах компьютерной обработки данных. Ее отличие

от приведенной выше таблицы заключается в содержании последнего столбца. В нашем случае это теоретическое значение критерия Фишера. В компьютерных вариантах в последнем столбце приводится значение вероятности допустить ошибку первого рода (отвергнуть верную нулевую гипотезу), которая соответствует фактическому значению F-критерия. В Excel эта величина называется «значимость F». Обозначим величину, выдаваемую компьютером в таблице дисперсионного анализа, как . Ее значение можно проинтерпретировать следующим образом: если теоретическое значение F-критерия равно его фактическому значению, то вероятность ошибки первого рода (уровень значимости) равна .

Выбирая для определения табличного значения критерия некий уровень значимости, мы соглашаемся на величину ошибки, равную. Следовательно, если , то фактическая ошибка будет меньше запланированной и можно говорить о значимости уравнения регрессии при заданном уровне значимости .

Проверим на статистическую значимость уравнение регрессии, полученное в примере 2.1. Фактическое значение F-критерия равно

Табличное значение критерия Фишера для а = 0,05, числа степеней свободы и равно 2,82. Так как фактическое значение F-критерия больше табличного, уравнение регрессии значимо с вероятностью Следовательно, значим также коэффициент детерминации, т.е. он с большой долей вероятности отличен от нуля.