Этот онлайн калькулятор позволит вам очень просто найти параметрическое и каноническое уравнение прямой проходящей через две точки.
Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на составление уравнения прямой и закрепить пройденный материал.
- Найти уравнение прямой
- Ввод данных в калькулятор для составления уравнения прямой
- Дополнительные возможности калькулятора для составления уравнения прямой
- Теория. Уравнение прямой.
- Нормальное уравнение прямой
- Приведение общего уравнения прямой на плоскости к нормальному виду
- Нормальное (нормированное) уравнение прямой: описание, примеры, решение задач
- Нормальное уравнение прямой – описание и пример
- Приведение общего уравнения прямой к нормальному виду
- 📹 Видео
Видео:Видеоурок "Нормальное уравнение прямой"Скачать

Найти уравнение прямой
Выберите необходимую вам размерность:
Введите координаты точек.
Ввод данных в калькулятор для составления уравнения прямой
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для составления уравнения прямой
- Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.
Теория. Уравнение прямой.
Прямая — один из базовых элементов геометрии. Используя уравнения прямых можно существенно упростить решение многих задач.
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:9 класс, 7 урок, Уравнение прямойСкачать

Нормальное уравнение прямой
В данной статье мы рассмотрим нормальное уравнение прямой на плоскости. Приведем примеры построения нормального уравнения прямой по углу наклона нормального вектора прямой от оси Ox и по расстоянию от начала координат до прямой. Представим метод приведения общего уравнения прямой к нормальному виду. Рассмотрим численные примеры.
Пусть на плоскости задана декартова прямоугольная система координат. Тогда нормальное уравнение прямой L на плоскости представляется следующей формулой:
| xcosφ+ysinφ−r=0, | (1) |
где r− расстояние от начала координат до прямой L, а φ− это угол между нормальным вектором n прямой L и осью Ox. (Если r>0, то нормальный вектор n направлен в сторону прямой L).
Выведем формулу (1). Пусть на плоскости задана декартова прямоугольная система координат и прямая L (Рис.1). Проведем через начало координат прямую Q, перпендикулярную прямой L, и точку пересечения обозначим через R. На этой прямой выделим единичный вектор n, с направлением, совпадающим с вектором 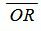
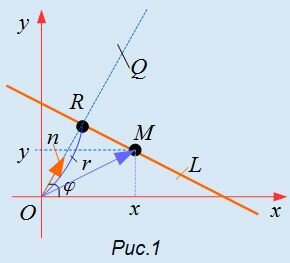 |
Выразим уравнение прямой L через два параметра: длину отрезка 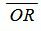
Так как вектор n является единичным вектором, то его проекции на Ox и Oy будут иметь следующие координаты:
| n=<cosφ, sinφ>. | (2) |
Обозначим через r расстояние от начала координат до точки R. Рассмотрим, теперь, точку M(x,y). Точка M лежит на прямой L тогда и только тогда, когда проекция вектора 
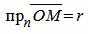 | (3) |
Скалярное произведение векторов n и 
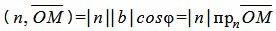 , , | (4) |
где 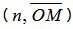


Поскольку n единичный вектор, то (4) можно записать так:
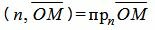 . . | (5) |
Учитывая, что n=<cosφ, sinφ>, 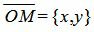
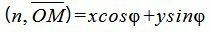 . . | (6) |
Тогда из уравнений (3), (5), (6) следует:
| xcosφ+ysinφ=r |
| xcosφ+ysinφ−r=0. | (7) |
Мы получили нормальное уравнение прямой L. Уравнение (7) (или (1)) называется также нормированным уравнением прямой .
Пример 1. Построить нормальное уравнение прямой, нормальный вектор которого с осью Ox имеет угол φ=60°, а расстояние от начала координат до прямой составляет 4.
Решение. Имеем: φ=60°, r=4. Вычисляем:
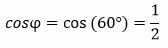 , , 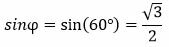 |
Подставляя вычисленные значения в (7) получим:
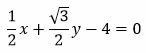 . . |
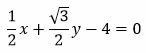 . . |
Видео:Нормальное уравнение прямой на плоскостиСкачать

Приведение общего уравнения прямой на плоскости к нормальному виду
Так как уравнения (1) и (8) должны определять одну и ту же прямую (Замечание 1 статьи «Общее уравнение прямой на плоскости»), то существует такое число t, что
| tAx=cosφ, tB=sinφ, tC=−r. | (9) |
Возвышая в квадрат первые два равенства в (9) и складывая их, получим:
| (tA) 2 +(tB) 2 =cos 2 φ+sin 2 φ=1. | (10) |
Упростим выражение и найдем t:
| t 2 A 2 +t 2 B 2 =t 2 (A 2 +B 2 )=1, |
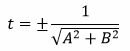 . . | (11) |
Знаменатель в (11) отличен от нуля, т.к. хотя бы один из коэффициентов A, B не равен нулю (в противном случае (8) не представлял бы уравнение прямой).
Выясним, какой знак имеет t. Обратим внимание на третье равенство в (9). Так как r−это расстояние от начала координат до прямой, то r≥0. Тогда произведение tC должна иметь отрицательный знак. Т.е. знак t в (11) должен быть противоположным знаку C.
Подставляя в (1) вместо cosφ, sinφ, и −r значения из (9), получим tAx+tBy+tC=0. Т.е. для приведения общего уравенения прямой к нормальному виду, нужно заданное уравнение умножить на множитель (11). Множитель (11) называется нормирующим множителем .
Пример 2. Задано общее уравнение прямой
Построить нормальное уравнение прямой.
Решение. Из уравнения (12) можно записать: A=2, B=−3, C=4. Вычислим t из равенства (11):
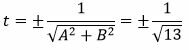 |
Так как C>0, то знак t отрицательный:
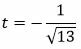 |
Умножим уравнение (12) на t:
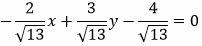 |
Ответ. Нормальное уравнение прямой (12) имеет следующий вид:
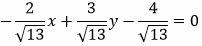 |
Отметим, что число 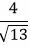
Видео:5. Нормальное уравнение плоскости выводСкачать

Нормальное (нормированное) уравнение прямой: описание, примеры, решение задач
В данной статье рассмотрим нормальное уравнение прямой на заданной плоскости. Получим нормальное уравнение, покажем не примере, дадим определение нормирующего множителя и разберем приведение общего уравнения к нормальному виду. Заключительной части посвятим основному приложению нормального уравнения прямой, то есть нахождение расстояние от точки до прямой на плоскости.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Нормальное уравнение прямой – описание и пример
Рассмотрим выведение нормального уравнения.
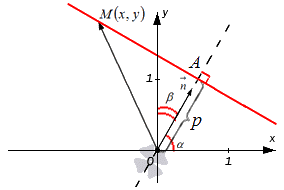
Фиксируем на плоскости систему координат О х у , где задаем прямую с точкой, через которую она проходит с нормальным вектором прямой. Нормальному вектору прямой дадим обозначение n → . Его начало обозначено точкой O . координатами являются cos α и cos β , углы которых расположены между вектором n → и положительными осями О x и O y . Это запишется так: n → = ( cos α , cos β ) . Прямая проходит через точку A с расстоянием равным p , где p ≥ 0 от начальной точки O при положительном направлении вектора n → . Если р = 0 , тогда A считается совпадающей с точкой координат. Отсюда имеем, что O A = p . Получаем уравнение, при помощи которого задается прямая.
Имеем, что точка с координатами M ( x , y ) расположена на прямой тогда и только тогда, когда числовая проекция вектора O M → по направлению вектора n → равняется p , значит при выполнении условия n p n → O M → = p .
O M → является радиус-вектором точки с координатами M ( x , y ) , значит O M → = ( x , y ) .
Применив определение скалярного произведения векторов, получим равенство вида: n → , O M → = n → · n p n → O M → = 1 · n p n → O M → = n p n → O M → = p
Тогда это же произведение будет иметь вид в координатной форме: n → , O M → = cos α · x + cos β · y
Отсюда cos α · x + cos β · y = p или cos α · x + cos β · y — p = 0 . Было выведено нормальное уравнение прямой.
Уравнение вида cos α · x + cos β · y — p = 0 называется нормальным уравнением прямой или нормированным уравнением прямой. Иначе говоря, уравнение прямой в нормальном виде.
Понятно, что такое уравнение представляет собой общее уравнение прямой A x + B y + C = 0 , где A и B имеют значения, при которых длина вектора n → = ( A , B ) равна 1 , а C является неотрицательным числом.
Теперь рассмотрим его геометрический смысл. Нормальное уравнение прямой вида cos α · x + cos β · y — p = 0 задает в системе координат О х у на плоскости прямую с наличием нормального вектора единичной длины n → = ( cos α , cos β ) , которая располагается на расстоянии равном p от начала координат по положительному направлению вектора n → .
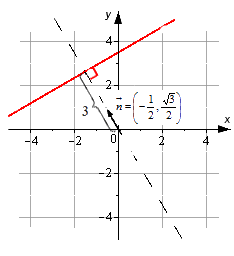
Если дано уравнение прямой вида — 1 2 · x + 3 2 · y — 3 = 0 , то на плоскости задается прямая, у которой нормальный вектор с координатами — 1 2 , 3 2 . Удаление прямой от начала координат идет по направлению, совпадающему с направлением нормального вектора n → = — 1 2 , 3 2 .
Видео:§13 Нормальное уравнение прямойСкачать

Приведение общего уравнения прямой к нормальному виду
Часто решение задач подразумевает использование нормального уравнения прямой, но само оно не дается в нормальном виде, поэтому необходимо для начала приводить к нормальному виду, после чего выполнять необходимые вычисления.
Нормальное уравнение получают из общего уравнения прямой. Когда на плоскости задается другим уравнением, то необходимо привести его к общему виду, после чего возможно приведение к нормальному. Если рассмотреть на примере, то это будет выглядеть так.
Для приведения общего уравнения прямой A x + B x + C = 0 к нормальному необходимо обе части умножить на нормирующий множитель, который имеет значение ± 1 A 2 + B 2 . Его знак определяется при помощи противоположности знака слагаемого C . При С = 0 знак выбирается произвольно.
Привести уравнение прямой 3 x — 4 y — 16 = 0 к нормальному виду.
Из общего уравнения видно, что А = 3 , В = — 4 , С = — 16 . Так как значение C отрицательное, необходимо брать положительный знак для формулы. Перейдем к вычислению нормирующего множителя:
1 A 2 + B 2 = 1 3 2 + ( — 4 ) 2 = 1 5
Теперь необходимо умножить обе части уравнения на одну пятую. Получим, что 1 5 · ( 3 x — 4 y — 16 ) = 0 ⇔ 3 5 · x — 4 5 · y — 16 5 = 0 .
Нормальное уравнение по заданной прямой найдено.
Ответ: 3 5 · x — 4 5 · y — 16 5 = 0 .
📹 Видео
Лекция 23. Виды уравнений прямой на плоскости.Скачать

Видеоурок "Общее уравнение прямой"Скачать

Нормальное уравнение прямой.Вывод нормального уравнения прямой.Скачать

Нормальное (нормированное) уравнение прямойСкачать

УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать

Уравнения прямой на плоскости | Векторная алгебраСкачать

Уравнение прямой на плоскостиСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Уравнение прямой на плоскости. Решение задачСкачать

Математика это не ИсламСкачать