Нормальное псевдорешение системы линейных уравнений (7 видео)

VMath

Содержание

Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Метод наименьших квадратов
Влияние систематических ошибок
Псевдорешение системы линейных уравнений
Геометрическая интерпретация
Псевдообратная матрица
Источники
Псевдорешения системы линейных уравнений
Алгоритм нахождения псевдорешения неоднородной системы
🎬 Видео

Инструменты сайта

Основное

Информация

Действия

Содержание

Вспомогательная страница к разделу ☞ ИНТЕРПОЛЯЦИЯ.

Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Метод наименьших квадратов

Пусть из физических соображений можно считать (предполагать), что величины $ x_ $ и $ y_ $ связаны линейной зависимостью вида $ y=kx+b $, а неизвестные коэффициенты $ k_ $ и $ b_ $ должны быть оценены экспериментально. Экспериментальные данные представляют собой $ m>1 $ точек на координатной плоскости $ (x_1,y_1), dots, (x_m,y_m) $. Если бы эти опыты производились без погрешностей, то подстановка данных в уравнение приводила бы нас к системе из $ m_ $ линейных уравнений для двух неизвестных $ k_ $ и $ b_ $: $$ y_1=k,x_1+b, dots, y_m=k,x_m+b . $$ Из любой пары уравнений этой системы можно было бы однозначно определить коэффициенты $ k_ $ и $ b_ $.

Однако, в реальной жизни опытов без погрешностей не бывает

Дорогая редакция! Формулировку закона Ома следует уточнить следующим образом:«Если использовать тщательно отобранные и безупречно подготовленные исходные материалы, то при наличии некоторого навыка из них можно сконструировать электрическую цепь, для которой измерения отношения тока к напряжению, даже если они проводятся в течение ограниченного времени, дают значения, которые после введения соответствующих поправок оказываются равными постоянной величине».

Источник: А.М.Б.Розен. Физики шутят. М.Мир.1993.

Будем предполагать, что величины $ x_,dots,x_m $ известны точно, а им соответствующие $ y_1,dots,y_m $ — приближенно. Если $ m>2 $, то при любых различных $ x_ $ и $ x_j $ пара точек $ (x_,y_i) $ и $ (x_,y_j) $ определяет прямую. Но другая пара точек определяет другую прямую, и у нас нет оснований выбрать какую-нибудь одну из всех прямых.

Часто в задаче удаленность точки от прямой измеряют не расстоянием, а разностью ординат $ k,x_i+b-y_i $, и выбирают прямую так, чтобы сумма квадратов всех таких разностей была минимальна. Коэффициенты $ k_0 $ и $ b_ $ уравнения этой прямой дают некоторое решение стоящей перед нами задачи, которое отнюдь не является решением системы линейных уравнений $$ k,x_1+b=y_1,dots, k,x_+b=y_m $$ (вообще говоря, несовместной).

Рассмотрим теперь обобщение предложенной задачи. Пусть искомая зависимость между величинами $ y_ $ и $ x_ $ полиномиальная: $$ y_1=f(x_1),dots , y_m=f(x_m), quad npu quad f(x)=a_0+a_1x+dots+a_x^ $$ Величина $ varepsilon_i=f(x_i)-y_i $ называется $ i_ $-й невязкой 1) . Уравнения $$ left<begin a_0+a_1x_1+dots+a_x_1^&=&y_1, \ a_0+a_1x_2+dots+a_x_2^&=&y_2, \ dots & & dots \ a_0+a_1x_m+dots+a_x_m^&=&y_m end right. $$ называются условными. Матрица этой системы — матрица Вандермонда (она не обязательно квадратная).

Предположим что данные интерполяционной таблицы $$ begin x & x_1 & x_2 & dots & x_m \ hline y & y_1 & y_2 &dots & y_m end $$ не являются достоверными: величины $ x_ $ нам известны практически без искажений (т.е. на входе процесса мы имеем абсолютно достоверные данные), а вот измерения величины $ y_ $ подвержены случайным (несистематическим) погрешностям.

Задача. Построить полином $ f_(x) $ такой, чтобы величина $$ sum_^m [f(x_j)-y_j]^2 $$ стала минимальной. Решение задачи в такой постановке известно как метод наименьшик квадратов 2) .

В случае $ deg f_ =m-1 $ мы возвращаемся к задаче интерполяции в ее классической постановке. Практический интерес, однако, представляет случай $ deg f_ n $: $$S=left(begin 1 &1&1&ldots&1\ x_1 &x_2&x_3&ldots&x_\ vdots&& & &vdots\ x_1^ &x_2^&x_3^&ldots&x_m^ endright) cdot left(begin 1 &x_1&x_1^2&ldots&x_1^\ 1 &x_2&x_2^2&ldots&x_2^\ ldots&& & &ldots\ 1 &x_m&x_m^2&ldots&x_m^ endright)$$ $$det S = sum_<1le j_1 0 $. По теореме Крамера система нормальных уравнений имеет единственное решение.

Осталось недоказанным утверждение, что полученное решение доставляет именно минимум сумме квадратов невязок. Этот факт следует из доказательства более общего утверждения — о псевдорешении системы линейных уравнений. Этот результат приводится ☟ НИЖЕ. ♦

Собственно минимальное значение величины cуммы квадратов невязок, а точнее усреднение по количеству узлов $$ sigma=fracsum_^m (f(x_j) -y_j)^2 $$ называется среднеквадратичным отклонением.

Показать, что линейный полином $ y=a_+a_1x $, построенный по методу наименьших квадратов, определяет на плоскости $ (x_,y) $ прямую, проходящую через центроид

Пример. По методу наименьших квадратов построить уравнение прямой, аппроксимирующей множество точек плоскости, заданных координатами из таблицы

$$ begin x & 0.5 & 1 & 1.5 & 2 & 2.5 & 3 \ hline y & 0.35 & 0.80 & 1.70 & 1.85 & 3.51 & 1.02 end $$

Решение. Имеем $$ s_0=6, s_1=0.5 + 1 + 1.5 + 2 + 2.5 + 3=10.5, $$ $$ s_2=0.5^2 + 1^2 + 1.5^2 + 2^2 + 2.5^2 + 3^2=22.75, $$ $$t_0=0.35 + 0.80 + 1.70 + 1.85 + 3.51 + 1.02=9.23, $$ $$ t_1 =0.5cdot 0.35 + 1 cdot 0.80 + 1.5 cdot 1.70 + 2 cdot 1.85 + $$ $$ +2.5 cdot 3.51 + 3 cdot 1.02=19.06 . $$ Решаем систему нормальных уравнений $$ left( begin 6 & 10.5 \ 10.5 & 22.75 end right) left( begin a_0 \ a_1 end right)= left( begin 9.23 \ 19.06 end right), $$ 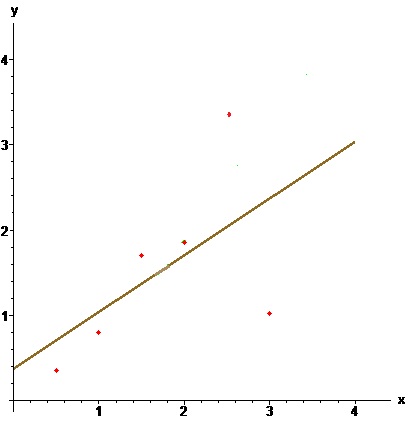получаем уравнение прямой в виде $$ y= 0.375 + 0.665, x .$$

Вычислим и полиномы более высоких степеней. $$ f_2(x)=-1.568+3.579, x-0.833,x^2 , $$ $$ f_3(x)=2.217-5.942,x+5.475,x^2-1.201, x^3 , $$ $$ f_4(x)= -4.473+17.101,x-19.320,x^2+9.205, x^3-1.487,x^4 , $$ $$ f_5(x)= 16.390-71.235,x+111.233,x^2-77.620,x^3+25.067,x^4-3.0347, x^5 . $$

Среднеквадратичные отклонения: $$ begin deg & 1 & 2 & 3 & 4 & 5 \ hline sigma & 0.717 & 0.448 & 0.204 &0.086 & 0 end $$ ♦

Возникает естественный вопрос: полином какой степени следует разыскивать в МНК? При увеличении степени точность приближения, очевидно, увеличивается. Вместе с тем, увеличивается сложность решения системы нормальных уравнений и даже при небольших степенях $ n $ (меньших $ 10 $) мы столкнемся с проблемой чувствительности решения к точности представления входных данных.

Видео:Неоднородная система линейных уравненийСкачать

Влияние систематических ошибок

Пример. Уравнение прямой, аппроксимирующей множество точек плоскости, заданных координатами из таблицы

$$ begin x & 0.5 & 1 & 1.5 & 2 & 2.5 & 3 \ hline y & 0.35 & 0.80 & 1.70 & 1.85 & 2.51 & 2.02 end $$ имеет вид (охра) $$ y=0.175+0.779, x , . $$ Теперь заменим значение $ y_5 $ на $ 0.2 $. Уравнение прямой принимает вид: $$ y=0.483+0.383, x , . $$ График (зеленый) существенно изменился. Почему это произошло? — Дело в том, что эффективность метода наименьших квадратов зависит от нескольких предположений относительно входных данных: в нашем случае — значений $ y $. Предполагается, что эти величины являлись результатами экспериментов, измерений, и, если они подвержены погрешностям, то эти погрешности носят характер несистематических флуктуаций вокруг истинных значений. Иными словами, изначально предполагается, что в действительности точки плоскости должны лежать на некоторой прямой. И только несовершенство наших методов измерений (наблюдений) демонстрирует смещение их с этой прямой. Ответ для исходной таблицы визуально подтвержает это предположение: экспериментальные точки концентрируются вокруг полученной прямой и величины невязок (отклонений по $ y $-координате) имеют «паритет» по знакам: примерно половина точек лежит выше прямой, а половина — ниже.

После замены значения $ y_5 $ на новое, значительно отличающееся от исходного, существенно меняется величина $ 5 $-й невязки $ varepsilon_5= ax_5+b-y_5 $. А поскольку в минимизируемую функцию эта невязка входи еще и в квадрате, то понятно, что изначальная прямая просто не в состоянии правильно приблизить новую точку.

Эта проблема становится актуальной в тех случаях, когда в «истинно случайный» процесс привносятся намеренные коррективы. Данные начинают подвергаться существенным искажениям, возможно, даже имеющим «злой» умысел 3) .

Как бороться с ошибками такого типа? Понятно, что решение возможно в предположении, что число таких — систематических — ошибок должно быть существенно меньшим общего количества экспериментальных данных. Понятно, что каким-то образом эти «выбросы» надо будет исключить из рассмотрения, т.е. очистить «сырые» данные от «мусора» — прежде чем подсовывать их в метод наименьших квадратов (см. ☞ цитату). Как это сделать?

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Псевдорешение системы линейных уравнений

Рассмотрим теперь обобщение задачи предыдущего пункта. В практических задачах часто бывает нужно найти решение, удовлетворяющее большому числу возможно противоречивых требований. Если такая задача сводится к системе линейных уравнений $$ left<begin a_x_1 +a_x_2+ldots+a_x_n &=&b_1\ a_x_1 +a_x_2+ldots+a_x_n &=&b_2\ ldots& & ldots \ a_x_1 +a_x_2+ldots+a_x_n &=&b_m endright. iff AX= $$ при числе уравнений $ m_ $ большем числа неизвестных $ n_ $, то такая переопределенная система, как правило, несовместна. В этом случае задача может быть решена только путем выбора некоторого компромисса — все требования могут быть удовлетворены не полностью, а лишь до некоторой степени.

Псевдорешением системы $ AX= $ называется столбец $ Xin mathbb R^n $, обеспечивающий минимум величины $$ sum_^m [a_x_1 +a_x_2+ldots+a_x_n-b_i]^2 . $$

Теорема. Существует псевдорешение системы

$$ AX= $$ и оно является решением системы $$ left[A^A right]X=A^ . $$ Это решение будет единственным тогда и только тогда, когда $ operatorname A =n $.

Система $ left[A^A right]X=A^ $ называется нормальной системой по отношению к системе $ AX= $. Формально она получается домножением системы $ AX= $ слева на матрицу $ A^ $. Заметим также, что если $ m=n_ $ и $ det A ne 0 $, то псевдорешение системы совпадает с решением в традиционном смысле.

Доказательство ☞ ЗДЕСЬ.

Если нормальная система имеет бесконечное количество решений, то обычно в качестве псевдорешения берут какое-то одно из них — как правило то, у которого минимальна сумма квадратов компонент («длина»).

Пример. Найти псевдорешение системы

$$x_1+x_2 = 2, x_1-x_2 = 0, 2, x_1+x_2 = 2 .$$

Решение. Имеем: $$A=left( begin 1 & 1 \ 1 & -1 \ 2 & 1 end right), operatorname A =2, = left( begin 2 \ 0 \ 2 end right), A^A= left( begin 6 & 2 \ 2 & 3 end right), A^ = left( begin 6 \ 4 end right). $$

Ответ. $ x_1=5/7, x_2 = 6/7 $.

Показать, что матрица $ A^A $ всегда симметрична.

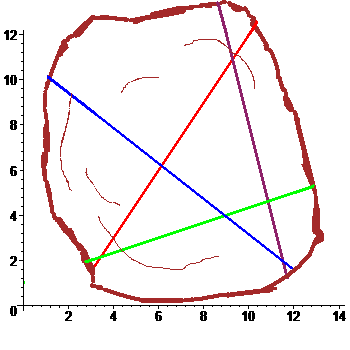
На дубовой колоде лежит мелкая монетка. К колоде

по очереди подходят четыре рыцаря и каждый наносит удар мечом, стараясь попасть по монетке. Все промахиваются. Расстроенные, рыцари уходят в харчевню пропивать злосчастную монетку. Укажите максимально правдоподобное ее расположение, имея перед глазами зарубки: $$ begin 3, x &- 2, y&=& 6,\ x &-3,y&=&-3,\ 11,x& + 14,y&=& 154, \ 4,x&+y&=&48. end $$

Видео:Псевдорешение переопределенных систем. ТемаСкачать

Геометрическая интерпретация

Видео:Базисные решения систем линейных уравнений (03)Скачать

Псевдообратная матрица

Пусть сначала матрица $ A_ $ порядка $ mtimes n_ $ — вещественная и $ m ge n_ $ (число строк не меньше числа столбцов). Если $ operatorname (A) = n $ (столбцы матрицы линейно независимы), то псевдообратная к матрице $ A_ $ определяется как матрица $$ A^=(A^A)^ A^ . $$ Эта матрица имеет порядок $ n times m_ $. Матрица $ (A^A)^ $ существует ввиду того факта, что при условии $ operatorname (A) = n $ будет выполнено $ det (A^ A) > 0 $ (см. упражнение в пункте ☞ ТЕОРЕМА БИНЕ-КОШИ или же пункт ☞ СВОЙСТВА ОПРЕДЕЛИТЕЛЯ ГРАМА ). Очевидно, что $ A^ cdot A = E_ $, т.е. псевдообратная матрица является левой обратной для матрицы $ A_ $. В случае $ m=n_ $ псевдообратная матрица совпадает с обратной матрицей: $ A^=A^ $.

Пример. Найти псевдообратную матрицу к матрице $$ A= left( begin 1 & 0 \ 0 & 1 \ 1 & 1 end right) . $$

Решение. $$ A^= left( begin 1 & 0 & 1 \ 0 & 1 & 1 end right) Rightarrow A^ cdot A = left( begin 2 & 1 \ 1 & 2 end right) Rightarrow $$ $$ Rightarrow (A^ cdot A)^ = left( begin 2/3 & -1/3 \ -1/3 & 2/3 end right) Rightarrow $$ $$ Rightarrow quad A^ = (A^ cdot A)^ A^ = left( begin 2/3 & -1/3 & 1/3 \ -1/3 & 2/3 & 1/3 end right) . $$ При этом $$ A^ cdot A = left( begin 1 & 0 \ 0 & 1 end right),quad A cdot A^ = left( begin 2/3 & -1/3 & 1/3 \ -1/3 & 2/3 & 1/3 \ 1/3 & 1/3 & 2/3 end right) , $$ т.е. матрица $ A^ $ не будет правой обратной для матрицы $ A_ $. ♦

Вычислить псевдообратную матрицу для $$ mathbf left( begin 1 & 0 \ 1 & 1 \ 1 & 1 end right) quad ; quad mathbf left( begin x_1 \ x_2 \ x_3 end right) . $$

Концепция псевдообратной матрицы естественным образом возникает из понятия псевдорешения системы линейных уравнений . Если $ A^ $ существует, то псевдорешение (как правило, переопределенной и несовместной!) системы уравнений $ AX=mathcal B_ $ находится по формуле $ X= A^ mathcal B $ при любом столбце $ mathcal B_ $. Верно и обратное: если $ E_, E_,dots, E_ $ – столбцы единичной матрицы $ E_m $: $$ E_=left( begin 1 \ 0 \ 0 \ vdots \ 0 end right), E_=left( begin 0 \ 1 \ 0 \ vdots \ 0 end right),dots, E_=left( begin 0 \ 0 \ 0 \ vdots \ 1 end right), $$ а псевдорешение системы уравнений $ AX=E_ $ обозначить $ X_ $ (оно существует и единственно при условии $ operatorname (A) = n $), то $$ A^=left[X_1,X_2,dots,X_m right] . $$

Теорема. Пусть $ A_ $ вещественная матрица порядка $ mtimes n_ $, $ m ge n_ $ и $ operatorname (A) = n $. Тогда псевдообратная матрица $ A^ $ является решением задачи минимизации

$$ min_<Xin mathbb R^> |AX-E_m|^2 $$ где минимум разыскивается по всем вещественным матрицам $ X_ $ порядка $ ntimes m_ $, а $ || cdot || $ означает евклидову норму матрицы (норму Фробениуса) : $$ |[h_]_|^2=sum_ h_^2 . $$ При сделанных предположениях решение задачи единственно.

С учетом этого результата понятно как распространить понятие псевдообратной матрицы на случай вещественной матрицы $ A_^ $, у которой число строк меньше числа столбцов: $ m ☞ ЗДЕСЬ

Видео:Фундаментальная система решений системы линейных уравнений ФСР СЛАУСкачать

Источники

[1]. Беклемишев Д.В. Дополнительные главы линейной алгебры. М.Наука.1983, с.187-234

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Псевдорешения системы линейных уравнений

Как показано выше, система линейных алгебраических уравнений с неизвестными

может иметь единственное решение, бесконечно много решений или вообще не иметь решений. Все эти случаи встречаются на практике. В частности, несовместной системе отвечает противоречивая ситуация, сложившаяся при математическом описании реальных объектов или процессов. Разумеется, что несовместная система не имеет решения в привычном понимании. Поэтому возникает необходимость изменить само понятие решения так, чтобы любая система линейных уравнений имела бы единственное в некотором смысле «решение».

Для дальнейших рассуждений нам потребуется количественная характеристика для «измерения» и «сравнения» между собой матриц-столбцов. Для этого каждому столбцу поставим в соответствие неотрицательное действительное число.

Модулем (нормой) столбца называется неотрицательное число

Заметим, что величина характеризует погрешность решения системы. Если величина велика, то столбец — плохое приближенное решение. Если погрешность мала, то столбец — хорошее приближенное решение. Если же является решением системы (в привычном понимании), то .

Псевдорешением системы линейных уравнений (5.27) называется наименьший по модулю столбец среди всех столбцов , минимизирующих величину .

Любая система имеет единственное псевдорешение

где матрица — псевдообратная для матрицы системы.

Понятие псевдорешения позволяет обойти не только факт неединственности, но и факт несуществования решений. Если система несовместна, то псевдорешение обеспечивает наименьшую величину погрешности . Если система совместна, то псевдорешение является ее решением, т.е. , причем наименьшим по модулю.

Видео:Общее, частное, базисное решение системы линейных уравнений Метод ГауссаСкачать

Алгоритм нахождения псевдорешения неоднородной системы

1. Найти псевдообратную матрицу одним из способов, рассмотренных ранее.

2. Найти псевдорешение .

Пример 5.8. Найти псевдорешение системы уравнений

Решение. 1. Найдем псевдообратную матрицу. При решении примера 5.6 матрица системы была приведена к простейшему виду

По матрицам и находим псевдообратную матрицу. Вычисляем произведения и разбиваем их на блоки

По формуле (4.21) вычисляем псевдообратную матрицу

2. Находим псевдорешение

Покажем, что это решение минимальное по модулю по сравнению со вееми остальными решениями системы. Действительно, в примере 5.5 было найдено общее решение рассматриваемой системы

Модуль этого столбца имеет выражение

Вместо минимизации модуля будем искать минимум его квадрата, чтобы избавиться от квадратного корня. Эти задачи, разумеется, эквивалентны, так как точки минимума неотрицательной функции и ее квадрата совпадают. Итак, будем искать минимум функции

зависящей от двух переменных.

Для нахождения стационарных точек приравниваем частные производные первого порядка нулю (применяем необходимое условие экстремума):

Упрощая уравнения, получаем систему которую решаем, например, по правилу Крамера:

Поскольку угловые миноры матрицы Гессе положительные: 0,» png;base64,iVBORw0KGgoAAAANSUhEUgAAAHIAAAAUBAMAAACjXnQJAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAgUEBwBDoZach0DFRkT91eccAAAG6SURBVDjLY2CgBLBuIFcnx0vs4hMYWAMYmLUN0MUnBcBY815g1cj8ysNtAnOVSA6aeIRjLozZ8W4CVp3v3nky8GQyrFNAFW9hCBOAejO1rwGrzkWaDAyMLxjugdQxHoYJcz5nYHwMYTIK6GH1KLMzkOD2YfArABkvVQwVZn/EwPgGwgwLYHmBXacSKChY08ABwipVChG2fcTA9BDCFGRgQvLoJiUQ0ATpTBFMB1pa5Q31VJUomGaB62RNZWDwA3kUEquFgiAgDdKZylCnwMAu4QRzQ9VNVJ2MwADQS2XglHLAdLAeyMS+ArjWVhSdYUBvsDxkYJ3ogJm07JKB9LlkmE4VkE6ORwzsEJ0SQMz0LICBEaLzINy1XK+BOnlbGfSgccBc1gl2IzBsn4P5mcYGxsZ+AjCdiBAyyQS6Nu4NzE5maAhxA+PzJcMcYPSkuABBXipMJwIAA6BvA9dSqD9ZxUSh4h4MbA3MeQUMbO/A4CGmTuYWkSQG7hUSiSjRycAQ1e4SwAB0JLMxBGDqZLA+BMwmRkXguOYtRogfBMYfkwCS4xxIyZnmB+BMbreUAhJ0RhmQWRgwVzMAAOFba2RqKNaHAAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAALoAAAAXBAMAAABOokjyAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAgb0BQZwQIVnQ8DHgccy0xpgAAAKxSURBVEjH1ZTPaxNBFMdf9mfCRkgCIlKQdEOrQQlLVrBKCS0NehDCUgwYDWXxog1SgkcP0mqFNodStQh6EDGQFE8R9OhFpQhCyU0UFJI0mFqzf4Nvdjeb/dWL0kOHMJudmffZ9+M7D+AwjOljBwgPfv3eODg6FQ/F99ni/v+zgQi1H5395b9eBk4F+rI0XOEves/g6iWcShHXDp01DO91feH0rvi8DN9im0N4srDojPo+MrliAee827yS/6I/81rZl65pJyFYhxdTg5W7kcknjiPJFHLnFaoDE4rLmt+Eih5YLaX40jcw4kAbTlgxP5NK684zOdy7pk5W4SE0yfs7y0/2JWQIlo3kfBNPJ3ASTkGqaS4wLeAkD51vA60Ko1HdQ2ZsgA8n4DwJ9LZKdf3pWZXk9rU6cKe35L4zSA+2pkeAFUWjIow4Y+xkEpDu4DMKjC3xb7NkEBXQH6JYUGH1tCXqrufOID2we/0nIZtR8bMGPhfX6dwWACnOLUNtS1EyRgi9BmtTEDy6QZZvEnobQh+99D8SW7eXs/jApFM75CLg3xrwV854lEPjEaDn0DN6G51O93UDeKM70BjQuxDoO9RyfNGk75G0o1ctYBX3XcYrnKmSc1WTjmiq76W3yM9up9MXjLxHSS1+q+w6G3dmJryHdHYcch0zMwGT7szMhIvOF/TMXEgACpXbkiVZJokPKc6qpusY3kIP1qqmnYCZcWk3pwCHmenZ4LOLsi4BXe9HXok4tmsAq6q7M8FcI/R0qHcQpZLiLowERZUa3mDGlAwwO0QTYU0ffRDG3UUVY5+AF2PDsOdHHzs9SGlaB248Slp6YMastlH58Rk/LxsD7qhNF11YRg2fXbZJacXdq2mShfcz1vuwE9DnVmyG3NWsf4eW/7Xny7auQWmaAodr/AUkDbKlexLEIQAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />, то найденная стационарная точка является точкой минимума.

Следовательно, наименьший модуль среди всех решений системы имеет решение

что совпадает с ранее найденным псевдорешением.

Пример 5.9. Найти псевдорешение системы линейный уравнений

Решение. Нетрудно заметить, что эта система несовместна (сложив второе и третье уравнения, получим уравнение , которое противоречит первому уравнению системы). Составим матрицу системы

Псевдообратная матрица для матрицы была найдена в примере

2. По формуле (5.28) получаем псевдорешение

Покажем, что это решение минимизирует погрешность . Для этого найдем минимум квадрата этой функции (см. пример 5.8)

2. Приравнивая к нулю частные производные по переменным , получаем после упрощений систему уравнений

Методом Гаусса находим общее решение этой системы (5.29)

где — свободная переменная. Следовательно, функция имеет бесконечно много стационарных точек, на которых достигается ее наименьшее значение. Заметим, что найденное псевдорешение принадлежит этому множеству. Покажем теперь, что — это наименьший по модулю элемент множества (5.29). Для этого составим функцию, равную квадрату модуля решения

Найдем точку минимума этой функции одной переменной:

Поскольку функция выпуклая, наименьшее по модулю решение (5.29) получается при . Это решение совпадает с найденным ранее псевдорешением .