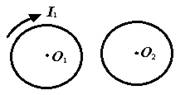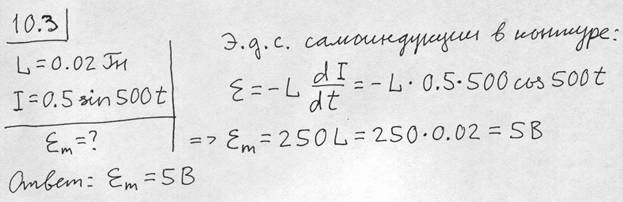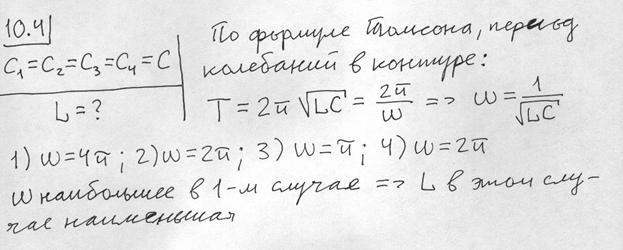Ниже приведены уравнения собственных незатухающих колебаний (5 видео)

Ниже приведены уравнения собственных незатухающих колебаний

незатухающие гармонические колебания

Активное сопротивление колебательного контура R = 0,4 Ом. Определите среднюю мощность

, потребляемую колебательным контуром, при поддержании в нем незатухающих гармонических колебаний с амплитудным значением силы тока I_m = 30 мА.

Ниже приведены уравнения собственных незатухающих электромагнитных колебаний в четырех контурах с одинаковой емкостью. Индуктивность L контура наименьшая в случае, приведенном под номером
1) q = 10 –6 cos(4πt + π/4), Кл
2) U = 3cos2πt, В
3) q = 10 –8 cos(πt + π/6), Кл
4) I = –2·sin2πt, А

Источник незатухающих гармонических колебаний движется по закону S = 5sin314t. Определить смещение от положения равновесия, скорость и ускорение точки, находящейся на расстоянии 340 м от источника через одну секунду после начала колебаний, если скорость распространения волн u = 340 м/с.

При незатухающих гармонических колебаниях точки ее максимальная скорость равна 0,1 м/с, а максимальное ускорение равно 1 м/с 2 . Написать уравнение колебаний, считая, что в начальный момент времени смещение максимально.

Источник незатухающих гармонических колебаний движется по закону s₀ = 5sin3140t. Определить смещение от положения равновесия, скорость и ускорение точки через 1 с, находящейся на расстоянии 340 м от источника, если скорость распространения волн v = 340 м/с после начала колебания.

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Ниже приведены уравнения собственных незатухающих колебаний

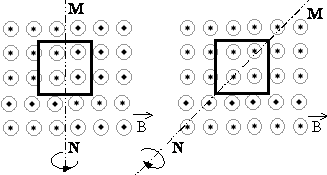
10.1. На рисунке показаны два способа вращения проволочной рамки в однородном магнитном поле, линии индукции которого идут из плоскости чертежа. Вращение происходит вокруг оси MN . Ток в рамке

1) Существует в обоих случаях

2) Не существует ни в одном из случаев

3) Существует только в первом случае

4) Существует только во втором случае

10.2. На рисунке изображены расположенные в плоскости чертежа витки 1 и 2. По витку 1 течет убывающий со временем ток I₁. Как направлено поле индукционного тока I₂, возникающего во втором витке в точке О₂?

10.3 Через контур, индуктивность которого L = 0,02 Гн, течет ток, изменяющийся по закону I = 0,5 sin 500 t . Найдите амплитудное значение ЭДС самоиндукции, возникающей в контуре.

10.4. Ниже приведены уравнения собственных незатухающих электромагнитных колебаний в четырех контурах с одинаковой емкостью. Индуктивность L контура наименьшая в случае, приведенном под номером …

1) q =10 -6 cos (4 p t + 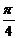), Кл 2) U =3 cos 2 p t , В

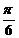
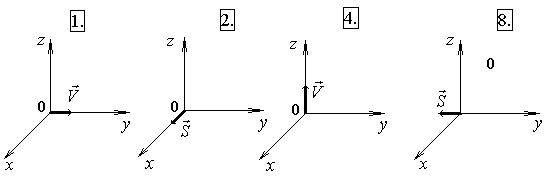
3) q=10 -8 cos( p t + ), Кл 4) I= -2 × sin2 p t , А

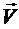
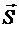
10.5. Ниже стрелками указаны векторы скорости и векторы Умова-Пойнтинга плоской электромагнитной волны.

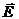
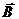
В каких случаях векторы и волны расположены в плоскости х0 z ? Укажите сумму номеров этих диаграмм.

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Дисциплина: Физика тема: 060 Механические колебания и волны (стр. 5 )

Ниже приведены уравнения собственных незатухающих колебаний

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14

4) Знак неопределим

17. [Уд1] (ВО1) Направления индукционного тока в контуре и магнитного поля (к нам) указывают, что для величины магнитной индукции справедливо соотношение

4) Знак неопределим

18. [Уд1] (О) При движении рамок в однородном магнитном поле в направлениях, указанных стрелками, ЭДС индукции возникает в случае под номером

19. [Уд1] (О) По параллельным металлическим проводникам, расположенным в однородном магнитном поле, с постоянной скоростью перемещается перемычка. Зависимость Ei — ЭДС индукции, возникающей в цепи, правильно представлена на рисунке под номером

Тема: 250 Электромагнитные колебания и волны

V251П Электромагнитные колебания.

S251 П электромагнитные колебания – 23 задания

1. [Уд] (ВО1) В колебательном контуре зависимость заряда на пластинах конденсатора от времени описывается дифференциальным уравнением вида . Эти колебания называются

2. [Уд] (ВО1) В колебательном контуре зависимость заряда на пластинах конденсатора от времени описывается дифференциальным уравнением вида . Эти колебания называются

3. [Уд] (ВО1) В колебательном контуре зависимость заряда на пластинах конденсатора от времени описывается дифференциальным уравнением вида . Эти колебания называются

4. [Уд] (ВО1). Если частота колебаний в контуре возросла в 3 раза, а заряд конденсатора и индуктивность катушки не менялись, то энергия магнитного поля в катушке … раз(а).

1) уменьшилась в 3

2) увеличилась в 3

3) уменьшилась в 9

4) увеличилась в 9

5. [Уд] (ВО1) Максимальная энергия электрического колебательного контура 4,5 Дж. При циклической частоте свободных колебаний в контуре, равной 1·104с-1, и емкости конденсатора 4 мкФ максимальный ток через катушку индуктивности равен

6. [Уд] (ВО1) В колебательном контуре в начальный момент времени напряжение на конденсаторе максимально. Напряжение на конденсаторе станет равным нулю через долю периода электромагнитных колебаний, равную

7. [Уд] (ВО1) В колебательном контуре в начальный момент времени напряжение на конденсаторе максимально. Сила тока станет равной нулю через долю периода электромагнитных колебаний, равную

8. [Уд] (ВО1) Сила тока в колебательном контуре изменяется по закону ,мА. Амплитуда колебаний заряда на обкладках конденсатора равна … мкКл.

9. [Уд] (ВО1) Если в колебательном контуре увеличить емкость конденсатора в 2 раза и заряд на нем увеличить в 2 раза, то амплитуда колебаний тока в контуре … раз(а).

1) увеличится в 2

2) увеличится в

3) уменьшится в

4) уменьшится в 2

10. [Уд] (ВО1) Если в колебательном контуре уменьшить емкость конденсатора в 2 раза, то, при одинаковом заряде конденсатора, максимальная энергия магнитного поля в катушке индуктивности … раза.

1) увеличится в 2

2) увеличится в

3) уменьшится в

4) уменьшится в 2

11. [Уд] (ВО1) Если частота колебаний в контуре возросла в 2 раза, а заряд конденсатора и индуктивность катушки не менялись, то энергия магнитного поля в катушке … раза.

1) уменьшилась в 2

2) увеличилась в 2

3) уменьшилась в 4

4) увеличилась в 4

12. [Уд] (ВО1) Время релаксации затухающих электромагнитных колебаний наибольшее в случае

1) , мкКл

2) , мкКл

3) , В

4) , В

13. [Уд] (ВО1) Ниже приведены уравнения затухающих электромагнитных колебаний. Логарифмический декремент затухания наибольший в случае

1) , В

2), мкКл

3) , мкКл

4) , В

14. [Уд] (ВО1) Уменьшение амплитуды колебаний в системе с затуханием характеризуется временем релаксации. Если при неизменном омическом сопротивлении в колебательном контуре увеличить в 2 раза индуктивность катушки, то время релаксации … раза.

1) уменьшится в 4

2) увеличится в 2

3) увеличится в 4

4) уменьшится в 2

15. [Уд] (ВО1) Уменьшение амплитуды колебаний в системе с затуханием характеризуется временем релаксации. Если при неизменной индуктивности в колебательном контуре увеличить омическое сопротивление в 2 раза катушки, то время релаксации … раза.

1) уменьшится в 4

2) увеличится в 2

3) увеличится в 4

4) уменьшится в 2

16. [Уд] (ВО1) Ниже приведены уравнения собственных незатухающих электромагнитных колебаний в четырех контурах с одинаковой емкостью. Индуктивность L контура наименьшая в случае

1) q = 10-6cos(4πt +), Кл

3) q = 10-8cos(πt +), Кл

17. [Уд] (ВО1) Ниже приведены уравнения собственных незатухающих электромагнитных колебаний в четырех контурах с одинаковой индуктивностью. Емкость C контура наибольшая в случае

1) q = 10-6cos(4πt +), Кл

3) q = 10-8cos(πt +), Кл

18. [Уд] (ВО1) Уравнение изменения тока со временем в колебательном контуре имеет вид А. Индуктивность контура L =1 Гн. Емкость контура C равна … нФ.

19. [Уд] (ВО1) Уравнение изменения тока со временем в колебательном контуре имеет вид А. Если индуктивность контура составляет L =1 Гн, то максимальное напряжение между обкладками равно … В.

20. [Уд] (ВО1) Уравнение изменения тока со временем в колебательном контуре имеет вид А. Индуктивность контура L =1 Гн. Максимальная энергия электрического поля составляет … мДж.